声场中球形空化云中气泡的耦合谐振

张鹏利; 林书玉; 朱华泽; 张涛

doi:10.7498/aps.68.20190360

摘要

本文从泡群中气泡动力学方程出发, 对泡壁运动方程进行线性约化, 得到球状泡群中气泡谐振频率的表达式, 并给出了泡群中气泡谐振频率与单泡Minnaert频率的修正系数. 讨论了泡群中气泡初始半径、气泡数量、气泡之间距离对谐振频率的影响. 研究结果表明: 考虑到气泡的相互作用后, 球状泡群中气泡的谐振频率明显小于单泡的Minnaert频率. 随着泡群中气泡数量的减少、气泡之间距离增大, 泡群中气泡之间的相互作用减弱, 气泡的谐振频率回归到Minnaert单泡谐振频率. 同时泡群中气泡的谐振频率随气泡之间距离、气泡数量的影响变化梯度也不相同. 泡群中气泡数量越多、气泡距离近越近, 气泡之间相互作用强, 谐振频率变化幅度快.

关键词:

气泡 /
谐振频率 /
气泡数量 /
距离

Abstract

The interaction between bubbles in bubble group mainly acts on the other bubble through radiation sound pressure between the bubbles. In this paper, based on the bubble dynamics equation in bubble clouds, the equation of bubble wall motion is linearly reduced, the expression of bubble resonance frequency in spherical bubble group is obtained and the correction coefficient of bubble resonance frequency and single bubble are given. Furthermore, the effects of the initial radius, the number of bubbles and the distance between bubbles on the resonance frequency are discussed. The results show that the phase of bubbles is taken into account. Considering the interaction between bubbles, the resonance frequency of bubbles in spherical bubble group is obviously less than that of single bubble. With the decrease of the number of bubbles in bubble group, the distance between bubbles increases, the interaction between bubbles in bubble group decreases, and the resonance frequency of bubbles returns to the resonance frequency of Minnaert single bubble. At the same time, the resonance frequency of bubbles in bubble group changes gradient with the increase of the distance between bubbles and the number of bubbles. However, when the number of bubbles increases a certain value, the resonant frequency of the bubble is almost constant. When the bubble group has a certain radius, the more the number of bubbles, the smaller the resonance frequency of the bubble is, but there exists a critical value. It is also found that a smaller correction coefficient is held by the bubble group with larger initial radius, which indicates the same number of bubble groups. Under the same bubble spacing, the interaction of small bubbles with smaller bubbles is more significant, and the resonance frequency of the bubble is obviously affected. Because the frequency and amplitude of driving sound pressure can only be given values in ultrasonic cavitation, the resonant frequency of cavitation bubbles will be reduced by properly injecting air bubbles into liquid, which makes most of cavitation bubbles undergo intense non-linear oscillating steady-state cavitation. Therefore, the occurrence of cavitation can be effectively suppressed.

Keywords:

作者及机构信息

1.
陕西师范大学物理学与信息技术学院, 陕西省超声学重点实验室, 西安　710062

2.
西安科技大学理学院, 西安　710054

通信作者: 林书玉, 253383739@qq.com

基金项目: 国家自然科学基金(批准号: 50875132, 60573172)和陕西省科技厅工业攻关项目(批准号: 2015GY182, 2016GY-041)资助的课题.

Authors and contacts

1.
Institute of Applied Acoustics Shaanxi Normal University, Xi’an 710062, China

2.
College of Science, Xi’an University of Science and Technology, Xi’an 710054, China

Corresponding author: Lin Shu-Yu, 253383739@qq.com

Funds: Project supported by the National Natural Science Foundation of China (Grant Nos. 50875132, 60573172), and the Industrial Public Relation Project of Shaanxi Technology Committee, China (Grant Nos. 2015GY182, 2016GY-041).

文章全文 : translate this paragraph

参考文献

[1]	陈伟中 2014 声空化物理 (北京, 科学出版社)第2—5页 Chen W Z 2014 Sound Cavitation Physics (Beijing: Science Press) pp2–5 (in Chinese)
[2]	Rayleigh J W 1917 Philosophical Magazine 34 94
[3]	Cole R H 1948 Underwater Eplosion (Princeton: Princeton U.P)pp60–65
[4]	Npltingk B E 2002 Proc. Phys. Soc. 63 674
[5]	Plesset M S, Chapmam R B 1977 J. Fluid Mech. 9 145 Google Scholar
[6]	Mason T J, J P Lorimer 1988 Lorimer Application and Use of Ultrasound in Chemisty (USA: Ellis Horworrd Limited) pp130—135
[7]	Madrazo A, Garcia N, Nieto-Vesperinas M 1998 Phys. Rev. Lett. 80 4590 Google Scholar
[8]	Shim A 1971 J. Basic Engin. 93 426 Google Scholar
[9]	An Y 2011 Phys. Rev. E 83 66313−1 Google Scholar
[10]	王成会, 林书玉 2010 力学学报 42 1050 Wang C H, Lin S Y 2010 Acta Mech. Sin. 42 1050
[11]	胡静, 林书玉, 王成会, 李锦 2013 62 114334 Hu J, Lin S Y, Wang C H, Li J 2013 Acta Phys. Sin. 62 114334
[12]	王成会, 莫润阳, 胡静 2016 65 144301 Google Scholar Wang C H, Mo R Y, Hu J 2016 Acta Phys. Sin. 65 144301 Google Scholar
[13]	王成会, 程建春 2014 63 134301 Google Scholar Wang C H, Cheng J C 2014 Acta Phys. Sin. 63 134301 Google Scholar
[14]	Yasui K, Iida Y, Tuziuti T, et al. 2008 Phys. Rev. E 77 66313−1
[15]	Barber B P, Hiller R A, Ritva L, et al. 1997 Phys.Reports 281 65 Google Scholar
[16]	Kwak H Y, Na J H 1996 Phys. Rev. Lett. 77 4454 Google Scholar
[17]	Wang Q X 2004 Phys. Fluids 165 1610
[18]	Hsiao C T, Choi J K, Singh S, Chahine G L, et al 2013 J. Fluid Mech. 716 137 Google Scholar
[19]	Keith W, Seth J P 1996 Phys. Rev. E 54 R2205 Google Scholar
[20]	Cui P, Wang Q X, Wang S P, Zhang A M 2016 Phys. Fluids 28 94
[21]	苗博雅, 安宇 2015 64 204301−1 Google Scholar Miao B Y, An Y 2015 Acta Phys. Sin. 64 204301−1 Google Scholar
[22]	蔡军, 淮秀兰等 2015 科学通报 56 947 Cai J, Huai X L, et al. 2015 Chinese Sci Bull. 56 947
[23]	Wang C, Khoo B C, Yeo K S 2003 Comput. Fluids 32 1195 Google Scholar

施引文献

图 1 球形空化云中气泡的运动　(a)气泡初始半径5 μm; (b)泡群中气泡数量为100; (c), (d)气泡初始半径5 μm, 泡群中气泡数量N = 100

Fig. 1. Movement of bubbles in spherical cavitation clouds: (a) Bubble initial radius 5 μm; (b) the number 100; (c), (d) bubble initial radius 5 μm, N = 100.

下载: 全尺寸图片幻灯片

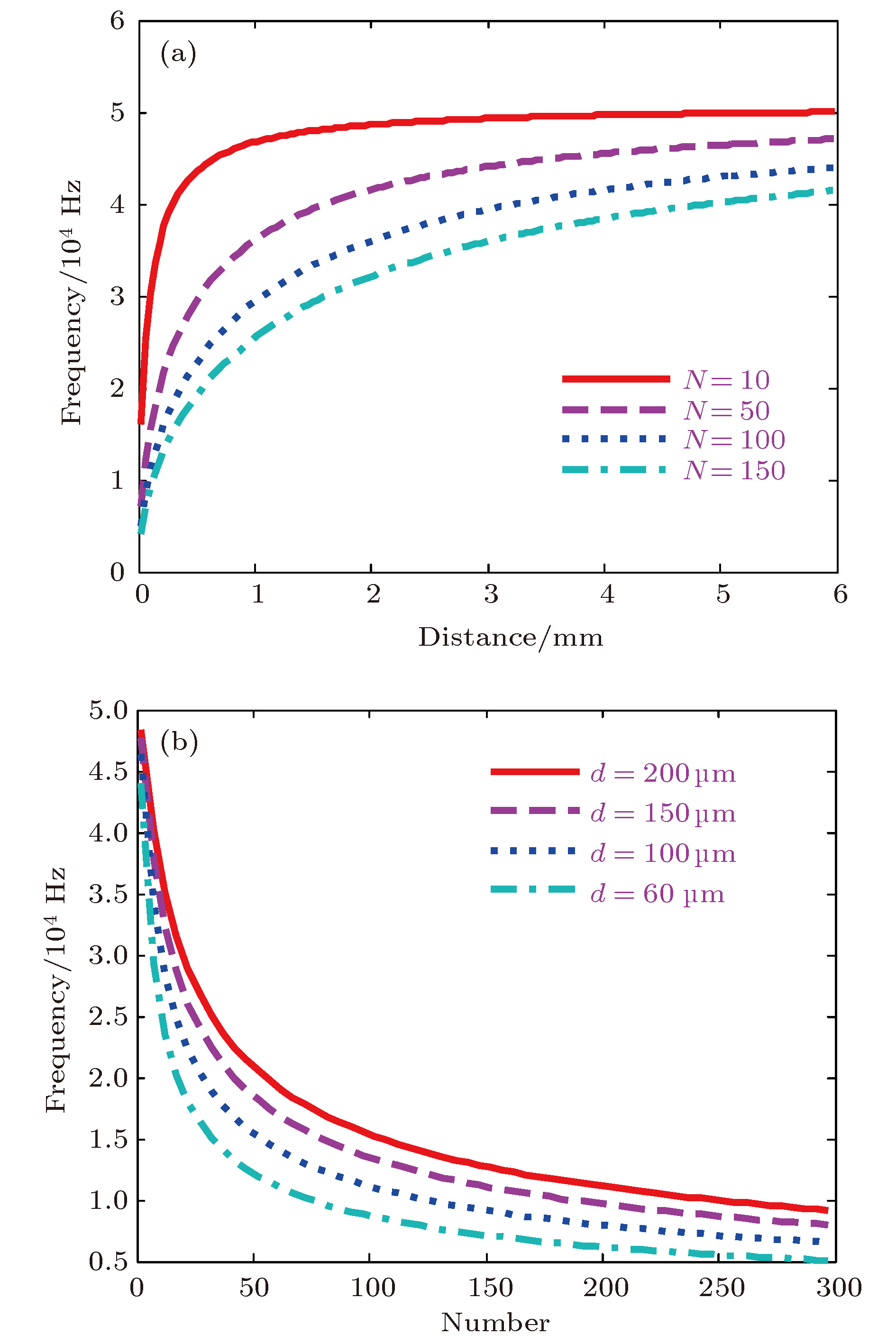
图 2 泡群中气泡的谐振频率　(a)气泡谐振频率与泡群中气泡之间距离关系; (b)气泡谐振频率与泡群中气泡数量之间关系, 气泡的初始半径均为20 μm

Fig. 2. Resonance frequency of bubbles in bubble group: (a) The relationship between bubble resonance frequency and distance in the bubble group; (b) the relationship between bubble resonance frequency and the number of bubbles in the bubble group, the initial radius of the bubbles is 20 μm.

下载: 全尺寸图片幻灯片

图 3 修正系数M与泡群中气泡距离关系

Fig. 3. Relationship between correction coefficient and bubble distance.

下载: 全尺寸图片幻灯片

图 4 气泡初始半径与泡群中气泡谐振频率的关系

Fig. 4. Relationship between the initial radius of bubbles and the resonant frequency of bubbles.

下载: 全尺寸图片幻灯片

图 5 单气泡体积变化图

Fig. 5. Volume change of single bubble

下载: 全尺寸图片幻灯片

图 7 球状气泡云体积变化图(N = 5)

Fig. 7. Volume change of spherical cavitation cloud N = 5.

下载: 全尺寸图片幻灯片

图 6 球状空化云气泡体积变化图(N = 9)

Fig. 6. Volume change of spherical cavitation cloud N = 9.

下载: 全尺寸图片幻灯片

map

[1]	陈伟中 2014 声空化物理 (北京, 科学出版社)第2—5页 Chen W Z 2014 Sound Cavitation Physics (Beijing: Science Press) pp2–5 (in Chinese)
[2]	Rayleigh J W 1917 Philosophical Magazine 34 94
[3]	Cole R H 1948 Underwater Eplosion (Princeton: Princeton U.P)pp60–65
[4]	Npltingk B E 2002 Proc. Phys. Soc. 63 674
[5]	Plesset M S, Chapmam R B 1977 J. Fluid Mech. 9 145 Google Scholar
[6]	Mason T J, J P Lorimer 1988 Lorimer Application and Use of Ultrasound in Chemisty (USA: Ellis Horworrd Limited) pp130—135
[7]	Madrazo A, Garcia N, Nieto-Vesperinas M 1998 Phys. Rev. Lett. 80 4590 Google Scholar
[8]	Shim A 1971 J. Basic Engin. 93 426 Google Scholar
[9]	An Y 2011 Phys. Rev. E 83 66313−1 Google Scholar
[10]	王成会, 林书玉 2010 力学学报 42 1050 Wang C H, Lin S Y 2010 Acta Mech. Sin. 42 1050
[11]	胡静, 林书玉, 王成会, 李锦 2013 62 114334 Hu J, Lin S Y, Wang C H, Li J 2013 Acta Phys. Sin. 62 114334
[12]	王成会, 莫润阳, 胡静 2016 65 144301 Google Scholar Wang C H, Mo R Y, Hu J 2016 Acta Phys. Sin. 65 144301 Google Scholar
[13]	王成会, 程建春 2014 63 134301 Google Scholar Wang C H, Cheng J C 2014 Acta Phys. Sin. 63 134301 Google Scholar
[14]	Yasui K, Iida Y, Tuziuti T, et al. 2008 Phys. Rev. E 77 66313−1
[15]	Barber B P, Hiller R A, Ritva L, et al. 1997 Phys.Reports 281 65 Google Scholar
[16]	Kwak H Y, Na J H 1996 Phys. Rev. Lett. 77 4454 Google Scholar
[17]	Wang Q X 2004 Phys. Fluids 165 1610
[18]	Hsiao C T, Choi J K, Singh S, Chahine G L, et al 2013 J. Fluid Mech. 716 137 Google Scholar
[19]	Keith W, Seth J P 1996 Phys. Rev. E 54 R2205 Google Scholar
[20]	Cui P, Wang Q X, Wang S P, Zhang A M 2016 Phys. Fluids 28 94
[21]	苗博雅, 安宇 2015 64 204301−1 Google Scholar Miao B Y, An Y 2015 Acta Phys. Sin. 64 204301−1 Google Scholar
[22]	蔡军, 淮秀兰等 2015 科学通报 56 947 Cai J, Huai X L, et al. 2015 Chinese Sci Bull. 56 947
[23]	Wang C, Khoo B C, Yeo K S 2003 Comput. Fluids 32 1195 Google Scholar

[1]	周少彤, 莫腾富, 任晓东, 徐强, 孙奇志, 张思群, 黄显宾, 张朝辉, 刘文燕. 水下电爆炸气泡脉动及能量特性实验研究. , 2024, 73(24): . doi: 10.7498/aps.73.20240720
[2]	赵昶, 纪献兵, 杨聿昊, 孟宇航, 徐进良, 彭家略. Janus颗粒撞击气泡的行为特征. , 2022, 71(21): 214701. doi: 10.7498/aps.71.20220632
[3]	张陶然, 莫润阳, 胡静, 陈时, 王成会, 郭建中. 弹性介质包围的球形液体腔中气泡和粒子的相互作用. , 2020, 69(23): 234301. doi: 10.7498/aps.69.20200764
[4]	王树山, 李梅, 马峰. 爆炸气泡与自由水面相互作用动力学研究. , 2014, 63(19): 194703. doi: 10.7498/aps.63.194703
[5]	史冬岩, 王志凯, 张阿漫. 相同尺度下气泡与复杂壁面的耦合特性研究. , 2014, 63(17): 174701. doi: 10.7498/aps.63.174701
[6]	李帅, 张阿漫. 上浮气泡在壁面处的弹跳特性研究. , 2014, 63(5): 054705. doi: 10.7498/aps.63.054705
[7]	刘云龙, 张阿漫, 王诗平, 田昭丽. 基于边界元法的近平板圆孔气泡动力学行为研究. , 2013, 62(14): 144703. doi: 10.7498/aps.62.144703
[8]	倪宝玉, 李帅, 张阿漫. 气泡在自由液面破碎后的射流断裂现象研究. , 2013, 62(12): 124704. doi: 10.7498/aps.62.124704
[9]	梁善勇, 王江安, 宗思光, 吴荣华, 马治国, 王晓宇, 王乐东. 基于多重散射强度和偏振特征的舰船尾流气泡激光探测方法. , 2013, 62(6): 060704. doi: 10.7498/aps.62.060704
[10]	李帅, 张阿漫, 王诗平. 气泡引起的皇冠型水冢实验与数值研究. , 2013, 62(19): 194703. doi: 10.7498/aps.62.194703
[11]	王诗平, 张阿漫, 刘云龙, 吴超. 圆形破口附近气泡动态特性实验研究. , 2013, 62(6): 064703. doi: 10.7498/aps.62.064703
[12]	张阿漫, 肖巍, 王诗平, 程潇欧. 不同沙粒底面下气泡脉动特性实验研究. , 2013, 62(1): 014703. doi: 10.7498/aps.62.014703
[13]	刘云龙, 张阿漫, 王诗平, 田昭丽. 基于边界元法的气泡同波浪相互作用研究. , 2012, 61(22): 224702. doi: 10.7498/aps.61.224702
[14]	吴伟, 孙东科, 戴挺, 朱鸣芳. 枝晶生长和气泡形成的数值模拟. , 2012, 61(15): 150501. doi: 10.7498/aps.61.150501
[15]	张阿漫, 王超, 王诗平, 程晓达. 气泡与自由液面相互作用的实验研究. , 2012, 61(8): 084701. doi: 10.7498/aps.61.084701
[16]	王诗平, 张阿漫, 刘云龙, 姚熊亮. 气泡与弹性膜的耦合效应数值模拟. , 2011, 60(5): 054702. doi: 10.7498/aps.60.054702
[17]	蒋丹, 李松晶, 包钢. 采用遗传算法对压力脉动过程中气泡模型参数的辨识. , 2008, 57(8): 5072-5080. doi: 10.7498/aps.57.5072
[18]	张阿漫, 姚熊亮. 近自由面水下爆炸气泡的运动规律研究. , 2008, 57(1): 339-353. doi: 10.7498/aps.57.339
[19]	张阿漫, 姚熊亮. 近壁面气泡的运动规律研究. , 2008, 57(3): 1662-1671. doi: 10.7498/aps.57.1662
[20]	张华伟, 李言祥. 金属熔体中气泡形核的理论分析. , 2007, 56(8): 4864-4871. doi: 10.7498/aps.56.4864

计量

文章访问数: 7863
PDF下载量: 123
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

声场中球形空化云中气泡的耦合谐振