-
在高Zeta势下, 研究平行板微通道中一类不可压缩微极性流体的时间周期电渗流. 在不使用Debye-Hückel线性近似条件下, 利用有限差分法数值求解非线性Poisson-Boltzmann方程和不可压缩微极性流体的连续性方程、动量方程、角动量方程及本构方程, 在低Zeta势下将所得结果与使用Debye-Hückel线性近似得到的解析解比较, 证明本文数值方法是可行的; 讨论高Zeta势下电动宽度m、电振荡频率
$ \varOmega $ 、微极性参数$ {k_1} $ 等无量纲参数对不可压缩微极性流体的速度和微旋转效应的影响. 研究表明: 1)随着Zeta势的增大, 微极性流体的速度、微旋转、体积流量、微旋强度以及剪切应力增大, 说明与低Zeta势相比, 高Zeta势对微极性流体电渗流有显著的促进作用. 2)在高Zeta势下, 随着微极性参数的增大, 微极性流体的速度减小, 但是对微旋转效应呈现先增强后减弱的趋势. 3)在高Zeta势下, 当电振荡频率较低(小于1)时, 电动宽度的增大促进微极性流体的流动, 但抑制其微旋转; 当电振荡频率较高(大于1)时, 电动宽度的增大抑制微极性流体的流动及微旋转, 但促进体积流量快速增大并趋于恒定. 4)在高Zeta势下, 当电振荡频率较低(小于1)时, 微极性流体电渗流速度和微旋转随着电振荡频率的变化呈现明显的振荡变化趋势, 但是速度和微旋转的峰值、体积流量及微旋强度均保持不变; 当电振荡频率较高(大于1)时, 随着电振荡频率的增大, 微极性流体电渗流速度和微旋转的幅值减小, 体积流量及微旋强度减小直至趋于零. 5)在高Zeta势下, 壁面剪切应力$ {\sigma _{21}} $ 及$ {\sigma _{12}} $ 的幅值随电动宽度的增大而增大; 当电振荡频率较低(小于1)时, 壁面剪切应力$ {\sigma _{21}} $ 与$ {\sigma _{12}} $ 不随电振荡频率的增大而变化, 均取恒定值, 且微极性参数的取值不影响壁面剪切应力$ {\sigma _{21}} $ 的幅值; 当电振荡频率较高(大于1)时, 壁面剪切应力$ {\sigma _{21}} $ 及$ {\sigma _{12}} $ 的幅值随电振荡频率的增大而减小, 且壁面剪切应力$ {\sigma _{21}} $ 的幅值随着微极性参数的增大而减小, 而壁面剪切应力$ {\sigma _{12}} $ 的振幅随着微极性参数的增大而线性减小.The time-periodic electroosmotic flow of a class of incompressible micropolar fluid in a parallel plate microchannel under high wall Zeta potential is studied in this work. Without using the Debye-Hückel linear approximation, the finite difference method is used to numerically solve the nonlinear Poisson-Boltzmann equation, the continuity equation, momentum equation, angular momentum equation, and constitutive equation of incompressible micropolar fluid. In the case of low Zeta potential, the results are compared with the analytical solution obtained in the Debye-Hückel linear approximation, and the feasibility of the numerical method is also proved. The influences of dimensionless parameters, such as electric width$ m $ , electric oscillation frequency$ \varOmega $ , and micro-polarity parameter$ {k_1} $ on the velocity and microrotation effect of incompressible micro-polarity fluid under high Zeta potential are discussed. The results are shown below. 1) With the increase of Zeta potential, the velocity, micro-rotation, volume flow, micro-rotation strength and shear stress of the micropolar fluid all increase, indicating that compared with the low Zeta potential, the high Zeta potential has a significant promotion effect on the electroosmotic flow of the micropolar fluid. 2) Under high Zeta potential, with the increase of the micro-polarity parameter, the velocity of the micropolar fluid decreases, and the micro-rotation effect shows a first-increasing-and-then-decreasing trend. 3) Under high Zeta potential, when the electric oscillation frequency is lower (less than 1), the increase of the electric width promotes the flow of the micropolar fluid, but impedes its micro-rotation; when the electric oscillation frequency is higher (greater than 1), the increase of the electric width impedes the flow and micro-rotation of the micropolar fluid, but expedites rapid increase of the volume flow rate and tends to be constant. 4) Under high Zeta potential, when the electric oscillation frequency is lower (less than 1), the electroosmotic flow velocity and micro-rotation of the micropolar fluid show an obvious oscillation trend with the change of the electric oscillation frequency, but the peak value of the velocity and micro-rotation, the volume flow rate and the micro-rotation intensity remain unchanged; when the electric oscillation frequency is higher (greater than 1), with the increase of the electric oscillation frequency, the amplitude of micropolar fluid electroosmotic flow velocity and the amplitude of microrotation decrease, and also the volume flow and microrotation intensity decrease until they reach zero. 5) Under high Zeta potential, the amplitude of wall shear stress$ {\sigma _{21}} $ and$ {\sigma _{12}} $ increase with the electric width increasing; when the electric oscillation frequency is lower (less than 1), the wall shear stress$ {\sigma _{21}} $ and$ {\sigma _{12}} $ do not change with the increase of the electric oscillation frequency, and the amplitude of the wall shear stress$ {\sigma _{21}} $ is not affected by the value of the micro-polarity parameter; when the electric oscillation frequency is higher (greater than 1), the amplitude of wall shear stress$ {\sigma _{21}} $ and$ {\sigma _{12}} $ decrease with the increase of the electric oscillation frequency, and the amplitude of wall shear stress$ {\sigma _{21}} $ decreases with the increase of the micro-polarity parameter, while the amplitude of wall shear stress$ {\sigma _{12}} $ decreases linearly with the increase of the micro-polarity parameter.-
Keywords:
- micropolar fluid /
- high Zeta potential /
- electroosmotic flow /
- parallel plate microchannel /
- finite difference method
[1] Osuga T, Sakamoto H, Takagi T 1996 J. Phys. Soc. Jpn. 65 1854
Google Scholar
[2] Polevoi V V, Bilova T E, Shevtsov Y I 2003 Biol. Bull 30 133
Google Scholar
[3] Dem'yanov A Y, Dinariev O Y, Sharaborin E L 2020 Russ. Phys. J. 63 113
Google Scholar
[4] Masuduzzaman M, Kim B H 2022 Langmuir 38 7244
Google Scholar
[5] Reuss F F 1809 Proc. Imp. Soc. Nat. Mos. 3 327
[6] Patankar N A, Hu H H 1998 Anal. Chem. 70 1870
Google Scholar
[7] Gleeson J P 2002 J. Colloid Interface Sci. 249 217
Google Scholar
[8] Fu L M, Lin J Y, Yang R J 2003 J. Colloid Interface Sci. 258 266
Google Scholar
[9] Stone H A, Stroock A D, Ajdari A 2004 Annu. Rev. Fluid Mech. 36 381
Google Scholar
[10] Park H M, Lee J S, Kim T W 2007 J. Colloid Interface Sci. 315 731
Google Scholar
[11] Jian Y J, Yang L G, Liu Q S 2010 Phys. Fluids 22 042001
Google Scholar
[12] Yoshida H 2016 Comput. Fluids 124 237
Google Scholar
[13] Nosrati R, Hadigol M, Raisee M 2010 Colloids Surface 372 190
Google Scholar
[14] Wang S, Zhao M, Li X, Wei S 2015 J. Appl. Fluid Mech. 8 323
Google Scholar
[15] Wang S W, Li N, Zhao M L, Azese M N 2018 Z. Naturforsch. A 73 825
Google Scholar
[16] Malekanfard A, Ko C H, Li D, Bulloch L, Baldwin A, Wang Y N, Fu L M, Xuan X C 2019 Phys. Fluids 31 022002
Google Scholar
[17] Gul F, Maqbool K, Mann A B 2021 J. Therm. Anal. Calorim. 3 2111
Google Scholar
[18] Mondal P K, Roy M 2021 Electrophoresis 42 2465
Google Scholar
[19] Alfwzan W F, Riaz A, Alammari M, Hejazi H A, EI-Din E T M 2023 Front. Phys. 11 112
Google Scholar
[20] Hoyt J W, Fabula A G 1964 The Effect of Additives on Fluid Friction (US Naval Ordinance Test Station Report
[21] Eringen A C 1966 J. Math. Mech. 16 1
Google Scholar
[22] Papautsky I, Brazzle J, Ameel T, Frazier A B 1999 Sensor. Actuat. A-Phys. 73 101
Google Scholar
[23] Ali N, Hayat T 2008 Comp. Math. Appl. 55 589
Google Scholar
[24] Siddiqui A A, Lakhtakia A 2009 P. Roy. Soc. A-Math. Phy. 465 501
Google Scholar
[25] Wang Y Q, Hayat Tasawar, Oberlack Martin 2011 Appl. Math. Mod. 35 3737
Google Scholar
[26] Misra J C, Chandra S, Shit G C, Kundu P K 2014 Appl. Math. Mech. 35 749
Google Scholar
[27] Ding Z D, Jian Y J, Yang L G 2016 Appl. Math. Mech. 37 769
Google Scholar
[28] Ding Z D, Jian Y J, Wang L, Yang L G 2017 Phys. Fluids 29 082008
Google Scholar
[29] Chaube M K, Yadav A, Tripathi D, Beg O A 2018 Korea-Aust. Rheol. J. 30 89
Google Scholar
[30] Huang H F, Huang K H 2019 Meccanica 54 2151
Google Scholar
[31] Rana S, Nawaz M, Saleem S, Alharbi S O 2020 Phys. Scr. 95 045201
Google Scholar
[32] Zhu W Y 2021 Adv. Geo-Energy. Res. 5 465
Google Scholar
[33] Karampour F, Poshtiri A H, Hadizade A 2022 J. Braz. Soc. Mech. Sci. Eng. 44 198
Google Scholar
[34] Jaiswal S, Yadav P K 2022 Microfluid Nanofluid. 26 100
Google Scholar
[35] Narla V K, Tripathi, Dharmendra, Bhandari D S 2022 Int. J. Ambient. Eng. 43 8193
Google Scholar
[36] Fatunmbi E O, Adeosun A T, Okoya S S 2023 Int. J. Modell. Simul. 43 491
Google Scholar
[37] Rauf A, Sahar N, Siddiq M K, Mustafa F, Mushtaq T, Shehzad S A 2023 Chin. J. Phys. 83 147
Google Scholar
-
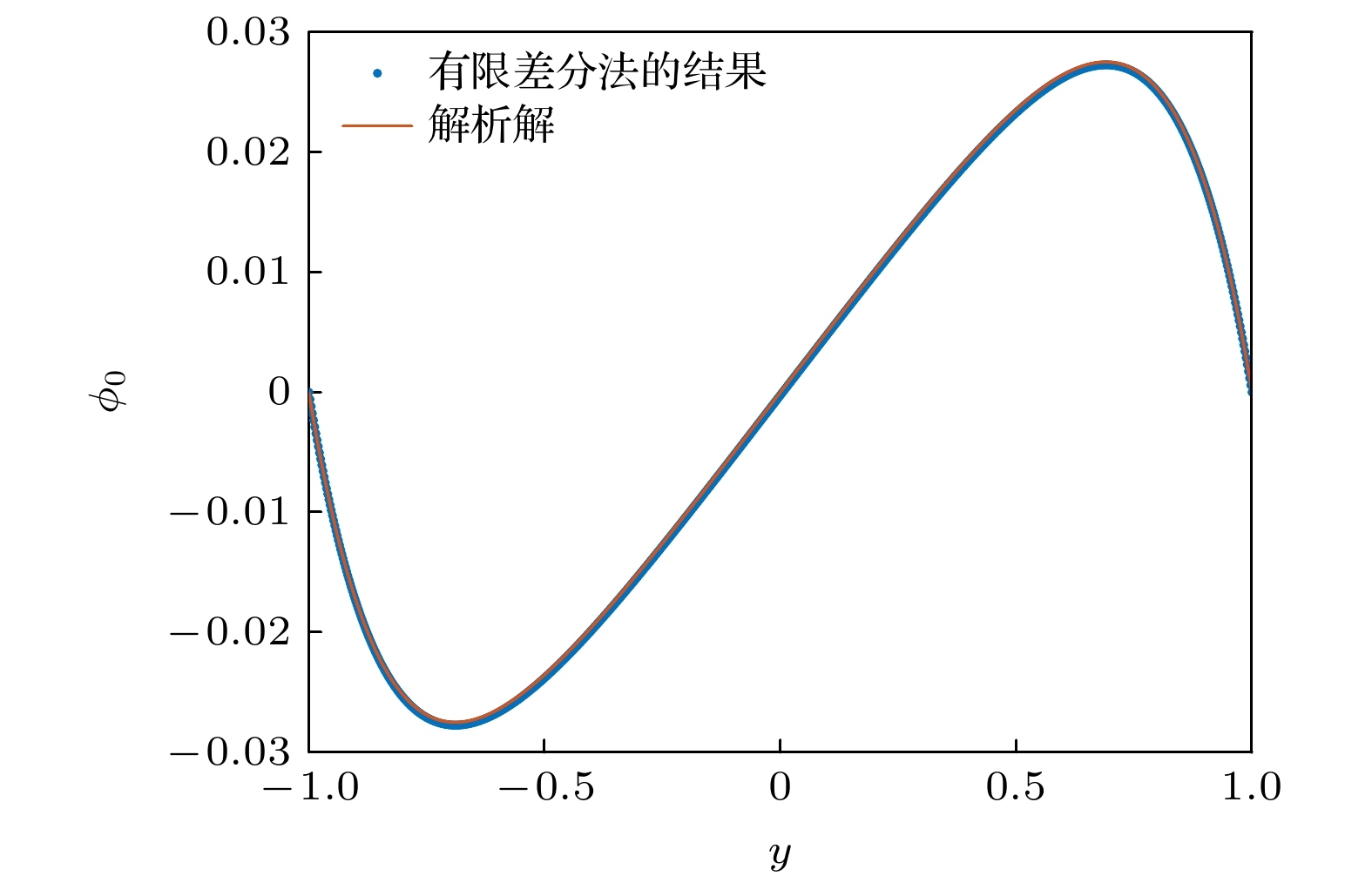
图 2 低Zeta势下电势方程BVP4c所得解、有限差分法的数值解与D-H近似解析解对比图, 其中$ {\psi _0} = 1, \; $$ \beta = 1, m = 5 $
Fig. 2. Comparison of solution of BVP4c, numerical solution of finite difference method and approximate analytical solution of D-H for potential equation at low Zeta potential, where $ {\psi _0} = 1, {\text{ }}\beta = 1, {\text{ }}m = 5 $
图 3 低Zeta势下速度方程有限差分法数值解与D-H近似解析解对比图, 其中$ m = 5, {k_1} = 0.5, \beta = 1, $ $\varOmega = 0.251, $$ {\psi _0} = 1 $
Fig. 3. Comparison of numerical solution of finite difference method and approximate analytical solution of D-H for velocity equation at low Zeta potential, where $ m = 5, $$ {k_1} = 0.5, \beta = 1, \varOmega = 0.251, {\psi _0} = 1 $.
图 4 低Zeta势下微旋转方程有限差分法数值解与D-H近似解析解对比图, 其中$ m = 5,\; {k_1} = 0.5, \;\beta = 1, $$ \varOmega = 0.251, {\psi _0} = 1 $
Fig. 4. Comparison of numerical solution of finite difference method and approximate analytical solution of D-H for microrotation equation at low Zeta potential, where $ m = 5, {k_1} = 0.5, \beta = 1, \varOmega = 0.251, {\psi _0} = 1 $.
图 5 不同Zeta势和$ {k_1} $下无量纲速度分布, 其中$ m = 10, \beta = 1, {\text{ }}\varOmega = 0.251 $ $ ({\text{a}}){\text{ }}{k_1} = 0.5 $; $ ({\text{b}}){\text{ }}{\psi _0} = 2 $
Fig. 5. Dimensionless velocity distribution for different Zeta potentials and $ {k_1} $, where $ m = 10, {\text{ }}\beta = 1, {\text{ }}\varOmega = 0.251 $: $ ({\text{a}}){\text{ }}{k_1} = 0.5 $; $ ({\text{b}}){\text{ }}{\psi _0} = 2 $.
图 6 不同m和$ \varOmega $下无量纲速度分布, 其中$ {\psi _0} = 2, {\text{ }}{k_1} = 0.5, {\text{ }}\beta = 1 $ (a) $ \varOmega $= 0.251; (b) $ \varOmega $= 0.5; (c) $ \varOmega $= 25.1; (d) $ \varOmega $= 251
Fig. 6. Dimensionless velocity distribution for different m and $ \varOmega $, where $ {\psi _0} = 2, {\text{ }}{k_1} = 0.5, {\text{ }}\beta = 1 $: (a) $ \varOmega $=0.251; (b) $ \varOmega $=0.5; (c) $ \varOmega $=25.1; (d) $ \varOmega $=251.
图 7 不同Zeta势和$ {k_1} $下无量纲微旋转分布, 其中$ m = 10, {\text{ }}\beta = 1, {\text{ }}\varOmega = 0.251 $ (a) $ {k_1} = 0.5 $; $ ({\text{b}}){\text{ }}{\psi _0} = 2 $
Fig. 7. Dimensionless micro-rotating profiles distribution for different Zeta potentials and $ {k_1} $, where $ m = 10, {\text{ }}\beta = 1, {\text{ }}\varOmega = 0.251 $: (a) $ {k_1} = 0.5 $; $ ({\text{b}}){\text{ }}{\psi _0} = 2 $.
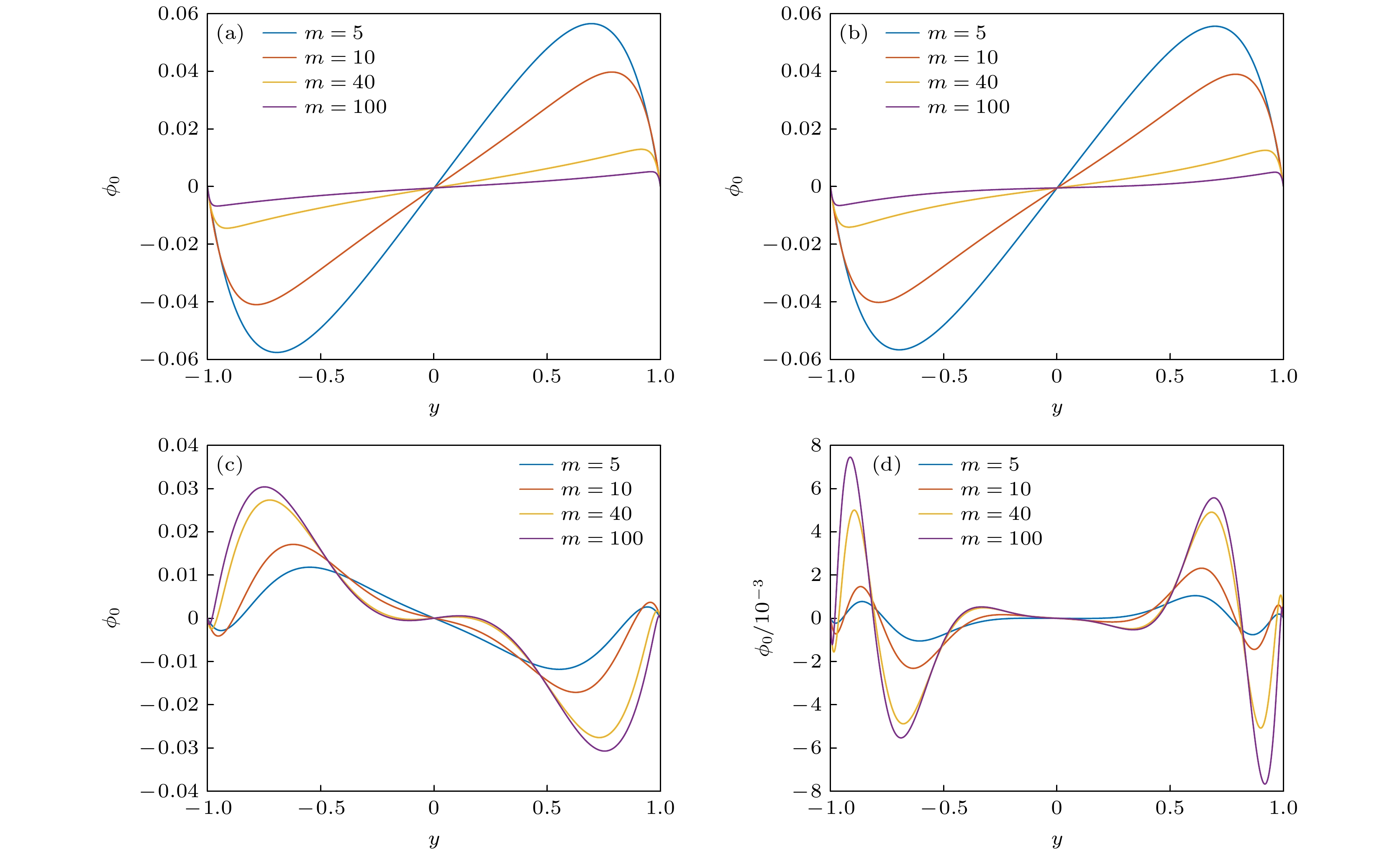
图 8 不同m和$ \varOmega $下无量纲微旋转分布, 其中$ {\psi _0} = 2, {\text{ }}{k_1} = 0.5, {\text{ }}\beta = 1 $ (a) $ \varOmega $=0.251; (b) $ \varOmega $=0.5; (c) $ \varOmega $=25.1; (d) $ \varOmega $=251
Fig. 8. Dimensionless micro-rotation distribution under different m and $ \varOmega $, where $ {\psi _0} = 2, {\text{ }}{k_1} = 0.5, {\text{ }}\beta = 1 $: (a) $ \varOmega $=0.251; (b) $ \varOmega $=0.5; (c) $ \varOmega $=25.1; (d) $ \varOmega $=251.
图 9 不同Zeta势下$ {Q_0} $的变化, 其中$ \varOmega = 0.251, \beta = 1 $ (a) $ {k_1} = 0.5 $; (b) m = 50
Fig. 9. Change of $ {Q_0} $ under different Zeta potentials, where $ \varOmega = 0.251, \beta = 1 $: (a) $ {k_1} = 0.5 $; (b) m = 50.
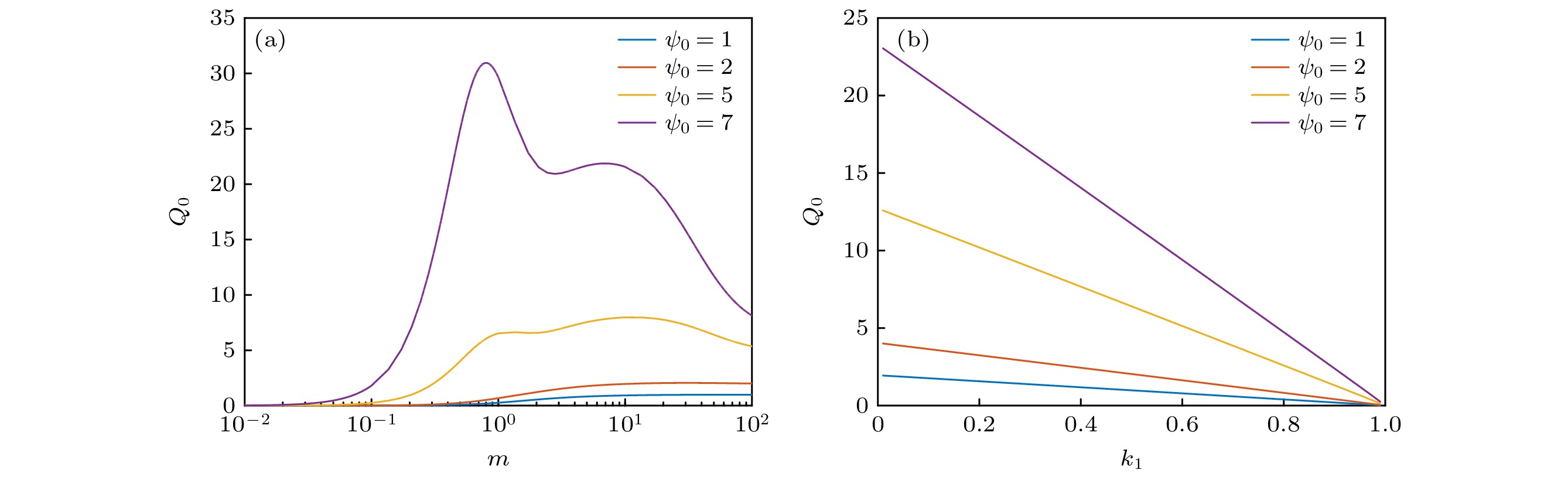
图 10 不同$ {k_1} $和$ \varOmega $下无量纲体积流量振幅与m和$ {k_1} $的关系, 其中$ {\psi _0} = 2, \beta = 1 $ (a) $ \varOmega $=0.251; (b) $ {k_1} $=0.5
Fig. 10. Dependence of amplitude of normalized volume flow rate on m and $ {k_1} $for different $ {k_1} $ and $ \varOmega $, where $ {\psi _0} = 2, \beta = 1 $: (a) $ \varOmega $=0.251; (b) $ {k_1} $=0.5.
图 11 不同Zeta势下$ {W_0} $的变化, 其中$ m = 10, \beta = 1 $ (a) $ \varOmega $=0.251; (b) $ {k_1} $=0.5
Fig. 11. Change of $ {W_0} $ under different Zeta potentials, where $ m = 10, \beta = 1 $: (a) $ \varOmega $=0.251; (b) $ {k_1} $=0.5.
图 12 不同$ m $下无量纲微旋转强度振幅与$ \varOmega $和$ {k_1} $的关系, 其中$ {\psi _0} = 2, \beta = 1 $ (a) $ \varOmega $=0.251; (b) $ {k_1} $=0.5
Fig. 12. Amplitude of dimensionless microrotation strength on $ \varOmega $ and $ {k_1} $ for different $ m $, where $ {\psi _0} = 2, \beta = 1 $: (a) $ \varOmega $=0.251; (b) $ {k_1} $=0.5.
图 13 不同Zeta势下$ {\sigma _{21}} $(a)和$ {\sigma _{12}} $(b)的变化, 其中$ m = 50, \beta = 1, \varOmega = 0.251 $
Fig. 13. Change of $ {\sigma _{21}} $ (a) and $ {\sigma _{12}} $ (b) under different Zeta potentials, where $ m = 50, \beta = 1, \varOmega = 0.251 $.
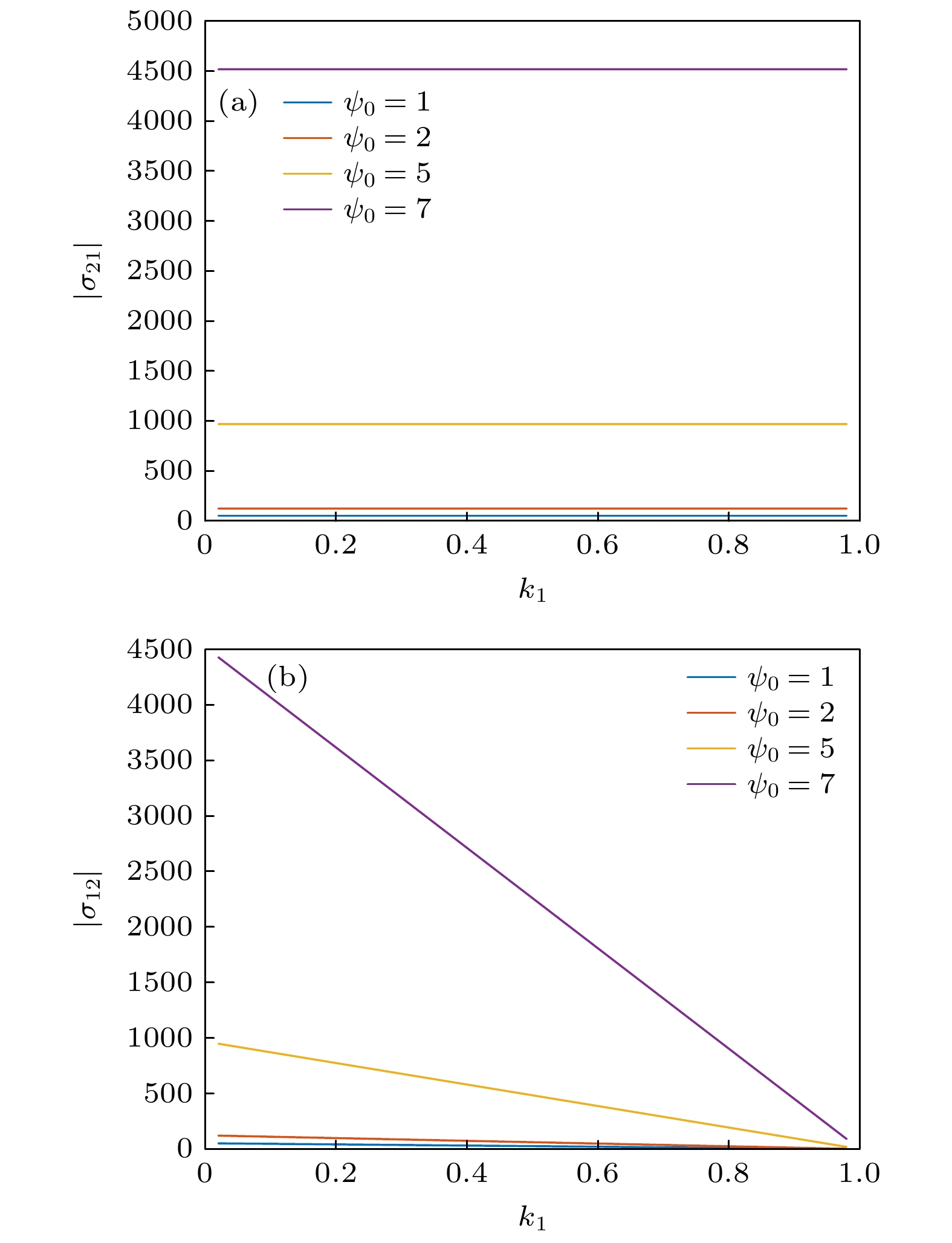
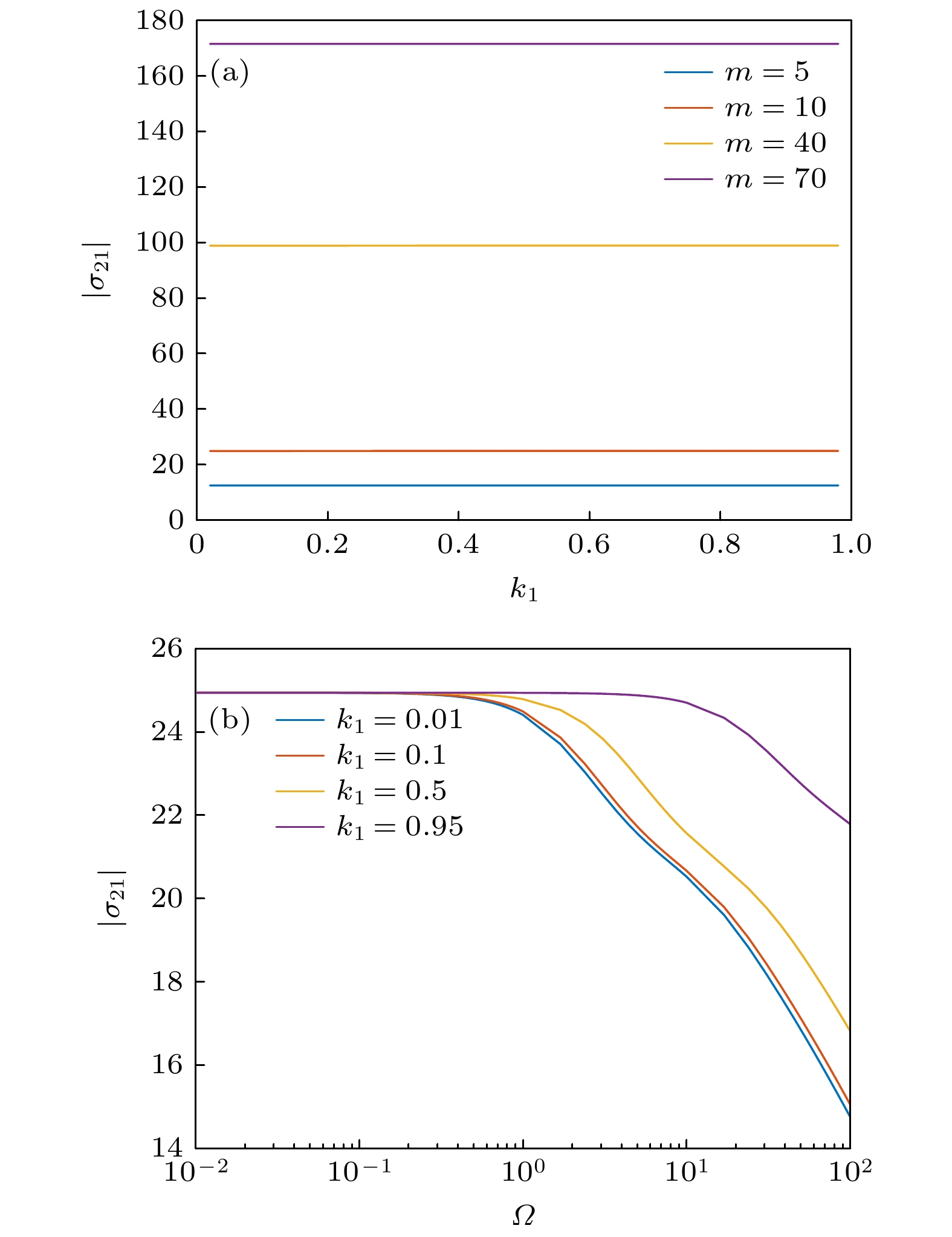
图 14 不同m和$ {k_1} $下壁面剪切应力$ {\sigma _{21}} $与$ {k_1} $和$ \varOmega $的关系, 其中$ {\psi _0} = 2, \beta = 1 $ (a) $ \varOmega $=0.251; (b) m = 10
Fig. 14. Relationship between wall shear stress $ {\sigma _{21}} $and $ {k_1} $ and $ \varOmega $ under different m and $ {k_1} $, where $ {\psi _0} = 2, \beta = 1 $: (a) $ \varOmega $= 0.251; (b) m = 10.
图 15 不同m和$ {k_1} $下壁面剪切应力$ {\sigma _{12}} $与$ {k_1} $和$ \varOmega $的关系, 其中$ {\psi _0} = 2, \beta = 1 $ (a) $ \varOmega $=0.251; (b) m = 10
Fig. 15. Relationship between wall shear stress $ {\sigma _{12}} $and $ {k_1} $ and $ \varOmega $ under different m and $ {k_1} $, where $ {\psi _0} = 2, \beta = 1 $: (a) $ \varOmega $=0.251; (b) m = 10.
-
[1] Osuga T, Sakamoto H, Takagi T 1996 J. Phys. Soc. Jpn. 65 1854
Google Scholar
[2] Polevoi V V, Bilova T E, Shevtsov Y I 2003 Biol. Bull 30 133
Google Scholar
[3] Dem'yanov A Y, Dinariev O Y, Sharaborin E L 2020 Russ. Phys. J. 63 113
Google Scholar
[4] Masuduzzaman M, Kim B H 2022 Langmuir 38 7244
Google Scholar
[5] Reuss F F 1809 Proc. Imp. Soc. Nat. Mos. 3 327
[6] Patankar N A, Hu H H 1998 Anal. Chem. 70 1870
Google Scholar
[7] Gleeson J P 2002 J. Colloid Interface Sci. 249 217
Google Scholar
[8] Fu L M, Lin J Y, Yang R J 2003 J. Colloid Interface Sci. 258 266
Google Scholar
[9] Stone H A, Stroock A D, Ajdari A 2004 Annu. Rev. Fluid Mech. 36 381
Google Scholar
[10] Park H M, Lee J S, Kim T W 2007 J. Colloid Interface Sci. 315 731
Google Scholar
[11] Jian Y J, Yang L G, Liu Q S 2010 Phys. Fluids 22 042001
Google Scholar
[12] Yoshida H 2016 Comput. Fluids 124 237
Google Scholar
[13] Nosrati R, Hadigol M, Raisee M 2010 Colloids Surface 372 190
Google Scholar
[14] Wang S, Zhao M, Li X, Wei S 2015 J. Appl. Fluid Mech. 8 323
Google Scholar
[15] Wang S W, Li N, Zhao M L, Azese M N 2018 Z. Naturforsch. A 73 825
Google Scholar
[16] Malekanfard A, Ko C H, Li D, Bulloch L, Baldwin A, Wang Y N, Fu L M, Xuan X C 2019 Phys. Fluids 31 022002
Google Scholar
[17] Gul F, Maqbool K, Mann A B 2021 J. Therm. Anal. Calorim. 3 2111
Google Scholar
[18] Mondal P K, Roy M 2021 Electrophoresis 42 2465
Google Scholar
[19] Alfwzan W F, Riaz A, Alammari M, Hejazi H A, EI-Din E T M 2023 Front. Phys. 11 112
Google Scholar
[20] Hoyt J W, Fabula A G 1964 The Effect of Additives on Fluid Friction (US Naval Ordinance Test Station Report
[21] Eringen A C 1966 J. Math. Mech. 16 1
Google Scholar
[22] Papautsky I, Brazzle J, Ameel T, Frazier A B 1999 Sensor. Actuat. A-Phys. 73 101
Google Scholar
[23] Ali N, Hayat T 2008 Comp. Math. Appl. 55 589
Google Scholar
[24] Siddiqui A A, Lakhtakia A 2009 P. Roy. Soc. A-Math. Phy. 465 501
Google Scholar
[25] Wang Y Q, Hayat Tasawar, Oberlack Martin 2011 Appl. Math. Mod. 35 3737
Google Scholar
[26] Misra J C, Chandra S, Shit G C, Kundu P K 2014 Appl. Math. Mech. 35 749
Google Scholar
[27] Ding Z D, Jian Y J, Yang L G 2016 Appl. Math. Mech. 37 769
Google Scholar
[28] Ding Z D, Jian Y J, Wang L, Yang L G 2017 Phys. Fluids 29 082008
Google Scholar
[29] Chaube M K, Yadav A, Tripathi D, Beg O A 2018 Korea-Aust. Rheol. J. 30 89
Google Scholar
[30] Huang H F, Huang K H 2019 Meccanica 54 2151
Google Scholar
[31] Rana S, Nawaz M, Saleem S, Alharbi S O 2020 Phys. Scr. 95 045201
Google Scholar
[32] Zhu W Y 2021 Adv. Geo-Energy. Res. 5 465
Google Scholar
[33] Karampour F, Poshtiri A H, Hadizade A 2022 J. Braz. Soc. Mech. Sci. Eng. 44 198
Google Scholar
[34] Jaiswal S, Yadav P K 2022 Microfluid Nanofluid. 26 100
Google Scholar
[35] Narla V K, Tripathi, Dharmendra, Bhandari D S 2022 Int. J. Ambient. Eng. 43 8193
Google Scholar
[36] Fatunmbi E O, Adeosun A T, Okoya S S 2023 Int. J. Modell. Simul. 43 491
Google Scholar
[37] Rauf A, Sahar N, Siddiq M K, Mustafa F, Mushtaq T, Shehzad S A 2023 Chin. J. Phys. 83 147
Google Scholar
下载:
计量
- 文章访问数: 723
- PDF下载量: 22
- 被引次数: 0
