一维非厄米十字晶格中的退局域-局域转变

刘辉; 陆展鹏; 徐志浩

doi:10.7498/aps.73.20240510

摘要

本文研究了在具有平带的一维非厄米十字晶格中引入准周期调制所诱导的退局域-局域的转变. 通过解析推导和数值分析分形维度和能谱的实复转变, 发现在非厄米单平带十字晶格中引入对称的准周期调制会引起扩展相到局域相的转变, 而反对称准周期调制能够诱导出精确的迁移率边. 在非厄米全平带十字晶格中, 对称的准周期调制情况下, 系统一直处于局域相, 当引入反对称的准周期调制时, 系统具有从多重分形相到局域相的转变. 该研究结果为非厄米平带的局域化性质研究提供了参考.

关键词:

Abstract

In this work, we investigate the influence of quasi-periodic modulation on the localization properties of one-dimensional non-Hermitian cross-stitch lattices with flat bands. The crystalline Hamiltonian for this non-Hermitian cross-stitch lattice is given by: $\hat{H}=\displaystyle\sum\limits_{n}\left[t(a_n^{\dagger} b_n + b_n^{\dagger}a_n ) + J{\mathrm{e}}^{h}\left(a_n^{\dagger}b_{n + 1} + a_n^{\dagger} a_{n + 1} + Ab_n^{\dagger}a_{n + 1} + Ab_n^{\dagger}b_{n + 1}\right) + J{\mathrm{e}}^{ - h} \left(Aa_{n + 1}^{\dagger}b_n + a_{n + 1}^{\dagger}a_n + b_{n + 1}^{\dagger}a_n + Ab_{n + 1}^{\dagger}b_n\right)\right] $with $A =\pm 1$. When A = 1, the clean lattice supports two bands with dispersion relations $E_0=- t, $$ E_1=4\cos (k - {\mathrm{i}}h) + t$. The compact localized states (CLSs) within the flat band E₀ are localized in one unit cell, indicating that the system is characterized by the U = 1 class. Conversely, for A = –1, there are two flat bands in the system: $E_{\pm}=\pm\sqrt{t^2 + 4}$. The CLSs within the flat bands are localized in two unit cells, indicating that the system is marked by the U = 2 class. After introducing quasi-periodic modulations $\varepsilon_n^{\beta}=\lambda_{\beta}\cos(2\pi\alpha n + \phi_{\beta})$ ($\beta=\{a,b\}$), delocalization-localization transitions can be observed by numerically calculating the fractal dimension D₂ and imaginary part of the energy spectrum $\ln{|{\rm{Im}}(E)|}$. Our findings indicate that the symmetry of quasi-periodic modulations plays an important role in determining the localization properties of the system. For the case of $U=1$, the symmetric quasi-periodic modulation leads to two independent spectra $\sigma_f$ and $\sigma_p$. The $\sigma_f$ retains its compact properties, while the $\sigma_p$ owns an extended-localized transition at $\lambda_{{\mathrm{c}}1}=4M$ with $M=\max\{{\mathrm{e}}^{h},\;{\mathrm{e}}^{ - h}\}$. However, in the case of antisymmetric modulation, the system exhibits an exact mobility edge $\lambda_{{\mathrm{c}}2}=2\sqrt{2|E - t|M}$. For the U = 2 class, all the eigenstates remain localized under any symmetric quasi-periodic modulation. In the case of antisymmetric modulation, all states transition from multifractal to localized states as the modulation strength increases, with a critical point at $\lambda_{{\mathrm{c}}3}=4M$. This work expands the understanding of localization properties in non-Hermitian flat-band systems and provides a new perspective on delocalization-localization transitions.

Keywords:

作者及机构信息

1.
山西大学理论物理研究所, 量子光学与光量子器件国家重点实验室, 太原　030006

2.
山西大学, 极端光学协同创新中心, 太原　030006

通信作者: 徐志浩, xuzhihao@sxu.edu.cn

基金项目: 国家自然科学基金(批准号: 12375016)、山西省基础研究计划(批准号: 20210302123442)、北京凝聚态物理国家实验室(批准号: 2023BNLCMPKF001)和山西省“1331工程”重点学科建设计划资助的课题.

Authors and contacts

1.
State Key Laboratory of Quantum Optics and Quantum Optics Devices, Institute of Theoretical Physics, Shanxi University, Taiyuan 030006, China

2.
Collaborative Innovation Center of Extreme Optics, Shanxi University, Taiyuan 030006, China

Corresponding author: Xu Zhi-Hao, xuzhihao@sxu.edu.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant No. 12375016), the Fundamental Research Program of Shanxi Province, China (Grant No. 20210302123442), the Beijing National Laboratory for Condensed Matter Physics (Grant No. 2023BNLCMPKF001), and the Fund for Shanxi “1331 Project” Key Subjects, China.

文章全文

参考文献

[1]	Anderson P W 1958 Phys. Rev. 109 1492 Google Scholar
[2]	Billy J, Josse V, Zuo Z, Bernard A, Hambrecht B, Lugan P, Clément D, Sanchez-Palencia L, Bouyer P, Aspect A 2008 Nature 453 891 Google Scholar
[3]	Hu H, Strybulevych A, Page J H, Skipetrov S E, van Tiggelen B A 2008 Nat. Phys. 4 945 Google Scholar
[4]	Pradhan P, Sridhar S 2000 Phys. Rev. Lett. 85 2360 Google Scholar
[5]	Mott N 1987 J. Phys. C 20 3075 Google Scholar
[6]	Wang Y, Zhang L, Sun W, Poon T F J, Liu X J 2022 Phys. Rev. B 106 L140203 Google Scholar
[7]	Yamamoto K, Aharony A, Entin-Wohlman O, Hatano N 2017 Phys. Rev. B 96 155201 Google Scholar
[8]	Aubry S, André G 1980 Ann. Isr. Phys. Soc. 3 133
[9]	Longhi S 2019 Phys. Rev. Lett. 122 237601 Google Scholar
[10]	Xu Z, Xia X, Chen S 2022 Sci. China: Phys. Mech. Astron. 65 227211 Google Scholar
[11]	Biddle J, Das Sarma S 2010 Phys. Rev. Lett. 104 070601 Google Scholar
[12]	Ganeshan S, Pixley J H, Sarma S D 2015 Phys. Rev. Lett. 114 146601 Google Scholar
[13]	Leykam D, Flach S, Bahat-Treidel O, Desyatnikov A S 2013 Phys. Rev. B 88 224203 Google Scholar
[14]	Zhang W, Addison Z, Trivedi N 2021 Phys. Rev. B 104 235202 Google Scholar
[15]	Leykam D, Bodyfelt J D, Desyatnikov A S, Flach S 2017 Eur. Phy. J. B 90 1 Google Scholar
[16]	Maimaiti W, Andreanov A 2021 Phys. Rev. B 104 035115 Google Scholar
[17]	Bodyfelt D, Leykam D, Danieli C, Yu X, Flach S 2014 Phys. Rev. Lett. 113 236403 Google Scholar
[18]	Danieli C, Bodyfelt J D, Flach S 2015 Phys. Rev. B 91 235134 Google Scholar
[19]	Lee S, Andreanov A, Flach S 2023 Phys. Rev. B 107 014204 Google Scholar
[20]	Lee S, Flach S, Andreanov A 2023 Chaos 33 073125 Google Scholar
[21]	Ahmed A, Ramachandran A, Khaymovich I M, Sharma A 2022 Phys. Rev. B 106 205119 Google Scholar
[22]	Liu C, Jiang H, Chen S 2019 Phys. Rev. B 99 125103 Google Scholar
[23]	Liu C, Chen S 2019 Phys. Rev. B 100 144106 Google Scholar
[24]	Bender C M, Boettcher S 1998 Phys. Rev. Lett. 80 5243 Google Scholar
[25]	Zhao H, Miao P, Teimourpour M H, Malzard S, ElGanainy R, Schomerus H, Feng L 2018 Nat. Commun. 9 981 Google Scholar
[26]	Jiang H, Lang L J, Yang C, Zhu S L, Chen S 2019 Phys. Rev. B 100 054301 Google Scholar
[27]	Yao S, Song F, Wang Z 2018 Phys. Rev. Lett. 121 136802 Google Scholar
[28]	Yao S, Wang Z 2018 Phys. Rev. Lett. 121 086803 Google Scholar
[29]	Hatano N, Nelson D R 1996 Phys. Rev. Lett. 77 570 Google Scholar
[30]	Hatano N, Nelson D R 1997 Phys. Rev. B 56 8651 Google Scholar
[31]	Hatano N, Nelson D R 1998 Phys. Rev. B 58 8384 Google Scholar
[32]	Flach S, Leykam D, Bodyfelt J D, Matthies P, Desyatnikov A S 2014 Europhys. Lett. 105 30001 Google Scholar
[33]	Miroshnichenko A E, Flach S, Kivshar Y S 2010 Rev. Mod. Phys. 82 2257 Google Scholar
[34]	Evers F, Mirlin A D 2008 Rev. Mod. Phys. 80 1355 Google Scholar
[35]	Macé N, Alet F, Laflorencie N 2019 Phys. Rev. Lett. 123 180601 Google Scholar
[36]	Liu H, Lu Z, Xia X, Xu Z 2024 arXiv: 2311.03166 [cond-mat.dis-nn]
[37]	Zeng Q B, Chen S, Lü R 2017 Phys. Rev. A 95 062118 Google Scholar
[38]	Tang L Z, Zhang G Q, Zhang L F, Zhang D W 2021 Phys. Rev. A 103 033325 Google Scholar
[39]	Kawabata K, Shiozaki K, Ueda M, Sato M 2019 Phys. Rev. X 9 041015 Google Scholar

施引文献

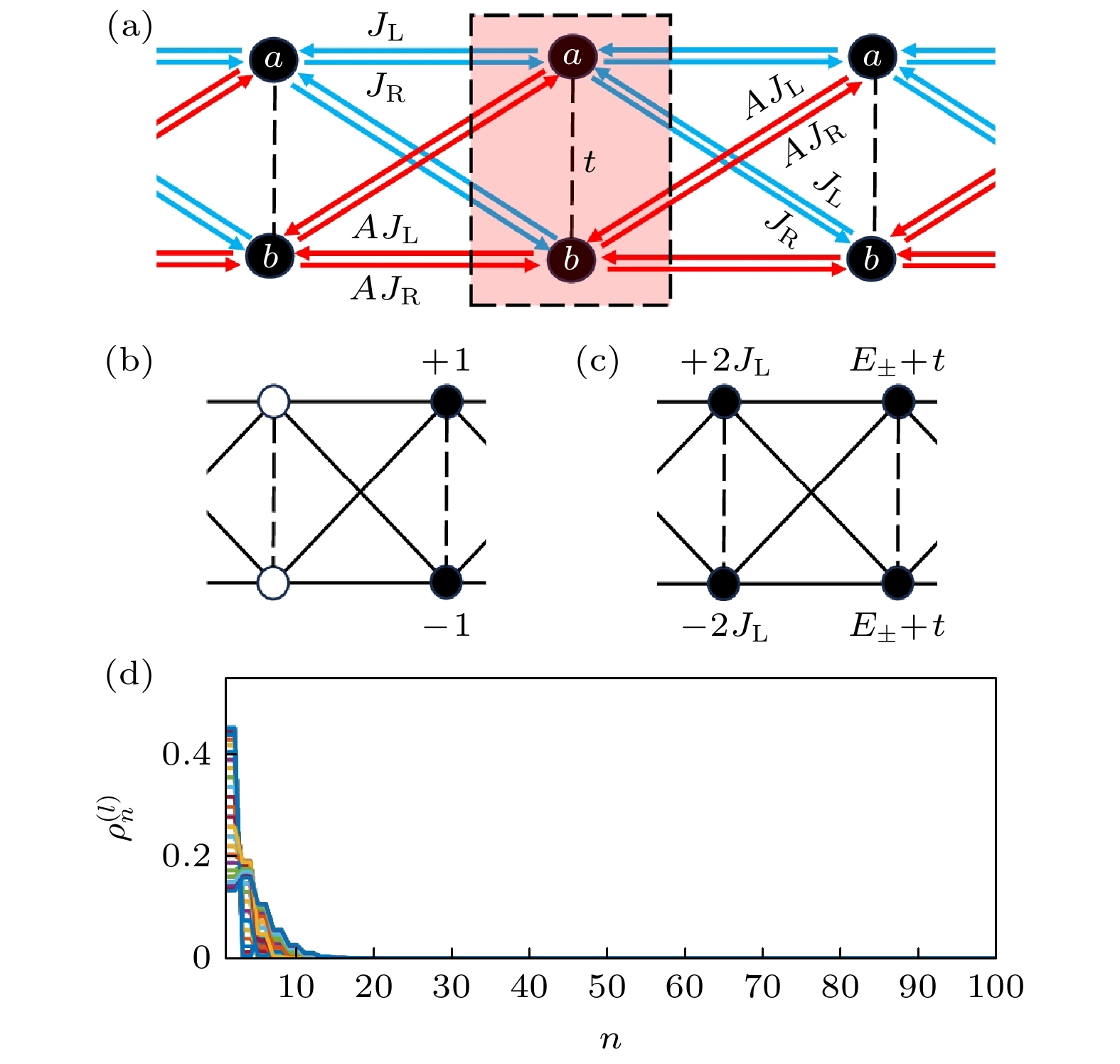
图 1 干净晶格情况　(a) 一维非厄米十字晶格示意图; (b) $ U=1 $类非厄米十字晶格的CLS占据; (c) $ U=2 $类非厄米十字晶格的CLS占据; (d)开边界条件下, $ U=1 $类十字晶格色散带中所有本征态的密度分布$ \rho_n^{(l)} $. 这里的参数选取$ h=0.6 $, $ t=2 $, $ L=100 $

Fig. 1. Crystalline case: (a) Schematic diagram of the one-dimensional non-Hermitian cross-stitch lattice; (b) CLS occupations of the $ U=1 $ class non-Hermitian cross-stitch lattice with $ A=1 $; (c) CLS occupations of the $ U=2 $ class non-Hermitian cross-stitch lattice with $ A=-1 $; (d) density distributions $ \rho_n^{(l)} $ for all the eigenstates in dispersive bands of the cross-stitch lattice under open bonudary conditions. Here, $ h=0.6 $, $ t=2 $, $ L=100 $

下载: 全尺寸图片幻灯片

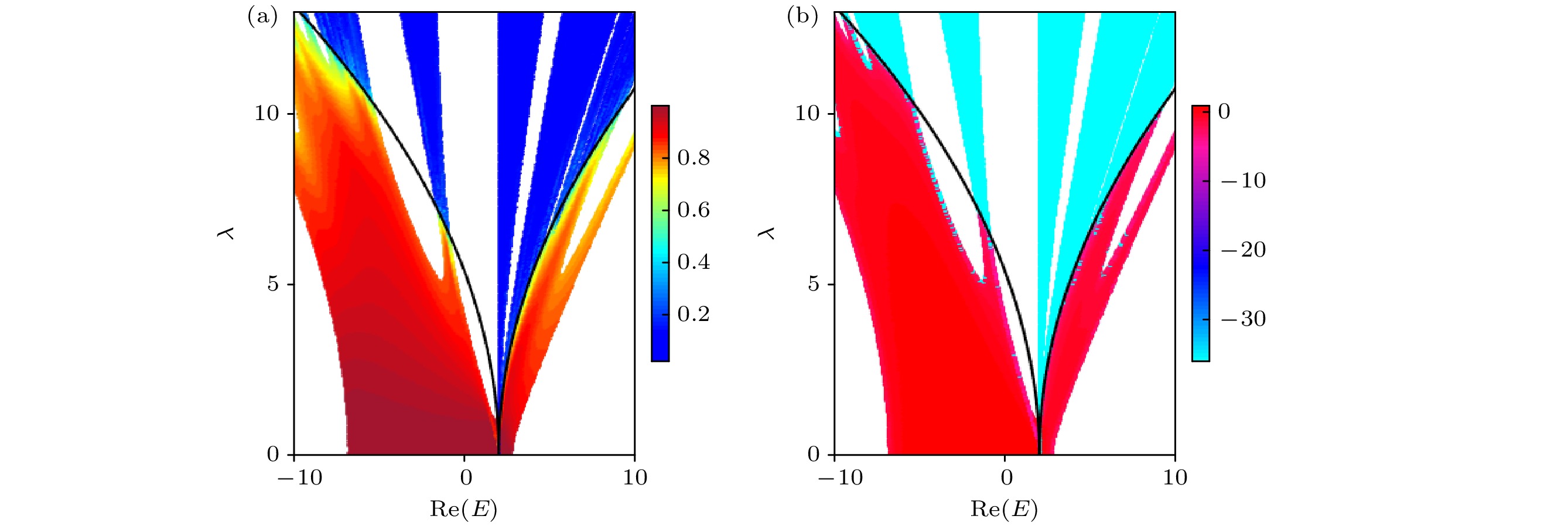
图 2 对称情况时, $ U=1 $ 类非厄米十字晶格的局域化性质　(a) $ \sigma_p $谱的分型维度$ D_2^{(l)} $随着能量实部$ {\rm{Re}}(E) $和无序强度$ \lambda $的变化, 颜色表示分形维度$ D_2^{(l)} $的大小. (b) $ \sigma_p $谱的能量虚部$ \ln{|{\rm{Im}}(E)|} $随着能量实部$ {\rm{Re}}(E) $和无序强度$ \lambda $的变化, 颜色表示$ \ln{|{\rm{Im}}(E)|} $的大小, 实线表示扩展-局域转变, $ \sigma_f $被省略, 边界用虚线表示. (c)$ \lambda=5 $时, $ \sigma_p $所对应的能谱. (d)$ \lambda=10 $时, $ \sigma_p $所对应的能谱. 这里$ L=1000 $

Fig. 2. Symmetric case of the $ U=1 $ class non-Hermitian cross-stitch lattice: (a) Real part of the spectrum $ \sigma_p $ as a function of $ \lambda $, where the color denotes the value of the fractal dimension $ D_2^{(l)} $. (b) $ \ln{|{\rm{Im}}(E)|} $ of $ \sigma_p $ as a function of $ \lambda $ and $ {\rm{Re}}(E) $, where the color denotes the value of $ \ln{|{\rm{Im}}(E)|} $. Black solid lines represent the delocalization-localization transition. The spectrum $ \sigma_{f} $ is omitted, but its boundaries are indicated by black dashed lines. (c) Energy spectrum of $ \sigma_p $ with $ \lambda=5 $. (d) Energy spectrum of $ \sigma_p $ with $ \lambda=10 $. Here, $ L=1000 $.

下载: 全尺寸图片幻灯片

图 3 反对称情况时, $ U=1 $ 类非厄米十字型晶格的局域化　(a)分型维度$ D_2^{(l)} $随着能量实部$ {\rm{Re}}(E) $和无序强度$ \lambda $的变化; (b)能量虚部$ \ln{|{\rm{Im}}(E)|} $随着能量实部$ {\rm{Re}}(E) $和无序强度$ \lambda $的变化. 实线表示迁移率边. 这里$ L=1000 $

Fig. 3. Antisymmetric case of the $ U=1 $ class non-Hermitian cross-stitch lattice: (a) $D_2^{(l)} $ of the spectrum as a function of $ \lambda $, where the color denotes the value of the fractal dimension $ D_2^{(l)} $; (b) $ \ln{|{\rm{Im}}(E)|} $ of the spectrum as a function of $ \lambda $ and $ {\rm{Re}}(E) $, where the color denotes the value of $ \ln{|{\rm{Im}}(E)|} $. The black solid lines represent the mobility edges. Here, $ L=1000 $.

下载: 全尺寸图片幻灯片

图 4 反对称情况时, $ U=2 $类非厄米十字晶格的局域化　(a)分型维度$ D_2^{(l)} $随着能量实部$ {\rm{Re}}(E) $和无序强度$ \lambda $的变化, 颜色表示分形维度$ D_2^{(l)} $的大小. (b)能量虚部$ \ln{|{\rm{Im}}(E)|} $随着能量实部$ {\rm{Re}}(E) $和无序强度$ \lambda $的变化, 颜色表示$ \ln{|{\rm{Im}}(E)|} $的大小, 实线表示多重分形-局域的转变, 这里$ L=1000 $. (c)多重分形区域的MIPR标度分析, 插图为局域区域的MIPR标度分析

Fig. 4. Antisymmetric case of $ U=2 $ non-Hermitian cross-stitch lattice: (a) $D_2^{(l)} $ of the spectrum as a function of $ \lambda $ and Re(E), where the color denotes the value of the fractal dimension $ D_2^{(l)} $. (b) $ \ln{|{\rm{Im}}(E)|} $ of the spectrum as a function of $ \lambda $ and $ {\rm{Re}}(E) $, where the color denotes the value of $ \ln{|{\rm{Im}}(E)|} $. The black solid lines represent the multifractal-to-localized transition. Here, $ L=1000 $. (c) The MIPR scaling of multifractal regions for different $ \lambda $. The inset shows the MIPR scaling of localized regions for $ \lambda=10 $.

下载: 全尺寸图片幻灯片

map

[1]	Anderson P W 1958 Phys. Rev. 109 1492 Google Scholar
[2]	Billy J, Josse V, Zuo Z, Bernard A, Hambrecht B, Lugan P, Clément D, Sanchez-Palencia L, Bouyer P, Aspect A 2008 Nature 453 891 Google Scholar
[3]	Hu H, Strybulevych A, Page J H, Skipetrov S E, van Tiggelen B A 2008 Nat. Phys. 4 945 Google Scholar
[4]	Pradhan P, Sridhar S 2000 Phys. Rev. Lett. 85 2360 Google Scholar
[5]	Mott N 1987 J. Phys. C 20 3075 Google Scholar
[6]	Wang Y, Zhang L, Sun W, Poon T F J, Liu X J 2022 Phys. Rev. B 106 L140203 Google Scholar
[7]	Yamamoto K, Aharony A, Entin-Wohlman O, Hatano N 2017 Phys. Rev. B 96 155201 Google Scholar
[8]	Aubry S, André G 1980 Ann. Isr. Phys. Soc. 3 133
[9]	Longhi S 2019 Phys. Rev. Lett. 122 237601 Google Scholar
[10]	Xu Z, Xia X, Chen S 2022 Sci. China: Phys. Mech. Astron. 65 227211 Google Scholar
[11]	Biddle J, Das Sarma S 2010 Phys. Rev. Lett. 104 070601 Google Scholar
[12]	Ganeshan S, Pixley J H, Sarma S D 2015 Phys. Rev. Lett. 114 146601 Google Scholar
[13]	Leykam D, Flach S, Bahat-Treidel O, Desyatnikov A S 2013 Phys. Rev. B 88 224203 Google Scholar
[14]	Zhang W, Addison Z, Trivedi N 2021 Phys. Rev. B 104 235202 Google Scholar
[15]	Leykam D, Bodyfelt J D, Desyatnikov A S, Flach S 2017 Eur. Phy. J. B 90 1 Google Scholar
[16]	Maimaiti W, Andreanov A 2021 Phys. Rev. B 104 035115 Google Scholar
[17]	Bodyfelt D, Leykam D, Danieli C, Yu X, Flach S 2014 Phys. Rev. Lett. 113 236403 Google Scholar
[18]	Danieli C, Bodyfelt J D, Flach S 2015 Phys. Rev. B 91 235134 Google Scholar
[19]	Lee S, Andreanov A, Flach S 2023 Phys. Rev. B 107 014204 Google Scholar
[20]	Lee S, Flach S, Andreanov A 2023 Chaos 33 073125 Google Scholar
[21]	Ahmed A, Ramachandran A, Khaymovich I M, Sharma A 2022 Phys. Rev. B 106 205119 Google Scholar
[22]	Liu C, Jiang H, Chen S 2019 Phys. Rev. B 99 125103 Google Scholar
[23]	Liu C, Chen S 2019 Phys. Rev. B 100 144106 Google Scholar
[24]	Bender C M, Boettcher S 1998 Phys. Rev. Lett. 80 5243 Google Scholar
[25]	Zhao H, Miao P, Teimourpour M H, Malzard S, ElGanainy R, Schomerus H, Feng L 2018 Nat. Commun. 9 981 Google Scholar
[26]	Jiang H, Lang L J, Yang C, Zhu S L, Chen S 2019 Phys. Rev. B 100 054301 Google Scholar
[27]	Yao S, Song F, Wang Z 2018 Phys. Rev. Lett. 121 136802 Google Scholar
[28]	Yao S, Wang Z 2018 Phys. Rev. Lett. 121 086803 Google Scholar
[29]	Hatano N, Nelson D R 1996 Phys. Rev. Lett. 77 570 Google Scholar
[30]	Hatano N, Nelson D R 1997 Phys. Rev. B 56 8651 Google Scholar
[31]	Hatano N, Nelson D R 1998 Phys. Rev. B 58 8384 Google Scholar
[32]	Flach S, Leykam D, Bodyfelt J D, Matthies P, Desyatnikov A S 2014 Europhys. Lett. 105 30001 Google Scholar
[33]	Miroshnichenko A E, Flach S, Kivshar Y S 2010 Rev. Mod. Phys. 82 2257 Google Scholar
[34]	Evers F, Mirlin A D 2008 Rev. Mod. Phys. 80 1355 Google Scholar
[35]	Macé N, Alet F, Laflorencie N 2019 Phys. Rev. Lett. 123 180601 Google Scholar
[36]	Liu H, Lu Z, Xia X, Xu Z 2024 arXiv: 2311.03166 [cond-mat.dis-nn]
[37]	Zeng Q B, Chen S, Lü R 2017 Phys. Rev. A 95 062118 Google Scholar
[38]	Tang L Z, Zhang G Q, Zhang L F, Zhang D W 2021 Phys. Rev. A 103 033325 Google Scholar
[39]	Kawabata K, Shiozaki K, Ueda M, Sato M 2019 Phys. Rev. X 9 041015 Google Scholar

[1]	王宇佳, 徐志浩. 周期驱动非互易Aubry-André模型中的多重分形态和迁移率边. , 2025, 74(9): 097201. doi: 10.7498/aps.74.20241633
[2]	郝佳鑫, 徐志浩. 复相互作用调制的两粒子系统中的局域化转变. , 2025, 74(6): 067201. doi: 10.7498/aps.74.20241691
[3]	冯曦曦, 陈文, 高先龙. 量子信息中的度量空间方法在准周期系统中的应用. , 2024, 73(4): 040501. doi: 10.7498/aps.73.20231605
[4]	古燕, 陆展鹏. 非厄米耦合链中的局域化转变. , 2024, 73(19): 197101. doi: 10.7498/aps.73.20240976
[5]	刘敬鹄, 徐志浩. 随机两体耗散诱导的非厄米多体局域化. , 2024, 73(7): 077202. doi: 10.7498/aps.73.20231987
[6]	陆展鹏, 徐志浩. 具有平带的一维十字型晶格中重返局域化现象. , 2024, 73(3): 037202. doi: 10.7498/aps.73.20231393
[7]	李竞, 丁海涛, 张丹伟. 非厄米哈密顿量中的量子Fisher信息与参数估计. , 2023, 72(20): 200601. doi: 10.7498/aps.72.20230862
[8]	刘佳琳, 庞婷方, 杨孝森, 王正岭. 无序非厄米Su-Schrieffer-Heeger中的趋肤效应. , 2022, 71(22): 227402. doi: 10.7498/aps.71.20221151
[9]	张禧征, 王鹏, 张坤亮, 杨学敏, 宋智. 非厄米临界动力学及其在量子多体系统中的应用. , 2022, 71(17): 174501. doi: 10.7498/aps.71.20220914
[10]	侯博, 曾琦波. 非厄米镶嵌型二聚化晶格. , 2022, 71(13): 130302. doi: 10.7498/aps.71.20220890
[11]	高雪儿, 李代莉, 刘志航, 郑超. 非厄米系统的量子模拟新进展. , 2022, 71(24): 240303. doi: 10.7498/aps.71.20221825
[12]	祝可嘉, 郭志伟, 陈鸿. 实验观测非厄米系统奇异点的手性翻转现象. , 2022, 71(13): 131101. doi: 10.7498/aps.71.20220842
[13]	吴瑾, 陆展鹏, 徐志浩, 郭利平. 由超辐射引起的迁移率边和重返局域化. , 2022, 71(11): 113702. doi: 10.7498/aps.71.20212246
[14]	傅聪, 叶梦浩, 赵晖, 陈宇光, 鄢永红. 共轭聚合物链中光激发过程的无序效应. , 2021, 70(11): 117201. doi: 10.7498/aps.70.20201801
[15]	侯碧辉, 刘凤艳, 岳明, 王克军. 纳米金属镝的传导电子定域化. , 2011, 60(1): 017201. doi: 10.7498/aps.60.017201
[16]	丁锐, 金亚秋, 小仓久直. 二维随机介质中柱面波传播及其局域性的随机泛函分析. , 2010, 59(6): 3674-3685. doi: 10.7498/aps.59.3674
[17]	李晓春, 高俊丽, 刘绍娥, 周科朝, 黄伯云. 无序对二维声子晶体平板负折射成像的影响. , 2010, 59(1): 376-380. doi: 10.7498/aps.59.376
[18]	曹永军, 杨旭, 姜自磊. 弹性波通过一维复合材料系统的透射性质. , 2009, 58(11): 7735-7740. doi: 10.7498/aps.58.7735
[19]	许兴胜, 陈弘达, 张道中. 非晶光子晶体中的光子局域化. , 2006, 55(12): 6430-6434. doi: 10.7498/aps.55.6430
[20]	刘小良, 徐慧, 马松山, 宋招权. 一维无序二元固体中电子局域性质的研究. , 2006, 55(6): 2949-2954. doi: 10.7498/aps.55.2949

计量

文章访问数: 2839
PDF下载量: 69
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

一维非厄米十字晶格中的退局域-局域转变