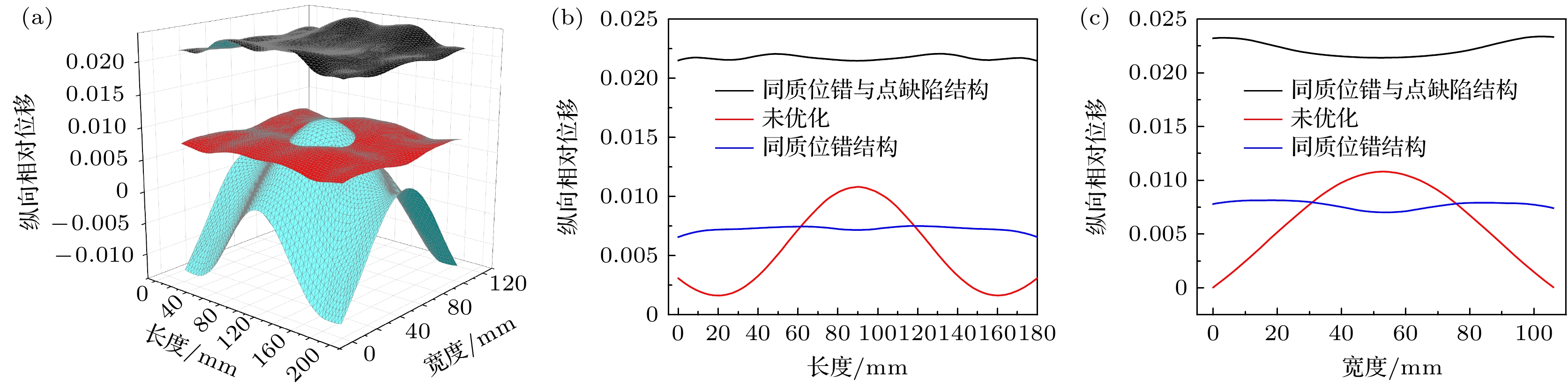
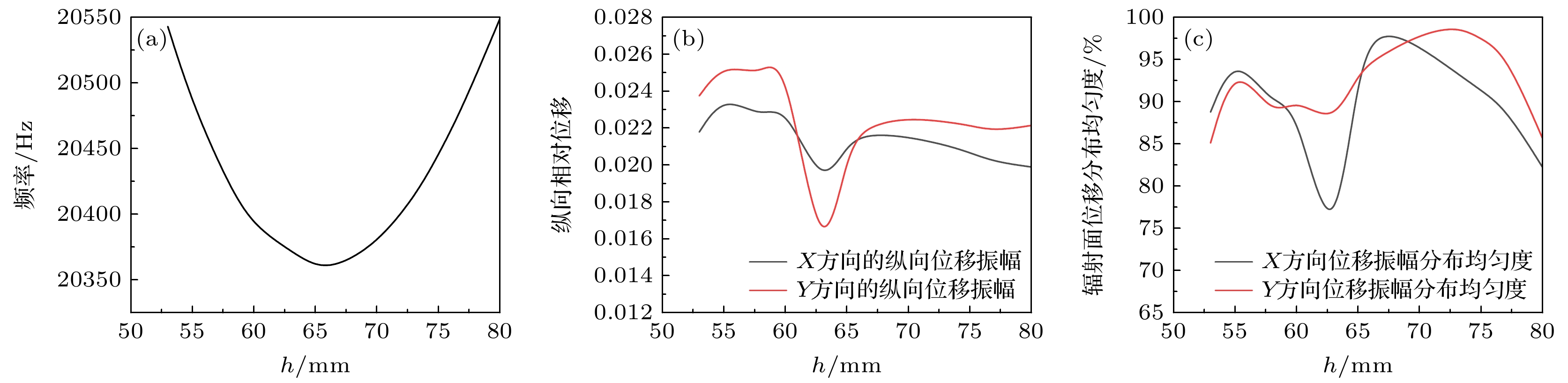
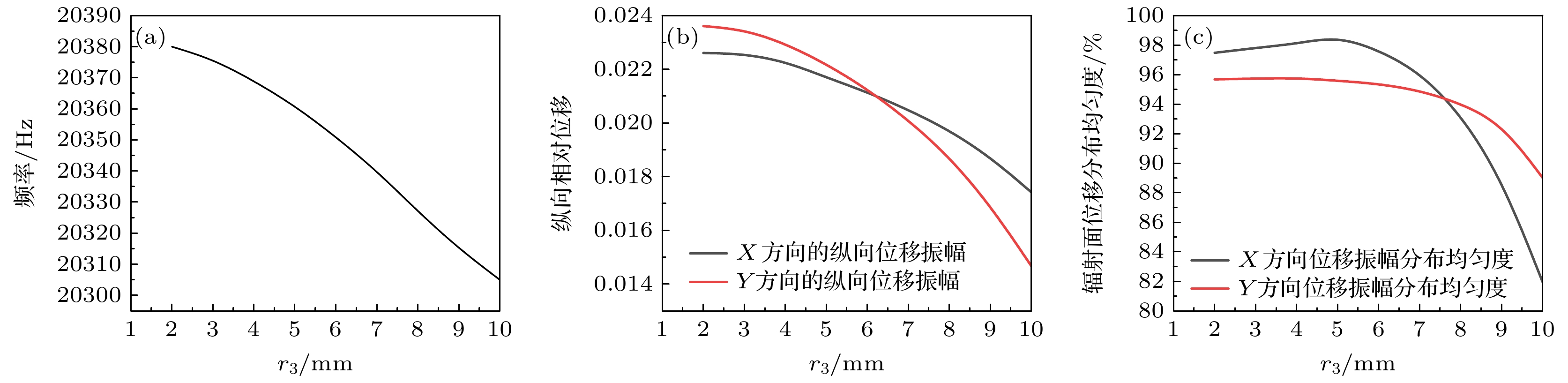
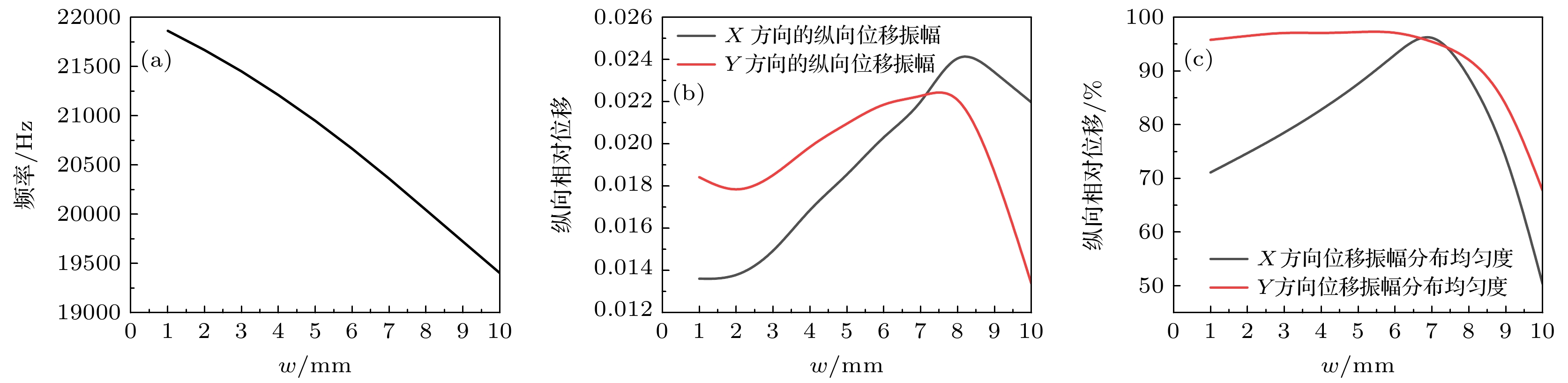
-
对大尺寸三维超声换能器系统的耦合振动进行有效控制, 优化系统的性能, 一直都是功率超声领域亟待解决的难题. 研究发现, 一些声子晶体槽、孔结构可以对大尺寸换能器系统的横向振动进行抑制, 提高系统振幅分布均匀度, 且可以通过改变声子晶体结构的配置参数人为地实现对大尺寸三维超声振动系统性能的调控. 但过多的设计参数必然会增加系统设计的复杂度, 且目前大尺寸三维超声换能器系统的优化设计依赖于经验试错法, 设计效率和成功率较低, 性能也无法保证. 研究引入同质位错、点缺陷结构对大尺寸三维超声振动系统进行优化设计, 并利用数据分析技术评价了同质位错、点缺陷结构的配置对系统辐射面的纵向位移振幅、振幅分布均匀度、辐射声功率、工作带宽等的影响规律, 建立了同质位错结构、近周期缺陷结构的结构参数——大尺寸超声换能器系统性能的预测模型, 实现了对大尺寸功率超声换能器系统的智能设计, 提高了设计效率和成功率, 降低了设计成本.
-
关键词:
- 耦合振动 /
- 大尺寸三维超声振动系统 /
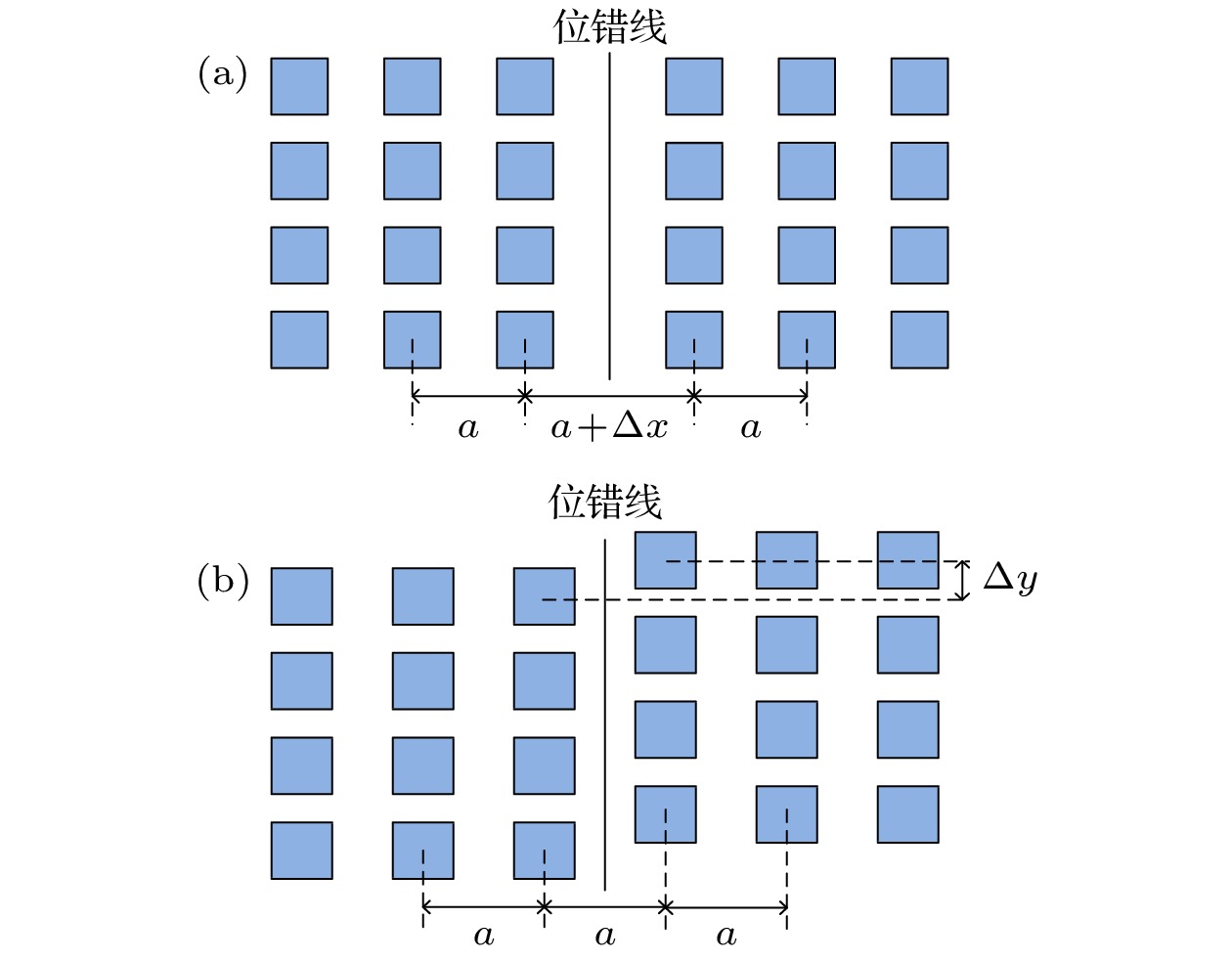
- 同质位错 /
- 点缺陷 /
- 智能化设计
Large-scale three-dimensional ultrasonic vibration systems are susceptible to the influence of coupled vibration, resulting in a series of problems such as increased energy loss, small longitudinal displacement amplitude of the radiation surface, and uneven distribution of longitudinal displacement amplitude, which can seriously affect the working efficiency of ultrasonic processing system. How to effectively control the coupled vibration of large-scale three-dimensional ultrasonic transducer systems and optimize their performance has become an urgent problem in the field of power ultrasound. The research has found that some phononic crystal slots and point defect structures can suppress the lateral vibration of large-scale transducer systems, improve the uniformity of system amplitude distribution, and artificially regulate the performance of large-scale three-dimensional ultrasonic vibration systems by changing the configuration parameters of phononic crystal structures. However, excessive design parameters will inevitably increase the complexity of system design, and, currently, the optimization design of large-scale three-dimensional ultrasonic transducer systems relies on empirical trial and error methods which has low design efficiency and low success rate, and cannot guarantee the system performance. Therefore, in the study, homogeneous dislocations and point defect structures are introduced to optimize the design of large-scale three-dimensional ultrasonic vibration systems. Data analysis techniques are used to evaluate the influences of the configuration of homogeneous dislocations and point defect structures on the longitudinal displacement amplitude, amplitude distribution uniformity, radiated sound power, working bandwidth of the system’s radiation surface. And a predictive model for the performance of large-scale ultrasonic transducer system with homogeneous dislocation structure and near periodic defect structure is established, which can achieve intelligent design of large-scale power ultrasonic transducer system, improve design efficiency and success rate, and reduce the design cost.-
Keywords:
- coupled vibration /
- large-scale three-dimensional ultrasonic vibration system /
- homogeneous dislocations /
- point defects /
- intelligent design
[1] 周光平, 梁明军, 王家宣 2004 声学技术 2004 183
Google Scholar
Zhou G P, Liang M J, Wang J X 2004 Tech. Acous. 2004 183
Google Scholar
[2] Mori E, Itoh K, Imamura A 1995 J. Acous. Soc. Jpn. 51 455
Google Scholar
[3] Lin S 1995 Appl. Acous. 44 249
Google Scholar
[4] Ren S C 1983 Acta Acus. 1 152
Google Scholar
[5] Lin S 2009 IEEE Trans. Ultra. Ferr. Freq Cont. 56 1990.
Google Scholar
[6] 俞宏沛 1994 声学与电子工程 1994 9
Yu H P 1994 Acous. Elec. Engi. 1994 9
[7] 周利生 1993 声学与电子工程 1993 28
Zhou L S 1993 Acous. Elec. Engi. 1993 28
[8] 周利生 1993 声学与电子工程 1993 16
Zhou L S 1993 Acous. Elec. Engi. 1993 16
[9] 林书玉, 张福成 1992 声学学报 1992 451
Lin S Y, Zhang F C 1991 J. Acous. 1992 451
[10] 林书玉, 张福成 1991 应用声学 1991 10
Google Scholar
Lin S Y, Zhang F C 1991 Appl. Acous. 1991 10
Google Scholar
[11] 林书玉, 张福成, 郭孝武 1991 声学学报 1991 91
Google Scholar
Lin S Y, Zhang F C Guo X W 1991 J. Acous. 1991 91
Google Scholar
[12] Lucas M, Smith A C 1997 J. Vibr. Acous. 119 410
Google Scholar
[13] Cardoni A, Lucas M 2002 Ultrasonics 40 365
Google Scholar
[14] Kumar R D, Rani M R, Elangovan S 2014 Appl. Mech. Mater. 592-594 859
Google Scholar
[15] Yeon J L, Muhammad B S, Dong S P 2019 MATEC Web Conf. 257 1
Google Scholar
[16] Adachi K, Ueha S 1990 J. Acous. Soc. Am. 87 208
Google Scholar
[17] Thanh H N, Quang T Q, Cong L T 2017 IOP Conference Series:Materials Science and Engineering 241 1
Google Scholar
[18] Rani M R, Prakasan K, Rudramoorthy R 2014 Int. J. Des. 5 344
Google Scholar
[19] 程存弟 1991 应用声学 10 44
Google Scholar
Chen C D 1991 Appl. Acous. 10 44
Google Scholar
[20] 林书玉, 张福成 1992 声学技术 11 24
Google Scholar
Lin S Y, Zhang F C 1992 Tech. Acous. 11 24
Google Scholar
[21] 梁召峰, 周光平, 莫喜平, 张亦慧, 李正中 2008 机械科学与技术 27 334
Google Scholar
Liang Z F, Zhou G P, Mo X P, Zhang Y H, Li Z Z 2008 Mech. Sci. Tech. 27 334
Google Scholar
[22] 梁召峰, 周光平, 莫喜平, 李正中 2009 工程设计学报 16 200
Google Scholar
Liang Z F, Zhou G P, Mo X P, Zhang Y H, Li Z Z 2009 Journal of Engineering Design 16 200
Google Scholar
[23] 成桢, 郭建中 2010 声学技术 29 103
Chen Z, Guo J Z 2010 Tech. Acous. 29 103
[24] 赵甜甜, 林书玉, 段祎林 2018 67 024303
Google Scholar
Zhao T T, Lin S Y, Duan Y L 2018 Acta Phys. Sin. 67 024303
Google Scholar
[25] 王莎, 林书玉 2019 68 173
Google Scholar
Wang S, Lin S Y 2019 Acta Phys. Sin. 68 173
Google Scholar
[26] Wang S, Lin S Y 2019 Ultrasonics 99 105954.
Google Scholar
[27] Lin J Y, Lin S Y 2020 Crystals 10 1
Google Scholar
[28] Zhao Y C, Zhao F, Yuan L B 2006 J. Harbin Eng. Univ. 2006 617 [赵言诚, 赵芳, 苑立波 2006 哈尔滨工程大学学报 2006 617]
Google Scholar
Zhao Y C, Zhao F, Yuan L B 2006 J. Harbin Eng. Univ. 2006 617
Google Scholar
[29] Zhao F, Wan L B 2006 Acta Phys. Sin. 2 517 [赵芳, 苑立波 2006 2 517]
Google Scholar
Zhao F, Wan L B 2006 Acta Phys. Sin. 2 517
Google Scholar
[30] 何姣 2013 博士学位论文 (昆明: 云南师范大学)
He J 2013 Ph. D. Dissertation (Kunming: Yunnan Normal University
[31] 魏琦, 程营, 刘晓峻 2011 60 124301
Google Scholar
Wei Q, Cheng Y, Liu X J 2011 Acta Phys. Sin. 60 124301
Google Scholar
-
图 1 大尺寸三维长方体超声振动系统结构示意图及中心线位置
Fig. 1. Structural schematic diagram and centerline position of large-dimension 3D cube ultrasonic vibration system.
图 2 大尺寸三维超声振动系统振型图
Fig. 2. Modal diagram of large-dimension 3D ultrasonic vibration system.
图 3 辐射面和辐射面长度(X方向)和宽度(Y方向)上的纵向相对位移振幅分布对比图
Fig. 3. Comparison diagram of longitudinal relative displacement amplitude distribution on the radiation surface and the length (X-direction) and width (Y-direction) of the radiation surface.
图 4 同质位错结构 (a) 横向位错结构; (b) 纵向位错结构
Fig. 4. Schematic diagram of dislocation defect: (a) Lateral dislocation structure; (b) longitudinal dislocation structure.
图 5 同质位错结构的工具头 (a) 模型图; (b) 工具头YZ面的各部分尺寸; (c) 工具头XZ面的各部分尺寸
Fig. 5. Tool heads with homogeneous dislocation structures: (a) Model diagram; (b) dimensions of each part of the YZ surface of the tool head; (c) dimensions of each part of the XZ surface of the tool head.
图 6 同质位错结构的大尺寸三维超声振动系统振型图
Fig. 6. Modal diagram of large-dimension 3D ultrasonic vibration system with homogeneous dislocation structure.
图 7 辐射面和辐射面长度(X方向)和宽度(Y方向)上的纵向相对位移振幅分布对比图
Fig. 7. Comparison diagram of longitudinal relative displacement amplitude distribution on the radiation surface and the length (X-direction) and width (Y-direction) of the radiation surface.
图 8 同质位错与点缺陷结构的工具头 (a) 模型图; (b) 空气圆椎体孔的尺寸; (c) 空气圆柱体孔的尺寸
Fig. 8. Tool heads with homogeneous dislocations and point defect structures: (a) Model diagram; (b) dimensions of air circular vertebral hole; (c) dimensions of air cylinder holes.
图 9 同质位错与点缺陷结构的大尺寸三维超声振动系统振型图
Fig. 9. Modal diagram of large-dimension 3D ultrasonic vibration system with homogeneous dislocations and point defect structures.
图 10 辐射面和辐射面长度(X方向)和宽度(Y方向)上的纵向相对位移振幅分布对比图
Fig. 10. Comparison diagram of longitudinal relative displacement amplitude distribution on the radiation surface and the length (X-direction) and width (Y-direction) of the radiation surface.
图 11 h对系统性能的影响
Fig. 11. Influence of the parameter of h on the performance of the system.
图 14 r3对系统性能的影响
Fig. 14. Influence of the parameter of r3 on the performance of the system.
图 12 w对系统性能的影响
Fig. 12. Influence of the parameter of w on the performance of the system.
图 13 h1对系统性能的影响
Fig. 13. Influence of the parameter of h1 on the performance of the system.
图 15 频率f的预测值和实测值的对比及相对误差
Fig. 15. Comparison and relative error between predicted and measured values of frequency f.
图 16 x位移的预测值和实测值的对比及相对误差
Fig. 16. Comparison and relative error between predicted and measured values of x displacement.
图 17 y位移的预测值和实测值的对比及相对误差
Fig. 17. Comparison and relative error between predicted and measured values of y displacement.
图 18 x均匀度的预测值和实测值的对比及相对误差
Fig. 18. Comparison and relative error between predicted and measured values of x uniformity.
图 19 y均匀度的预测值和实测值的对比及相对误差
Fig. 19. Comparison and relative error between predicted and measured values of y uniformity.
图 21 未优化系统的输入电阻抗与谐振频率的测量与对比 (a) 测量过程; (b) 测量结果; (c) 仿真导纳曲线图
Fig. 21. Measurement and comparison of input impedance and resonant frequency of unoptimized systems: (a) Measurement process; (b) measurement results; (c) simulation admittance curve.
图 22 优化后系统的输入电阻抗与谐振频率的测量与对比 (a) 测量过程; (b) 测量结果; (c) 仿真导纳曲线图
Fig. 22. Measurement and comparison of input impedance and resonant frequency of the optimized system: (a) Measurement process; (b) measurement results; (c) simulation admittance curve.
图 23 振幅分布的测量 (a) 测量过程; (b) 未优化系统的测量结果; (c) 优化后系统的测量结果
Fig. 23. Measurement of amplitude distribution: (a) Measurement process; (b) measurement results of non-optimized systems; (c) measurement results of the optimized system.
图 24 加工的两套系统的辐射面位移振幅对比图
Fig. 24. Displacement amplitude comparison diagram of the radiation surface of the two systems processed.
表 1 系统的材料和结构参数表
Table 1. Material and structural parameter table of the system.
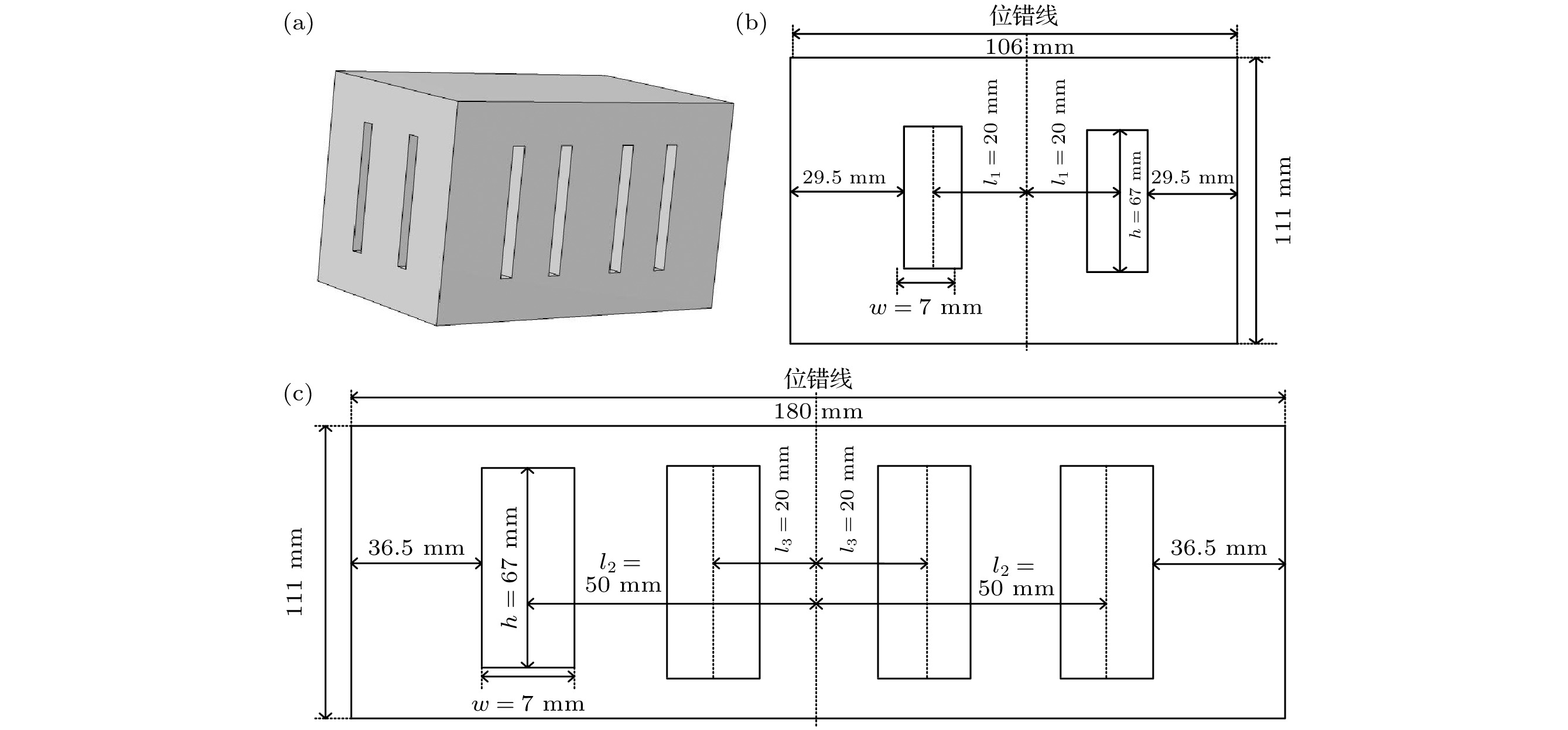
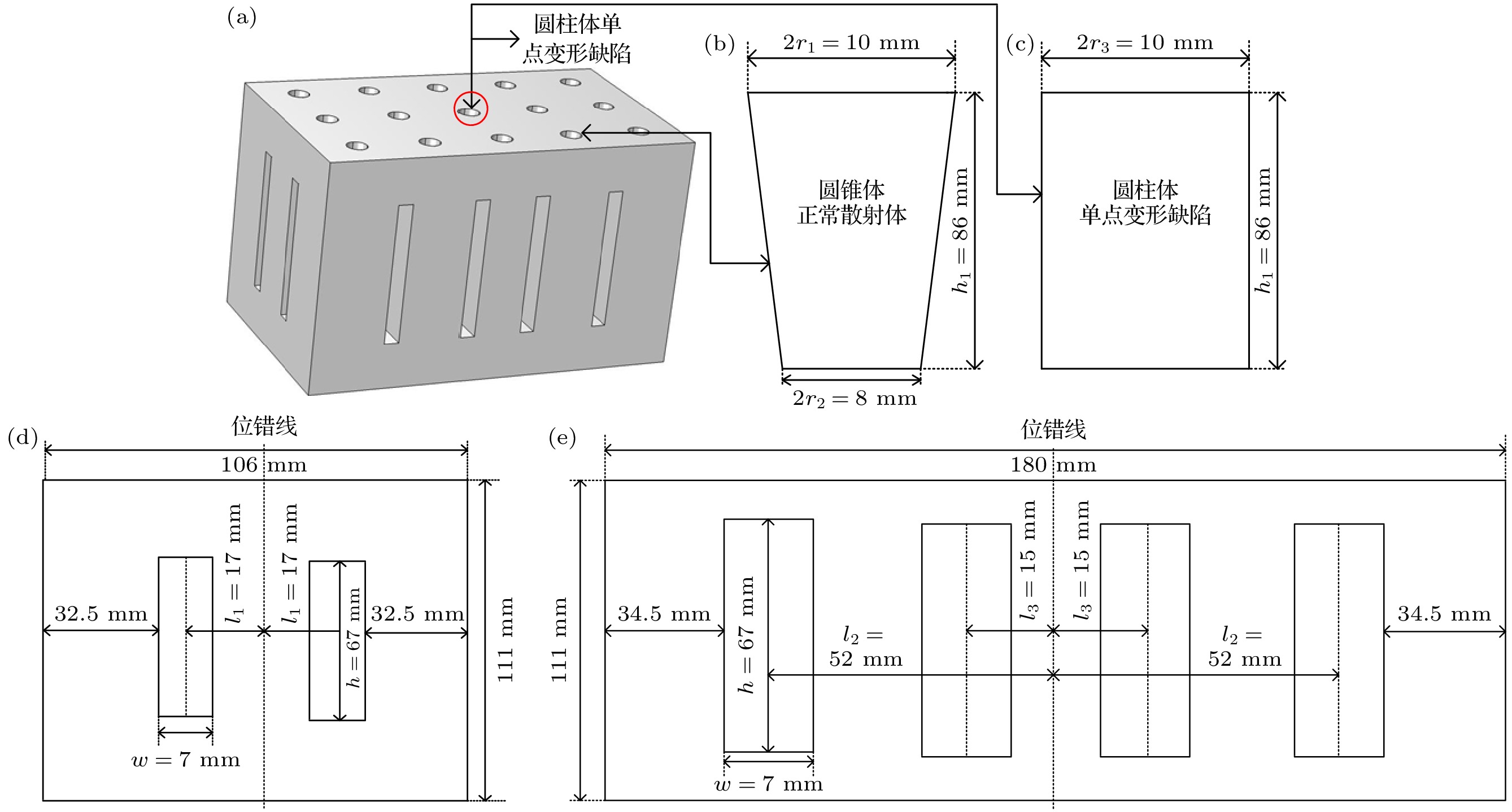
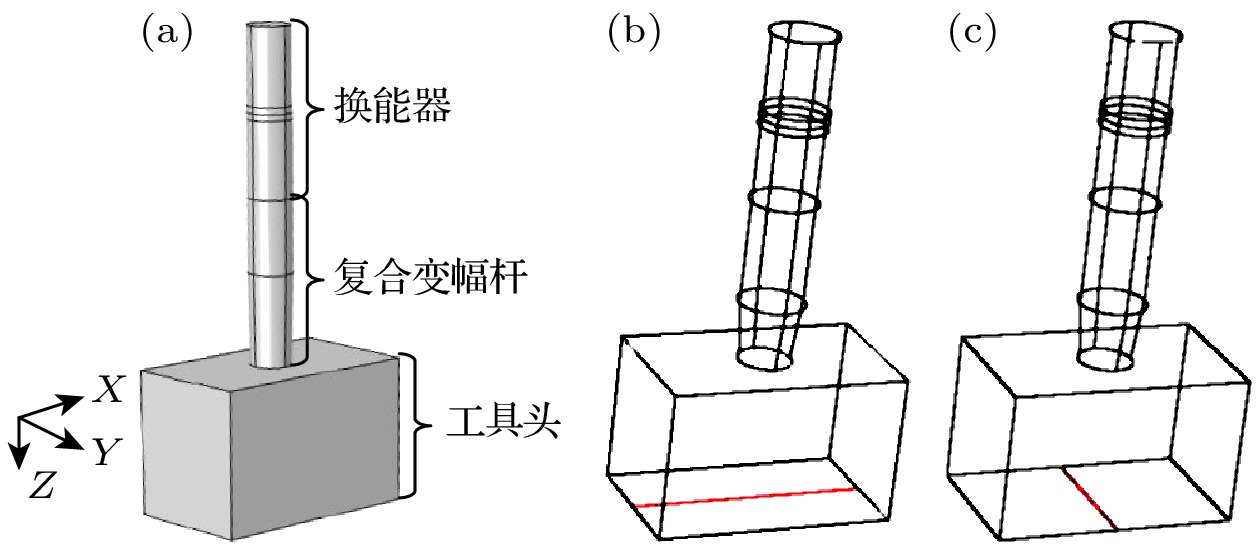
部件 材料属性 形状 大端半径(长)/mm 小端半径(宽)/mm 高度/mm 换能器前盖板 Aluminum 6063-T83 等截面圆柱 25 25 56 换能器压电陶瓷片(两片) PZT-4 等截面圆环 25 25 6 换能器后盖板 Aluminum 6063-T83 等截面圆柱 25 25 56 复合变幅杆圆柱部分 Aluminum 6063-T83 等截面圆柱 25 25 77 复合变幅杆圆锥部分 Aluminum 6063-T83 圆锥 25 20 45 工具头 Aluminum 6063-T83 长方体 180 106 111 
下载: 导出CSV
-
[1] 周光平, 梁明军, 王家宣 2004 声学技术 2004 183
Google Scholar
Zhou G P, Liang M J, Wang J X 2004 Tech. Acous. 2004 183
Google Scholar
[2] Mori E, Itoh K, Imamura A 1995 J. Acous. Soc. Jpn. 51 455
Google Scholar
[3] Lin S 1995 Appl. Acous. 44 249
Google Scholar
[4] Ren S C 1983 Acta Acus. 1 152
Google Scholar
[5] Lin S 2009 IEEE Trans. Ultra. Ferr. Freq Cont. 56 1990.
Google Scholar
[6] 俞宏沛 1994 声学与电子工程 1994 9
Yu H P 1994 Acous. Elec. Engi. 1994 9
[7] 周利生 1993 声学与电子工程 1993 28
Zhou L S 1993 Acous. Elec. Engi. 1993 28
[8] 周利生 1993 声学与电子工程 1993 16
Zhou L S 1993 Acous. Elec. Engi. 1993 16
[9] 林书玉, 张福成 1992 声学学报 1992 451
Lin S Y, Zhang F C 1991 J. Acous. 1992 451
[10] 林书玉, 张福成 1991 应用声学 1991 10
Google Scholar
Lin S Y, Zhang F C 1991 Appl. Acous. 1991 10
Google Scholar
[11] 林书玉, 张福成, 郭孝武 1991 声学学报 1991 91
Google Scholar
Lin S Y, Zhang F C Guo X W 1991 J. Acous. 1991 91
Google Scholar
[12] Lucas M, Smith A C 1997 J. Vibr. Acous. 119 410
Google Scholar
[13] Cardoni A, Lucas M 2002 Ultrasonics 40 365
Google Scholar
[14] Kumar R D, Rani M R, Elangovan S 2014 Appl. Mech. Mater. 592-594 859
Google Scholar
[15] Yeon J L, Muhammad B S, Dong S P 2019 MATEC Web Conf. 257 1
Google Scholar
[16] Adachi K, Ueha S 1990 J. Acous. Soc. Am. 87 208
Google Scholar
[17] Thanh H N, Quang T Q, Cong L T 2017 IOP Conference Series:Materials Science and Engineering 241 1
Google Scholar
[18] Rani M R, Prakasan K, Rudramoorthy R 2014 Int. J. Des. 5 344
Google Scholar
[19] 程存弟 1991 应用声学 10 44
Google Scholar
Chen C D 1991 Appl. Acous. 10 44
Google Scholar
[20] 林书玉, 张福成 1992 声学技术 11 24
Google Scholar
Lin S Y, Zhang F C 1992 Tech. Acous. 11 24
Google Scholar
[21] 梁召峰, 周光平, 莫喜平, 张亦慧, 李正中 2008 机械科学与技术 27 334
Google Scholar
Liang Z F, Zhou G P, Mo X P, Zhang Y H, Li Z Z 2008 Mech. Sci. Tech. 27 334
Google Scholar
[22] 梁召峰, 周光平, 莫喜平, 李正中 2009 工程设计学报 16 200
Google Scholar
Liang Z F, Zhou G P, Mo X P, Zhang Y H, Li Z Z 2009 Journal of Engineering Design 16 200
Google Scholar
[23] 成桢, 郭建中 2010 声学技术 29 103
Chen Z, Guo J Z 2010 Tech. Acous. 29 103
[24] 赵甜甜, 林书玉, 段祎林 2018 67 024303
Google Scholar
Zhao T T, Lin S Y, Duan Y L 2018 Acta Phys. Sin. 67 024303
Google Scholar
[25] 王莎, 林书玉 2019 68 173
Google Scholar
Wang S, Lin S Y 2019 Acta Phys. Sin. 68 173
Google Scholar
[26] Wang S, Lin S Y 2019 Ultrasonics 99 105954.
Google Scholar
[27] Lin J Y, Lin S Y 2020 Crystals 10 1
Google Scholar
[28] Zhao Y C, Zhao F, Yuan L B 2006 J. Harbin Eng. Univ. 2006 617 [赵言诚, 赵芳, 苑立波 2006 哈尔滨工程大学学报 2006 617]
Google Scholar
Zhao Y C, Zhao F, Yuan L B 2006 J. Harbin Eng. Univ. 2006 617
Google Scholar
[29] Zhao F, Wan L B 2006 Acta Phys. Sin. 2 517 [赵芳, 苑立波 2006 2 517]
Google Scholar
Zhao F, Wan L B 2006 Acta Phys. Sin. 2 517
Google Scholar
[30] 何姣 2013 博士学位论文 (昆明: 云南师范大学)
He J 2013 Ph. D. Dissertation (Kunming: Yunnan Normal University
[31] 魏琦, 程营, 刘晓峻 2011 60 124301
Google Scholar
Wei Q, Cheng Y, Liu X J 2011 Acta Phys. Sin. 60 124301
Google Scholar
下载:
计量
- 文章访问数: 1902
- PDF下载量: 63
- 被引次数: 0
