基于亥姆霍兹共振的超薄弧形声学超表面地毯斗篷

隋玉梅; 何兆剑; 毕仁贵; 孔鹏; 吴吉恩; 赵鹤平; 邓科

doi:10.7498/aps.73.20231706

摘要

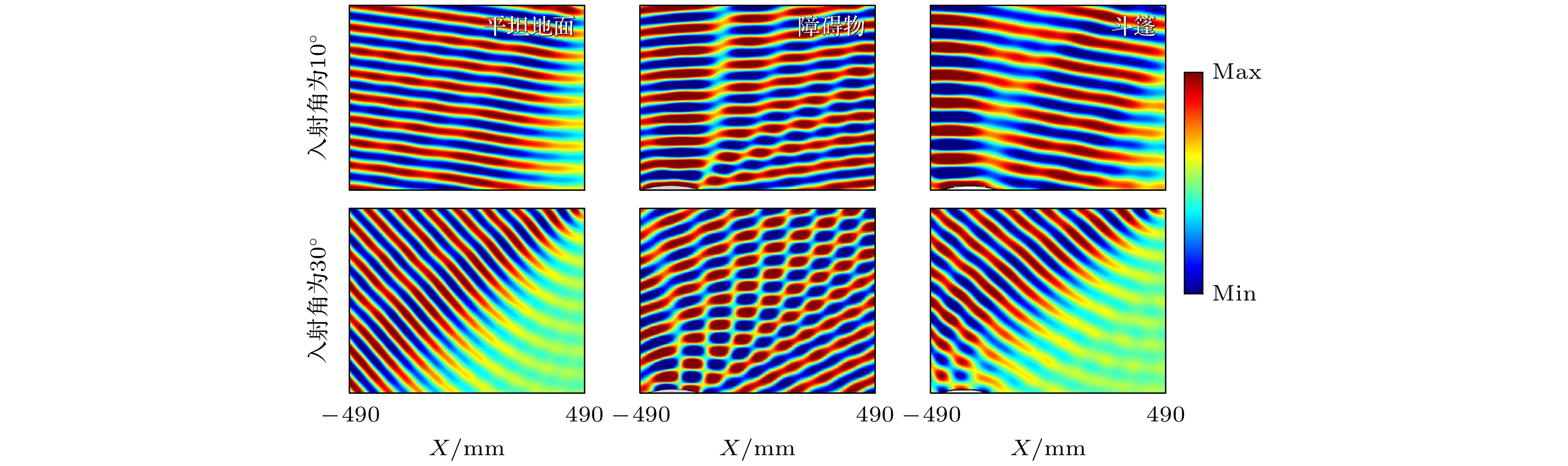
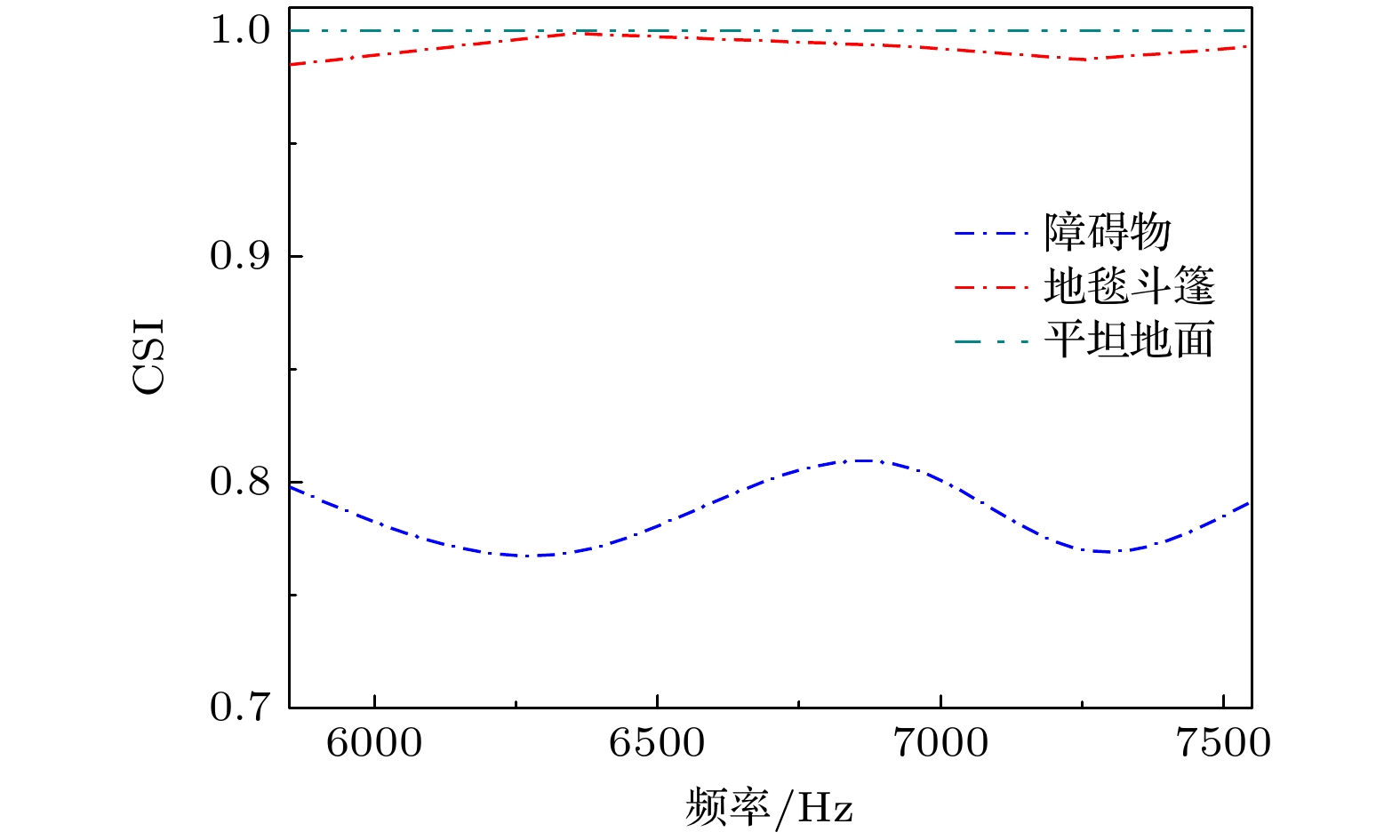
利用局部相位补偿调制的方式设计了一种超薄的弧形声学超表面地毯隐身斗篷. 该斗篷由52个亥姆霍兹空腔共振结构单元组成, 且结构单元厚度小于波长的0.2倍. 数值模拟结果显示: 文中所设计的隐身斗篷在深亚波长范围内隐身效果良好, 其工作频宽为5850—7550 Hz. 进一步探究声波斜入射时地毯斗篷的工作效果, 发现在30°的入射角范围内都具有良好的隐身效果. 此外, 利用余弦相似度(cosine similarity, CSI)函数精确量化分析了该隐身斗篷的工作性能, 计算结果展示, 在斗篷工作的带宽范围内, 覆盖斗篷后的CSI值趋近于无斗篷覆盖地面的CSI值, 展示了其在的良好隐身性. 本文所设计的斗篷均以超薄的亥姆霍兹共振结构为组成单元, 结构简单, 易于实现, 有利于未来的实际应用.

关键词:

Abstract

With the development of metamaterials, the acoustic cloaking has attracted extensive attention due to its novel physics and potential applications. In recent years, based on the phase compensation modulation from Generalized Snell’s law and coordinate transformation, the acoustic cloakings in underwater and air have been widely and deeply studied. However, there is still an urgent need to design acoustic cloaks that are thinner and less affected by the incident angle of acoustic waves. Further, the designed cloaks should have a wider operating band and be more suitable for irregular objects.In this paper, an ultrathin curved acoustic metasurface carpet cloaking is studied by using of phase compensation modulation. The phase modulation is based on Helmholtz resonance (HR). The metasurface carpet is immersed in air, since the vibration mode of acoustic wave in the air is relatively single, thus the physical essence can be elucidated more clearly. The carpet cloak is composed of 52 Helmholtz resonant units, and the size of resonant unit is less than 0.2 of working wavelength.The phase change of HR unit is solved analytically by using the Generalized Snell’s law, and confirmed by the Multiphysics COMSOL software. The parameter effects of HR unit on the phase change are studied, demonstrating that the phase change of HR unit is sensitive to the change of height and radius of HR unit, while the change of width of HR cavity neck can make the phase of HR unit change smoothly. Therefore, when building 52 HR units, the width of the HR cavity neck is designed, and the height and radius of HR unit stay fixed.The simulating results demonstrate that the designed cloak works well in a frequency range from 5850 Hz to 7550 Hz. Also, we study the cloaking effect for oblique incidence, and the results show that the carpet cloak works well for incident angle less than 30°. To quantitatively analyze the bandwidth of the cloaking, we calculate the cosine similarity value. It elucidates that the value of the cloak is very close to that of the flat ground in a corresponding working frequency range. The cloak designed in this work is made of ultrathin Helmholtz Resonant structures. This cloak is simple and easy to realize and conducive to potential applications.

Keywords:

作者及机构信息

1.
湖南科技大学物理与电子科学学院, 智能传感器与新型传感材料湖南省重点实验室, 湘潭　411201

2.
吉首大学物理系, 吉首　416000

3.
湖南财政经济学院, 长沙　410205

通信作者: 何兆剑, hezj@whu.edu.cn ; 孔鹏, kongpeng@jsu.edu.cn ;

基金项目: 国家自然科学基金(批准号: 11964011, 11764016)资助的课题.

Authors and contacts

1.
Key Labratory of Intelligent Sensors and Advanced Sensing Materials of Hunan Province, School of Physics and Electronic Science, Hunan University of Science and Technology, Xiangtan 411021, China

2.
Department of Physics, Jishou University, Jishou 416000, China

3.
Hunan University of Finance and Economics, Changsha 410205, China

Corresponding author: He Zhao-Jian, hezj@whu.edu.cn ; Kong Peng, kongpeng@jsu.edu.cn ;

Funds: Project supported by the National Natural Science Foundation of China (Grant Nos. 11964011, 11764016).

文章全文 : translate this paragraph

参考文献

[1]	Cummer S A, Christensen J, Alù A 2016 Nat. Rev. Mater. 1 16001 Google Scholar
[2]	Lu M H, Feng L, Chen Y F 2009 Mater. Today 12 34 Google Scholar
[3]	Liao G X, Luan C C, Wang Z W, Liu J P, Yao X H, Fu J Z 2021 Adv. Mater. Technol. 6 2000787 Google Scholar
[4]	Zigoneanu L, Popa B I, Cummer S A 2014 Nat. Mater. 13 352 Google Scholar
[5]	Bi Y, Jia H, Sun Z, Yang Y, Zhao H, Yang J 2018 Appl. Phys. Lett. 112 223502 Google Scholar
[6]	Chen H, Chan C T 2007 Appl. Phys. Lett. 91 183518 Google Scholar
[7]	Guild M D, Haberman M R, Alù A 2012 Phys. Rev. B 86 104302 Google Scholar
[8]	Wei Q, Cheng Y, Liu X J 2012 Phys. Rev. B 86 024303 Google Scholar
[9]	Zhou Z, Huang S, Li D, Zhu J, Li Y 2022 Natl. Sci. Rev. 9 nwab171 Google Scholar
[10]	Zhang Y, Tong Y 2021 Opt. Commun. 483 126590 Google Scholar
[11]	Bi Y, Jia H, Lu W, Ji P, Yang J 2017 Sci. Rep. 7 1 Google Scholar
[12]	Chen Y, Zheng M, Liu X, Bi Y, Sun Z, Xiang P, Yang J, Hu G 2017 Phys. Rev. B 95 180104 Google Scholar
[13]	Sun Z, Sun X, Jia H, Bi Y, Yang J 2019 Appl. Phys. Lett. 114 094101 Google Scholar
[14]	Hu W, Fan Y, Ji P, Yang J 2013 J. Appl. Phys. 113 024911 Google Scholar
[15]	Zhang S, Xia C, Fang N 2011 Phys. Rev. Lett. 106 024301 Google Scholar
[16]	Chen Y, Liu X, Hu G 2015 Sci. Rep. 5 15745 Google Scholar
[17]	Guo J, Fang Y, Qu R, Zhang X 2023 Mater. Today 66 321 Google Scholar
[18]	Ji W Q, Wei Q, Zhu X F, Wu D J 2019 J. Phys. D: Appl. Phys. 52 325302 Google Scholar
[19]	Jiang Z, Liang Q, Li Z, Chen T, Li D, Hao Y 2020 Adv. Opt. Mater. 8 2000827 Google Scholar
[20]	Díaz-Rubio A, Tretyakov S A 2017 Phys. Rev. B 96 125409 Google Scholar
[21]	Li X S, Wang Y F, Chen A L, Wang Y S 2020 J. Phys. D: Appl. Phys. 53 195301 Google Scholar
[22]	Zhang H, He J, Liu C, Ma F 2023 Appl. Acoust. 213 109639 Google Scholar
[23]	Tian Y, Wei Q, Cheng Y, Xu Z, Liu X 2015 Appl. Phys. Lett. 107 221906 Google Scholar
[24]	Tang K, Qiu C, Ke M, Lu J, Ye Y, Liu Z 2015 Sci. Rep. 4 6517 Google Scholar
[25]	Faure C, Richoux O, Félix S, Pagneux V 2016 Appl. Phys. Lett. 108 064103 Google Scholar
[26]	Zhu Y, Assouar B 2019 Phys. Rev. B 99 174109 Google Scholar
[27]	Zhou H T, Fan S W, Li X S, Fu W X, Wang Y F, Wang Y S 2020 Smart Mater. Struct. 29 065016 Google Scholar
[28]	He J, Liang Q, Lv P, Wu Y, Chen T 2022 Appl. Acoust. 197 108957 Google Scholar
[29]	Zhou H T, Fu W X, Wang Y F, Wang Y S, Laude V, Zhang C 2021 Mater. Des. 199 109414 Google Scholar
[30]	Wang Y, Cheng Y, Liu X 2019 Sci. Rep. 9 1 Google Scholar
[31]	Zhu Y, Fan X, Liang B, Cheng J, Jing Y 2017 Phys. Rev. X 7 021034 Google Scholar
[32]	Yu G, Qiu Y, Li Y, Wang X, Wang N 2021 Phys. Rev. Appl. 15 064064 Google Scholar
[33]	Guo J, Zhou J 2020 J. Phys. D: Appl. Phys. 53 505501 Google Scholar
[34]	Ji G, Huber J 2022 Appl. Mater. Today 26 101260 Google Scholar
[35]	Zhu Y, Hu J, Fan X, Yang J, Liang B, Zhu X, Cheng J 2018 Nat. Commun. 9 1632 Google Scholar
[36]	Zhou P, Jia H, Bi Y, Liao B, Yang Y, Yan K, Zhang J, Yang J 2022 Phys. Rev. Appl. 18 014050 Google Scholar

施引文献

图 1 利用反射波波前操纵的二维声学超表面地毯隐身示意图　(a)平坦地面; (b) 任意弯曲表面

Fig. 1. Illustration of a 2D acoustic carpet cloaking metasurface for reflected wavefront manipulation: (a) Flat surface; (b) arbitrary curved surface.

下载: 全尺寸图片幻灯片

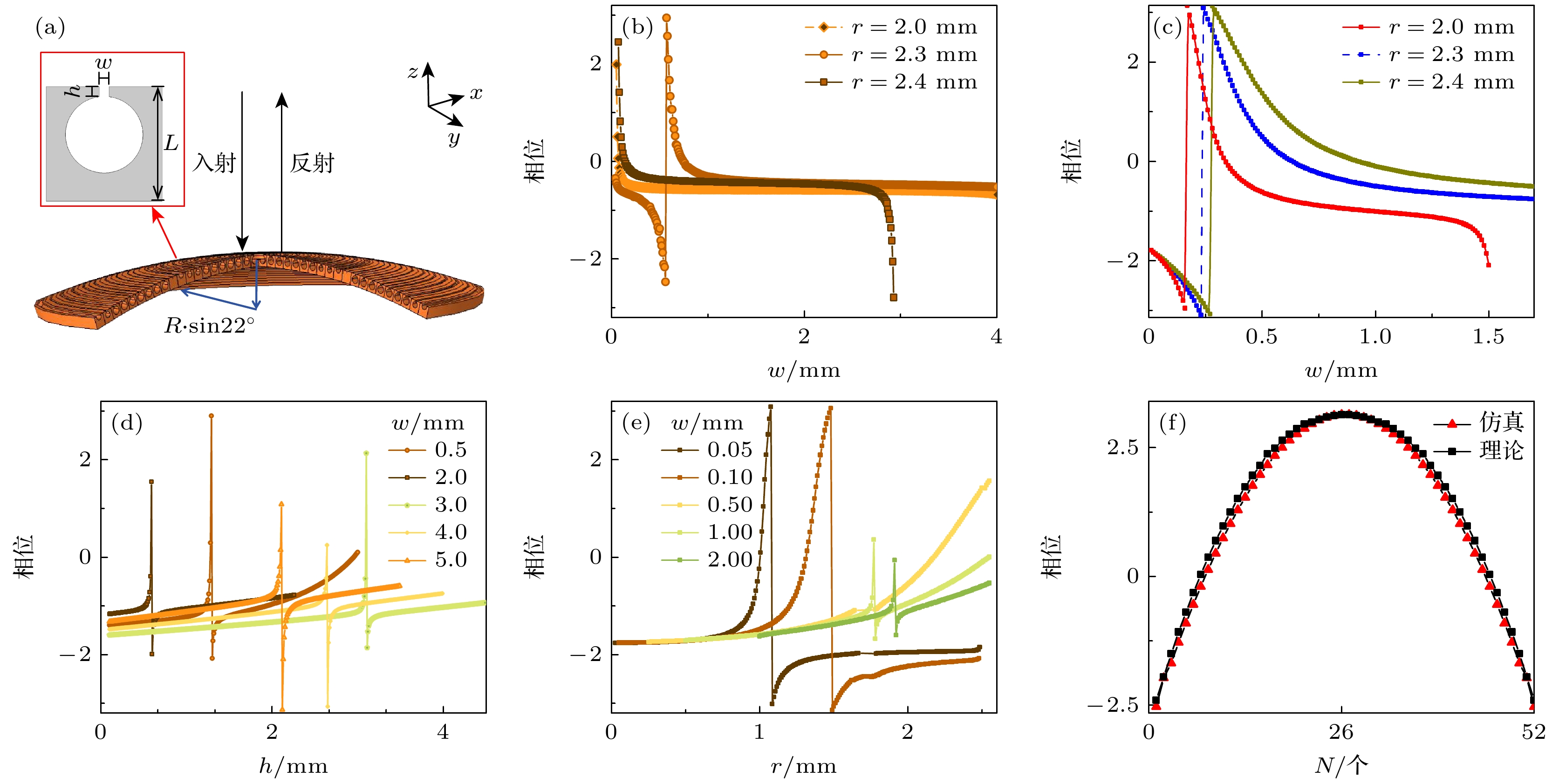
图 2 (a)地毯隐身超表面示意图, 弧形隐身斗篷及斗篷单个共振单元结构(红色框插图), 入射波从–z方向入射; (b), (c) 共振腔中r取不同值时单个共振单元反射相位随w的变化, 其中(b)入射波频率为3430 Hz, (c)入射波频率为6860 Hz; (d)共振腔中w取不同值时单个共振单元反射相位随h的变化; (e)共振腔中w取不同值时单个共振单元反射相位随r的变化; (f) 入射波频率为6860 Hz时, 弧形隐身斗篷中每个共振单元的反射相位(红色曲线)和由(5)式理论计算的相位(黑色曲线)

Fig. 2. (a) Schematic sketch of the metasurface for carpet cloaking, the illustration of arc-shaped carpet cloak, inset showing the schematic diagram of the unit-cell for the carpet. The acoustic waves are incident from –z direction. The reflection phase of single HR unit varing with w for acoustic waves normal incidence with different frequency: (b) 3430 Hz; (c) 6860 Hz. For different w, the reflection phase of single HR unit varing with h (d) and varing with r (e) for acoustic waves normal incidence with frequence 6860 Hz. (f) The reflection phase of each HR unit in the designed AMCC (red curve) and that of theoretical calculation from Eq. (5) (black curve) for acoustic waves normal incidence with frequence 6860 Hz.

下载: 全尺寸图片幻灯片

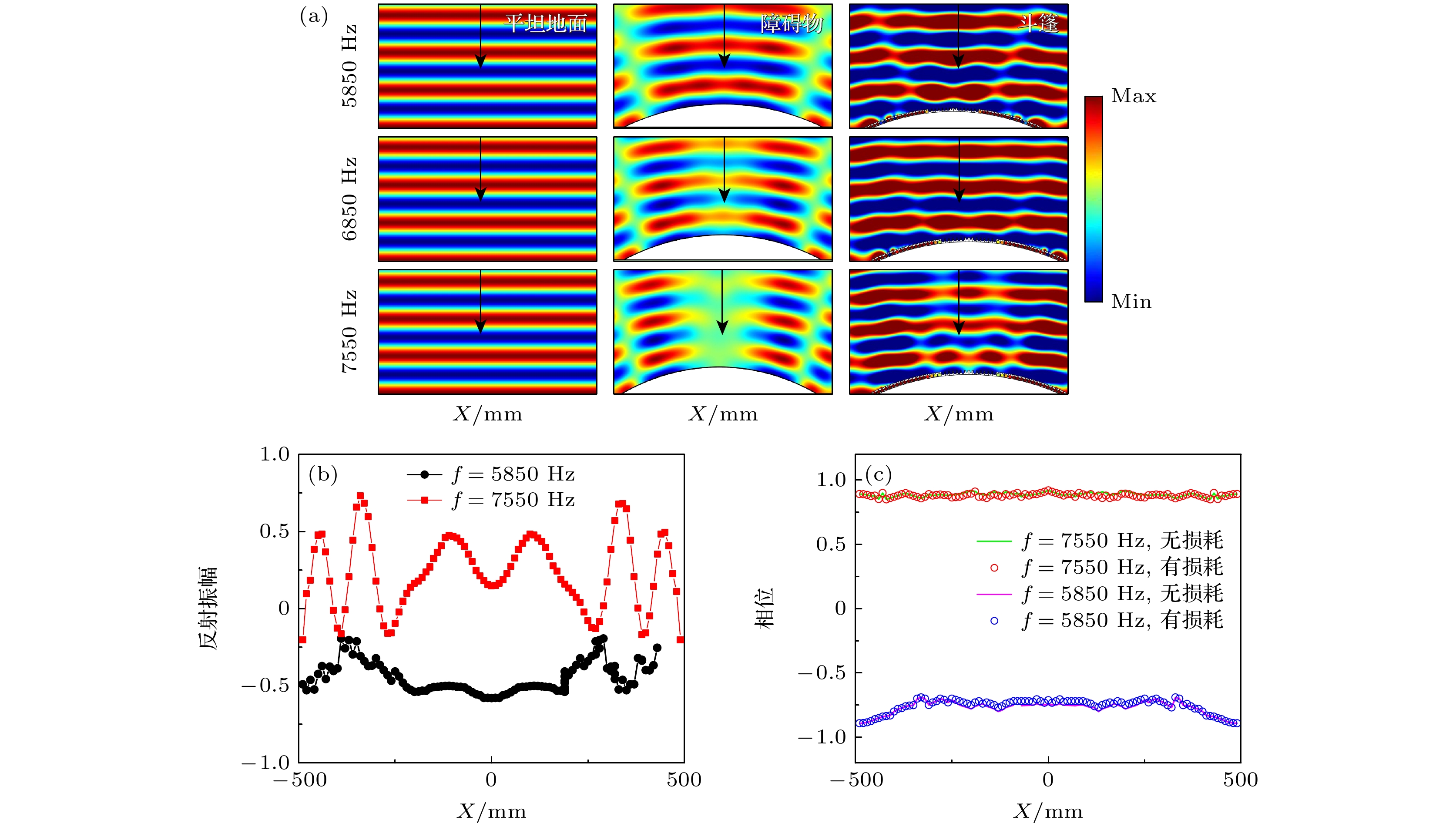
图 3 (a)平面波分别垂直入射至平坦地面、弧形障碍物及覆盖于弧形障碍物上的斗篷时的反射声压场分布; (b) 5850, 7550 Hz频率下Z = 800 mm时归一化反射振幅; (c) 5850, 7550 Hz频率下Z = 800 mm时反射波阵面相位

Fig. 3. (a) Reflected pressure field distributions for a plane wave impinging on the flat ground, the arc-shaped object and the arc-shaped cloak; the normalized reflection amplitudes (b) and reflected wavefront phases (c) which located at Z = 800 mm for the incident frequency 5850 Hz and 7550 Hz.

下载: 全尺寸图片幻灯片

图 4 平面波分别以10°和30°入射角斜入射至平坦地面、弧形障碍物及覆盖于弧形障碍物上的斗篷时的反射声压场分布

Fig. 4. When the incident angles are 10° and 30°, the reflected pressure field distributions for a plane wave impinging on the flat ground, the arc-shaped object and the arc-shaped cloak.

下载: 全尺寸图片幻灯片

图 5 反射声波通过平坦地面、隐身斗篷和障碍物的CSI值

Fig. 5. The CSI of reflected acoustic waves for flat ground, carpet cloak, and arc-shaped object.

下载: 全尺寸图片幻灯片

表 1 隐身斗篷每个共振单元颈宽w和半径r参数表

Table 1. Parameter list of neck width w and radii r of resonant unit in the cloak.

序号	w/mm	r/mm	序号	w/mm	r/mm
1	2.920	1.5	14	0.380	2.4
2	4.455	2.4	15	0.426	2.4
3	4.457	2.4	16	0.472	2.4
4	4.458	2.4	17	0.520	2.4
5	4.459	2.4	18	0.531	2.4
6	4.461	2.4	19	0.621	2.4
7	4.462	2.4	20	0.685	2.4
8	0.060	2.4	21	0.755	2.4
9	0.119	2.4	22	0.852	2.4
10	0.177	2.4	23	0.980	2.4
11	0.233	2.4	24	1.234	2.4
12	0.286	2.4	25	1.574	2.4
13	0.377	2.4	26	3.749	2.4

下载: 导出CSV

map

[1]	Cummer S A, Christensen J, Alù A 2016 Nat. Rev. Mater. 1 16001 Google Scholar
[2]	Lu M H, Feng L, Chen Y F 2009 Mater. Today 12 34 Google Scholar
[3]	Liao G X, Luan C C, Wang Z W, Liu J P, Yao X H, Fu J Z 2021 Adv. Mater. Technol. 6 2000787 Google Scholar
[4]	Zigoneanu L, Popa B I, Cummer S A 2014 Nat. Mater. 13 352 Google Scholar
[5]	Bi Y, Jia H, Sun Z, Yang Y, Zhao H, Yang J 2018 Appl. Phys. Lett. 112 223502 Google Scholar
[6]	Chen H, Chan C T 2007 Appl. Phys. Lett. 91 183518 Google Scholar
[7]	Guild M D, Haberman M R, Alù A 2012 Phys. Rev. B 86 104302 Google Scholar
[8]	Wei Q, Cheng Y, Liu X J 2012 Phys. Rev. B 86 024303 Google Scholar
[9]	Zhou Z, Huang S, Li D, Zhu J, Li Y 2022 Natl. Sci. Rev. 9 nwab171 Google Scholar
[10]	Zhang Y, Tong Y 2021 Opt. Commun. 483 126590 Google Scholar
[11]	Bi Y, Jia H, Lu W, Ji P, Yang J 2017 Sci. Rep. 7 1 Google Scholar
[12]	Chen Y, Zheng M, Liu X, Bi Y, Sun Z, Xiang P, Yang J, Hu G 2017 Phys. Rev. B 95 180104 Google Scholar
[13]	Sun Z, Sun X, Jia H, Bi Y, Yang J 2019 Appl. Phys. Lett. 114 094101 Google Scholar
[14]	Hu W, Fan Y, Ji P, Yang J 2013 J. Appl. Phys. 113 024911 Google Scholar
[15]	Zhang S, Xia C, Fang N 2011 Phys. Rev. Lett. 106 024301 Google Scholar
[16]	Chen Y, Liu X, Hu G 2015 Sci. Rep. 5 15745 Google Scholar
[17]	Guo J, Fang Y, Qu R, Zhang X 2023 Mater. Today 66 321 Google Scholar
[18]	Ji W Q, Wei Q, Zhu X F, Wu D J 2019 J. Phys. D: Appl. Phys. 52 325302 Google Scholar
[19]	Jiang Z, Liang Q, Li Z, Chen T, Li D, Hao Y 2020 Adv. Opt. Mater. 8 2000827 Google Scholar
[20]	Díaz-Rubio A, Tretyakov S A 2017 Phys. Rev. B 96 125409 Google Scholar
[21]	Li X S, Wang Y F, Chen A L, Wang Y S 2020 J. Phys. D: Appl. Phys. 53 195301 Google Scholar
[22]	Zhang H, He J, Liu C, Ma F 2023 Appl. Acoust. 213 109639 Google Scholar
[23]	Tian Y, Wei Q, Cheng Y, Xu Z, Liu X 2015 Appl. Phys. Lett. 107 221906 Google Scholar
[24]	Tang K, Qiu C, Ke M, Lu J, Ye Y, Liu Z 2015 Sci. Rep. 4 6517 Google Scholar
[25]	Faure C, Richoux O, Félix S, Pagneux V 2016 Appl. Phys. Lett. 108 064103 Google Scholar
[26]	Zhu Y, Assouar B 2019 Phys. Rev. B 99 174109 Google Scholar
[27]	Zhou H T, Fan S W, Li X S, Fu W X, Wang Y F, Wang Y S 2020 Smart Mater. Struct. 29 065016 Google Scholar
[28]	He J, Liang Q, Lv P, Wu Y, Chen T 2022 Appl. Acoust. 197 108957 Google Scholar
[29]	Zhou H T, Fu W X, Wang Y F, Wang Y S, Laude V, Zhang C 2021 Mater. Des. 199 109414 Google Scholar
[30]	Wang Y, Cheng Y, Liu X 2019 Sci. Rep. 9 1 Google Scholar
[31]	Zhu Y, Fan X, Liang B, Cheng J, Jing Y 2017 Phys. Rev. X 7 021034 Google Scholar
[32]	Yu G, Qiu Y, Li Y, Wang X, Wang N 2021 Phys. Rev. Appl. 15 064064 Google Scholar
[33]	Guo J, Zhou J 2020 J. Phys. D: Appl. Phys. 53 505501 Google Scholar
[34]	Ji G, Huber J 2022 Appl. Mater. Today 26 101260 Google Scholar
[35]	Zhu Y, Hu J, Fan X, Yang J, Liang B, Zhu X, Cheng J 2018 Nat. Commun. 9 1632 Google Scholar
[36]	Zhou P, Jia H, Bi Y, Liao B, Yang Y, Yan K, Zhang J, Yang J 2022 Phys. Rev. Appl. 18 014050 Google Scholar

[1]	白宇, 张振方, 杨海滨, 蔡力, 郁殿龙. 基于非对称吸声器的发动机声学超表面声衬. , 2023, 72(5): 054301. doi: 10.7498/aps.72.20222011
[2]	杨东如, 程用志, 罗辉, 陈浮, 李享成. 基于双开缝环结构的半反射和半透射超宽带超薄双偏振太赫兹超表面. , 2023, 72(15): 158701. doi: 10.7498/aps.72.20230471
[3]	龙洁, 李九生. 相变材料与超表面复合结构太赫兹移相器. , 2021, 70(7): 074201. doi: 10.7498/aps.70.20201495
[4]	殷允桥, 吴宏伟. 基于人工表面等离激元结构的超表面磁镜. , 2020, 69(23): 234101. doi: 10.7498/aps.69.20200514
[5]	李鑫, 吴立祥, 杨元杰. 矩形纳米狭缝超表面结构的近场增强聚焦调控. , 2019, 68(18): 187103. doi: 10.7498/aps.68.20190728
[6]	杨鹏, 秦晋, 徐进, 韩天成. 超薄柔性透射型超构材料吸收器. , 2019, 68(8): 087802. doi: 10.7498/aps.68.20182225
[7]	丁昌林, 董仪宝, 赵晓鹏. 声学超材料与超表面研究进展. , 2018, 67(19): 194301. doi: 10.7498/aps.67.20180963
[8]	张永燕, 吴九汇, 钟宏民. 新型负模量声学超结构的低频宽带机理研究. , 2017, 66(9): 094301. doi: 10.7498/aps.66.094301
[9]	侯海生, 王光明, 李海鹏, 蔡通, 郭文龙. 超薄宽带平面聚焦超表面及其在高增益天线中的应用. , 2016, 65(2): 027701. doi: 10.7498/aps.65.027701
[10]	郭文龙, 王光明, 李海鹏, 侯海生. 单层超薄高效圆极化超表面透镜. , 2016, 65(7): 074101. doi: 10.7498/aps.65.074101
[11]	孙彦彦, 韩璐, 史晓玉, 王兆娜, 刘大禾. 用于相位突变界面的广义的反射定律和折射定律. , 2013, 62(10): 104201. doi: 10.7498/aps.62.104201
[12]	程用志, 聂彦, 龚荣洲, 王鲜. 基于电阻膜与分形频率选择表面的超薄宽频带超材料吸波体的设计. , 2013, 62(4): 044103. doi: 10.7498/aps.62.044103
[13]	张兆慧, 韩奎, 曹娟, 王帆, 杨丽娟. 有机分子超薄膜的结构对摩擦的影响. , 2012, 61(2): 028701. doi: 10.7498/aps.61.028701
[14]	沈惠杰, 温激鸿, 郁殿龙, 蔡力, 温熙森. 基于主动声学超材料的圆柱声隐身斗篷设计研究. , 2012, 61(13): 134303. doi: 10.7498/aps.61.134303
[15]	丁昌林, 赵晓鹏. 可听声频段的声学超材料. , 2009, 58(9): 6351-6355. doi: 10.7498/aps.58.6351
[16]	孟庆苗, 蒋继建, 刘景伦, 邓德力. 动态Dilaton-Maxwell黑洞的广义Stefan-Boltzmann定律. , 2009, 58(1): 78-82. doi: 10.7498/aps.58.78
[17]	卢亚锋, M.Przybylski, 王文宏, 闫龙, 石一生, J. Barthel. 在Pd/Cu(100)表面上外延的超薄Co膜的结构和磁性. , 2005, 54(11): 5405-5410. doi: 10.7498/aps.54.5405
[18]	段一士, 冯世祥. 广义相对论中广义协变的角动量守恒定律. , 1995, 44(9): 1373-1381. doi: 10.7498/aps.44.1373
[19]	屠礼勋, 孙玉珍. Ga在Ni(111)表面上形成的超结构. , 1985, 34(7): 964-967. doi: 10.7498/aps.34.964
[20]	熊诗杰, 蔡建华. 关于多层超薄共格结构的导电性质. , 1984, 33(3): 352-361. doi: 10.7498/aps.33.352

计量

文章访问数: 1932
PDF下载量: 77
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板