非厄米格点模型的经典电路模拟

徐灿鸿; 许志聪; 周子榆; 成恩宏; 郎利君

doi:10.7498/aps.72.20230914

摘要

量子模拟是研究和理解量子世界中奇异物理现象的重要手段. 近年来, 人们发现除了量子平台, 经典系统 (如光子晶体、声子晶体和机械振子等) 也能通过类比薛定谔方程的方式模拟量子模型. 其中, 经典电路因具有成本低廉、技术成熟和易于扩展等特点, 成为一个新兴的模拟平台, 并成功模拟了许多重要的量子现象. 与此同时, 非厄米物理突破了传统量子力学中系统哈密顿量的厄米性, 为人们理解量子系统, 尤其是开放量子系统中的物理, 提供了一种新的视角. 非厄米系统由于展现出不同于厄米系统的新奇现象, 在物理学的多个领域中成为新兴的研究对象. 然而, 许多非厄米现象所要求的奇异构型在量子平台上实现的技术门槛相对较高, 例如非厄米趋肤效应通常需要系统具备非互易的格点间跃迁. 因此, 利用操控灵活的经典电路模拟非厄米物理成为一种自然的选择. 本文旨在通过简要介绍非厄米物理的相关知识 (包括数学基础和新奇现象) 以及经典电路的模拟理论 (包括对格点模型的映射理论、非厄米的引入和物理量的测量等), 概述当前经典电路模拟非厄米格点模型的实验进展, 为相关研究工作提供参考, 以推动该领域的进一步发展.

关键词:

Abstract

Quantum simulation serves as a significant tool for studying and understanding novel phenomena in the quantum world. In recent years, it has be realized that apart from quantum platforms, classical systems like photonic crystals, phononic crystals, and mechanical oscillators can also be used to simulate quantum models by analogizing the Schrödinger equation. Among these systems, electrical circuits have emerged as a promising simulation platform owing to their low cost, technological maturity, and ease of scalability, successfully simulating numerous important quantum phenomena. Meanwhile, non-Hermitian physics breaks the Hermiticity of systems’ Hamiltonians in traditional quantum mechanics, providing a fresh perspective for understanding the physics of quantum systems, particularly open quantum systems. Non-Hermitian systems, owing to their manifestation of unique phenomena absent in Hermitian systems, have become emerging research subjects in various fields of physics. However, many non-Hermitian phenomena require specialized configurations that pose relatively high technical thresholds on quantum platforms. For instance, the non-Hermitian skin effect typically requires systems to possess non-reciprocal hopping between lattice sites. Therefore, utilizing flexible electrical circuits to simulate non-Hermitian physics becomes a natural choice.This paper provides a short review of the current experimental progress in simulating non-Hermitian lattice models by using electrical circuits. It offers a brief introduction to the relevant knowledge of non-Hermitian physics, including mathematical concepts and novel phenomena, as well as the simulation theory of electrical circuits, including the mapping theory of the lattice models, the introduction of non-Hermiticity, and the measurement of physical quantities. The aim is to provide readers with a reference for better understanding or engagement in related researches, thus promoting further development in this field.

Keywords:

作者及机构信息

1.
华南师范大学物理学院, 广州　510006

2.
华南师范大学, 广东省量子调控工程与材料重点实验室, 广州　510006

通信作者: 成恩宏, ehcheng@m.scnu.edu.cn ; 郎利君, ljlang@scnu.edu.cn

基金项目: 广东省基础与应用基础研究基金 (批准号: 2019A1515111101) 和华南师范大学科研启动基金资助的课题.

Authors and contacts

1.
School of Physics, South China Normal University, Guangzhou 510006, China

2.
Guangdong Provincial Key Laboratory of Quantum Engineering and Quantum Materials, South China Normal University, Guangzhou 510006, China

Corresponding author: Cheng En-Hong, ehcheng@m.scnu.edu.cn ; Lang Li-Jun, ljlang@scnu.edu.cn

Funds: Project supported by the Guangdong Basic and Applied Basic Research Foundation, China (Grant No. 2019A1515111101) and the Startup Funding from South China Normal University, China.

文章全文 : translate this paragraph

参考文献

[1]	Feynman R P 1982 Int. J. Theor. Phys. 21 467 Google Scholar
[2]	Greiner M, Mandel O, Esslinger T, Hänsch T W, Bloch I 2002 Nature 415 39 Google Scholar
[3]	Billy J, Josse V, Zuo Z, Bernard A, Hambrecht B, Lugan P, Clement D, Sanchez-Palencia L, Bouyer P, Aspect A 2008 Nature 453 891 Google Scholar
[4]	Zhang D W, Zhu Y Q, Zhao Y X, Yan H, Zhu S L 2018 Adv. Phys. 67 253 Google Scholar
[5]	Friedenauer A, Schmitz H, Glueckert J T, Porras D, Schaetz T 2008 Nat. Phys. 4 757 Google Scholar
[6]	Barreiro J T, Müller M, Schindler P, Nigg D, Monz T, Chwalla M, Hennrich M, Roos C F, Zoller P, Blatt R 2011 Nature 470 486 Google Scholar
[7]	Blatt R, Roos C F 2012 Nat. Phys. 8 277 Google Scholar
[8]	You J Q, Shi X F, Hu X, Nori F 2010 Phys. Rev. B 81 014505 Google Scholar
[9]	Georgescu I, Ashhab S, Nori F 2014 Rev. Mod. Phys. 86 153 Google Scholar
[10]	Barends R, Kelly J, Megrant A, Veitia A, Sank D, Jeffrey E, White T C, Mutus J, Fowler A G, Campbell B, Chen Y, Chen Z, Chiaro B, Dunsworth A, Neill C, O’Malley P, Roushan P, Vainsencher A, Wenner J, Korotkov A N, Cleland A N, Martinis J M 2014 Nature 508 500 Google Scholar
[11]	Buluta I, Nori F 2009 Science 326 108 Google Scholar
[12]	Ashida Y, Gong Z P, Ueda M 2020 Adv. Phys. 69 249 Google Scholar
[13]	Raghu S, Haldane F D M 2008 Phys. Rev. A 78 033834 Google Scholar
[14]	Wang Z, Chong Y, Joannopoulos J D, Soljacic M 2009 Nature 461 772 Google Scholar
[15]	Rechtsman M C, Zeuner J M, Plotnik Y, Lumer Y, Podolsky D, Dreisow F, Nolte S, Segev M, Szameit A 2013 Nature 496 196 Google Scholar
[16]	Hafezi M, Mittal S, Fan J, Migdall A, Taylor J M 2013 Nat. Photonics 7 1001 Google Scholar
[17]	Yan Q, Liu R, Yan Z, Liu B, Chen H, Wang Z, Lu L 2018 Nat. Phys. 14 461 Google Scholar
[18]	Ozawa T, Price H M, Amo A, Goldman N, Hafezi M, Lu L, Rechtsman M C, Schuster D, Simon J, Zilberberg O, Carusotto I 2019 Rev. Mod. Phys. 91 015006 Google Scholar
[19]	Hussein M I, Leamy M J, Ruzzene M 2014 Appl. Mech. Rev. 66 040802 Google Scholar
[20]	Wang P, Lu L, Bertoldi K 2015 Phys. Rev. Lett. 115 104302 Google Scholar
[21]	Xiao Y X, Ma G, Zhang Z Q, Chan C T 2017 Phys. Rev. Lett. 118 166803 Google Scholar
[22]	Li F, Huang X, Lu J, Ma J, Liu Z 2018 Nat. Phys. 14 30 Google Scholar
[23]	Li X X, Li B, Li P B 2020 Phys. Rev. Res. 2 013121 Google Scholar
[24]	Li X X, Li P B, Li H R, Gao H, Li F L 2021 Phys. Rev. Res. 3 013025 Google Scholar
[25]	Kane C L, Lubensky T C 2014 Nat. Phys. 10 39 Google Scholar
[26]	Chen B G g, Upadhyaya N, Vitelli V 2014 Proc. Natl. Acad. Sci. 111 13004 Google Scholar
[27]	Nash L M, Kleckner D, Read A, Vitelli V, Turner A M, Irvine W T M 2015 Proc. Natl. Acad. Sci. 112 14495 Google Scholar
[28]	Chaunsali R, Kim E, Thakkar A, Kevrekidis P G, Yang J 2017 Phys. Rev. Lett. 119 024301 Google Scholar
[29]	Brandenbourger M, Locsin X, Lerner E, Coulais C 2019 Nat. Commun. 10 4608 Google Scholar
[30]	Ghatak A, Brandenbourger M, van Wezel J, Coulais C 2020 Proc. Natl. Acad. Sci. 117 29561 Google Scholar
[31]	罗开发, 余睿 2019 68 220305 Google Scholar Luo K F, Yu R 2019 Acta Phys. Sin. 68 220305 Google Scholar
[32]	刘硕, 张霜, 崔铁军 2021 中国光学 14 736 Google Scholar Liu S, Zhang S, Cui T J 2021 Chinese Optics 14 736 Google Scholar
[33]	Albert V V, Glazman L I, Jiang L 2015 Phys. Rev. Lett. 114 173902 Google Scholar
[34]	Ningyuan J, Owens C, Sommer A, Schuster D, Simon J 2015 Phys. Rev. X 5 021031 Google Scholar
[35]	Lee C H, Imhof S, Berger C, Bayer F, Brehm J, Molenkamp L W, Kiessling T, Thomale R 2018 Commun. Phys. 1 39 Google Scholar
[36]	Imhof S, Berger C, Bayer F, Brehm J, Molenkamp L W, Kiessling T, Schindler F, Lee C H, Greiter M, Neupert T, Thomale R 2018 Nat. Phys. 14 925 Google Scholar
[37]	Ezawa M 2018 Phys. Rev. B 98 201402 Google Scholar
[38]	Helbig T, Hofmann T, Lee C H, Thomale R, Imhof S, Molenkamp L W, Kiessling T 2019 Phys. Rev. B 99 161114 Google Scholar
[39]	Liu S, Gao W, Zhang Q, Ma S, Zhang L, Liu C, Xiang Y J, Cui T J, Zhang S 2019 Research 2019 8609875 Google Scholar
[40]	Bao J, Zou D, Zhang W, He W, Sun H, Zhang X 2019 Phys. Rev. B 100 201406 Google Scholar
[41]	Helbig T, Hofmann T, Imhof S, Abdelghany M, Kiessling T, Molenkamp L W, Lee C H, Szameit A, Greiter M, Thomale R 2020 Nat. Phys. 16 747 Google Scholar
[42]	Lee C H, Sutrisno A, Hofmann T, Helbig T, Liu Y, Ang Y S, Ang L K, Zhang X, Greiter M, Thomale R 2020 Nat. Commun. 11 4385 Google Scholar
[43]	Wu J, Huang X, Lu J, Wu Y, Deng W, Li F, Liu Z 2020 Phys. Rev. B 102 104109 Google Scholar
[44]	Kotwal T, Moseley F, Stegmaier A, Imhof S, Brand H, Kießling T, Thomale R, Ronellenfitsch H, Dunkel J 2021 Proc. Natl. Acad. Sci. 118 e2106411118 Google Scholar
[45]	Dong J, Juričić V, Roy B 2021 Phys. Rev. Res. 3 023056 Google Scholar
[46]	Yang Y, Zhu D, Hang Z, Chong Y 2021 Sci. China: Phys., Mech. Astron. 64 257011 Google Scholar
[47]	Zhang W, Zou D, Pei Q, He W, Bao J, Sun H, Zhang X 2021 Phys. Rev. Lett. 126 146802 Google Scholar
[48]	Wu J, Wang Z, Biao Y, Fei F, Zhang S, Yin Z, Hu Y, Song Z, Wu T, Song F, Yu R 2022 Nat. Electron. 5 635 Google Scholar
[49]	Wang Z, Zeng X T, Biao Y, Yan Z, Yu R 2023 Phys. Rev. Lett. 130 057201 Google Scholar
[50]	Breuer H P, Petruccione F 2002 The Theory of Open Quantum Systems (Oxford: Oxford University Press
[51]	Daley A J 2014 Adv. Phys. 63 77 Google Scholar
[52]	Bender C M, Boettcher S 1998 Phys. Rev. Lett. 80 5243 Google Scholar
[53]	Bender C M 2007 Rep. Prog. Phys. 70 947 Google Scholar
[54]	Longhi S 2019 Opt. Lett. 44 5804 Google Scholar
[55]	Pan J S, Yi W, Gong J 2021 Commun. Phys. 4 261 Google Scholar
[56]	Moca C P, Sticlet D, Dóra B, Zaránd G 2023 Phys. Rev. B 107 115111 Google Scholar
[57]	Lee T E 2016 Phys. Rev. Lett. 116 133903 Google Scholar
[58]	Kunst F K, Edvardsson E, Budich J C, Bergholtz E J 2018 Phys. Rev. Lett. 121 026808 Google Scholar
[59]	Yao S, Wang Z 2018 Phys. Rev. Lett. 121 086803 Google Scholar
[60]	Yao S, Song F, Wang Z 2018 Phys. Rev. Lett. 121 136802 Google Scholar
[61]	Edvardsson E, Kunst F K, Bergholtz E J 2019 Phys. Rev. B 99 081302 Google Scholar
[62]	Ghatak A, Das T 2019 J. Phys.: Condens. Matter 31 263001 Google Scholar
[63]	Song F, Yao S, Wang Z 2019 Phys. Rev. Lett. 123 170401 Google Scholar
[64]	Song F, Yao S, Wang Z 2019 Phys. Rev. Lett. 123 246801 Google Scholar
[65]	Borgnia D S, Kruchkov A J, Slager R J 2020 Phys. Rev. Lett. 124 056802 Google Scholar
[66]	Xiao L, Deng T, Wang K, Zhu G, Wang Z, Yi W, Xue P 2020 Nat. Phys. 16 761 Google Scholar
[67]	Zhang K, Yang Z, Fang C 2020 Phys. Rev. Lett. 125 126402 Google Scholar
[68]	Yang Z, Zhang K, Fang C, Hu J 2020 Phys. Rev. Lett. 125 226402 Google Scholar
[69]	Okuma N, Sato M 2021 Phys. Rev. Lett. 126 176601 Google Scholar
[70]	Liang Q, Xie D, Dong Z, Li H, Li H, Gadway B, Yi W, Yan B 2022 Phys. Rev. Lett. 129 070401 Google Scholar
[71]	Milburn T J, Doppler J, Holmes C A, Portolan S, Rotter S, Rabl P 2015 Phys. Rev. A 92 052124 Google Scholar
[72]	Zhong Q, Christodoulides D N, Khajavikhan M, Makris K G, El-Ganainy R 2018 Phys. Rev. A 97 020105 Google Scholar
[73]	Zhang K L, Wang P, Song Z 2019 Phys. Rev. A 99 042111 Google Scholar
[74]	Liu S, Ma S, Yang C, Zhang L, Gao W, Xiang Y J, Cui T J, Zhang S 2020 Phys. Rev. Appl. 13 014047 Google Scholar
[75]	Heiss W D 2004 J. Phys. A: Math. Gen. 37 2455 Google Scholar
[76]	Moiseyev N 2011 Non-Hermitian Quantum Mechanics (Cambridge: Cambridge University Press
[77]	Okugawa R, Takahashi R, Yokomizo K 2020 Phys. Rev. B 102 241202 Google Scholar
[78]	Zhang X, Tian Y, Jiang J H, Lu M H, Chen Y F 2021 Nat. Commun. 12 5377 Google Scholar
[79]	Zhang X, Zhang T, Lu M H, Chen Y F 2022 Adv. Phys.: X 7 2109431 Google Scholar
[80]	Deng T S, Yi W 2019 Phys. Rev. B 100 035102 Google Scholar
[81]	Yokomizo K, Murakami S 2019 Phys. Rev. Lett. 123 066404 Google Scholar
[82]	Zhu X, Wang H, Gupta S K, Zhang H, Xie B, Lu M, Chen Y 2020 Phys. Rev. Res. 2 013280 Google Scholar
[83]	Yokomizo K, Murakami S 2020 Prog. Theor. Exp. Phys. 2020 12A102 Google Scholar
[84]	Xiao L, Deng T, Wang K, Wang Z, Yi W, Xue P 2021 Phys. Rev. Lett. 126 230402 Google Scholar
[85]	Wang K, Li T, Xiao L, Han Y, Yi W, Xue P 2021 Phys. Rev. Lett. 127 270602 Google Scholar
[86]	Yokomizo K 2022 Non-Bloch Band Theory of Non Hermitian Systems (Singapore: Springer Nature
[87]	Yokomizo K, Murakami S 2023 Phys. Rev. B 107 195112 Google Scholar
[88]	Shi K, Tian M, Sun F X, Zhang W 2023 Phys. Rev. B 107 205154 Google Scholar
[89]	Zhou H, Lee J Y 2019 Phys. Rev. B 99 235112 Google Scholar
[90]	Kawabata K, Shiozaki K, Ueda M, Sato M 2019 Phys. Rev. X 9 041015 Google Scholar
[91]	Kawabata K, Okuma N, Sato M 2020 Phys. Rev. B 101 195147 Google Scholar
[92]	Bergholtz E J, Budich J C, Kunst F K 2021 Rev. Mod. Phys. 93 015005 Google Scholar
[93]	Liu C H, Zhang K, Yang Z, Chen S 2020 Phys. Rev. Res. 2 043167 Google Scholar
[94]	He P, Liu Y G, Wang J T, Zhu S L 2022 Phys. Rev. A 105 023311 Google Scholar
[95]	Niu X, Li J, Wu S L, Yi X X 2023 Phys. Rev. A 108 032214 Google Scholar
[96]	Nakanishi Y, Sasamoto T 2022 Phys. Rev. A 105 022219 Google Scholar
[97]	Li T, Zhang Y S, Yi W 2022 Phys. Rev. B 105 125111 Google Scholar
[98]	Purkayastha A 2022 Phys. Rev. A 105 062204 Google Scholar
[99]	Roccati F, Palma G M, Ciccarello F, Bagarello F 2022 Open Syst. Inf. Dyn. 29 2250004 Google Scholar
[100]	Niu X, Wang J 2023 arXiv: 2211.04233 [quant-ph
[101]	Liu Y G, Chen S 2023 Phys. Rev. B 107 134307 Google Scholar
[102]	Strang G 2023 Introduction to Linear Algebra (6th Ed.) (Wellesley-Cambridge Press
[103]	Demange G, Graefe E M 2011 J. Phys. A: Math. Theor. 45 025303 Google Scholar
[104]	Rotter I 2009 J. Phys. A: Math. Theor 42 153001 Google Scholar
[105]	Mostafazadeh A 2002 J. Math. Phys. 43 205 Google Scholar
[106]	Mostafazadeh A 2002 J. Math. Phys. 43 3944 Google Scholar
[107]	Xiong Y 2018 J. Phys. Commun. 2 035043 Google Scholar
[108]	Ryu S, Schnyder A P, Furusaki A, Ludwig A W W 2010 New J. Phys 12 065010 Google Scholar
[109]	Xu Z C, Zhou Z, Cheng E, Lang L J, Zhu S L 2022 Sci. China: Phys., Mech. Astron. 65 283011 Google Scholar
[110]	Chen W, Kaya Özdemir Ş, Zhao G, Wiersig J, Yang L 2017 Nature 548 192 Google Scholar
[111]	Wiersig J 2014 Phys. Rev. Lett. 112 203901 Google Scholar
[112]	Kato T 1995 Perturbation Theory for Linear Operators (Berlin, Heidelberg: Springer
[113]	Schindler J, Li A, Zheng M C, Ellis F M, Kottos T 2011 Phys. Rev. A 84 040101 Google Scholar
[114]	Dong Z, Li Z, Yang F, Qiu C W, Ho J S 2019 Nat. Electron. 2 335 Google Scholar
[115]	Zhou B B, Wang L F, Dong L, Huang Q A 2021 J. Phys. Commun. 5 045010 Google Scholar
[116]	Zeng C, Zhu K, Sun Y, Li G, Guo Z, Jiang J, Li Y, Jiang H, Yang Y, Chen H 2021 New J. Phys 23 063008 Google Scholar
[117]	成恩宏, 郎利君 2022 71 160301 Google Scholar Cheng E H, Lang L J 2022 Acta Phys. Sin. 71 160301 Google Scholar
[118]	Hofmann T, Helbig T, Schindler F, Salgo N, Brzezińska M, Greiter M, Kiessling T, Wolf D, Vollhardt A, Kabaši A, Lee C H, Bilušić A, Thomale R, Neupert T 2020 Phys. Rev. Res. 2 023265 Google Scholar
[119]	Liu S, Shao R, Ma S, Zhang L, You O, Wu H, Xiang Y J, Cui T J, Zhang S 2021 Research 2 5608038 Google Scholar
[120]	Stegmaier A, Imhof S, Helbig T, Hofmann T, Lee C H, Kremer M, Fritzsche A, Feichtner T, Klembt S, Höfling S, Boettcher I, Fulga I C, Ma L, Schmidt O G, Greiter M, Kiessling T, Szameit A, Thomale R 2021 Phys. Rev. Lett. 126 215302 Google Scholar
[121]	Zou D, Chen T, He W, Bao J, Lee C H, Sun H, Zhang X 2021 Nat. Commun. 12 7201 Google Scholar
[122]	Wu J, Huang X, Yang Y, Deng W, Lu J, Deng W, Liu Z 2022 Phys. Rev. B 105 195127 Google Scholar
[123]	Zhang W, Di F, Yuan H, Wang H, Zheng X, He L, Sun H, Zhang X 2022 Phys. Rev. B 105 195131 Google Scholar
[124]	Shang C, Liu S, Shao R, Han P, Zang X, Zhang X, Salama K N, Gao W, Lee C H, Thomale R, Manchon A, Zhang S, Cui T J, Schwingenschlögl U 2022 Adv. Sci. 9 2202922 Google Scholar
[125]	Zhang X, Zhang B, Zhao W, Lee C H 2022 arXiv: 2211.09152 [cond-mat.mes-hall
[126]	Zhu P, Sun X Q, Hughes T L, Bahl G 2023 Nat. Commun. 14 720 Google Scholar
[127]	Wu M, Zhao Q, Kang L, Weng M, Chi Z, Peng R, Liu J, Werner D H, Meng Y, Zhou J 2023 Phys. Rev. B 107 064307 Google Scholar
[128]	Kim Y, Park H C, Kyung M, Lee K, Ryu J W, You O, Zhang S, Min B, Park M J 2023 arXiv: 2303.13721 [cond-mat.mes-hall
[129]	Su L, Guo C X, Wang Y, Li L, Ruan X, Du Y, Chen S, Zheng D 2023 Chin. Phys. B 32 038401 Google Scholar
[130]	Yin K, Hao X, Huang Y, Zou J, Ma X, Dong T 2023 Phys. Rev. Applied 20 L021003 Google Scholar
[131]	Ezawa M 2019 Phys. Rev. B 99 121411 Google Scholar
[132]	Zhou B B, Deng W J, Wang L F, Dong L, Huang Q A 2020 Phys. Rev. Appl. 13 064022 Google Scholar
[133]	Schindler J, Lin Z, Lee J M, Ramezani H, Ellis F M, Kottos T 2012 J. Phys. A: Math. Theor. 45 444029 Google Scholar
[134]	Ramezani H, Schindler J, Ellis F M, Günther U, Kottos T 2012 Phys. Rev. A 85 062122 Google Scholar
[135]	Wang T, Fang J, Xie Z, Dong N, Joglekar Y N, Wang Z, Li J, Luo L 2020 Eur. Phys. J. D 74 167 Google Scholar
[136]	Chen W K 2002 The Circuits and Filters Handbook (CRC Press
[137]	Hofmann T, Helbig T, Lee C H, Greiter M, Thomale R 2019 Phys. Rev. Lett. 122 247702 Google Scholar
[138]	Zhang H, Chen T, Li L, Lee C H, Zhang X 2023 Phys. Rev. B 107 085426 Google Scholar
[139]	Yuan H, Zhang W, Zhou Z, Wang W, Pan N, Feng Y, Sun H, Zhang X 2023 Adv. Sci. 2301128 Google Scholar
[140]	Chen P Y, Sakhdari M, Hajizadegan M, Cui Q, Cheng M M C, El-Ganainy R, Alù A 2018 Nat. Electron. 1 297 Google Scholar
[141]	Sakhdari M, Hajizadegan M, Zhong Q, Christodoulides D N, El-Ganainy R, Chen P Y 2019 Phys. Rev. Lett. 123 193901 Google Scholar
[142]	Yin K, Huang Y, Ma C, Hao X, Gao X, Ma X, Dong T 2022 Appl. Phys. Lett. 120 194101 Google Scholar
[143]	Wu F Y 2004 J. Phys. A: Math. Gen. 37 6653 Google Scholar
[144]	Li Z, Wu J, Huang X, Lu J, Li F, Deng W, Liu Z 2020 Appl. Phys. Lett. 116 263501 Google Scholar
[145]	Deng W, Chen T, Zhang X 2022 Phys. Rev. Res. 4 033109 Google Scholar
[146]	Tang C, Yang H, Song L, Yao X, Yan P, Cao Y 2023 Phys. Rev. B 108 035410 Google Scholar
[147]	Lang L J, Weng Y, Zhang Y, Cheng E, Liang Q 2021 Phys. Rev. B 103 014302 Google Scholar
[148]	Chitsazi M, Li H, Ellis F M, Kottos T 2017 Phys. Rev. Lett. 119 093901 Google Scholar
[149]	Su L, Jiang H, Wang Z, Chen S, Zheng D 2023 Phys. Rev. B 107 184108 Google Scholar
[150]	Lee C H, Li L, Gong J 2019 Phys. Rev. Lett. 123 016805 Google Scholar
[151]	Li L, Lee C H, Gong J 2020 Phys. Rev. Lett. 124 250402 Google Scholar
[152]	Yin K, Huang Y, Yin W, Hao X, Ma X, Dong T 2022 Phys. Rev. Appl. 18 064020 Google Scholar
[153]	Zhang M, Sweeney W, Hsu C W, Yang L, Stone A D, Jiang L 2019 Phys. Rev. Lett. 123 180501 Google Scholar
[154]	Kononchuk R, Cai J, Ellis F, Thevamaran R, Kottos T 2022 Nature 607 697 Google Scholar
[155]	Langbein W 2018 Phys. Rev. A 98 023805 Google Scholar

施引文献

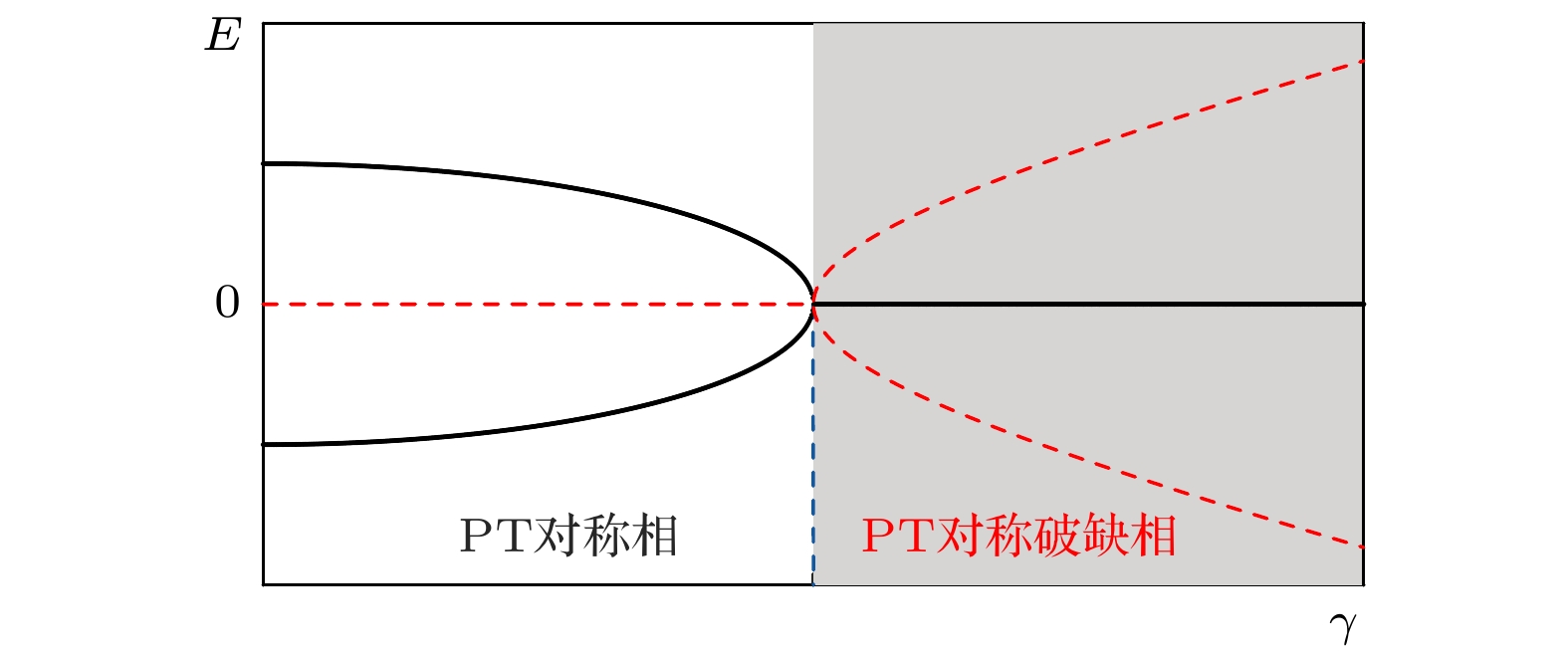
图 1 能量E的实部(实线)和虚部(虚线)随非厄米强度γ的变化. 点线处为PT转变点, 其左侧为PT对称相(白色区域), 右侧为PT对称破缺相(灰色区域)

Fig. 1. The real (solid lines) and imaginary (dashed lines) parts of the energy E versus the strength γ of the non-Hermiticity. The dotted line indicates the PT transition point, to the left side of which is the PT symmetric phase (white region) and to the right side of which is the PT-broken phase (gray region).

下载: 全尺寸图片幻灯片

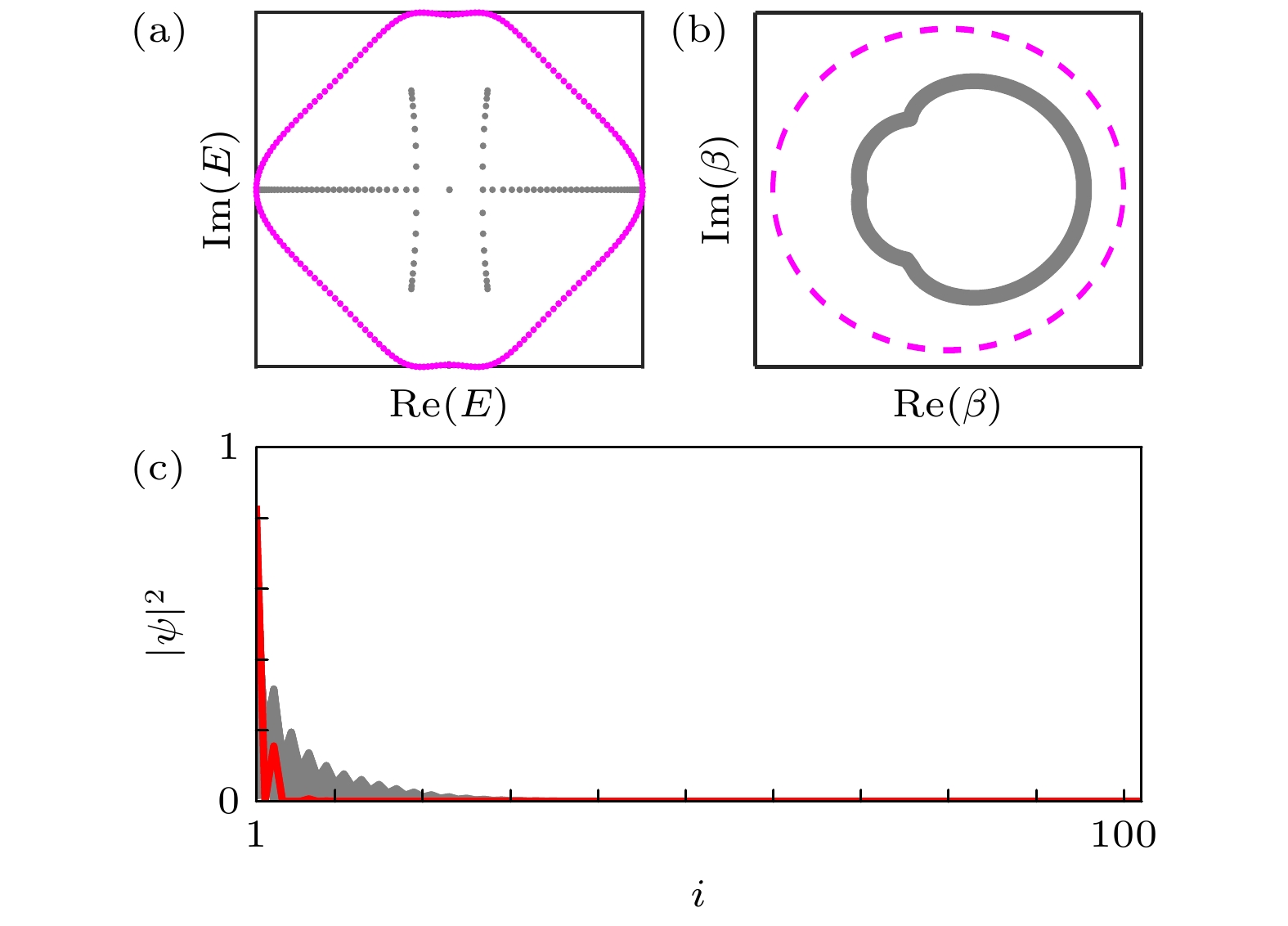
图 2 (a)非厄米SSH模型^[59]分别在开边界(粉色)和周期边界(灰色)条件下的能谱E在复平面的示意图; (b)与(a)中能谱相对应的布里渊区(灰色)和广义布里渊区(粉色)的示意图, 其中β的定义见正文; (c)开边界条件下拓扑边缘态(红色)和趋肤态(灰色)的在实空间的几率分布$|\psi_i|^2$示意图, i为格点标记

Fig. 2. (a) The sketch of the energy spectra in complex plane for the non-Hermitian SSH model in Ref. 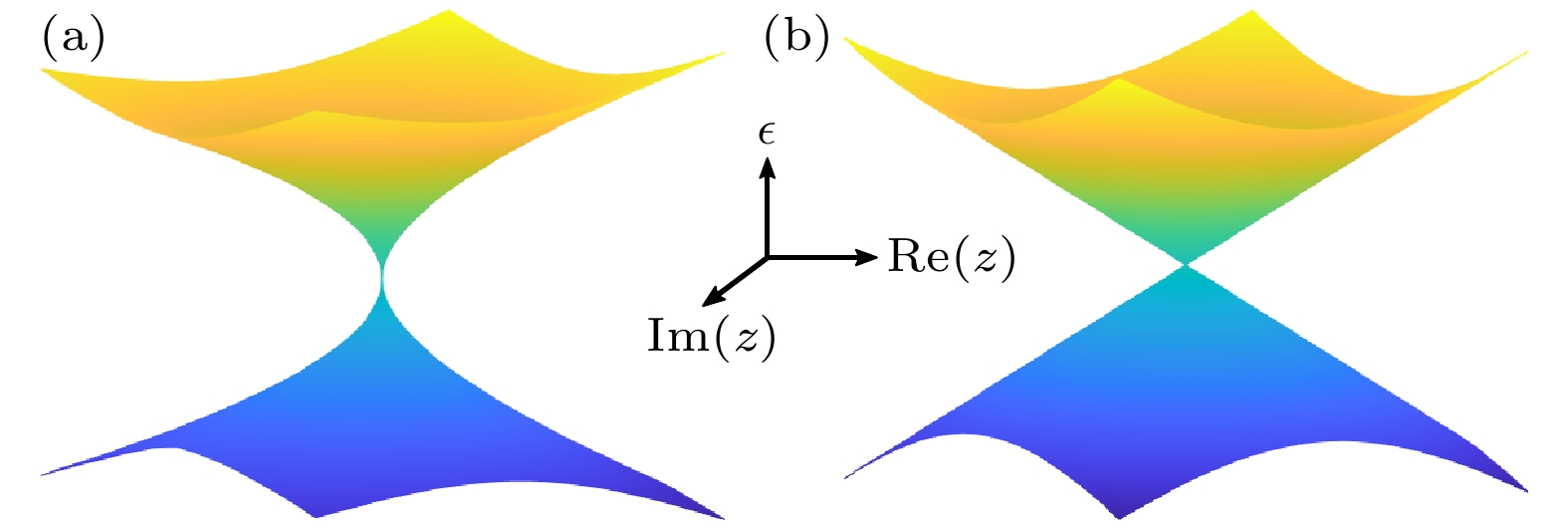[59] respectively under open (pink) and periodic (gray) boundary conditions; (b) the sketch of the Brillouin zone (black) and the generalized Brillouin zone (pink) corresponding to the spectra with the same colors in (a), where the definition of β can be referred to in the main text; (c) the sketch of probability distribution $|\psi_i|^2$ of the topological end state (red) and the skin bulk states (gray) in real space under open boundary conditions, where i is the site index.

下载: 全尺寸图片幻灯片

图 3 (a)能谱ε随微扰z在二阶EP附近劈裂的示意图, 具有$\varepsilon \propto z^{1/2}$的形式^[110]; (b)能谱ε随微扰z在传统的二重简并点附近劈裂的示意图, 具有$\varepsilon \propto z$的形式^[110]

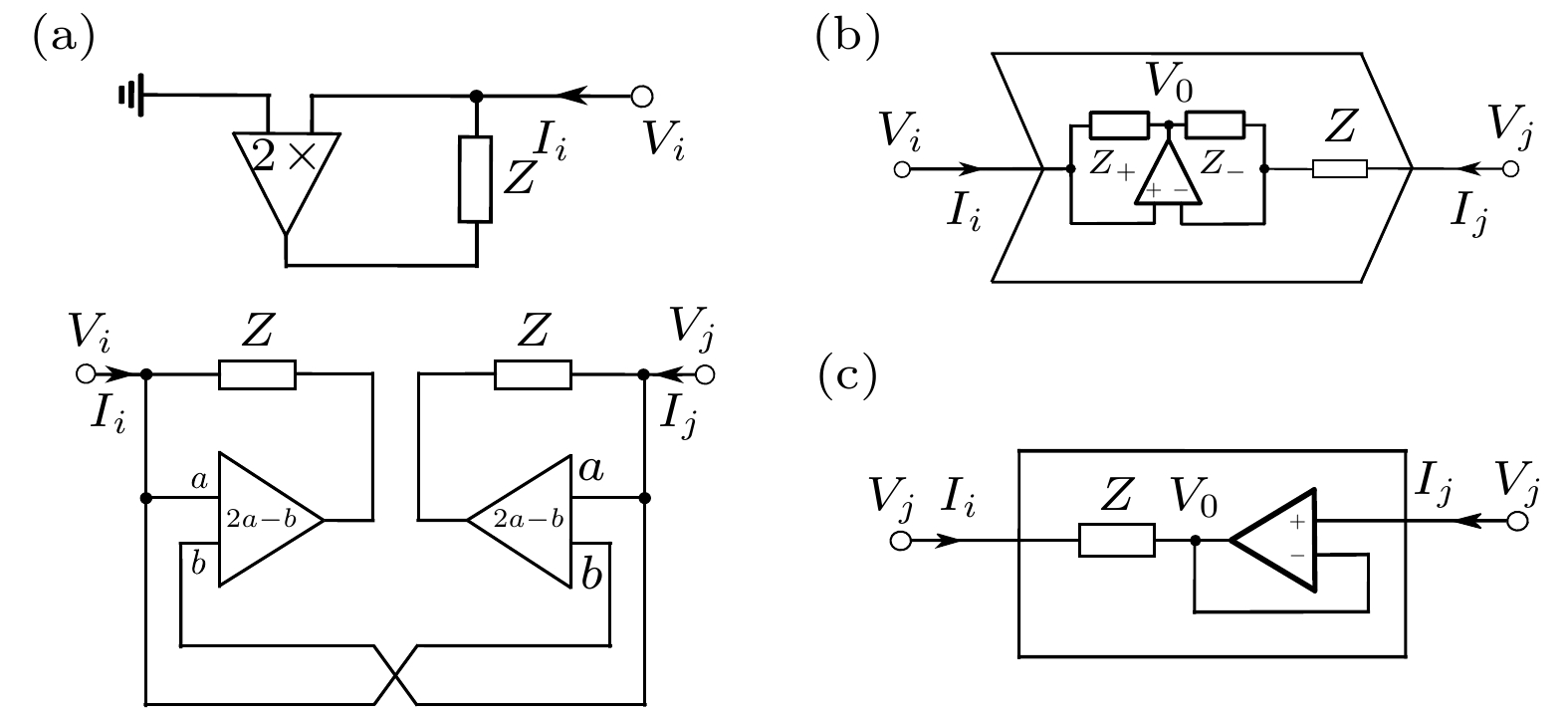
Fig. 3. (a) The sketch of energy spectra ε versus the perturbation z around a two-order EP, satisfying $\varepsilon \propto z^{1/2}$ ^[110]; (b) the sketch of energy spectra ε versus the perturbation z around a traditional two-fold degenerate point, satisfying $\varepsilon \propto z$^[110].

下载: 全尺寸图片幻灯片

图 4 二聚体电路示意图^[132]. 由电感耦合的两个RLC回路构成, 其中M为互感, $-R$代表负电阻

Fig. 4. The sketch of the dimer circuit consisting of two inductively coupled RLC tanks^[132], where M is the mutual inductance and $-R$ represents an negative resistance.

下载: 全尺寸图片幻灯片

图 5 (a)负阻抗的电路原理图^[133], 上下图分别表示对地端口和自由双端口的情况; (b) INIC的电路原理图^[137]; (c)电压跟随器的电路原理图^[136]. 以上所用运放的等效增益函数可用加法器和乘法器实现

Fig. 5. (a) The schematic circuit for negative impedance^[133], where the upper and lower panels represent the one-port and two-port cases, respectively; (b) the schematic circuit for INIC^[136]; (c) the schematic circuit for a voltage follower^[136]. The equivalent gain functions of the operational amplifiers used above can be implemented using adders and multipliers.

下载: 全尺寸图片幻灯片

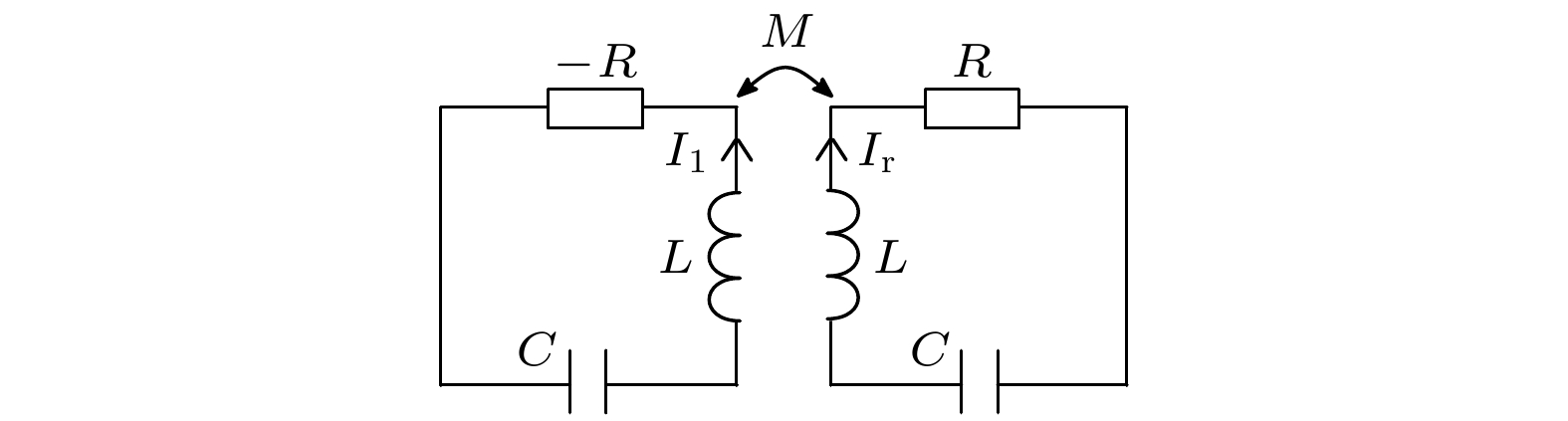
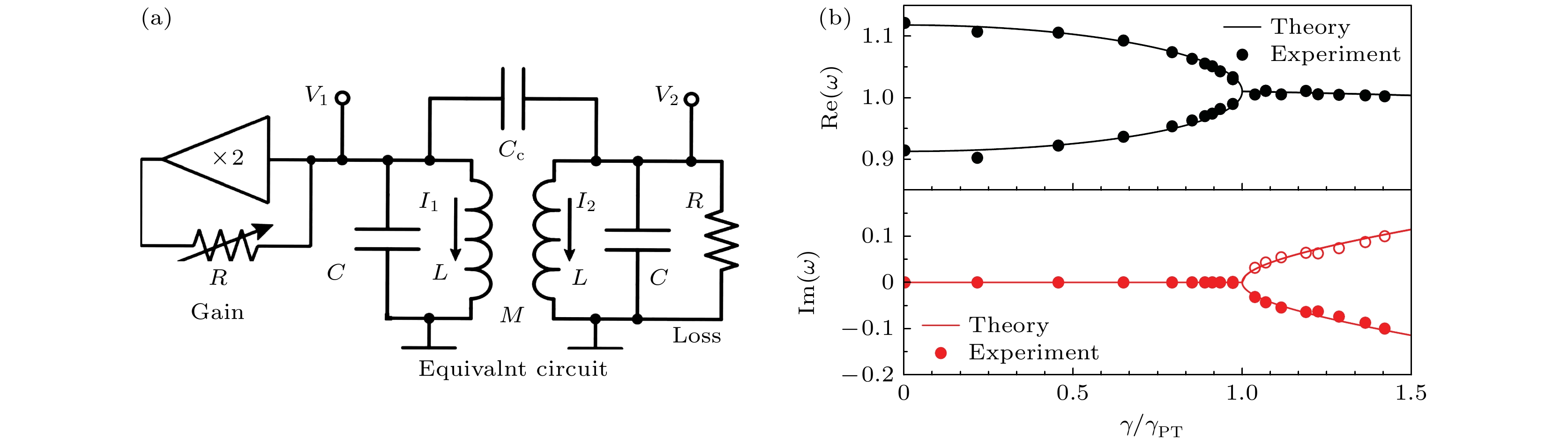
图 6 (a) PT对称的二聚体电路, 电路中的增益和损耗部分通过电容或互感耦合; (b) 实验测量的本征频率随着增益/损耗参数$\gamma/\gamma_{\rm{PT}}$的变换, 在$\gamma/\gamma_{\rm{PT}}=1$时发生PT对称破缺. 图来源于文献[113], 版权属于美国物理学会

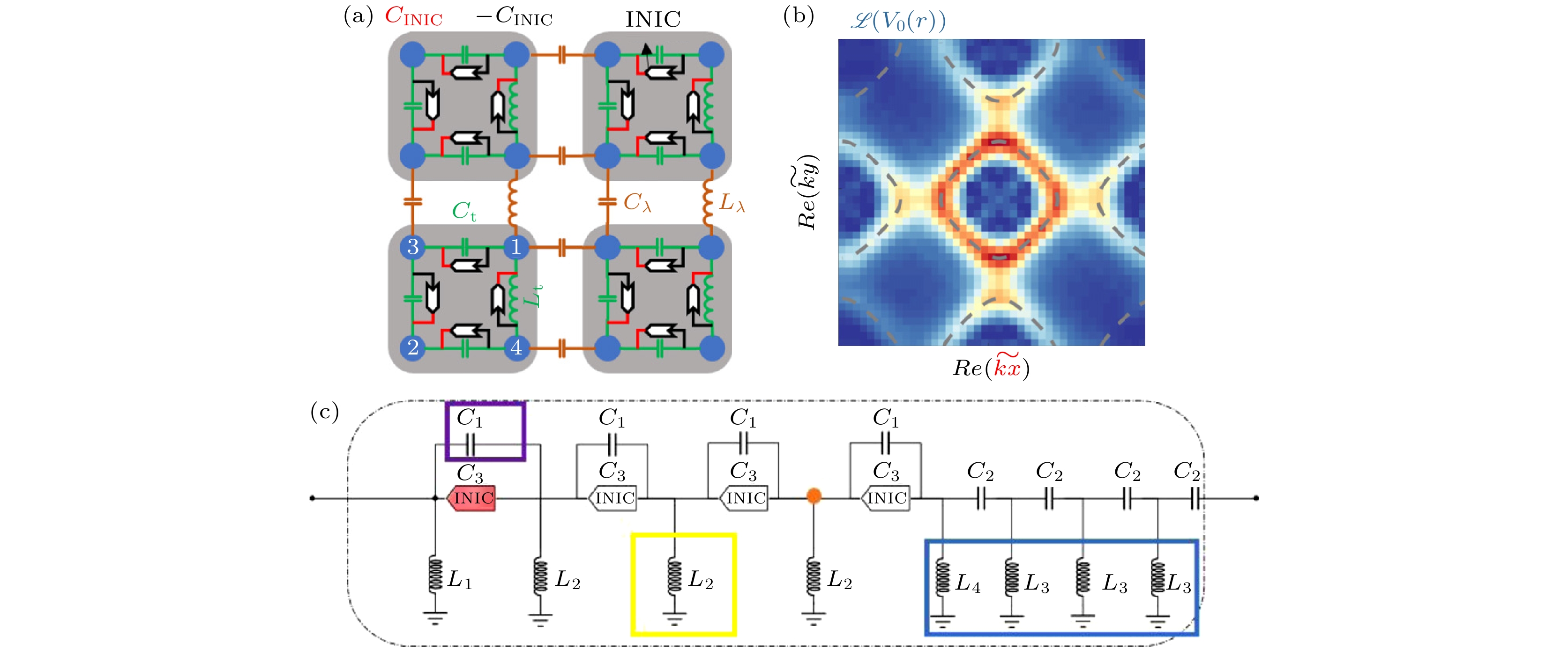
Fig. 6. (a) Circuit diagram of a PT-symmetric dimer, where the gain and loss parts are capacitively or inductively coupled; (b) experimentally measured eigenfrequencies versus the gain/loss parameter $\gamma/\gamma_{\rm{PT}}$, where the PT symmetry breaking occurs at $\gamma/\gamma_{\rm{PT}}=1$. All figures are adapted from Ref.[113] with the copyright © 2011 by the American Physical Society.

下载: 全尺寸图片幻灯片

图 7 (a)非布洛赫演化的拓扑电路; (b)实验测得的电压分布经拉普拉斯变换后在广义布里渊区中的等频分布; (c)四次方根非厄米SSH模型的电路图. 图(a)和(b)来源于文献[127], 图(c)来源于文献[145]. 版权属于美国物理学会

Fig. 7. (a) Topolectrical circuit for the non-Bloch dynamics; (b) the isofrequency contour of the measured voltage distribution through the Laplace transform in the GBZ; (c) circuit diagram of a 4th-root non-Hermitian SSH model. Subfigures (a) and (b) are adapted from Ref. [127], and Figure (c) from Ref. [145]. Copyright © 2023 and 2022 by the American Physical Society.

下载: 全尺寸图片幻灯片

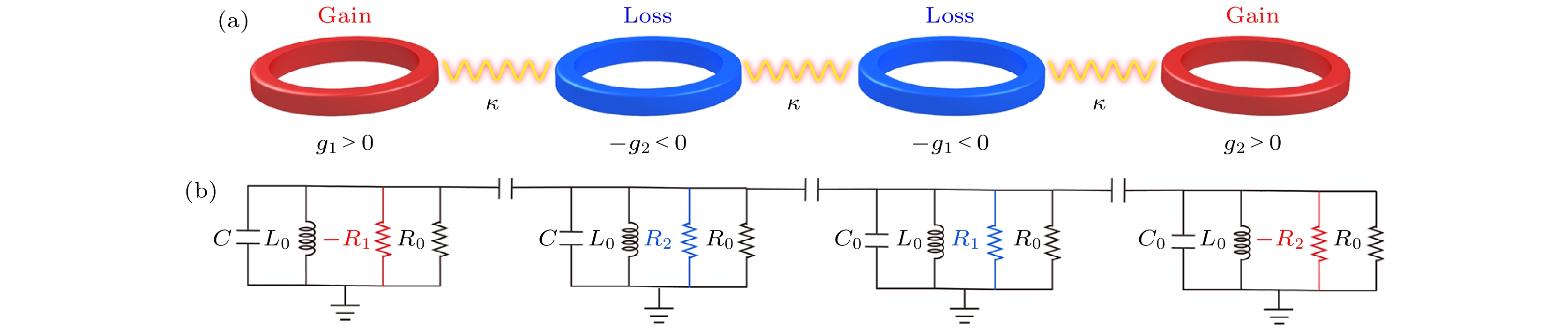
图 8 (a)单纯由增益/损耗诱导的非厄米拓扑模型; (b)实现(a)中模型的电路图. 图均来源于文献[74], 版权属于美国物理学会

Fig. 8. (a) A non-Hermitian topological model whose topology is purely induced by gain/loss; (b) circuit diagram for the realization of the model in (a). All figures are adapted from Ref.[74] with the copyright © 2020 by the American Physical Society.

下载: 全尺寸图片幻灯片

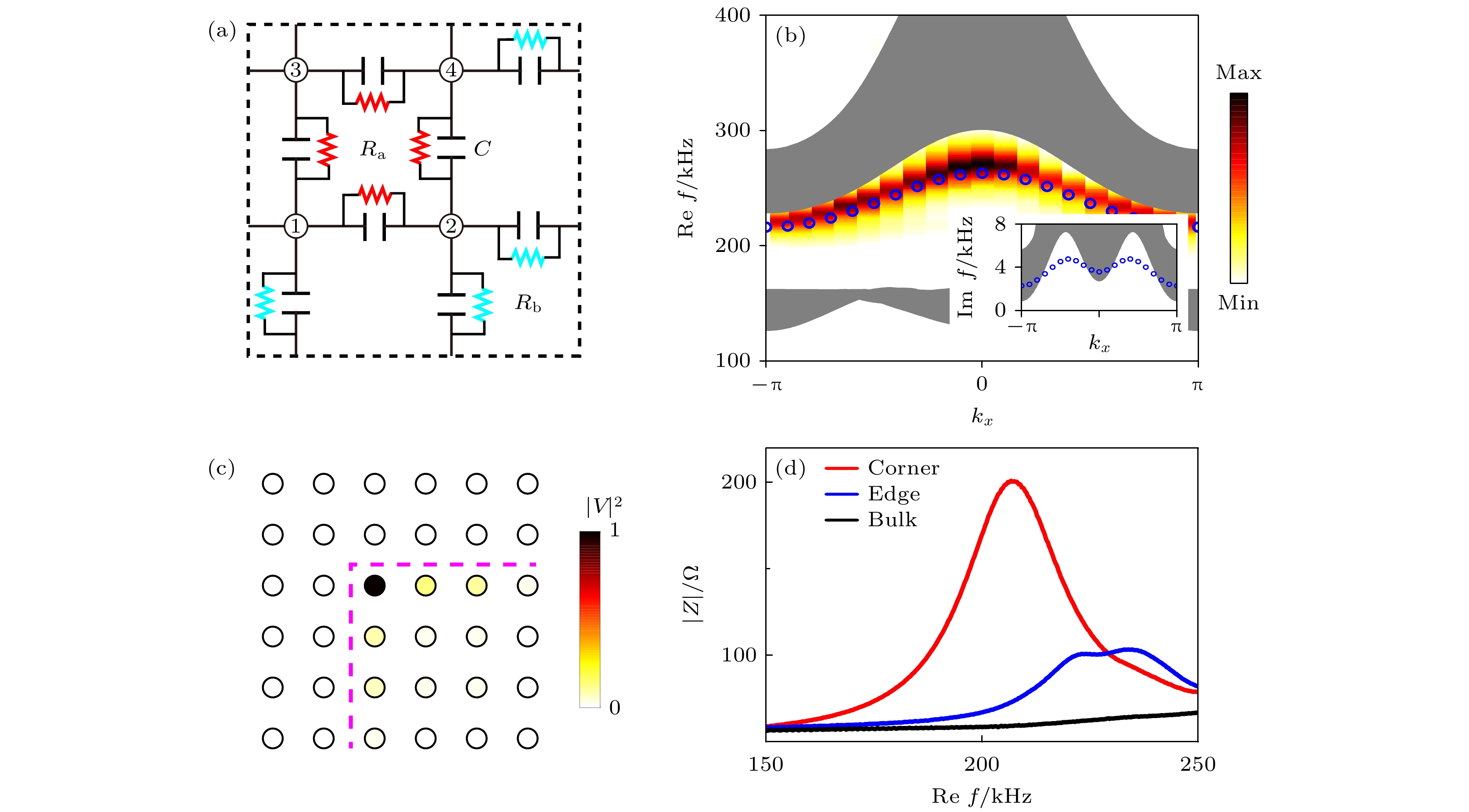
图 9 (a)非厄米二阶拓扑电路的原胞示意图; (b)能隙间的一维边缘态, 彩色和圆圈分别表示实验测量和理论计算的结果; (c)实验测量的零维角态的电压分布; (d)实验测量的角态、边缘态和体态的阻抗响应随驱动频率的变化. 图均来源于文献[122], 版权属于美国物理学会

Fig. 9. (a) Circuit diagram of a unit cell of the non-Hermitian second-order topological electric circuit; (b) one-dimensional gapped edge states, where the color map and the blue circles represent the data from the experiment and the theoretical calculation, respectively; (c) experimental voltage distributions of the zeroth dimensional corner states; (d) experimental impedance responses of corner states, edge states, and bulk states to the driving frequency. All figures are adapted from Ref. [122] with the copyright © 2022 by the American Physical Society.

下载: 全尺寸图片幻灯片

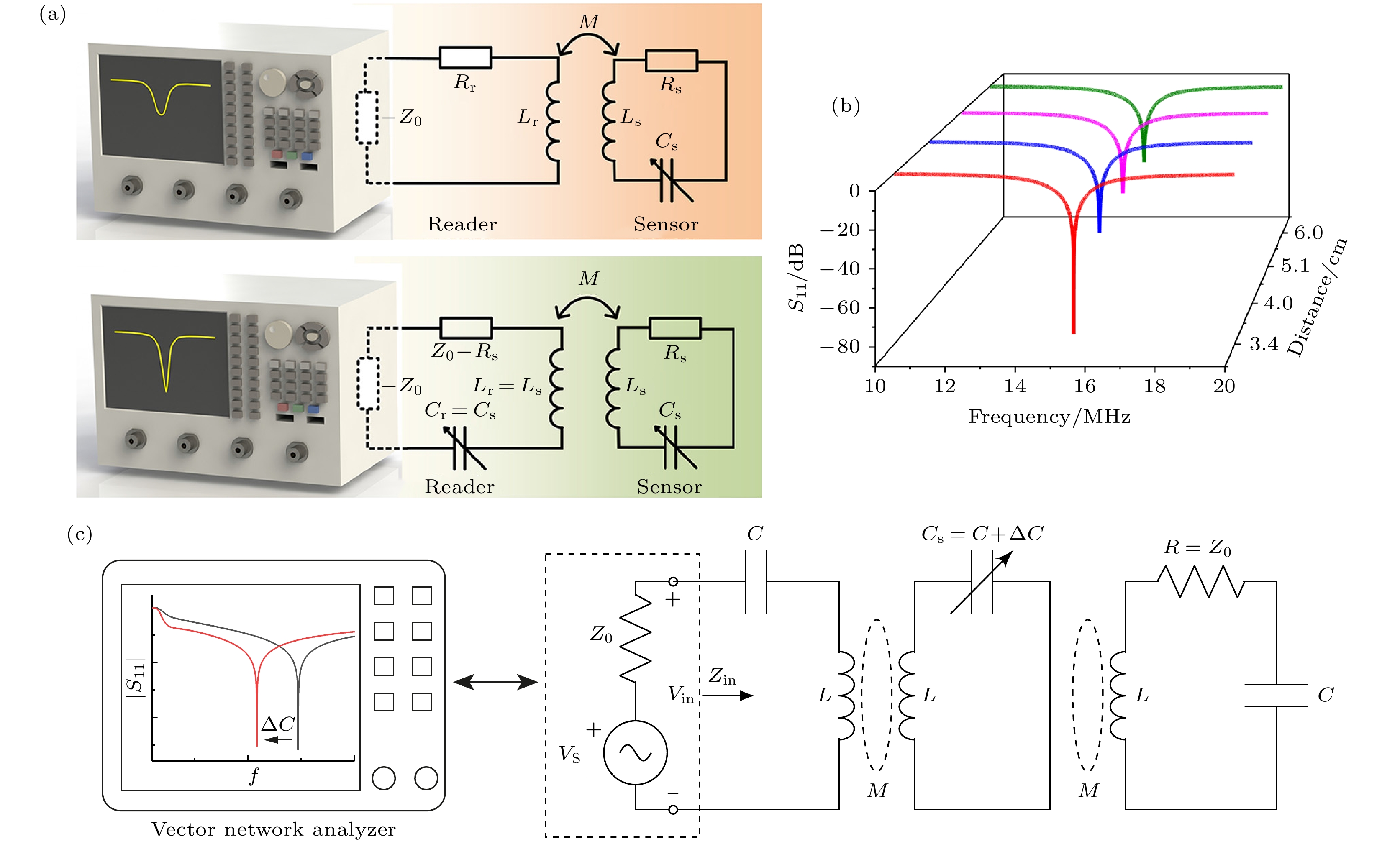
图 10 (a)传统的被动无线传感器与基于PT对称性的被动无线传感器的电路图; (b)基于PT对称性的被动无线传感器的反射谱的测量结果; (c)具有PT对称性的三阶无线传感器的电路图. 图(a)和(b)来源于文献[132], 图(c)来源于文献[152], 版权属于美国物理学会

Fig. 10. (a) Circuit diagrams of a conventional passive wireless sensor and a PT-symmetry-based passive wireless sensor; (b) measured reflection spectra for the PT-symmetry-based passive wireless sensor; (c) circuit diagram of a PT symmetric third-order wireless sensing system. Subfigures (a) and (b) are adapted from Ref. [132] and subfigure (c) from Ref. [152], with copyright © 2020 and 2022 by the American Physical Society.

下载: 全尺寸图片幻灯片

map

[1]	Feynman R P 1982 Int. J. Theor. Phys. 21 467 Google Scholar
[2]	Greiner M, Mandel O, Esslinger T, Hänsch T W, Bloch I 2002 Nature 415 39 Google Scholar
[3]	Billy J, Josse V, Zuo Z, Bernard A, Hambrecht B, Lugan P, Clement D, Sanchez-Palencia L, Bouyer P, Aspect A 2008 Nature 453 891 Google Scholar
[4]	Zhang D W, Zhu Y Q, Zhao Y X, Yan H, Zhu S L 2018 Adv. Phys. 67 253 Google Scholar
[5]	Friedenauer A, Schmitz H, Glueckert J T, Porras D, Schaetz T 2008 Nat. Phys. 4 757 Google Scholar
[6]	Barreiro J T, Müller M, Schindler P, Nigg D, Monz T, Chwalla M, Hennrich M, Roos C F, Zoller P, Blatt R 2011 Nature 470 486 Google Scholar
[7]	Blatt R, Roos C F 2012 Nat. Phys. 8 277 Google Scholar
[8]	You J Q, Shi X F, Hu X, Nori F 2010 Phys. Rev. B 81 014505 Google Scholar
[9]	Georgescu I, Ashhab S, Nori F 2014 Rev. Mod. Phys. 86 153 Google Scholar
[10]	Barends R, Kelly J, Megrant A, Veitia A, Sank D, Jeffrey E, White T C, Mutus J, Fowler A G, Campbell B, Chen Y, Chen Z, Chiaro B, Dunsworth A, Neill C, O’Malley P, Roushan P, Vainsencher A, Wenner J, Korotkov A N, Cleland A N, Martinis J M 2014 Nature 508 500 Google Scholar
[11]	Buluta I, Nori F 2009 Science 326 108 Google Scholar
[12]	Ashida Y, Gong Z P, Ueda M 2020 Adv. Phys. 69 249 Google Scholar
[13]	Raghu S, Haldane F D M 2008 Phys. Rev. A 78 033834 Google Scholar
[14]	Wang Z, Chong Y, Joannopoulos J D, Soljacic M 2009 Nature 461 772 Google Scholar
[15]	Rechtsman M C, Zeuner J M, Plotnik Y, Lumer Y, Podolsky D, Dreisow F, Nolte S, Segev M, Szameit A 2013 Nature 496 196 Google Scholar
[16]	Hafezi M, Mittal S, Fan J, Migdall A, Taylor J M 2013 Nat. Photonics 7 1001 Google Scholar
[17]	Yan Q, Liu R, Yan Z, Liu B, Chen H, Wang Z, Lu L 2018 Nat. Phys. 14 461 Google Scholar
[18]	Ozawa T, Price H M, Amo A, Goldman N, Hafezi M, Lu L, Rechtsman M C, Schuster D, Simon J, Zilberberg O, Carusotto I 2019 Rev. Mod. Phys. 91 015006 Google Scholar
[19]	Hussein M I, Leamy M J, Ruzzene M 2014 Appl. Mech. Rev. 66 040802 Google Scholar
[20]	Wang P, Lu L, Bertoldi K 2015 Phys. Rev. Lett. 115 104302 Google Scholar
[21]	Xiao Y X, Ma G, Zhang Z Q, Chan C T 2017 Phys. Rev. Lett. 118 166803 Google Scholar
[22]	Li F, Huang X, Lu J, Ma J, Liu Z 2018 Nat. Phys. 14 30 Google Scholar
[23]	Li X X, Li B, Li P B 2020 Phys. Rev. Res. 2 013121 Google Scholar
[24]	Li X X, Li P B, Li H R, Gao H, Li F L 2021 Phys. Rev. Res. 3 013025 Google Scholar
[25]	Kane C L, Lubensky T C 2014 Nat. Phys. 10 39 Google Scholar
[26]	Chen B G g, Upadhyaya N, Vitelli V 2014 Proc. Natl. Acad. Sci. 111 13004 Google Scholar
[27]	Nash L M, Kleckner D, Read A, Vitelli V, Turner A M, Irvine W T M 2015 Proc. Natl. Acad. Sci. 112 14495 Google Scholar
[28]	Chaunsali R, Kim E, Thakkar A, Kevrekidis P G, Yang J 2017 Phys. Rev. Lett. 119 024301 Google Scholar
[29]	Brandenbourger M, Locsin X, Lerner E, Coulais C 2019 Nat. Commun. 10 4608 Google Scholar
[30]	Ghatak A, Brandenbourger M, van Wezel J, Coulais C 2020 Proc. Natl. Acad. Sci. 117 29561 Google Scholar
[31]	罗开发, 余睿 2019 68 220305 Google Scholar Luo K F, Yu R 2019 Acta Phys. Sin. 68 220305 Google Scholar
[32]	刘硕, 张霜, 崔铁军 2021 中国光学 14 736 Google Scholar Liu S, Zhang S, Cui T J 2021 Chinese Optics 14 736 Google Scholar
[33]	Albert V V, Glazman L I, Jiang L 2015 Phys. Rev. Lett. 114 173902 Google Scholar
[34]	Ningyuan J, Owens C, Sommer A, Schuster D, Simon J 2015 Phys. Rev. X 5 021031 Google Scholar
[35]	Lee C H, Imhof S, Berger C, Bayer F, Brehm J, Molenkamp L W, Kiessling T, Thomale R 2018 Commun. Phys. 1 39 Google Scholar
[36]	Imhof S, Berger C, Bayer F, Brehm J, Molenkamp L W, Kiessling T, Schindler F, Lee C H, Greiter M, Neupert T, Thomale R 2018 Nat. Phys. 14 925 Google Scholar
[37]	Ezawa M 2018 Phys. Rev. B 98 201402 Google Scholar
[38]	Helbig T, Hofmann T, Lee C H, Thomale R, Imhof S, Molenkamp L W, Kiessling T 2019 Phys. Rev. B 99 161114 Google Scholar
[39]	Liu S, Gao W, Zhang Q, Ma S, Zhang L, Liu C, Xiang Y J, Cui T J, Zhang S 2019 Research 2019 8609875 Google Scholar
[40]	Bao J, Zou D, Zhang W, He W, Sun H, Zhang X 2019 Phys. Rev. B 100 201406 Google Scholar
[41]	Helbig T, Hofmann T, Imhof S, Abdelghany M, Kiessling T, Molenkamp L W, Lee C H, Szameit A, Greiter M, Thomale R 2020 Nat. Phys. 16 747 Google Scholar
[42]	Lee C H, Sutrisno A, Hofmann T, Helbig T, Liu Y, Ang Y S, Ang L K, Zhang X, Greiter M, Thomale R 2020 Nat. Commun. 11 4385 Google Scholar
[43]	Wu J, Huang X, Lu J, Wu Y, Deng W, Li F, Liu Z 2020 Phys. Rev. B 102 104109 Google Scholar
[44]	Kotwal T, Moseley F, Stegmaier A, Imhof S, Brand H, Kießling T, Thomale R, Ronellenfitsch H, Dunkel J 2021 Proc. Natl. Acad. Sci. 118 e2106411118 Google Scholar
[45]	Dong J, Juričić V, Roy B 2021 Phys. Rev. Res. 3 023056 Google Scholar
[46]	Yang Y, Zhu D, Hang Z, Chong Y 2021 Sci. China: Phys., Mech. Astron. 64 257011 Google Scholar
[47]	Zhang W, Zou D, Pei Q, He W, Bao J, Sun H, Zhang X 2021 Phys. Rev. Lett. 126 146802 Google Scholar
[48]	Wu J, Wang Z, Biao Y, Fei F, Zhang S, Yin Z, Hu Y, Song Z, Wu T, Song F, Yu R 2022 Nat. Electron. 5 635 Google Scholar
[49]	Wang Z, Zeng X T, Biao Y, Yan Z, Yu R 2023 Phys. Rev. Lett. 130 057201 Google Scholar
[50]	Breuer H P, Petruccione F 2002 The Theory of Open Quantum Systems (Oxford: Oxford University Press
[51]	Daley A J 2014 Adv. Phys. 63 77 Google Scholar
[52]	Bender C M, Boettcher S 1998 Phys. Rev. Lett. 80 5243 Google Scholar
[53]	Bender C M 2007 Rep. Prog. Phys. 70 947 Google Scholar
[54]	Longhi S 2019 Opt. Lett. 44 5804 Google Scholar
[55]	Pan J S, Yi W, Gong J 2021 Commun. Phys. 4 261 Google Scholar
[56]	Moca C P, Sticlet D, Dóra B, Zaránd G 2023 Phys. Rev. B 107 115111 Google Scholar
[57]	Lee T E 2016 Phys. Rev. Lett. 116 133903 Google Scholar
[58]	Kunst F K, Edvardsson E, Budich J C, Bergholtz E J 2018 Phys. Rev. Lett. 121 026808 Google Scholar
[59]	Yao S, Wang Z 2018 Phys. Rev. Lett. 121 086803 Google Scholar
[60]	Yao S, Song F, Wang Z 2018 Phys. Rev. Lett. 121 136802 Google Scholar
[61]	Edvardsson E, Kunst F K, Bergholtz E J 2019 Phys. Rev. B 99 081302 Google Scholar
[62]	Ghatak A, Das T 2019 J. Phys.: Condens. Matter 31 263001 Google Scholar
[63]	Song F, Yao S, Wang Z 2019 Phys. Rev. Lett. 123 170401 Google Scholar
[64]	Song F, Yao S, Wang Z 2019 Phys. Rev. Lett. 123 246801 Google Scholar
[65]	Borgnia D S, Kruchkov A J, Slager R J 2020 Phys. Rev. Lett. 124 056802 Google Scholar
[66]	Xiao L, Deng T, Wang K, Zhu G, Wang Z, Yi W, Xue P 2020 Nat. Phys. 16 761 Google Scholar
[67]	Zhang K, Yang Z, Fang C 2020 Phys. Rev. Lett. 125 126402 Google Scholar
[68]	Yang Z, Zhang K, Fang C, Hu J 2020 Phys. Rev. Lett. 125 226402 Google Scholar
[69]	Okuma N, Sato M 2021 Phys. Rev. Lett. 126 176601 Google Scholar
[70]	Liang Q, Xie D, Dong Z, Li H, Li H, Gadway B, Yi W, Yan B 2022 Phys. Rev. Lett. 129 070401 Google Scholar
[71]	Milburn T J, Doppler J, Holmes C A, Portolan S, Rotter S, Rabl P 2015 Phys. Rev. A 92 052124 Google Scholar
[72]	Zhong Q, Christodoulides D N, Khajavikhan M, Makris K G, El-Ganainy R 2018 Phys. Rev. A 97 020105 Google Scholar
[73]	Zhang K L, Wang P, Song Z 2019 Phys. Rev. A 99 042111 Google Scholar
[74]	Liu S, Ma S, Yang C, Zhang L, Gao W, Xiang Y J, Cui T J, Zhang S 2020 Phys. Rev. Appl. 13 014047 Google Scholar
[75]	Heiss W D 2004 J. Phys. A: Math. Gen. 37 2455 Google Scholar
[76]	Moiseyev N 2011 Non-Hermitian Quantum Mechanics (Cambridge: Cambridge University Press
[77]	Okugawa R, Takahashi R, Yokomizo K 2020 Phys. Rev. B 102 241202 Google Scholar
[78]	Zhang X, Tian Y, Jiang J H, Lu M H, Chen Y F 2021 Nat. Commun. 12 5377 Google Scholar
[79]	Zhang X, Zhang T, Lu M H, Chen Y F 2022 Adv. Phys.: X 7 2109431 Google Scholar
[80]	Deng T S, Yi W 2019 Phys. Rev. B 100 035102 Google Scholar
[81]	Yokomizo K, Murakami S 2019 Phys. Rev. Lett. 123 066404 Google Scholar
[82]	Zhu X, Wang H, Gupta S K, Zhang H, Xie B, Lu M, Chen Y 2020 Phys. Rev. Res. 2 013280 Google Scholar
[83]	Yokomizo K, Murakami S 2020 Prog. Theor. Exp. Phys. 2020 12A102 Google Scholar
[84]	Xiao L, Deng T, Wang K, Wang Z, Yi W, Xue P 2021 Phys. Rev. Lett. 126 230402 Google Scholar
[85]	Wang K, Li T, Xiao L, Han Y, Yi W, Xue P 2021 Phys. Rev. Lett. 127 270602 Google Scholar
[86]	Yokomizo K 2022 Non-Bloch Band Theory of Non Hermitian Systems (Singapore: Springer Nature
[87]	Yokomizo K, Murakami S 2023 Phys. Rev. B 107 195112 Google Scholar
[88]	Shi K, Tian M, Sun F X, Zhang W 2023 Phys. Rev. B 107 205154 Google Scholar
[89]	Zhou H, Lee J Y 2019 Phys. Rev. B 99 235112 Google Scholar
[90]	Kawabata K, Shiozaki K, Ueda M, Sato M 2019 Phys. Rev. X 9 041015 Google Scholar
[91]	Kawabata K, Okuma N, Sato M 2020 Phys. Rev. B 101 195147 Google Scholar
[92]	Bergholtz E J, Budich J C, Kunst F K 2021 Rev. Mod. Phys. 93 015005 Google Scholar
[93]	Liu C H, Zhang K, Yang Z, Chen S 2020 Phys. Rev. Res. 2 043167 Google Scholar
[94]	He P, Liu Y G, Wang J T, Zhu S L 2022 Phys. Rev. A 105 023311 Google Scholar
[95]	Niu X, Li J, Wu S L, Yi X X 2023 Phys. Rev. A 108 032214 Google Scholar
[96]	Nakanishi Y, Sasamoto T 2022 Phys. Rev. A 105 022219 Google Scholar
[97]	Li T, Zhang Y S, Yi W 2022 Phys. Rev. B 105 125111 Google Scholar
[98]	Purkayastha A 2022 Phys. Rev. A 105 062204 Google Scholar
[99]	Roccati F, Palma G M, Ciccarello F, Bagarello F 2022 Open Syst. Inf. Dyn. 29 2250004 Google Scholar
[100]	Niu X, Wang J 2023 arXiv: 2211.04233 [quant-ph
[101]	Liu Y G, Chen S 2023 Phys. Rev. B 107 134307 Google Scholar
[102]	Strang G 2023 Introduction to Linear Algebra (6th Ed.) (Wellesley-Cambridge Press
[103]	Demange G, Graefe E M 2011 J. Phys. A: Math. Theor. 45 025303 Google Scholar
[104]	Rotter I 2009 J. Phys. A: Math. Theor 42 153001 Google Scholar
[105]	Mostafazadeh A 2002 J. Math. Phys. 43 205 Google Scholar
[106]	Mostafazadeh A 2002 J. Math. Phys. 43 3944 Google Scholar
[107]	Xiong Y 2018 J. Phys. Commun. 2 035043 Google Scholar
[108]	Ryu S, Schnyder A P, Furusaki A, Ludwig A W W 2010 New J. Phys 12 065010 Google Scholar
[109]	Xu Z C, Zhou Z, Cheng E, Lang L J, Zhu S L 2022 Sci. China: Phys., Mech. Astron. 65 283011 Google Scholar
[110]	Chen W, Kaya Özdemir Ş, Zhao G, Wiersig J, Yang L 2017 Nature 548 192 Google Scholar
[111]	Wiersig J 2014 Phys. Rev. Lett. 112 203901 Google Scholar
[112]	Kato T 1995 Perturbation Theory for Linear Operators (Berlin, Heidelberg: Springer
[113]	Schindler J, Li A, Zheng M C, Ellis F M, Kottos T 2011 Phys. Rev. A 84 040101 Google Scholar
[114]	Dong Z, Li Z, Yang F, Qiu C W, Ho J S 2019 Nat. Electron. 2 335 Google Scholar
[115]	Zhou B B, Wang L F, Dong L, Huang Q A 2021 J. Phys. Commun. 5 045010 Google Scholar
[116]	Zeng C, Zhu K, Sun Y, Li G, Guo Z, Jiang J, Li Y, Jiang H, Yang Y, Chen H 2021 New J. Phys 23 063008 Google Scholar
[117]	成恩宏, 郎利君 2022 71 160301 Google Scholar Cheng E H, Lang L J 2022 Acta Phys. Sin. 71 160301 Google Scholar
[118]	Hofmann T, Helbig T, Schindler F, Salgo N, Brzezińska M, Greiter M, Kiessling T, Wolf D, Vollhardt A, Kabaši A, Lee C H, Bilušić A, Thomale R, Neupert T 2020 Phys. Rev. Res. 2 023265 Google Scholar
[119]	Liu S, Shao R, Ma S, Zhang L, You O, Wu H, Xiang Y J, Cui T J, Zhang S 2021 Research 2 5608038 Google Scholar
[120]	Stegmaier A, Imhof S, Helbig T, Hofmann T, Lee C H, Kremer M, Fritzsche A, Feichtner T, Klembt S, Höfling S, Boettcher I, Fulga I C, Ma L, Schmidt O G, Greiter M, Kiessling T, Szameit A, Thomale R 2021 Phys. Rev. Lett. 126 215302 Google Scholar
[121]	Zou D, Chen T, He W, Bao J, Lee C H, Sun H, Zhang X 2021 Nat. Commun. 12 7201 Google Scholar
[122]	Wu J, Huang X, Yang Y, Deng W, Lu J, Deng W, Liu Z 2022 Phys. Rev. B 105 195127 Google Scholar
[123]	Zhang W, Di F, Yuan H, Wang H, Zheng X, He L, Sun H, Zhang X 2022 Phys. Rev. B 105 195131 Google Scholar
[124]	Shang C, Liu S, Shao R, Han P, Zang X, Zhang X, Salama K N, Gao W, Lee C H, Thomale R, Manchon A, Zhang S, Cui T J, Schwingenschlögl U 2022 Adv. Sci. 9 2202922 Google Scholar
[125]	Zhang X, Zhang B, Zhao W, Lee C H 2022 arXiv: 2211.09152 [cond-mat.mes-hall
[126]	Zhu P, Sun X Q, Hughes T L, Bahl G 2023 Nat. Commun. 14 720 Google Scholar
[127]	Wu M, Zhao Q, Kang L, Weng M, Chi Z, Peng R, Liu J, Werner D H, Meng Y, Zhou J 2023 Phys. Rev. B 107 064307 Google Scholar
[128]	Kim Y, Park H C, Kyung M, Lee K, Ryu J W, You O, Zhang S, Min B, Park M J 2023 arXiv: 2303.13721 [cond-mat.mes-hall
[129]	Su L, Guo C X, Wang Y, Li L, Ruan X, Du Y, Chen S, Zheng D 2023 Chin. Phys. B 32 038401 Google Scholar
[130]	Yin K, Hao X, Huang Y, Zou J, Ma X, Dong T 2023 Phys. Rev. Applied 20 L021003 Google Scholar
[131]	Ezawa M 2019 Phys. Rev. B 99 121411 Google Scholar
[132]	Zhou B B, Deng W J, Wang L F, Dong L, Huang Q A 2020 Phys. Rev. Appl. 13 064022 Google Scholar
[133]	Schindler J, Lin Z, Lee J M, Ramezani H, Ellis F M, Kottos T 2012 J. Phys. A: Math. Theor. 45 444029 Google Scholar
[134]	Ramezani H, Schindler J, Ellis F M, Günther U, Kottos T 2012 Phys. Rev. A 85 062122 Google Scholar
[135]	Wang T, Fang J, Xie Z, Dong N, Joglekar Y N, Wang Z, Li J, Luo L 2020 Eur. Phys. J. D 74 167 Google Scholar
[136]	Chen W K 2002 The Circuits and Filters Handbook (CRC Press
[137]	Hofmann T, Helbig T, Lee C H, Greiter M, Thomale R 2019 Phys. Rev. Lett. 122 247702 Google Scholar
[138]	Zhang H, Chen T, Li L, Lee C H, Zhang X 2023 Phys. Rev. B 107 085426 Google Scholar
[139]	Yuan H, Zhang W, Zhou Z, Wang W, Pan N, Feng Y, Sun H, Zhang X 2023 Adv. Sci. 2301128 Google Scholar
[140]	Chen P Y, Sakhdari M, Hajizadegan M, Cui Q, Cheng M M C, El-Ganainy R, Alù A 2018 Nat. Electron. 1 297 Google Scholar
[141]	Sakhdari M, Hajizadegan M, Zhong Q, Christodoulides D N, El-Ganainy R, Chen P Y 2019 Phys. Rev. Lett. 123 193901 Google Scholar
[142]	Yin K, Huang Y, Ma C, Hao X, Gao X, Ma X, Dong T 2022 Appl. Phys. Lett. 120 194101 Google Scholar
[143]	Wu F Y 2004 J. Phys. A: Math. Gen. 37 6653 Google Scholar
[144]	Li Z, Wu J, Huang X, Lu J, Li F, Deng W, Liu Z 2020 Appl. Phys. Lett. 116 263501 Google Scholar
[145]	Deng W, Chen T, Zhang X 2022 Phys. Rev. Res. 4 033109 Google Scholar
[146]	Tang C, Yang H, Song L, Yao X, Yan P, Cao Y 2023 Phys. Rev. B 108 035410 Google Scholar
[147]	Lang L J, Weng Y, Zhang Y, Cheng E, Liang Q 2021 Phys. Rev. B 103 014302 Google Scholar
[148]	Chitsazi M, Li H, Ellis F M, Kottos T 2017 Phys. Rev. Lett. 119 093901 Google Scholar
[149]	Su L, Jiang H, Wang Z, Chen S, Zheng D 2023 Phys. Rev. B 107 184108 Google Scholar
[150]	Lee C H, Li L, Gong J 2019 Phys. Rev. Lett. 123 016805 Google Scholar
[151]	Li L, Lee C H, Gong J 2020 Phys. Rev. Lett. 124 250402 Google Scholar
[152]	Yin K, Huang Y, Yin W, Hao X, Ma X, Dong T 2022 Phys. Rev. Appl. 18 064020 Google Scholar
[153]	Zhang M, Sweeney W, Hsu C W, Yang L, Stone A D, Jiang L 2019 Phys. Rev. Lett. 123 180501 Google Scholar
[154]	Kononchuk R, Cai J, Ellis F, Thevamaran R, Kottos T 2022 Nature 607 697 Google Scholar
[155]	Langbein W 2018 Phys. Rev. A 98 023805 Google Scholar

[1]	古燕, 陆展鹏. 非厄米耦合链中的局域化转变. , 2024, 73(19): 197101. doi: 10.7498/aps.73.20240976
[2]	黄泽鑫, 圣宗强, 程乐乐, 曹三祝, 陈华俊, 吴宏伟. 一维非互易声学晶体的非厄米趋肤态操控. , 2024, 73(21): 214301. doi: 10.7498/aps.73.20241087
[3]	任翠翠, 尹相国. 耗散诱导的非厄米边缘爆发重现. , 2023, 72(16): 160501. doi: 10.7498/aps.72.20230338
[4]	杨艳丽, 段志磊, 薛海斌. 非厄米Su-Schrieffer-Heeger链边缘态和趋肤效应依赖的电子输运特性. , 2023, 72(24): 247301. doi: 10.7498/aps.72.20231286
[5]	李家锐, 王梓安, 徐彤彤, 张莲莲, 公卫江. 一维${\cal {PT}}$对称非厄米自旋轨道耦合Su-Schrieffer-Heeger模型的拓扑性质. , 2022, 71(17): 177302. doi: 10.7498/aps.71.20220796
[6]	. 非厄米物理前沿专题编者按. , 2022, 71(13): 130101. doi: 10.7498/aps.71.130101
[7]	高雪儿, 李代莉, 刘志航, 郑超. 非厄米系统的量子模拟新进展. , 2022, 71(24): 240303. doi: 10.7498/aps.71.20221825
[8]	胡洲, 曾招云, 唐佳, 罗小兵. 周期驱动的二能级系统中的准宇称-时间对称动力学. , 2022, 71(7): 074207. doi: 10.7498/aps.70.20220270
[9]	胡洲, 曾招云, 唐佳, 罗小兵. 周期驱动的二能级系统中的准宇称-时间对称动力学. , 2022, 0(0): 0-0. doi: 10.7498/aps.71.20220270
[10]	范辉颖, 罗杰. 非厄密电磁超表面研究进展. , 2022, 71(24): 247802. doi: 10.7498/aps.71.20221706
[11]	侯博, 曾琦波. 非厄米镶嵌型二聚化晶格. , 2022, 71(13): 130302. doi: 10.7498/aps.71.20220890
[12]	刘佳琳, 庞婷方, 杨孝森, 王正岭. 无序非厄米Su-Schrieffer-Heeger中的趋肤效应. , 2022, 71(22): 227402. doi: 10.7498/aps.71.20221151
[13]	陈舒越, 蒋闯, 柯少林, 王兵, 陆培祥. 基于Aharonov-Bohm笼的非厄米趋肤效应抑制现象. , 2022, 71(17): 174201. doi: 10.7498/aps.71.20220978
[14]	邓天舒. 畴壁系统中的非厄米趋肤效应. , 2022, 71(17): 170306. doi: 10.7498/aps.71.20221087
[15]	成恩宏, 郎利君. 非互易Aubry-André 模型的经典电路模拟. , 2022, 71(16): 160301. doi: 10.7498/aps.71.20220219
[16]	胡渝民, 宋飞, 汪忠. 广义布里渊区与非厄米能带理论. , 2021, 70(23): 230307. doi: 10.7498/aps.70.20211908
[17]	孙孔浩, 易为. 非厄米局域拓扑指标的动力学特性. , 2021, 70(23): 230309. doi: 10.7498/aps.70.20211576
[18]	李少华, 杨振军, 陆大全, 胡巍. 厄米-高斯光束在热非局域介质中传输的数值模拟研究. , 2011, 60(2): 024214. doi: 10.7498/aps.60.024214
[19]	黎昌金, 吕百达. 非傍轴部分相干厄米-高斯光束的相干和非相干合成. , 2009, 58(9): 6192-6201. doi: 10.7498/aps.58.6192
[20]	陈增军, 宁西京. 非厄米哈密顿量的物理意义. , 2003, 52(11): 2683-2686. doi: 10.7498/aps.52.2683

计量

文章访问数: 4322
PDF下载量: 220
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

非厄米格点模型的经典电路模拟