具有传质传热及扩散效应的双气泡的相互作用

乌日乐格; 那仁满都拉

doi:10.7498/aps.72.20230863

摘要

利用修正的Keller-Miksis方程与Noble-Abel-Stiffend-Gas状态方程相结合的模型, 研究了超声作用下具有传质传热及扩散效应的双气泡间的相互作用, 并与Mettin等[Mettin R, Akhatov I, Parlitz U, Ohl C D, Lauterborn W 1997 Phys. Rev. E 56 2924]给出的没有传质传热及扩散效应的双气泡间的相互作用进行了比较. 结果表明, 具有传质传热及扩散效应的双气泡间的次Bjerknes力和气泡归一化最大半径都大于没有传质传热及扩散效应的双气泡的相应量. 随着其中一个气泡的初始半径的增大和驱动声压的增大, 两种情况给出的次Bjerknes力的差别逐渐增大, 而随着驱动频率的增大, 两种情况给出的次Bjerknes力的差别逐渐减小. 由此可见, 传质传热和扩散效应对空化气泡间相互作用的次Bjerknes力具有重要影响.

关键词:

Abstract

In this paper, the interaction between the two bubbles with the effects of mass transfer, heat transfer and diffusion was investigated under ultrasonic action by using the model combining the modified Keller-Miksis equation with Noble-Abel-Stiffend-Gas equation of state. The maximum normalized radius of cavitation the bubbles and the secondary Bjerknes force (coefficient) of the interaction between the bubbles are calculated respectively, and compared with the maximum normalized radius of the bubbles and the secondary Bjerknes force (coefficient) in the two bubbles system without the effects of mass transfer, heat transfer and diffusion given by Mettin et al [Mettin R, Akhatov I, Parlitz U, Ohl C D, Lauterborn W 1997 Phys. Rev. E 56 2924]. The results show that the maximum normalized radius of the bubbles and the secondary Bjerknes forces between the bubbles are larger in the two bubbles system with the effects of mass transfer, heat transfer and diffusion than in the two bubbles system without the effects of mass transfer, heat transfer and diffusion. The main reason for this result is that the effects of mass transfer, heat transfer and diffusion can increase the amount of gas contained in the cavitation bubble. With the increase of the initial radius of a certain the bubble in the two bubbles system, the secondary Bjerknes force will increase and the difference between the secondary Bjerknes forces in the two cases will gradually increase. With the increase of the driving sound pressure amplitude, the secondary Bjerknes force will also increase and the difference between the secondary Bjerknes forces in the two cases will also gradually increase. With the increase of the driving frequency, the secondary Bjerknes force will decrease and the difference between the secondary Bjerknes forces in the two cases will also gradually decrease. Therefore, the effects of mass transfer, heat transfer and diffusion have a significant effect on the secondary Bjerknes force of the interaction between cavitation the bubbles, which is an important factor that cannot be ignored. The research results of this article have positive significance for further understanding of the secondary Bjerknes force of the interaction between the two bubbles under ultrasonic action.

Keywords:

cavitation two bubbles /
secondary Bjerknes force /
mass transfer and heat transfer effect /
diffusion effect

作者及机构信息

内蒙古民族大学数理学院, 通辽　028043

通信作者: 那仁满都拉, nrmdlbf@126.com

基金项目: 国家自然科学基金(批准号: 11462019)资助的课题.

Authors and contacts

College of Mathematics and Physics, Inner Mongolia University for Nationalities, Tongliao 028043, China

Corresponding author: Naranmandula, nrmdlbf@126.com

Funds: Project supported by the National Natural Science Foundation of China (Grant No. 11462019).

文章全文 : translate this paragraph

参考文献

[1]	Hilgenfeldt S, Lohse D, Brenner M P 1996 Phys. Fluids 8 2808 Google Scholar
[2]	Yasui K 1997 Phys. Rev. E 56 6750 Google Scholar
[3]	Toegel R, Lohse D 2003 J. Chem. Phys. 118 1863 Google Scholar
[4]	Shen Y, Yasui K, Sun Z C, Mei B, You M Y, Zhu T 2016 Ultrason. Sonochem. 29 394 Google Scholar
[5]	胡静, 林书玉, 王成会, 李锦 2013 62 134303 Google Scholar Hu J, Lin S Y, Wang C H, Li J 2013 Acta Phys. Sin. 62 134303 Google Scholar
[6]	张鹏利, 林书玉, 朱华泽, 张涛 2019 68 134301 Google Scholar Zhang P L, Lin S Y, Zhu H Z, Zhang T 2019 Acta Phys.Sin. 68 134301 Google Scholar
[7]	清河美, 那仁满都拉 2020 69 184301 Google Scholar Qinghim, Naranmandula 2020 Acta Phys. Sin. 69 184301 Google Scholar
[8]	Mettin R, Akhatov I, Parlitz U, Ohl C D, Lauterborn W 1997 Phys. Rev. E 56 2924 Google Scholar
[9]	Doinikov A A 2001 Phys. Rev. E 64 026301 Google Scholar
[10]	Sadighi-Bonabi R, Rezaee N, Ebrahimi H, Mirheydari M 2010 Phys. Rev. E 82 016316 Google Scholar
[11]	Zhang Y N, Zhang Y N, Li S C 2016 Ultrason. Sonochem. 29 129 Google Scholar
[12]	Pandey V 2019 Phys. Rev. E 99 042209 Google Scholar
[13]	Luo J, Niu Z P 2019 Sci. Rep. 9 1352 Google Scholar
[14]	Zhang L L, Chen W Z, Zhang Y Y, Wu Y R, Wang X, Zhao G Y 2020 Chin. Phys. B 29 034303 Google Scholar
[15]	李想, 陈勇, 封皓, 綦磊 2020 69 184703 Google Scholar Li X, Chen Y, Feng H, Qi L 2020 Acta Phys. Sin. 69 184703 Google Scholar
[16]	Shen Y, Zhang L L, Wu Y R, Chen W Z 2021 Ultrason. Sonochem. 73 105535 Google Scholar
[17]	Qin D, Zou Q Q, Lei S, Wang W, Li Z Y 2021 Ultrason. Sonochem. 78 105712 Google Scholar
[18]	Zhang X M, Li F, Wang C H, Mo R Y, Hu J, Guo J Z, Lin S Y 2022 Ultrason. 126 106809 Google Scholar
[19]	王德鑫, 那仁满都拉 2018 67 037802 Google Scholar Wang D X, Naranmandula 2018 Acta Phys.Sin. 67 037802 Google Scholar
[20]	王寻, 黎奥, 周敏, 梁金福, 张泽坤, 吴伟 2022 应用声学 41 735 Wang X, Li A, Zhou M, Liang J F, Zhang Z K, Wu W 2022 J. Appl. Acoust. 41 735
[21]	Yasui K, Iida Y, Tuziuti T, Kozuka T, Towata A 2008 Phys. Rev. E 77 016609 Google Scholar
[22]	Shen Z Z 2020 Chin. Phys. B 29 014304 Google Scholar
[23]	徐珂, 许龙, 周光平 2021 70 194301 Google Scholar Xu K, Xu L, Zhou G P 2021 Acta Phys. Sin. 70 194301 Google Scholar
[24]	Métayer O L, Saurel R 2016 Phys. Fluids 28 046102 Google Scholar
[25]	Toegel R, Gompf B, Pecha R, Lohse D 2000 Phys. Rev. Lett. 85 3165 Google Scholar
[26]	Longwell P A, Olin J B, Sage B H 1958 Ind. Eng. Chem. Chem. Eng. Data Series 3 175 Google Scholar
[27]	Hirschfelder J A, Curtiss C F, Bird R B 1954 Molecular Theory of Gases and Liquids (New York: Wiley) pp293–302
[28]	Dehane A, Merouani S, Hamdaoui O, Alghyamah A 2021 Ultrason. Sonochem. 73 105511 Google Scholar
[29]	Yasui K, Tuziuti T, Kanematsu W 2016 Phys. Rev. E 94 013106 Google Scholar
[30]	Jishnu C R, Salih A M 2018 Fluid Phase Equilib. 483 182 Google Scholar
[31]	Yasui K 1995 J. Acoust. Soc. Am. 98 2772 Google Scholar

施引文献

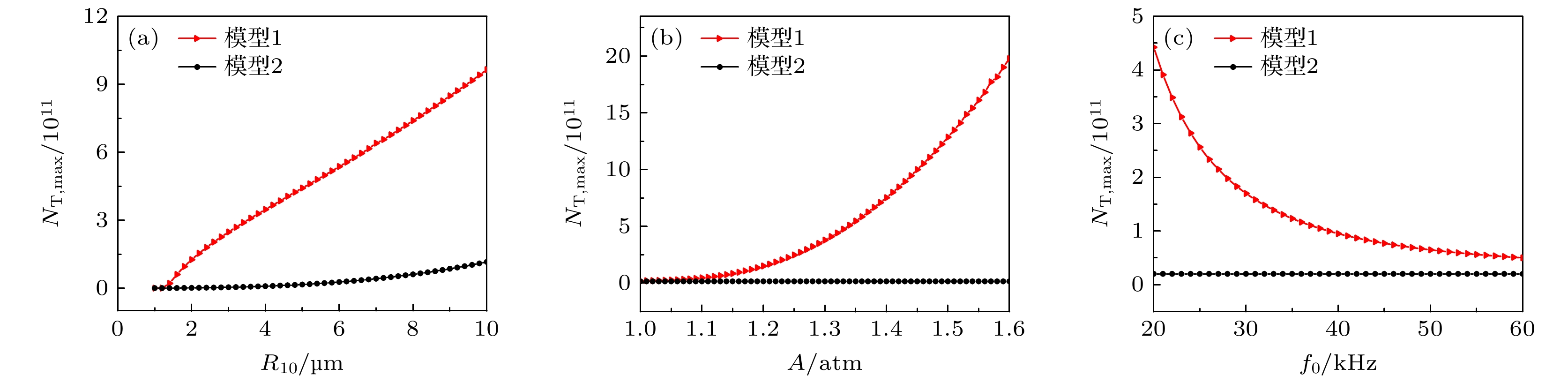
图 1 空化气泡内气体最大总分子数$ N_\mathrm{\rm{T}, max} $的变化 (a)当$R_{20}=5 \;\text{μm}$, $ A=1.32 P_{0} $, $ f_{0}=20\;\mathrm{kHz} $时, $ N_\mathrm{\rm{T}, max} $随气泡1初始半径的变化; (b)当$ R_{10}=R_{20}=5 \;\text{μm} $, $ f_{0}=20\;\mathrm{kHz} $时, $ N_\mathrm{\rm{T}, max} $随驱动声压的变化; (c)当$ R_{10}=R_{20}=5 \;\text{μm} $, $ A=1.32 P_{0} $ 时, $ N_\mathrm{\rm{T}, max} $随驱动频率的变化

Fig. 1. Change of the maximum total molecular number $ N_\mathrm{\rm{T}, max} $ of gas in cavitation bubble: (a) $ N_\mathrm{\rm{T}, max} $ changes with the initial radius of bubble 1 at $ R_{20}=5\; \text{μm} $, $ A=1.32 P_{0} $, $ f_{0}=20\;\mathrm{kHz} $; (b) $ N_\mathrm{\rm{T}, max} $ changes with driving sound pressure at $ R_{10}=R_{20}=5 \;\text{μm} $, $ f_{0}=20\;\mathrm{kHz} $; (c) $ N_\mathrm{\rm{T}, max} $ changes with driving frequency at $ R_{10}=R_{20}=5 \;\text{μm} $, $ A=1.32 P_{0} $.

下载: 全尺寸图片幻灯片

图 2 空化气泡归一化最大半径和次Bjerknes力系数随气泡1初始半径的变化 (a)归一化最大半径; (b)次Bjerknes力系数

Fig. 2. Maximum normalized radius of cavitation the bubbles and the secondary Bjerknes force coefficient change with the initial radius of bubble 1: (a) Maximum normalized radius; (b) the secondary Bjerknes force coefficient

下载: 全尺寸图片幻灯片

图 3 空化气泡归一化最大半径和次Bjerknes力系数随驱动声压的变化 (a)归一化最大半径; (b)次Bjerknes力系数

Fig. 3. Maximum normalized radius of cavitation the bubbles and the secondary Bjerknes force coefficient change with driving sound pressure: (a) Maximum normalized radius; (b) the secondary Bjerknes force coefficient

下载: 全尺寸图片幻灯片

图 4 空化气泡归一化最大半径和次Bjerknes力系数随驱动频率的变化 (a) 归一化最大半径; (b) 次Bjerknes力系数

Fig. 4. Maximum normalized radius of cavitation the bubbles and the secondary Bjerknes force coefficient change with driving frequency: (a) Maximum normalized radius; (b) the secondary Bjerknes force coefficient

下载: 全尺寸图片幻灯片

表 1 模型1的相关物理参数

Table 1. Related physical parameters of model 1

参数	值	单位
液体密度 $ \rho_{0} $	998	$ \mathrm{kg{\cdot} m^{-3}} $
黏性系数 μ	0.001	$ \mathrm{Pa{\cdot} s} $
表面张力 σ	0.0725	$ \mathrm{N{\cdot} m^{-1}} $
环境温度 $ T_{\mathrm{0}} $	300	$ \mathrm{K} $
液体热容比 $ \gamma_\mathrm{l} $	1.19	$ - $
液体热容 $ C_\mathrm{V, l} $	3610	$ \mathrm{J{\cdot} kg^{-1} {\cdot} K^{-1}} $
饱和蒸汽压 $ P_\mathrm{v} $	$ 2.3381\times 10^{3} $	$ \mathrm{Pa} $
液体分子共体积 $ b_\mathrm{l} $	$ 6.7145\times 10^{-4} $	$ \mathrm{m^3{\cdot} kg^{-1}} $
液体压力常数 $ B_\mathrm{l} $	$ 6.2239\times 10^8 $	$ \mathrm{Pa} $
气体压力常数 $ B_\mathrm{g} $	0	$ \mathrm{Pa} $
气体摩尔质量 $ M_{\mathrm{H_{2}O}} $	0.018	$ \mathrm{kg{\cdot} mol^{-1}} $
气体摩尔质量 $ M_{\mathrm{Ar}} $	0.04	$ \mathrm{kg{\cdot} mol^{-1}} $
阿伏伽德罗常数 $ N_{\mathrm{A}} $	$ 6.023\times 10^{23} $	$ \mathrm{mol^{-1}} $
玻尔斯曼常数 $ k_{\mathrm{B}} $	$ 1.38\times 10^{-23} $	$ \mathrm{J{\cdot} K^{-1}} $
环境压力 $ P_{\mathrm{0}} $	$ 10^{5} $	$ \mathrm{Pa} $
气泡间距 $d_{ij}$	$ 10^{-3} $	$ \mathrm{m} $

下载: 导出CSV

表 2 模型2的相关物理参数

Table 2. Related physical parameters of model 2

参数	值	单位
液体密度 $ \rho_{0} $	998	$ \mathrm{kg{\cdot} m^{-3}} $
黏性系数 μ	0.001	$ \mathrm{Pa{\cdot} s} $
表面张力 σ	0.0725	$ \mathrm{N{\cdot} m^{-1}} $
环境压力 $ P_{\mathrm{0}} $	$ 1\times 10^{5} $	$ \mathrm{Pa} $
气体热容比 $ \gamma_\mathrm{g} $	1.67	$ - $
液体中的声速 $ C_\mathrm{l} $	1500	$ \mathrm{m{\cdot} s^{-1}} $
气泡间距 $d_{ij}$	$ 1\times 10^{-3} $	$ \mathrm{m} $

下载: 导出CSV

map

[1]	Hilgenfeldt S, Lohse D, Brenner M P 1996 Phys. Fluids 8 2808 Google Scholar
[2]	Yasui K 1997 Phys. Rev. E 56 6750 Google Scholar
[3]	Toegel R, Lohse D 2003 J. Chem. Phys. 118 1863 Google Scholar
[4]	Shen Y, Yasui K, Sun Z C, Mei B, You M Y, Zhu T 2016 Ultrason. Sonochem. 29 394 Google Scholar
[5]	胡静, 林书玉, 王成会, 李锦 2013 62 134303 Google Scholar Hu J, Lin S Y, Wang C H, Li J 2013 Acta Phys. Sin. 62 134303 Google Scholar
[6]	张鹏利, 林书玉, 朱华泽, 张涛 2019 68 134301 Google Scholar Zhang P L, Lin S Y, Zhu H Z, Zhang T 2019 Acta Phys.Sin. 68 134301 Google Scholar
[7]	清河美, 那仁满都拉 2020 69 184301 Google Scholar Qinghim, Naranmandula 2020 Acta Phys. Sin. 69 184301 Google Scholar
[8]	Mettin R, Akhatov I, Parlitz U, Ohl C D, Lauterborn W 1997 Phys. Rev. E 56 2924 Google Scholar
[9]	Doinikov A A 2001 Phys. Rev. E 64 026301 Google Scholar
[10]	Sadighi-Bonabi R, Rezaee N, Ebrahimi H, Mirheydari M 2010 Phys. Rev. E 82 016316 Google Scholar
[11]	Zhang Y N, Zhang Y N, Li S C 2016 Ultrason. Sonochem. 29 129 Google Scholar
[12]	Pandey V 2019 Phys. Rev. E 99 042209 Google Scholar
[13]	Luo J, Niu Z P 2019 Sci. Rep. 9 1352 Google Scholar
[14]	Zhang L L, Chen W Z, Zhang Y Y, Wu Y R, Wang X, Zhao G Y 2020 Chin. Phys. B 29 034303 Google Scholar
[15]	李想, 陈勇, 封皓, 綦磊 2020 69 184703 Google Scholar Li X, Chen Y, Feng H, Qi L 2020 Acta Phys. Sin. 69 184703 Google Scholar
[16]	Shen Y, Zhang L L, Wu Y R, Chen W Z 2021 Ultrason. Sonochem. 73 105535 Google Scholar
[17]	Qin D, Zou Q Q, Lei S, Wang W, Li Z Y 2021 Ultrason. Sonochem. 78 105712 Google Scholar
[18]	Zhang X M, Li F, Wang C H, Mo R Y, Hu J, Guo J Z, Lin S Y 2022 Ultrason. 126 106809 Google Scholar
[19]	王德鑫, 那仁满都拉 2018 67 037802 Google Scholar Wang D X, Naranmandula 2018 Acta Phys.Sin. 67 037802 Google Scholar
[20]	王寻, 黎奥, 周敏, 梁金福, 张泽坤, 吴伟 2022 应用声学 41 735 Wang X, Li A, Zhou M, Liang J F, Zhang Z K, Wu W 2022 J. Appl. Acoust. 41 735
[21]	Yasui K, Iida Y, Tuziuti T, Kozuka T, Towata A 2008 Phys. Rev. E 77 016609 Google Scholar
[22]	Shen Z Z 2020 Chin. Phys. B 29 014304 Google Scholar
[23]	徐珂, 许龙, 周光平 2021 70 194301 Google Scholar Xu K, Xu L, Zhou G P 2021 Acta Phys. Sin. 70 194301 Google Scholar
[24]	Métayer O L, Saurel R 2016 Phys. Fluids 28 046102 Google Scholar
[25]	Toegel R, Gompf B, Pecha R, Lohse D 2000 Phys. Rev. Lett. 85 3165 Google Scholar
[26]	Longwell P A, Olin J B, Sage B H 1958 Ind. Eng. Chem. Chem. Eng. Data Series 3 175 Google Scholar
[27]	Hirschfelder J A, Curtiss C F, Bird R B 1954 Molecular Theory of Gases and Liquids (New York: Wiley) pp293–302
[28]	Dehane A, Merouani S, Hamdaoui O, Alghyamah A 2021 Ultrason. Sonochem. 73 105511 Google Scholar
[29]	Yasui K, Tuziuti T, Kanematsu W 2016 Phys. Rev. E 94 013106 Google Scholar
[30]	Jishnu C R, Salih A M 2018 Fluid Phase Equilib. 483 182 Google Scholar
[31]	Yasui K 1995 J. Acoust. Soc. Am. 98 2772 Google Scholar

[1]	许龙, 汪尧. 双泡耦合声空化动力学过程模拟. , 2023, 72(2): 024303. doi: 10.7498/aps.72.20221571
[2]	黄晨阳, 李凡, 田华, 胡静, 陈时, 王成会, 郭建中, 莫润阳. 空化场中大气泡对空化泡振动的抑制效应分析. , 2023, 72(6): 064302. doi: 10.7498/aps.72.20221955
[3]	李凡, 张先梅, 田华, 胡静, 陈时, 王成会, 郭建中, 莫润阳. 液体薄层中环链状空化泡云结构稳定性分析. , 2022, 71(8): 084303. doi: 10.7498/aps.71.20212257
[4]	秦对, 邹青钦, 李章勇, 王伟, 万明习, 冯怡. 组织内包膜微泡声空化动力学及其力学效应分析. , 2021, 70(15): 154701. doi: 10.7498/aps.70.20210194
[5]	李想, 陈勇, 封皓, 綦磊. 声波激励下管路轴向分布双气泡动力学特性分析. , 2020, 69(18): 184703. doi: 10.7498/aps.69.20200546
[6]	清河美, 那仁满都拉. 空化多泡中大气泡对小气泡空化效应的影响. , 2019, 68(23): 234302. doi: 10.7498/aps.68.20191198
[7]	王德鑫, 那仁满都拉. 耦合双泡声空化特性的理论研究. , 2018, 67(3): 037802. doi: 10.7498/aps.67.20171805
[8]	马艳, 林书玉, 徐洁, 唐一璠. 非球形效应对强声场中次Bjerknes力的影响. , 2017, 66(1): 014302. doi: 10.7498/aps.66.014302
[9]	郑新奇, 沈俊, 胡凤霞, 孙继荣, 沈保根. 磁热效应材料的研究进展. , 2016, 65(21): 217502. doi: 10.7498/aps.65.217502
[10]	马艳, 林书玉, 鲜晓军. 次Bjerknes力作用下气泡的体积振动和散射声场. , 2016, 65(1): 014301. doi: 10.7498/aps.65.014301
[11]	姚洪斌, 郑雨军. NaI分子的非绝热效应. , 2011, 60(12): 128201. doi: 10.7498/aps.60.128201
[12]	卢义刚, 吴雄慧. 双泡超声空化计算分析. , 2011, 60(4): 046202. doi: 10.7498/aps.60.046202
[13]	崔虎, 张冰志, 佘卫龙. 非相干耦合的亮和暗光伏空间孤子对的偏转特性. , 2010, 59(3): 1823-1830. doi: 10.7498/aps.59.1823
[14]	董浩, 任敏, 张磊, 邓宁, 陈培毅. 电流驱动磁化翻转中的热效应. , 2009, 58(10): 7176-7182. doi: 10.7498/aps.58.7176
[15]	朱樟明, 郝报田, 钱利波, 钟波, 杨银堂. 考虑通孔效应和边缘传热效应的纳米级互连线温度分布模型. , 2009, 58(10): 7130-7135. doi: 10.7498/aps.58.7130
[16]	颜利芬, 王红成, 张冰志, 佘卫龙. 光伏暗孤子和灰孤子的自偏转. , 2007, 56(8): 4627-4634. doi: 10.7498/aps.56.4627
[17]	颜利芬, 王红成, 佘卫龙. 扩散效应对光伏孤子相互作用的影响. , 2006, 55(10): 5257-5262. doi: 10.7498/aps.55.5257
[18]	张建华, 孟庆苗, 李传安. 广义球对称带电蒸发黑洞的量子热效应和非热效应. , 1996, 45(2): 177-184. doi: 10.7498/aps.45.177
[19]	沈鸿元. 正交晶系YAP晶体的热效应. , 1981, 30(8): 1075-1099. doi: 10.7498/aps.30.1075
[20]	夏蒙棼. 随机磁场中的反常扩散效应. , 1981, 30(9): 1275-1278. doi: 10.7498/aps.30.1275

计量

文章访问数: 2135
PDF下载量: 60
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板