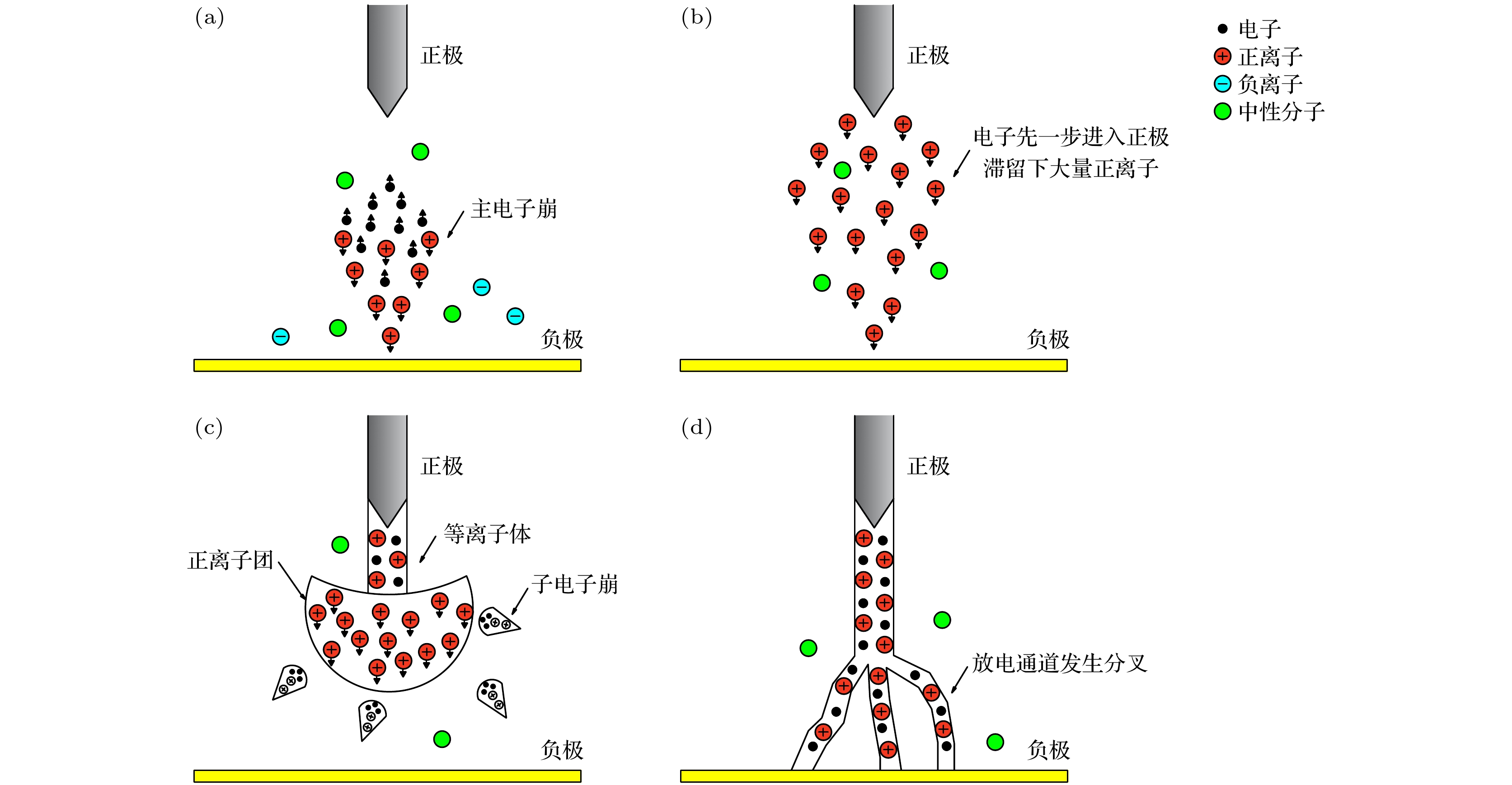
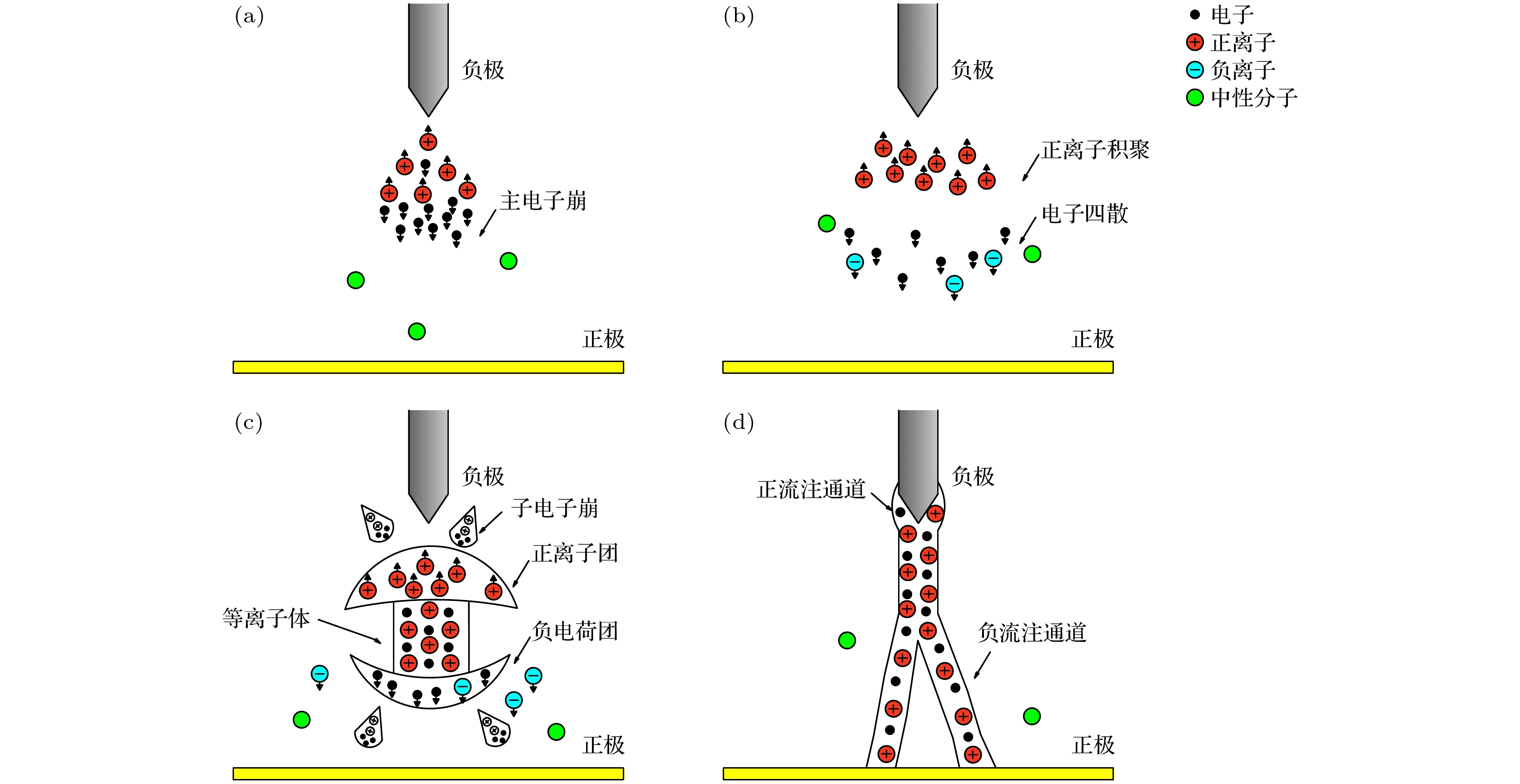
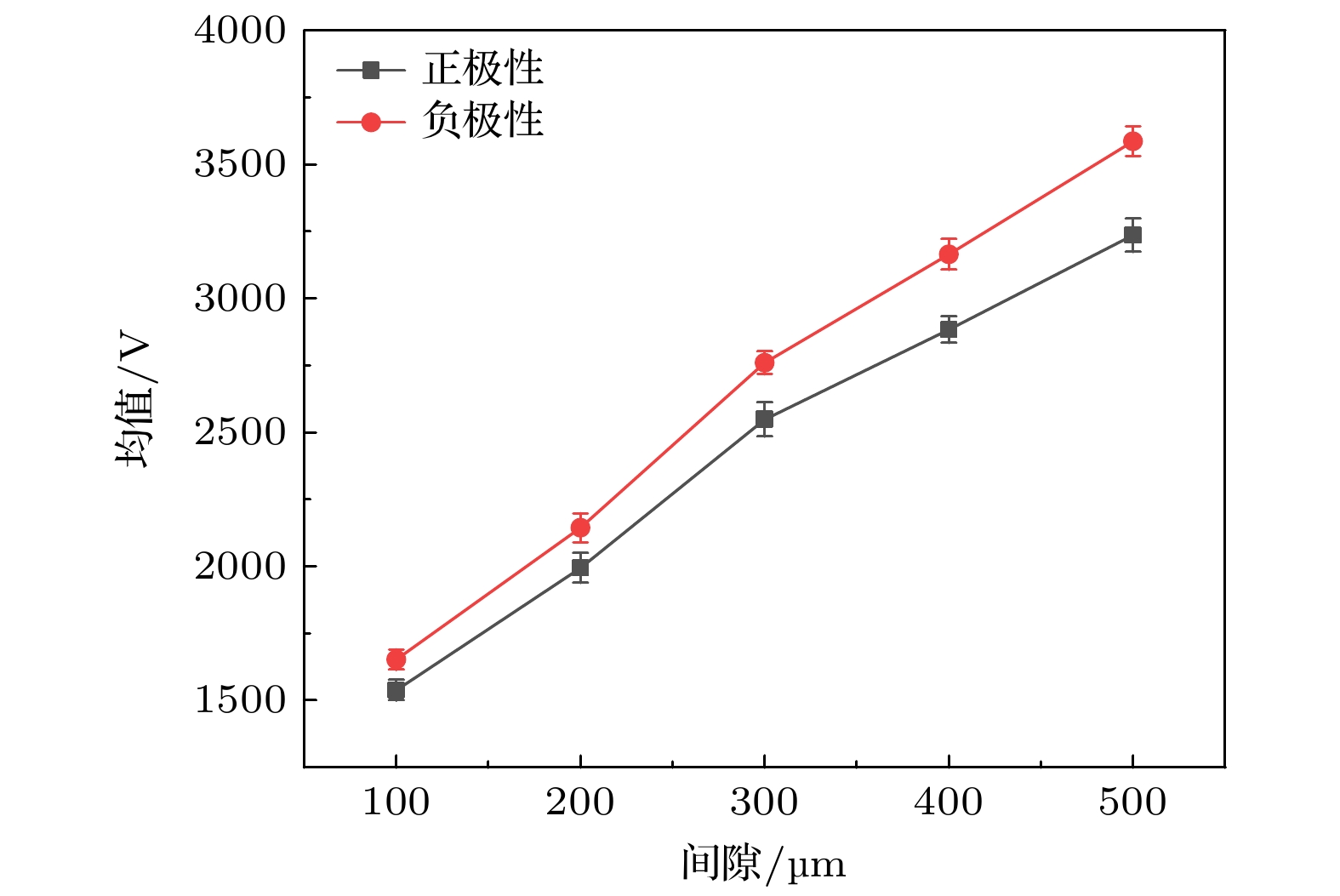
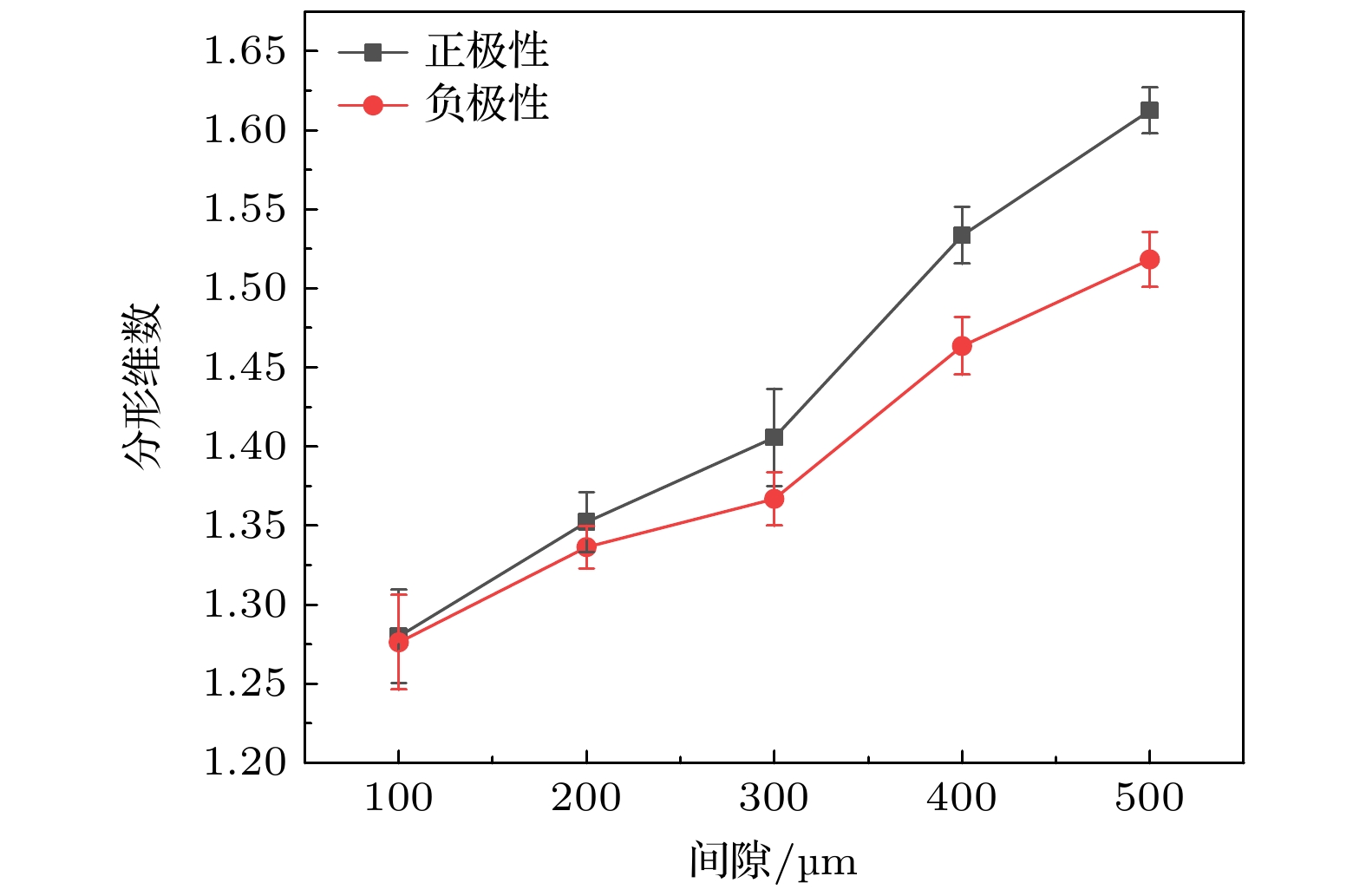
-
为研究亚毫米间隙下流注放电特性, 本文搭建了大气压下100—500 μm间隙下的正负极性流注放电实验系统以及图像采集系统, 采集100—500 μm间隙下正负极性流注放电的起始击穿电压与击穿图像并使用Matlab计算实验放电图像的分形维数. 实验分析发现100—500 μm间隙下的空气击穿放电依旧符合流注理论, 且正、负极性流注的击穿电压与放电图像分形维数的极性效应明显, 流注理论中空间电荷与光电离对放电通道曲折程度与覆盖范围的影响随着间隙增大而增大, 且在300 μm时发生跃变. 使用Matlab基于分形理论的WZ (Wiesmann-Zeller)模型建立500 μm间隙下正、负极性流注放电分形仿真, 发现发展概率指数η与分形维数成反比, 且同放电条件下放电发展概率指数η在正极性流注中相对于负极性流注要更小.In order to study the characteristics of streamer discharge in sub-millimeter gap, an experimental system and an image acquisition system of positive and negative polarity streamer discharge in the gap of 100–500 μm at atmospheric pressure are built, and the initial breakdown voltages and breakdown images of positive and negative polarity streamer discharge in a gap range of 100–500 μm are collected, and the fractal dimension of the experimental discharge images is calculated by Matlab. The experimental analysis shows that the air breakdown discharge in the gap range of 100–500 μm still conforms to the stream theory, and the polarity effect between the breakdown voltage of positive and negative streamers and the fractal dimension of the discharge image is obvious. The influence of space charge and photoionization on the meandering degree and coverage of the discharge channel in stream theory increase with the increase of the gap, and jump at 300 μm. The fractal simulation of positive and negative streamer discharge with a gap of 500 μm is established by using WZ (Wiesmann-Zeller) model based on fractal theory in Matlab. It is found that the development probability index η is inversely proportional to the fractal dimension, and that the η is smaller in positive streamer than in negative streamer under the same discharge condition.
-
Keywords:
- submillimeter gap /
- stream theory /
- polarity effect /
- fractal dimension
[1] 欧阳吉庭, 张宇, 秦宇 2016 高电压技术 42 673
Google Scholar
Ouyang J T, Zhang Y, Qin Y 2016 High Voltage Eng. 42 673
Google Scholar
[2] 孟国栋, 成永红, 酉小广, 吴锴 2012 西安交通大学学报 46 106
Google Scholar
Meng G D, Cheng Y H, You X G, Wu K 2012 J. Xi’an Jiaotong Univ. 46 106
Google Scholar
[3] Meek J M 1940 Phys. Rev. 57 722
Google Scholar
[4] 刘典, 夏胜国 2015 高电压技术 41 282
Google Scholar
Liu D, Xia S G 2015 High Volt. Eng. 41 282
Google Scholar
[5] 程文馨 2018 硕士学位论文 (南京: 南京航空航天大学)
Cheng W X 2018 M. S. Thesis (Nanjing: Nanjing University of Aeronautics and Astronautics
[6] 王成江, 涂鸣麟, 方洋洋, 沈书林, 李亚莎 2019 绝缘材料 52 57
Google Scholar
Wang C J, Tu M L, Fang Y Y, Shen S L, Li Y S 2019 Insul. Mater. 52 57
Google Scholar
[7] Ono R, Komuro A 2019 J. Phys. D: Appl. Phys. 53 035202
Google Scholar
[8] Starikovskiy A Y, Aleksandrov N L 2020 Plasma Sources Sci. Technol. 29 075004
Google Scholar
[9] Sosnin E A, Panarin V A, Skakun V S, Baksht E Kh, Kuznetsov V S, Sorokin D A 2022 Russ. Phys. J. 65 1194
Google Scholar
[10] 赵志航, 魏新劳, 姚远航, 朱博, 聂洪岩, 李毅恒 2022 中国电机工程学报 43 4034
Google Scholar
Zhao Z H, Wei X L, Yao Y H, Zhu B, Nie H Y, Li Y H 2022 Chin. Soc. Electr. Eng. 43 4034
Google Scholar
[11] 蒋兴良, 吴建国, 任晓东, 胡建林, 张志劲 2023 高电压技术 49 1743
Google Scholar
Jiang X L, Wu J G, Ren X D, Hu J L, Zhang Z J 2023 High Voltage Eng. 49 1743
Google Scholar
[12] Niemeyer L, Pietronero L, Wiesmann H J 1984 Phys. Rev. Lett. 52 1033
Google Scholar
[13] Wiesmann H J, Zeller H R A 1986 J. Appl. Phys. 60 1770
Google Scholar
[14] Amarasinghe D, Sonnadara U 2009 J. Sci. 6 57
Google Scholar
[15] 薛福明 2012 硕士学位论文 (哈尔滨: 哈尔滨理工大学)
Xue F M 2012 M. S. Thesis (Harbin: Harbin University of Science and Technology
[16] 郑殿春, 丁宁, 沈湘东, 赵大伟, 郑秋平, 魏红庆 2016 65 024703
Google Scholar
Zheng D C, Ding N, Shen X D, Zhao D W, Zheng Q P, Wei H Q 2016 Acta Phys. Sin. 65 024703
Google Scholar
[17] 赵大帅, 孙志, 孙兴, 孙怀得, 韩柏 2021 70 205207
Google Scholar
Zhao D S, Sun Z, Sun X, Sun H D, Han B 2021 Acta Phys. Sin. 70 205207
Google Scholar
[18] Geng J H, Wang Q S, Liu X M, Wang P, Lü F C, Ding Y J 2022 Plasma Sci. Technol. 24 095402
Google Scholar
[19] 王江涛, 杨建梅 2013 复杂系统与复杂性科学 10 1
Google Scholar
Wang J T, Yang J M 2013 Complex Syst. Complex. Sci. 10 1
Google Scholar
[20] Canny J 1986 IEEE Trans. Pattern Anal. Mach. Intell. 8 679
Google Scholar
[21] 高电压试验技术 局部放电测量 第3页
High Voltage Test Techniques-Partial Discharge Measurements p3
[22] Zhang Q Z, Zhang L, Yang D Z 2021 Plasma Processes and Polym. 18 200234
Google Scholar
[23] Zhang Y, Wang H, Zhang Y, Bogaerts A 2017 Plasma Sources Sci. Technol. 26 54002
Google Scholar
[24] 于亮2005 硕士学位论文 (重庆: 重庆大学)
Yu L 2005 M. S. Thesis (Chongqing: Chongqing University
-
图 4 100—500 μm正极性流注起始击穿图像
Fig. 4. Initial breakdown image of 100–500 μm positive polarity streamer.
图 5 100—500 μm负极性流注起始击穿图像
Fig. 5. Initial breakdown image of 100–500 μm negative polarity streamer.
图 6 亚毫米间隙正极性流注原理图
Fig. 6. Schematic diagram of positive polarity streamer with submillimeter gap.
图 7 亚毫米间隙负极性流注原理图
Fig. 7. Schematic diagram of negative polarity streamer with sub-millimeter gap.
图 8 实验所得100—500 μm正负极性起始流注击穿电压平均值
Fig. 8. Average breakdown voltage of 100–500 μm streamer with positive and negative polarity obtained by experiment.
图 9 实验所得100—500 μm正负极性流注击穿图像分形维数平均值
Fig. 9. Average fractal dimension of 100–500 μm experimental streamer breakdown images with positive and negative polarity.
图 11 正极性流注分形仿真图 (a) η = 0.30, D = 1.5789; (b) η = 0.20, D = 1.6011; (c) η = 0.19, D = 1.6167; (d) η = 0.10, D = 1.6663
Fig. 11. Fractal simulation diagram of positive polarity streamer: (a) η = 0.30, D = 1.5789; (b) η = 0.20, D = 1.6011; (c) η = 0.19, D = 1.6167; (d) η = 0.10, D = 1.6663.
图 12 负极性流注分形仿真图 (a) η = 0.50, D = 1.4975; (b) η = 0.45, D = 1.5110; (c) η = 0.43, D = 1.5183; (d) η = 0.40, D = 1.5284
Fig. 12. Fractal simulation diagram of negative polarity streamer: (a) η = 0.50, D = 1.4975; (b) η = 0.45, D = 1.5110; (c) η = 0.43, D = 1.5183; (d) η = 0.40, D = 1.5284.
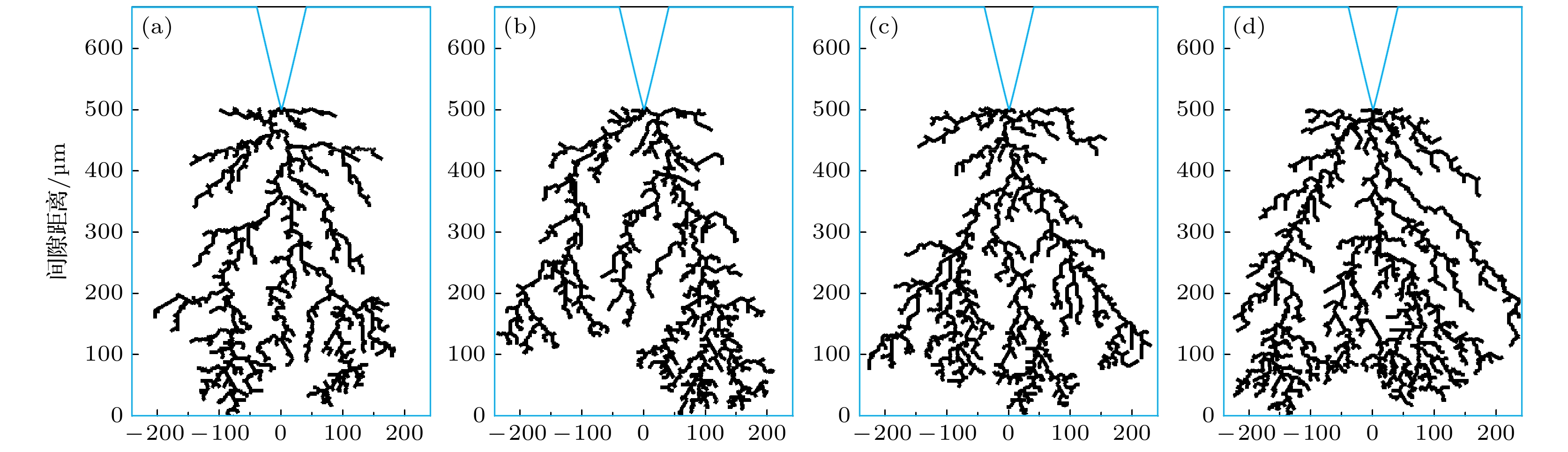
表 1 正极性流注放电仿真分形维数
Table 1. Fractal dimension of positive streamer discharge simulation.
仿真次数 η = 0.30 η = 0.21 η = 0.20 η = 0.19 η = 0.18 η = 0.17 η = 0.1 1 1.5849 1.5613 1.5994 1.6176 1.5873 1.6211 1.6914 2 1.5884 1.6155 1.646 1.63 1.6268 1.6728 1.6663 3 1.5621 1.5735 1.6011 1.6053 1.6206 1.6123 1.6741 4 1.5682 1.6116 1.6181 1.6075 1.6163 1.5858 1.6555 5 1.5789 1.5929 1.5841 1.5903 1.5925 1.6484 1.6622 6 1.5263 1.6176 1.5756 1.6116 1.6288 1.6591 1.6314 7 1.6026 1.6219 1.6245 1.6009 1.6594 1.6038 1.6611 8 1.5504 1.6228 1.6321 1.6632 1.6523 1.6382 1.6605 9 1.5839 1.6297 1.604 1.5704 1.6654 1.6235 1.6744 10 1.5549 1.596 1.5976 1.6264 1.5959 1.6446 1.6181 均值 1.5701 1.6043 1.6083 1.6123 1.6245 1.631 1.6595 95%置信区间 [1.4916,
1.6486][1.5241,
1.6845][1.5278,
1.6887][1.5317,
1.6929][1.5433,
1.7058][1.5494,
1.7125][1.5765,
1.7425]
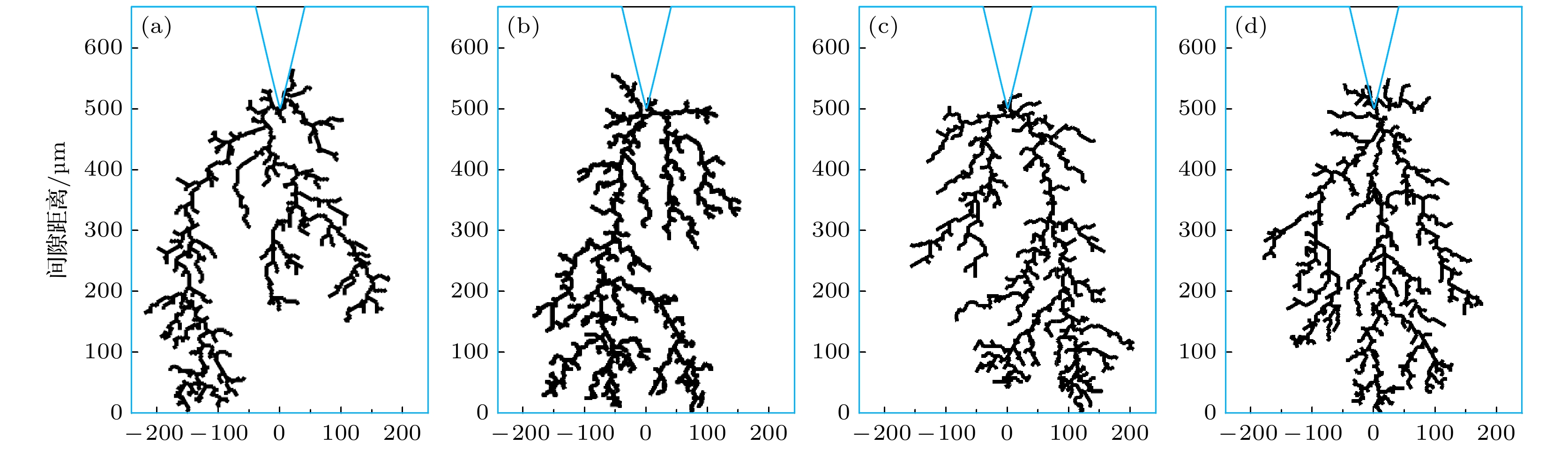
下载: 导出CSV
表 2 负极性流注放电仿真分形维数
Table 2. Fractal dimension of negative streamer discharge simulation.
仿真次数 η = 0.5 η = 0.45 η = 0.44 η = 0.43 η = 0.42 η = 0.41 η = 0.4 1 1.5312 1.4781 1.5484 1.5183 1.5366 1.5127 1.5607 2 1.4896 1.5559 1.5114 1.4996 1.5098 1.5177 1.5479 3 1.4376 1.5340 1.5087 1.5635 1.4537 1.5584 1.5257 4 1.4896 1.5277 1.5196 1.5344 1.5282 1.4970 1.4987 5 1.4839 1.5680 1.4784 1.461 1.5824 1.5003 1.5432 6 1.4708 1.511 1.5049 1.506 1.5222 1.5226 1.4779 7 1.5265 1.4753 1.5449 1.4963 1.4911 1.5190 1.5441 8 1.5140 1.4610 1.5194 1.5434 1.5344 1.5356 1.5306 9 1.5179 1.5242 1.5127 1.5615 1.5222 1.5711 1.5238 10 1.4975 1.5224 1.5222 1.5112 1.5434 1.5168 1.5284 均值 1.4959 1.5158 1.5171 1.5195 1.5224 1.5251 1.5281 95%置信区间 [1.4211,
1.5707][1.4400,
1.5915][1.4412,
1.5929][1.4435,
1.5955][1.4463,
1.5985][1.4489,
1.6014][1.4517,
1.6045]
下载: 导出CSV
-
[1] 欧阳吉庭, 张宇, 秦宇 2016 高电压技术 42 673
Google Scholar
Ouyang J T, Zhang Y, Qin Y 2016 High Voltage Eng. 42 673
Google Scholar
[2] 孟国栋, 成永红, 酉小广, 吴锴 2012 西安交通大学学报 46 106
Google Scholar
Meng G D, Cheng Y H, You X G, Wu K 2012 J. Xi’an Jiaotong Univ. 46 106
Google Scholar
[3] Meek J M 1940 Phys. Rev. 57 722
Google Scholar
[4] 刘典, 夏胜国 2015 高电压技术 41 282
Google Scholar
Liu D, Xia S G 2015 High Volt. Eng. 41 282
Google Scholar
[5] 程文馨 2018 硕士学位论文 (南京: 南京航空航天大学)
Cheng W X 2018 M. S. Thesis (Nanjing: Nanjing University of Aeronautics and Astronautics
[6] 王成江, 涂鸣麟, 方洋洋, 沈书林, 李亚莎 2019 绝缘材料 52 57
Google Scholar
Wang C J, Tu M L, Fang Y Y, Shen S L, Li Y S 2019 Insul. Mater. 52 57
Google Scholar
[7] Ono R, Komuro A 2019 J. Phys. D: Appl. Phys. 53 035202
Google Scholar
[8] Starikovskiy A Y, Aleksandrov N L 2020 Plasma Sources Sci. Technol. 29 075004
Google Scholar
[9] Sosnin E A, Panarin V A, Skakun V S, Baksht E Kh, Kuznetsov V S, Sorokin D A 2022 Russ. Phys. J. 65 1194
Google Scholar
[10] 赵志航, 魏新劳, 姚远航, 朱博, 聂洪岩, 李毅恒 2022 中国电机工程学报 43 4034
Google Scholar
Zhao Z H, Wei X L, Yao Y H, Zhu B, Nie H Y, Li Y H 2022 Chin. Soc. Electr. Eng. 43 4034
Google Scholar
[11] 蒋兴良, 吴建国, 任晓东, 胡建林, 张志劲 2023 高电压技术 49 1743
Google Scholar
Jiang X L, Wu J G, Ren X D, Hu J L, Zhang Z J 2023 High Voltage Eng. 49 1743
Google Scholar
[12] Niemeyer L, Pietronero L, Wiesmann H J 1984 Phys. Rev. Lett. 52 1033
Google Scholar
[13] Wiesmann H J, Zeller H R A 1986 J. Appl. Phys. 60 1770
Google Scholar
[14] Amarasinghe D, Sonnadara U 2009 J. Sci. 6 57
Google Scholar
[15] 薛福明 2012 硕士学位论文 (哈尔滨: 哈尔滨理工大学)
Xue F M 2012 M. S. Thesis (Harbin: Harbin University of Science and Technology
[16] 郑殿春, 丁宁, 沈湘东, 赵大伟, 郑秋平, 魏红庆 2016 65 024703
Google Scholar
Zheng D C, Ding N, Shen X D, Zhao D W, Zheng Q P, Wei H Q 2016 Acta Phys. Sin. 65 024703
Google Scholar
[17] 赵大帅, 孙志, 孙兴, 孙怀得, 韩柏 2021 70 205207
Google Scholar
Zhao D S, Sun Z, Sun X, Sun H D, Han B 2021 Acta Phys. Sin. 70 205207
Google Scholar
[18] Geng J H, Wang Q S, Liu X M, Wang P, Lü F C, Ding Y J 2022 Plasma Sci. Technol. 24 095402
Google Scholar
[19] 王江涛, 杨建梅 2013 复杂系统与复杂性科学 10 1
Google Scholar
Wang J T, Yang J M 2013 Complex Syst. Complex. Sci. 10 1
Google Scholar
[20] Canny J 1986 IEEE Trans. Pattern Anal. Mach. Intell. 8 679
Google Scholar
[21] 高电压试验技术 局部放电测量 第3页
High Voltage Test Techniques-Partial Discharge Measurements p3
[22] Zhang Q Z, Zhang L, Yang D Z 2021 Plasma Processes and Polym. 18 200234
Google Scholar
[23] Zhang Y, Wang H, Zhang Y, Bogaerts A 2017 Plasma Sources Sci. Technol. 26 54002
Google Scholar
[24] 于亮2005 硕士学位论文 (重庆: 重庆大学)
Yu L 2005 M. S. Thesis (Chongqing: Chongqing University
下载:
计量
- 文章访问数: 2708
- PDF下载量: 73
- 被引次数: 0
