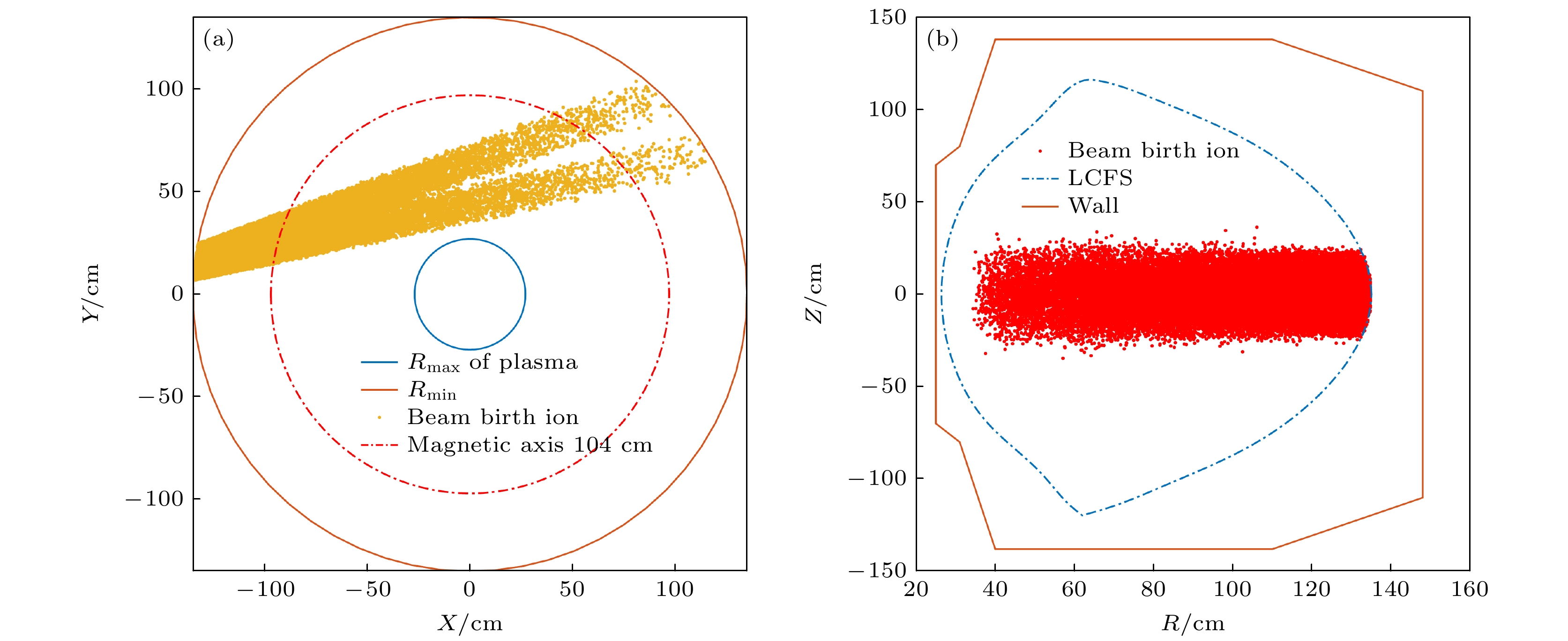
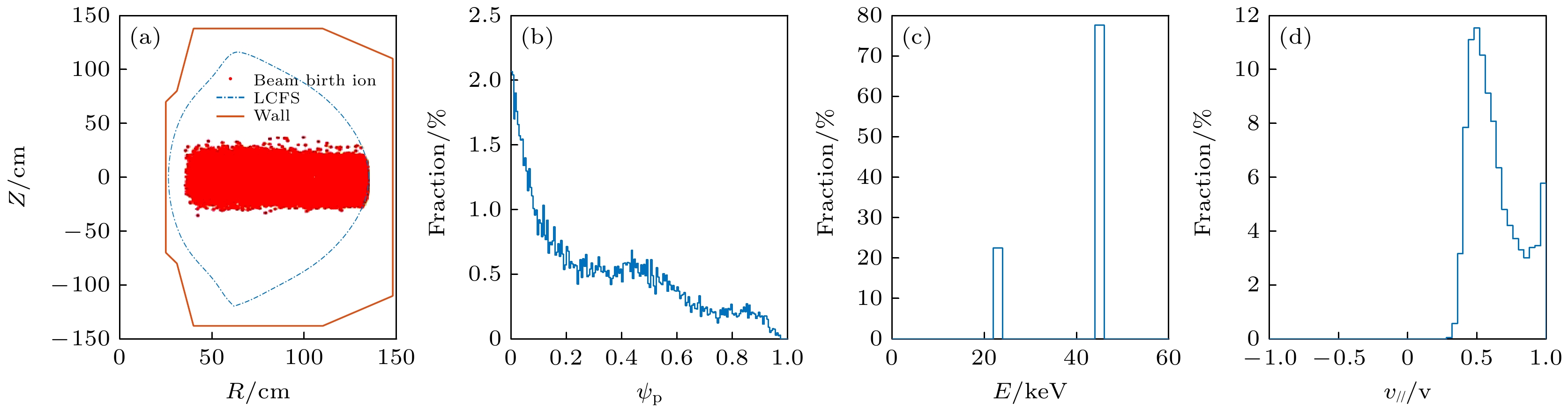
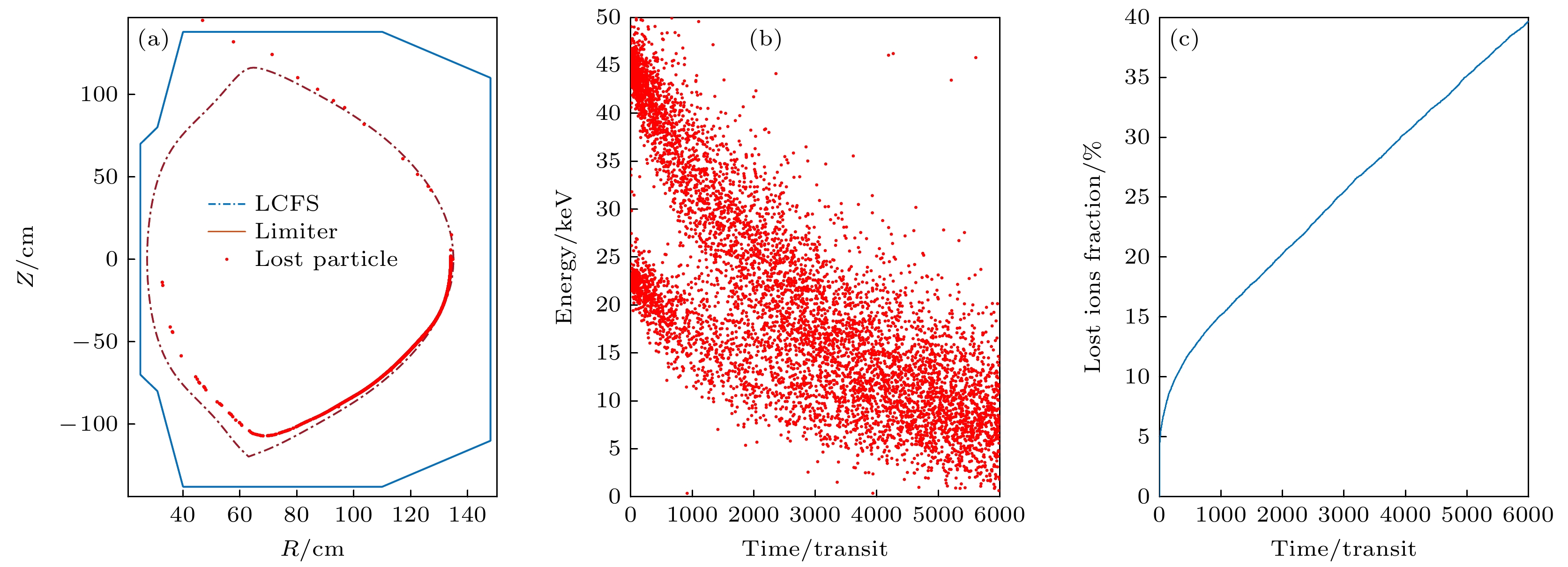
-
EXL-50U装置高参数等离子体的实现对中性束注入(NBI)加热的依赖非常敏感, 期望NBI快离子约束良好并通过碰撞慢化把能量传给背景等离子体. 本文基于集成模拟给出的平衡位形、快离子分布和装置波纹度数据对快离子波纹损失开展了模拟研究. 发现快离子波纹损份额约为37%, 局域热斑约 0.6 MW/m2, 对装置实验运行来说不可接受. 其优化方案包括移动等离子体位置和加FI(铁素体钢插件)降低波纹度, 增大 Ip (等离子体电流)以及优化 NBI 角度. 结果显示必须控制波纹度分布且增大 Ip 到 600 kA 以上, 才能使快离子损失降低到 3%—4%, 局域热斑降低一个量级. 本文总结了装置设计时快离子波纹损失评估的方法, 包括相空间快离子分布和波纹损失区重合度, 全要素慢化时间尺度粒子跟踪. 还总结了降低波纹损失的工程和物理途径, 为集成模拟迭代优化和装置运行提供模拟支持.Realization of high performance plasma of EXL-50U is very sensitive to NBI (neutral beam injection) heating, and it is expected that the fast ions of NBI are confined well and their energy is transferred to the background plasma by collision moderating. In this paper, the loss of fast ion ripple is simulated based on the equilibrium configuration, fast ion distribution and device waviness data given by the integrated simulation. It is found that the loss fraction of fast ion ripple is about 37%, and the local hot spot is about 0.6 MW/m2, which is unacceptable for the experimental operation of the device. The optimization method includes moving the plasma position and adding FI (ferritic steel plug-in) to reduce the ripple degree, increasing the Ip (plasma current) and optimizing the NBI injection angle. The results show that the ripple distribution must be controlled and the Ip must be increased to more than 600 kA, so that the fast ion loss can be reduced to 3%–4% and the local heat spot can be reduced by an order of magnitude. In this paper, the evaluation methods of fast ion ripple loss in device design are summarized, including the fast ion distribution in phase space, the overlap degree of ripple loss area, and the particle tracking on the time scale of total factor slowing down. The engineering and physical ways to reduce ripple loss are also summarized to provide simulation support for integrated simulation iterative optimization and plant operation.
[1] Chen J L, Jian X, Chan V S, Li Z Y, Deng Z, Li G Q, Guo W F, Shi N, Chen X, CFETR Physics Team 2017 Plasma Phys. Control. Fusion 59 075005
Google Scholar
[2] Gorelenkov N N, Pinches S D, Toi K 2014 Nucl. Fusion 54 125001
Google Scholar
[3] 郝保龙, 陈伟, 蔡辉山, 李国强, 王丰, 吴斌, 王进芳, 陈佳乐, 王兆亮, 高翔, Chan Vincent, CFETR TEAM 2020 中国科学:物理学 力学 天文学 50 065201
Google Scholar
Hao B L, Chen W, Cai H S, Li G Q, Wang F, Wu B, Wang J F, Chen J L, Wang Z L, Gao X, Chan V, CFETR TEAM 2020 Sci. Sin. -Phys. Mech. Astron. 50 065201
Google Scholar
[4] Wu B, Hao B L, White R B, Wang J F, Zang Q, Han X F, Hu C D 2017 Plasma Phys. Control. Fusion 59 025004
Google Scholar
[5] Podesta M, Gorelenkova M, Gorelenkov N N, White R B 2017 Plasma Phys. Control. Fusion 59 095008
Google Scholar
[6] Taimourzadeh S, Bass E M, Chen Y, Collins C, Gorelenkov N N, Könies A, Lu Z X, Spong D A, Todo Y, Austin M E, Bao J, Biancalani A, Borchardt M, Bottino A, Heidbrink W W, Kleiber R, Lin Z, Mishchenko A, Shi L, Varela J, Waltz R E, Yu G, Zhang W L, Zhu Y 2019 Nucl. Fusion 59 066006
Google Scholar
[7] Duarte V N, Lestz J B, Gorelenkov N N, White R B 2023 Phys. Rev. Lett. 130 105101
Google Scholar
[8] Pankin A, McCune D, Andre R, Bateman G, Kritz A 2004 Comput. Phys. Commun. 159 157
Google Scholar
[9] White R B, Rutherford P H, Colestock P, Bussac M N 1988 Phys. Rev. Lett. 60 2038
Google Scholar
[10] White R B 2014 The Theory of Toroidally Confined Plasmas (3rd Ed.) (Singapore: World Scientific Publishing Company
[11] White R B, Boozer A H, Hay R 1982 Phys. Fluids 25 575
Google Scholar
[12] Redi M H, White R B, Batha S H, Levinton F M, McCune D C 1997 Phys. Plasmas 4 4001
Google Scholar
[13] Redi M H, Zarnstorff M C, White R B, Budny R V, Janos A C, Owens D K, Schivell J F, Scott S D, Zweben S J 1995 Nucl. Fusion 35 1191
Google Scholar
[14] Redi M H, Budny R V, McCune D C, Miller C O, White R B 1996 Phys. Plasmas 3 3037
Google Scholar
[15] 郝保龙, 陈伟, 李国强, 王晓静, 王兆亮, 吴斌, 臧庆, 揭银先, 林晓东, 高翔, CFETR Team 2021 70 115201
Google Scholar
Hao B L, Chen W, Li G Q, Wang X J, Wang Z L, Wu B, Zang Q, Jie Y X, Lin X D, Gao X, CFETR Team 2021 Acta Phys. Sin. 70 115201
Google Scholar
[16] Wesson J Tokamaks 2011 (New York: Oxford University Press
[17] Hao B L, White R B, Gao X, Li G Q, Chen W, Wang X J, Wu B, Wu M Q, Zhu X, Lin X D, Jie Y X, Zang Q, Li J G, Wan Y X, CFETR Physics Team 2021 Nucl. Fusion 61 046035
Google Scholar
[18] Boozer A H, Kuo-Petravic G, 1981 Phys. Fluids 24 851
Google Scholar
[19] Kramer G J, McLean A, Brooks N, Budny R V, Chen X, Heidbrink W W, Kurki-Suonio T, Nazikian R, Koskela T, Schaffer M J, Shinohara K, Snipes J A, Van Zeeland M A 2013 Nucl. Fusion 53 123018
Google Scholar
[20] ITER Physics Expert Group on Energetic Particles, Heating and Current Drive and ITER Physics Basis Editors 1999 Nucl. Fusion 39 2495
Google Scholar
[21] Tobita K, Nakayama T, Konovalov S V, Sato M 2003 Plasma Phys. Control. Fusion 45 133
Google Scholar
[22] Pinches S D, Chapman I T, Lauber P W, Oliver H J C, Sharapov S E, Shinohara K, Tani K 2015 Phys. Plasmas 22 021807
Google Scholar
-
图 1 EXL-50U集成模拟设计中背景电子密度ne、温度Te和离子温度分布Ti
Fig. 1. Distribution of bulk electron density ne, electron temperature Te and bulk ion temperature Ti in EXL-50U integrated modeling.
图 2 EXL-50U纵场波纹度分布 (a) 解析函数实现值; (b) 工程设计值
Fig. 2. Distribution of toroidal field ripple perturbation amplitude in EXL-50U: (a) Ripple data by analytical equation; (b) engineering data in design.
图 4 EXL-50U装置波纹度不同R截面工程数据和数值拟合结果对比 (a) R = 0.5 m; (b) R = 0.7 m; (c) R = 0.9 m; (d) R = 1.1 m
Fig. 4. Ripple comparison between engineering design and fitting curve in different R plane of EXL-50U: (a) R = 0.5 m; (b) R = 0.7 m; (c) R = 0.9 m; (d) R = 1.1 m.
图 3 EXL-50U装置波纹度不同Z截面工程数据和数值拟合结果对比 (a) Z = 0 m; (b) Z = 0.3 m; (c) Z = 0.6 m; (d) Z = 0.9 m
Fig. 3. Ripple comparison between engineering design and fitting curve in different Z plane of EXL-50U: (a) Z = 0 m; (b) Z = 0.3 m; (c) Z = 0.6 m; (d) Z = 0.9 m.
图 5 EXL-50U上NBI快离子初始分布的粒子空间位置俯视图(a)和极向投影(b)
Fig. 5. Initial distribution of beam ions in EXL-50U: (a) Bird’s view; (b) poloidal cross section.
图 6 Orbit程序中读入的NBI快离子初始分布函数 (a) RZ空间分布; (b)粒子密度的极向磁通分布; (c)能量分布; (d) pitch角分布
Fig. 6. Initial distribution of NBI fast ions read by Orbit code: (a) Particle location in RZ coordinate; (b) particle density distribution in poloidal flux; (c) energy distribution; (d) pitch angle distribution.
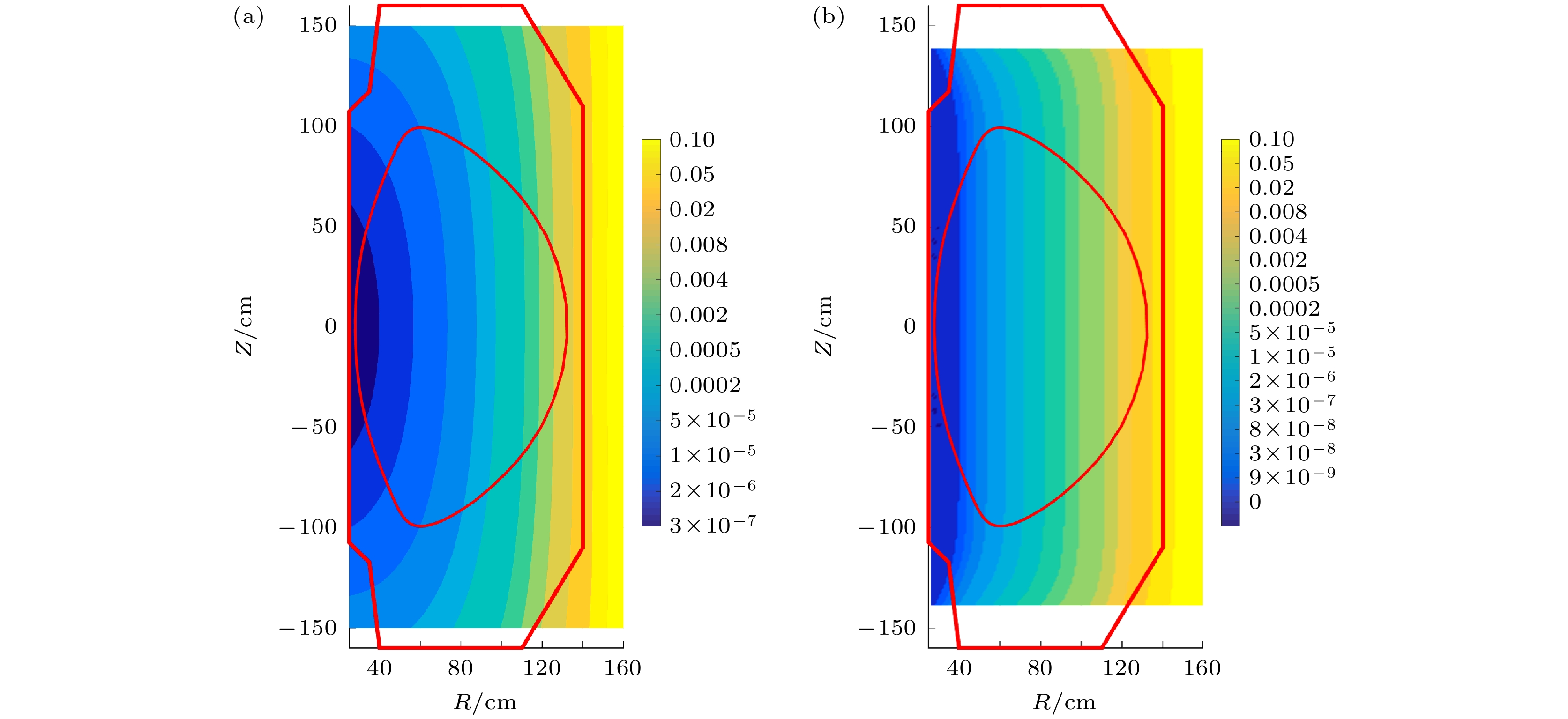
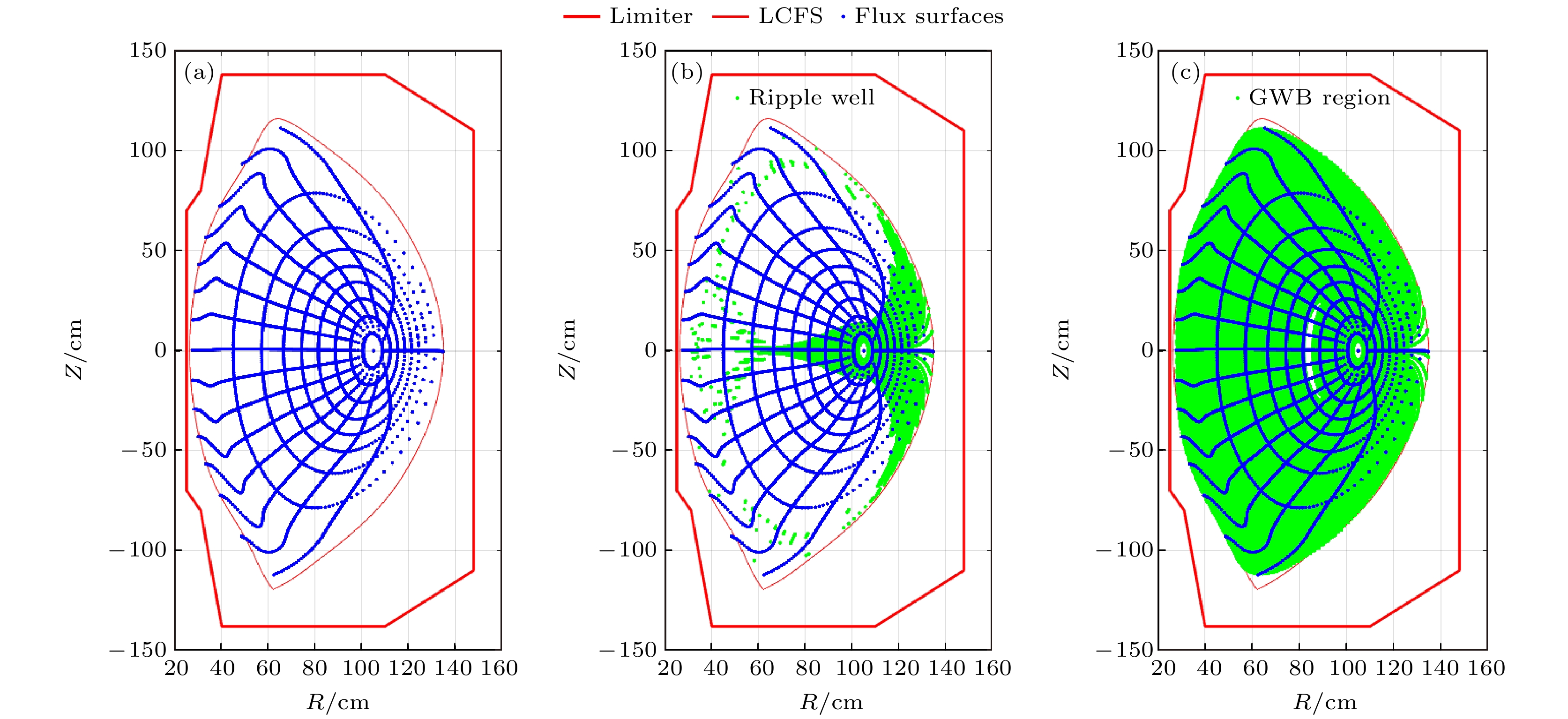
图 7 EXL-50U集成模拟中使用的平衡位形和波纹场重建后的波纹损失区 (a) Boozer坐标系磁面; (b)波纹磁阱俘获损失区, 香蕉粒子转折点位于此区即损失; (c)无碰撞波纹随机扩散损失区, GWB判据
Fig. 7. Equilibrium and ripple loss region in EXL-50U integrated modeling: (a) Magnetic flux surface in Boozer coordinate; (b) ripple well loss region, where banana tips in here will lost; (c) collisionless ripple stochastic diffusion region, plot with GWB criterion.
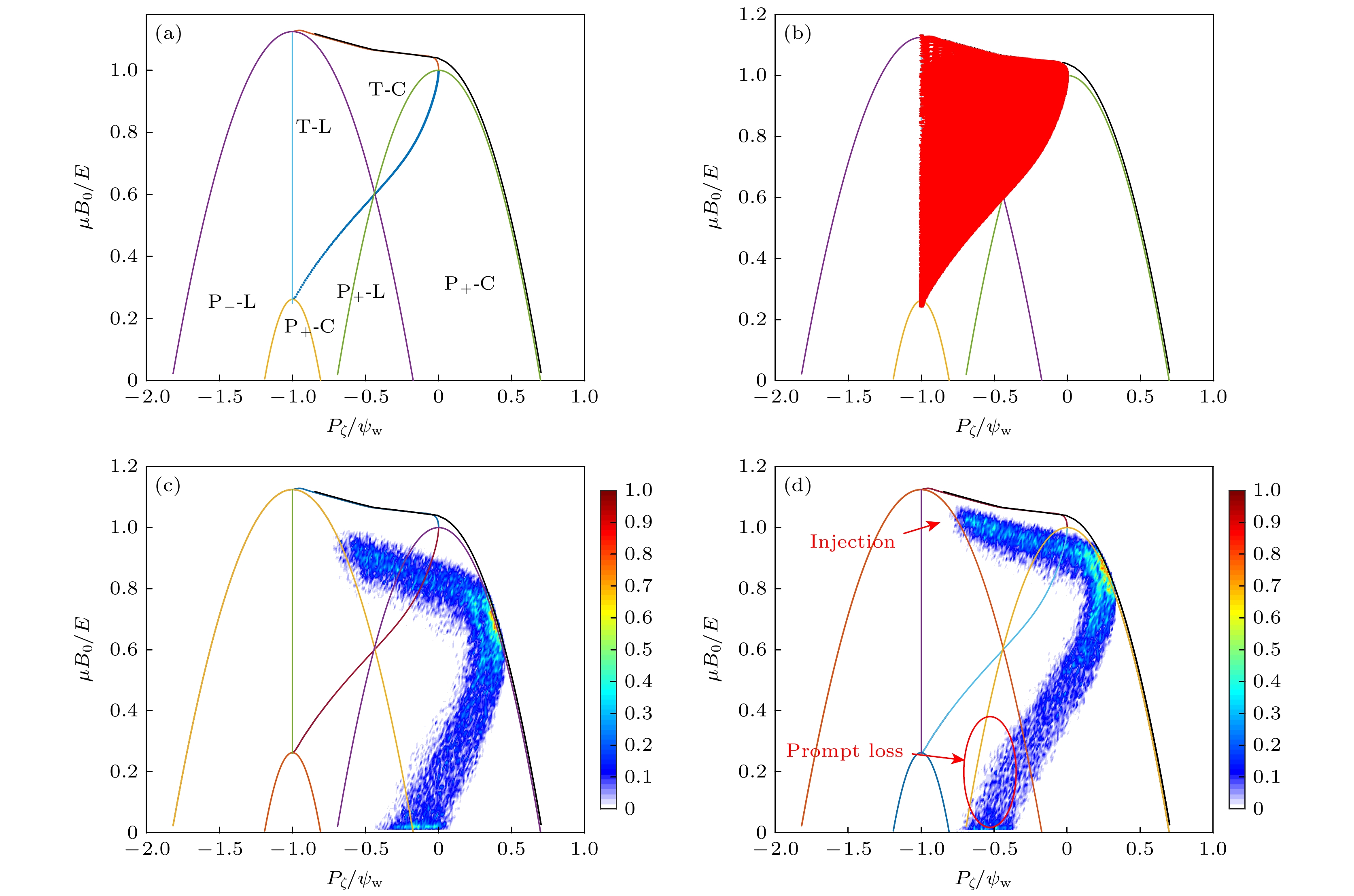
图 8 (a) 初始能量固定时, 在(
$ {P_\zeta }, {{\mu {B_0}} \mathord{\left/ {\vphantom {{\mu {B_0}} E}} \right. } E} $ )平面NBI快离子相空间的轨道类型分布; (b) 波纹损失区(随机波纹扩散GWB判据); (c) co-tang (较切向)的NBI快离子初始分布; (d) co-perp (较垂直) 的NBI快离子初始分布Fig. 8. (a) Orbit classification in the plane of (
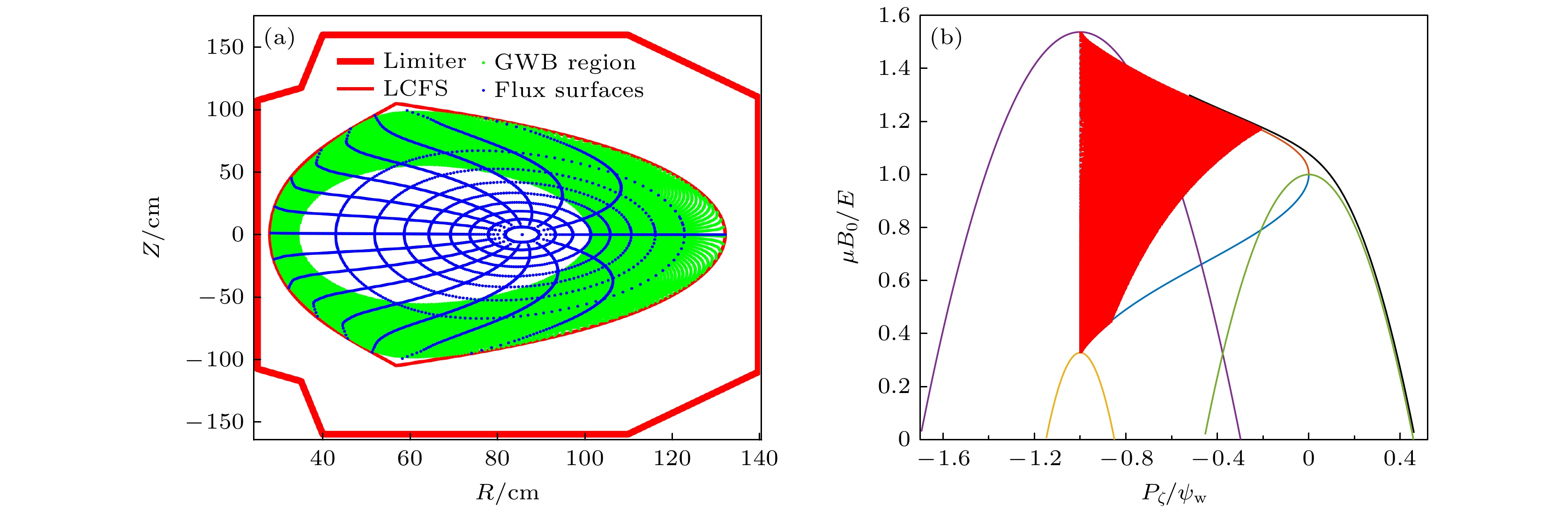
$ {P_\zeta }, {{\mu {B_0}} \mathord{\left/ {\vphantom {{\mu {B_0}} E}} \right. } E} $ ) with fixed initial energy of NBI fast ions; (b) region of stochastic ripple diffusion by GWB criterion; (c) co-tang initial NBI fast ion distribution; (d) co-perp initial NBI fast ion distribution.
图 9 一个慢化时间后NBI快离子分布信息 (a) RZ空间分布; (b)径向坐标统计; (c)末态粒子能量; (d) pitch角统计
Fig. 9. NBI fast ions distribution after one slowing down time calculation: (a) Particle location in RZ coordinate; (b) poloidal flux distribution; (c) particle energy in final time; (d) pitch angle distribution in final time.
图 10 Co-perp快离子分布下的(a)损失粒子极向位置分布, (b)损失时间和能量记录, (c)损失份额的随时演化
Fig. 10. (a) Poloidal distribution of lost particle, (b) lost time and energy record, (c) time evolution of loss fraction for co-perp beam ion distribution.
图 11 一个慢化时间后损失的NBI快离子局域沉积在LCFS处得到的热负荷
Fig. 11. Heat load at the last closed flux surface due to NBI fast ions loss after a slowing down time.
图 12 LCFS的Rmax移动到1.32 m时的波纹损失区(GWB判据) (a) RZ平面; (b) (
$ {P_\zeta }, {{\mu {B_0}} \mathord{\left/ {\vphantom {{\mu {B_0}} E}} \right. } E} $ )平面Fig. 12. The GWB stochastic ripple diffusion regime: (a) RZ poloidal cross section; (b) in the plane of (
$ {P_\zeta }, {{\mu {B_0}} \mathord{\left/ {\vphantom {{\mu {B_0}} E}} \right. } E} $ ).
图 13 500 kA平衡位形LCFS Rmax～1.16时的(a), (c)波纹磁阱区和(b), (d)随机波纹扩散区 (a), (b)单独TF波纹场; (c), (d) TF+FI波纹场
Fig. 13. Ripple well regime (a), (c) and stochastic ripple diffusion regime (b), (d) in 500 kA, Rmax～1.16 m equilibrium: (a), (b) TF ripple; (c), (d) TF+FI ripple.
图 14 不同NBI注入角度下的NBI沉积路径的极向截面 (a)切向半径Rtang = 0.8 m, 离子源垂直中平面抬升Zelev = 0 m; (b)切向半径Rtang = 1.0 m, 离子源垂直中平面抬升Zelev = 0.6 m
Fig. 14. Cross section of NBI deposition trajectory with different NBI geometry: (a) Beam tangency radius Rtang = 0.8 m, elevation of beam ion source above midplane Zelev = 0 m; (b) beam tangency radius Rtang = 1.0 m, elevation of beam ion source above midplane Zelev = 0.6 m.
表 1 EXL-50U与其他托卡马克装置主机参数对比
Table 1. Main parameters comparison of EXL-50U and other tokomak facilities.
参数 CFETR ITER HL-2M EAST EXL-50U 磁轴场强
$ {B_{T0}} $/T6.5 5.3 3 2 0.6–0.8 等离子体大
半径$ {R_0} $/m7.2 6.2 1.78 1.9 0.9 等离子体小
半径a/m2.2 2.0 0.62 0.5 0.45 等离子体电流
$ {I_{\text{p}}} $/MA14 15 3 1 0.5–1 纵场磁体
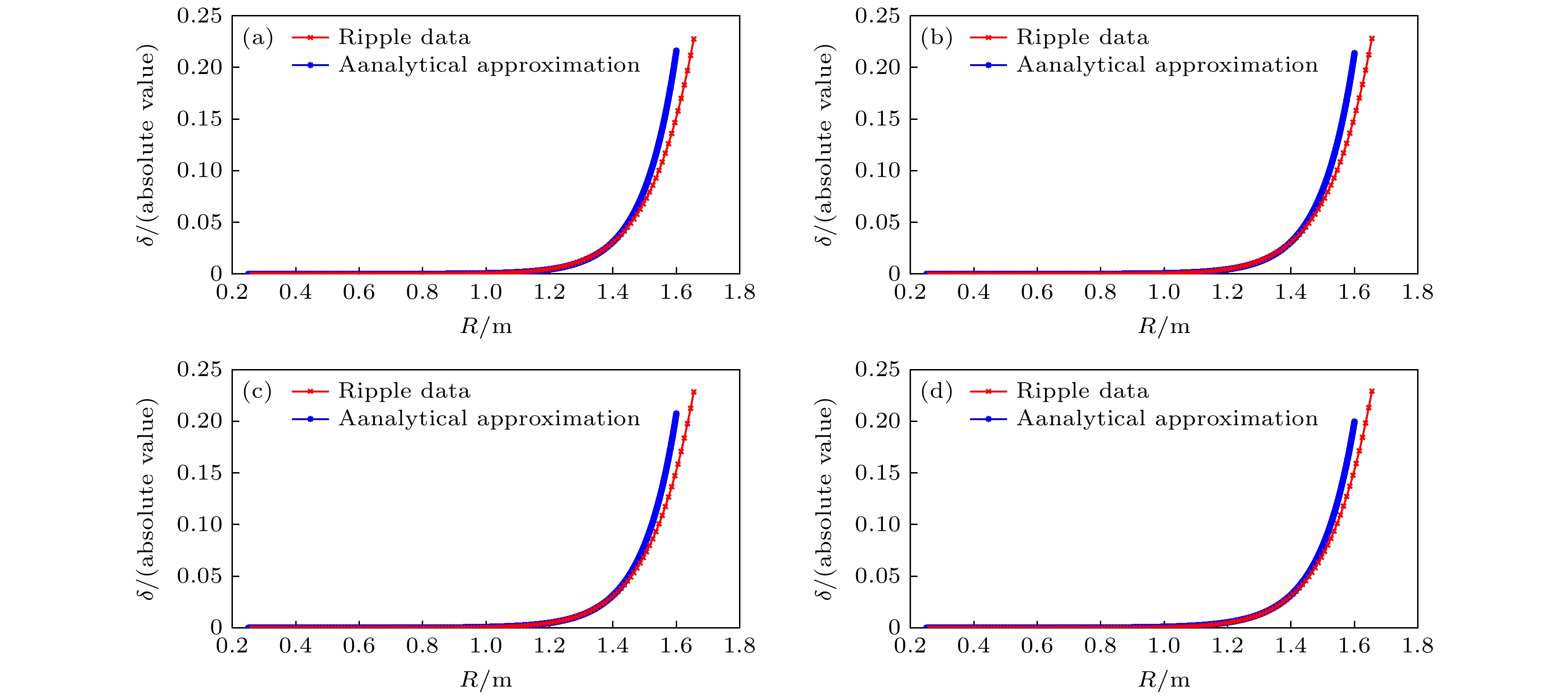
柄数 N16 18 20 16 12 
下载: 导出CSV
表 2 EXL-50U与其他托卡马克装置纵场波纹数据拟合结果对比
Table 2. Ripple field fitting parameters comparison of EXL-50U and other tokomak facilities.
Item CFETR ITER EAST EXL-50U $ {\delta _0} $ 1.57 × 10–5 3.75 × 10–6 1.26 × 10–4 4.19 × 10–8 R0 = a + bZ 2 (m) 6 + 0.062Z 2 6.75 – 0.034 Z 2 1.71 – 0.18 Z 2 1.77 × 10–3 + 0.106 Z 2 brip 0.021 0.26 0.26 0.297 wrip/m 0.63 0.53 0.15 0.1034
下载: 导出CSV
表 3 基于集成模拟平衡位形和快离子分布的波纹损失全要素计算结果
Table 3. Ripple loss results of full calculation based on integrated modeling equilibrium and beam ion distribution.
Trapped fraction/% Prompt loss/% Non-prompt loss/% Total loss/% Co-perp 39 3.3 33.7 37 Co-tang 33 0.8 32.2 34
下载: 导出CSV
表 4 EXL-50U中固定 Ip = 500 kA, 不同Rmax时波纹损失计算结果
Table 4. Ripple loss results of different Rmax of LCFS equilibrium with Ip = 500 kA in EXL-50U.
Trapped fraction/% Total loss/% Rmax =1.323 m 53.7 30.5 Rmax =1.298 m 52.5 28.4 Rmax =1.163 m 45.8 20.8
下载: 导出CSV
表 5 不同NBI角度下的快离子分布中的捕获粒子份额
Table 5. Trapped particle faction of beam ions with different NBI geometry.
Trapped fraction Zelev/m 0 0.2 0.4 0.6 Rtang = 0.407 m 0.37 0.385 0.39 0.39 Rtang = 0.607 m 0.30 0.30 0.295 0.305 Rtang = 0.807 m 0.255 0.245 0.245 0.25 Rtang = 1.007 m 0.295 0.285 0.27 0.27
下载: 导出CSV
表 6 平衡位形LCFS Rmax ～1.16 m, Ip = 500 kA时不同NBI角度和束能Enb下的快离子损失份额
Table 6. Loss faction of NBI fast ions with different NBI geometry and beam energy in LCFS Rmax～1.16 m, Ip = 500 kA equilibrium.
Total loss Enb/keV 20 25 30 35 40 45 50 R = 0.428 m 0.1988 0.2157 0.2319 0.2433 0.2588 0.2687 0.2766 R = 0.607 m 0.125 0.1286 0.1343 0.1432 0.1455 0.15 0.1547 R = 0.807 m 0.1148 0.1179 0.1197 0.1214 0.125 0.1293 0.127
下载: 导出CSV
表 7 不同Ip下的NBI快离子损失粒子份额
Table 7. Trapped particle faction of NBI fast ions with different Ip.
Plasma current Ip/kA Trapped fraction/% Prompt loss/% Total loss/% 500 46.5 4.2 20 600 38.2 3.6 12.4 700 38.6 1.9 9.4 800 39 1.09 7.8 1000 43.4 0.43 7.7
下载: 导出CSV
-
[1] Chen J L, Jian X, Chan V S, Li Z Y, Deng Z, Li G Q, Guo W F, Shi N, Chen X, CFETR Physics Team 2017 Plasma Phys. Control. Fusion 59 075005
Google Scholar
[2] Gorelenkov N N, Pinches S D, Toi K 2014 Nucl. Fusion 54 125001
Google Scholar
[3] 郝保龙, 陈伟, 蔡辉山, 李国强, 王丰, 吴斌, 王进芳, 陈佳乐, 王兆亮, 高翔, Chan Vincent, CFETR TEAM 2020 中国科学:物理学 力学 天文学 50 065201
Google Scholar
Hao B L, Chen W, Cai H S, Li G Q, Wang F, Wu B, Wang J F, Chen J L, Wang Z L, Gao X, Chan V, CFETR TEAM 2020 Sci. Sin. -Phys. Mech. Astron. 50 065201
Google Scholar
[4] Wu B, Hao B L, White R B, Wang J F, Zang Q, Han X F, Hu C D 2017 Plasma Phys. Control. Fusion 59 025004
Google Scholar
[5] Podesta M, Gorelenkova M, Gorelenkov N N, White R B 2017 Plasma Phys. Control. Fusion 59 095008
Google Scholar
[6] Taimourzadeh S, Bass E M, Chen Y, Collins C, Gorelenkov N N, Könies A, Lu Z X, Spong D A, Todo Y, Austin M E, Bao J, Biancalani A, Borchardt M, Bottino A, Heidbrink W W, Kleiber R, Lin Z, Mishchenko A, Shi L, Varela J, Waltz R E, Yu G, Zhang W L, Zhu Y 2019 Nucl. Fusion 59 066006
Google Scholar
[7] Duarte V N, Lestz J B, Gorelenkov N N, White R B 2023 Phys. Rev. Lett. 130 105101
Google Scholar
[8] Pankin A, McCune D, Andre R, Bateman G, Kritz A 2004 Comput. Phys. Commun. 159 157
Google Scholar
[9] White R B, Rutherford P H, Colestock P, Bussac M N 1988 Phys. Rev. Lett. 60 2038
Google Scholar
[10] White R B 2014 The Theory of Toroidally Confined Plasmas (3rd Ed.) (Singapore: World Scientific Publishing Company
[11] White R B, Boozer A H, Hay R 1982 Phys. Fluids 25 575
Google Scholar
[12] Redi M H, White R B, Batha S H, Levinton F M, McCune D C 1997 Phys. Plasmas 4 4001
Google Scholar
[13] Redi M H, Zarnstorff M C, White R B, Budny R V, Janos A C, Owens D K, Schivell J F, Scott S D, Zweben S J 1995 Nucl. Fusion 35 1191
Google Scholar
[14] Redi M H, Budny R V, McCune D C, Miller C O, White R B 1996 Phys. Plasmas 3 3037
Google Scholar
[15] 郝保龙, 陈伟, 李国强, 王晓静, 王兆亮, 吴斌, 臧庆, 揭银先, 林晓东, 高翔, CFETR Team 2021 70 115201
Google Scholar
Hao B L, Chen W, Li G Q, Wang X J, Wang Z L, Wu B, Zang Q, Jie Y X, Lin X D, Gao X, CFETR Team 2021 Acta Phys. Sin. 70 115201
Google Scholar
[16] Wesson J Tokamaks 2011 (New York: Oxford University Press
[17] Hao B L, White R B, Gao X, Li G Q, Chen W, Wang X J, Wu B, Wu M Q, Zhu X, Lin X D, Jie Y X, Zang Q, Li J G, Wan Y X, CFETR Physics Team 2021 Nucl. Fusion 61 046035
Google Scholar
[18] Boozer A H, Kuo-Petravic G, 1981 Phys. Fluids 24 851
Google Scholar
[19] Kramer G J, McLean A, Brooks N, Budny R V, Chen X, Heidbrink W W, Kurki-Suonio T, Nazikian R, Koskela T, Schaffer M J, Shinohara K, Snipes J A, Van Zeeland M A 2013 Nucl. Fusion 53 123018
Google Scholar
[20] ITER Physics Expert Group on Energetic Particles, Heating and Current Drive and ITER Physics Basis Editors 1999 Nucl. Fusion 39 2495
Google Scholar
[21] Tobita K, Nakayama T, Konovalov S V, Sato M 2003 Plasma Phys. Control. Fusion 45 133
Google Scholar
[22] Pinches S D, Chapman I T, Lauber P W, Oliver H J C, Sharapov S E, Shinohara K, Tani K 2015 Phys. Plasmas 22 021807
Google Scholar
下载:
计量
- 文章访问数: 2225
- PDF下载量: 59
- 被引次数: 0
