-
重粒子碰撞中的电子转移涉及复杂的电子关联机制, 极大地影响等离子体中电荷态平衡, 也是X射线的辐射的重要来源之一. 电子转移截面与速率系数是国防工业发展核聚变等离子体所需要的重要原子参数. 基于全量子的非辐射分子轨道密耦合方法, 系统研究了质子碰撞硼原子在
${10}^{-3}—{10}^{3}\;{\rm{e}}{\rm{V}}/{\rm{u}}$ 能量区间内的硼原子电子转移过程. 计算采用多参考组态方法得到总共15个电子转移、激发以及弹性散射的通道, 每个通道对应的分子态能量得到了与实验符合较好的结果. 分子态的绝热势能曲线间的避免交叉现象明显, 构成了电子转移的主要途径. 计算发现, 质子碰撞硼原子过程中2s轨道的电子转移是占主导地位, 2p轨道的电子转移贡献较小. 在低能区, 电子转移截面出现了明显的量子共振现象, 这些共振主要来源于不同能量通道的耦合. 此外, 还计算了不同温度下的质子碰撞硼原子的电子转移速率, 该速率可为复杂等离子体环境的模拟诊断提供重要的原子参数支持.Electron transfer in heavy particle collisions, involving complicated electron correlation mechanisms, greatly affects the charge state balance in plasma, and is also one of important sources for X-ray radiation. Electron transfer cross section and rate coefficient are important atomic parameters required for the development of nuclear fusion plasma in the national defense industry. We systematically investigate the electron transfer process of proton impacting boron atom in an energy range of${10}^{-3}-{10}^{3}\;{\rm{e}}{\rm{V}}/{\rm{u}}$ based on a fully quantum non-radiative molecular orbital close-coupling method. A total of 15 channels of electron transfer, excitation, and elastic scattering are obtained by using the multi-reference configuration interaction method, and the corresponding molecular energy of each channel is in good agreement with the experimental results. The phenomenon of avoiding crossing between the adiabatic potential energy curves of molecular states is obvious, which constituents the main pathway of electron transfer. The calculation shows that the electron transfer of the 2s orbital is dominated in the process of proton impacting boron atom, while the electron transfer of the 2p orbital contributes a little. In the low energy region, there are obvious quantum resonances in the electron transfer cross section, which originate from the coupling between high energy channel and low energy channel. In addition, we calculate the electron transfer rates of proton-impact boron atom at different temperatures, which can provide important atomic parameter which support for simulating and diagnosing complex plasma environments.-
Keywords:
- electron transfer /
- heavy ion collision /
- potential curve
[1] Janev R K, Presnyakov L P, Shevelko V P 1985 Physics of Highly Charged Ions (Berlin-Heidelberg: Springer) pp1–6
[2] Loarte A, Lipschultz B, Kukushkin A S 2007 Nucl. Fusion 47 S203
Google Scholar
[3] Kallman T R, Palmeri P 2007 Rev. Mod. Phys. 79 79
Google Scholar
[4] 刘春华 2009 博士学位论文 (北京: 中国科学院大学)
Liu C H 2009 Ph. D. Dissertation (Beijing: University of the Chinese Academy of Sciences) (in Chinese)
[5] 林晓贺 2019 博士学位论文 (北京: 北京理工大学)
Lin X H 2019 Ph. D. Dissertation (Beijing: Beijing Institute of Technology) (in Chinese)
[6] Liu L, Liu C H, Wang J G, Janev R K 2011 Phys. Rev. A 84 032710
Google Scholar
[7] Gao J W, Wu Y, Sisourat N, Wang J G, Dubois A 2017 Phys. Rev. A 96 052703
Google Scholar
[8] Gao J W, Wu Y, Wang J G, Sisourat N, Dubois A 2018 Phys. Rev. A 97 052709
Google Scholar
[9] Zhang Y W, Gao J G, Wu Y, Zhou F Y, Wang J G, Sisourat N, Dubois A 2020 Phys. Rev. A 102 022814
Google Scholar
[10] Liu C H, Wang J G, Janev R K 2012 Phys. Rev. A 85 042719
Google Scholar
[11] Yan L L, Wu Y, Qu Y Z, Wang J G, Buenker R J 2013 Phys. Rev. A 88 022706
Google Scholar
[12] Liu C H, Liu L, Wang J G 2014 Phys. Rev. A 90 012708
Google Scholar
[13] Liu C H, Wang J G 2013 Phys. Rev. A 87 042709
Google Scholar
[14] Liu C H, Wang J G, Janev R K 2014 Phys. Rev. A 89 062719
Google Scholar
[15] Bruhns H, Kreckel H, Savin D W, seely D G, Havener C C 2008 Phys. Rev. A 77 064702
Google Scholar
[16] Kim H J, Phaneuf R A, Meyer F W, Stelson P H 1987 Phys. Rev. A 17 854
[17] Gieler M, Ziegelwanger P, Aumayr F, Winter H, Fritsch W 1991 J. Phys. B 24 647
Google Scholar
[18] Ebel F, Salzborn E 1987 J. Phys. B 20 4531
Google Scholar
[19] Hayakawa S, Kadomura K, Kimura M, Dutta C M 2004 Phys. Rev. A 70 022708
Google Scholar
[20] Hayakawa H, Helm H, Briggs J S, Salzborn E 2007 Phys. Rev. Lett 99 173202
Google Scholar
[21] Kim H K, Schoffler M S, Houamer S, Chuluunbaatar O, Titze J N, Schmidt L P H, Jahnke T, Schmidt-Bocking H, Galstyan A, Popov Y V, Dorner R 2012 Phys. Rev. A 85 022707
Google Scholar
[22] Bayfield J E, Khayrallah G A 1975 Phys. Rev. A 11 920
Google Scholar
[23] Buenker R J, Liebermann H P, Whitten J L 2001 Chem. Phys. 265 1
Google Scholar
[24] Buenker R J, Liebermann H P, Izgorodina E I 2003 Chem. Phys. 291 115
Google Scholar
[25] Alcheev P G, Buenker R J, Chernov V, Zon B A 2003 J. Mol. Spectrosc. 218 190
Google Scholar
-
图 1 (a) BH+分子
$ {\Sigma } $ 态势能曲线; (b) BH+分子$ {\Pi } $ 态势能曲线Fig. 1. (a) Energy curve of BH+ molecule with
$ \Sigma $ states; (b) energy curve of BH+ molecule with$ {\Pi } $ states.
图 2 质子碰撞B原子过程中2p轨道电子转移截面
Fig. 2. Electron transfer cross section of 2p orbitals in the process of protons colliding with B atom.
图 3 质子碰撞B原子过程中2s和2p轨道电子转移截面
Fig. 3. Electron transfer cross section of 2s and 2p orbitals in the process of protons colliding with B atom.
图 4 径向耦合矩阵元随核间距的变化
Fig. 4. Radial coupling matrix element changes with the nuclear distance.
图 5 转动耦合矩阵元随核间距的变化
Fig. 5. Rotation coupling matrix element varies with the nuclear distance.
表 1 不同分子态对应的解离极限下的原子态以及态能量的理论结果和实验结果
Table 1. Atomic states corresponding to different molecular states under dissociation limit, and the theoretical and experimental results of state energy.
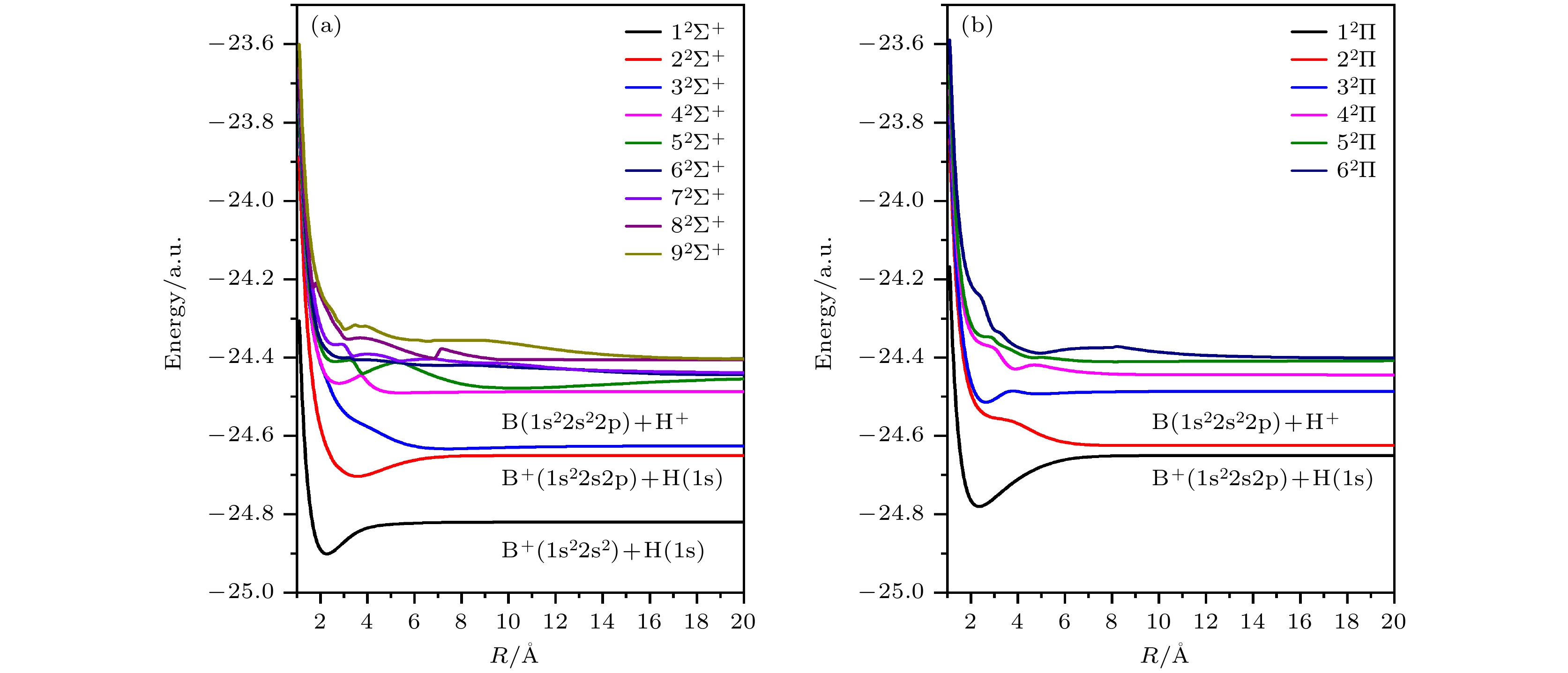
原子态 分子态 能量/eV 理论 实验 误差 $ {{\rm{B}}}^{+}\left(1{{\rm{s}}}^{2}2{{\rm{s}}}^{2}\right)+{\rm{H}}\left(1{\rm{s}}\right) $ $ 1{}_{}{}^{2}{{{\Sigma }}}^{+} $ 0 0 0 $ {{\rm{B}}}^{+}\left(1{{\rm{s}}}^{2}2{{\rm{s}}}^{}2{\rm{p}}\right)+{\rm{H}}\left(1{\rm{s}}\right) $ $ 2{}_{}{}^{2}{{{\Sigma }}}^{+}1{}_{}{}^{2}{{\Pi }} $ 4.6226 4.6230 0.0004 $ {{\rm{B}}}^{}\left(1{{\rm{s}}}^{2}2{{\rm{s}}}^{2}2{\rm{p}}\right)+{{\rm{H}}}^{+} $ $ 3{}_{}{}^{2}{{{\Sigma }}}^{+}2{}_{}{}^{2}{{\Pi }} $ 5.3042 5.3003 0.0039 $ {{\rm{B}}}^{+}\left(1{{\rm{s}}}^{2}2{{\rm{s}}}^{}2{\rm{p}}\right)+{\rm{H}}\left(1{\rm{s}}\right) $ $ 4{}_{}{}^{2}{{{\Sigma }}}^{+}3{}_{}{}^{2}{{\Pi }} $ 9.0663 9.1001 0.0338 $ {{\rm{B}}}^{+}\left(1{{\rm{s}}}^{2}2{{\rm{s}}}^{2}\right)+{\rm{H}}\left(2{\rm{p}}\right) $ $ 5{}_{}{}^{2}{{{\Sigma }}}^{+}4{}_{}{}^{2}{{\Pi }} $ 10.1769 10.1987 0.0218 $ {{\rm{B}}}^{+}\left(1{{\rm{s}}}^{2}2{{\rm{s}}}^{2}\right)+{\rm{H}}\left(2{\rm{s}}\right) $ $ 6{}_{}{}^{2}{{{\Sigma }}}^{+} $ 10.1929 10.1987 0.0058 $ {{\rm{B}}}^{}\left(1{{\rm{s}}}^{2}2{{\rm{s}}}^{2}3{\rm{s}}\right)+{{\rm{H}}}^{+} $ $ 7{}_{}{}^{2}{{{\Sigma }}}^{+} $ 10.2615 10.2597 0.0018 $ {{\rm{B}}}^{}\left(1{{\rm{s}}}^{2}2{\rm{s}}2{{\rm{p}}}^{2}\right)+{{\rm{H}}}^{+} $ $ 8{}_{}{}^{2}{{{\Sigma }}}^{+}5{}_{}{}^{2}{{\Pi }} $ 11.2491 11.2337 0.0154 $ {{\rm{B}}}^{}\left(1{{\rm{s}}}^{2}2{{\rm{s}}}^{2}3{\rm{s}}\right)+{{\rm{H}}}^{+} $ $ 9{}_{}{}^{2}{{{\Sigma }}}^{+}6{}_{}{}^{2}{{\Pi }} $ 11.3623 11.3273 0.0350 
下载: 导出CSV
表 2 电子转移总的速率系数, 其中包含2s和2p轨道的电子转移
Table 2. Total rate coefficient of electron transfer, including electron transfer of 2s and 2p orbitals.
$ T/{\rm{K}} $ $ 2 $ $ 5 $ $ 10 $ $ 40 $ $\alpha /\left({10}^{-12}~{ {\rm{c} }{\rm{m} } }^{3}{\cdot{\rm{s} } }^{-1}\right)$ $ 1.72\times {10}^{-8} $ $ 5.09\times {10}^{-4} $ $ 1.40\times {10}^{-2} $ $ 1.24\times {10}^{-1} $ $ T/{\rm{K}} $ $ 100 $ $ 500 $ $ 1000 $ $ 6000 $ $\alpha /\left({10}^{-14}~{ {\rm{c} }{\rm{m} } }^{3}{\cdot{\rm{s} } }^{-1}\right)$ $ 14.7 $ $ 10.3 $ $ 8.62 $ $ 46.9 $ $T/{(10}^{5}~{\rm{K} })$ $ 0.1 $ $ 0.5 $ $ 1.0 $ $ 5.0 $ $\alpha /\left({10}^{-12}~{ {\rm{c} }{\rm{m} } }^{3}{\cdot{\rm{s} } }^{-1}\right)$ $ 1.72 $ $ 8.91\times {10}^{1} $ $ 3.86\times {10}^{2} $ $ 4.74\times {10}^{3} $ $T/{(10}^{6}~{\rm{K} })$ $ 1.0 $ $ 5.0 $ $ 10 $ $ 50 $ $\alpha /\left({10}^{-9}~{ {\rm{c} }{\rm{m} } }^{3}{\cdot{\rm{s} } }^{-1}\right)$ $ 9.38 $ $ 25.8 $ $ 26.8 $ $ 7.19 $
下载: 导出CSV
-
[1] Janev R K, Presnyakov L P, Shevelko V P 1985 Physics of Highly Charged Ions (Berlin-Heidelberg: Springer) pp1–6
[2] Loarte A, Lipschultz B, Kukushkin A S 2007 Nucl. Fusion 47 S203
Google Scholar
[3] Kallman T R, Palmeri P 2007 Rev. Mod. Phys. 79 79
Google Scholar
[4] 刘春华 2009 博士学位论文 (北京: 中国科学院大学)
Liu C H 2009 Ph. D. Dissertation (Beijing: University of the Chinese Academy of Sciences) (in Chinese)
[5] 林晓贺 2019 博士学位论文 (北京: 北京理工大学)
Lin X H 2019 Ph. D. Dissertation (Beijing: Beijing Institute of Technology) (in Chinese)
[6] Liu L, Liu C H, Wang J G, Janev R K 2011 Phys. Rev. A 84 032710
Google Scholar
[7] Gao J W, Wu Y, Sisourat N, Wang J G, Dubois A 2017 Phys. Rev. A 96 052703
Google Scholar
[8] Gao J W, Wu Y, Wang J G, Sisourat N, Dubois A 2018 Phys. Rev. A 97 052709
Google Scholar
[9] Zhang Y W, Gao J G, Wu Y, Zhou F Y, Wang J G, Sisourat N, Dubois A 2020 Phys. Rev. A 102 022814
Google Scholar
[10] Liu C H, Wang J G, Janev R K 2012 Phys. Rev. A 85 042719
Google Scholar
[11] Yan L L, Wu Y, Qu Y Z, Wang J G, Buenker R J 2013 Phys. Rev. A 88 022706
Google Scholar
[12] Liu C H, Liu L, Wang J G 2014 Phys. Rev. A 90 012708
Google Scholar
[13] Liu C H, Wang J G 2013 Phys. Rev. A 87 042709
Google Scholar
[14] Liu C H, Wang J G, Janev R K 2014 Phys. Rev. A 89 062719
Google Scholar
[15] Bruhns H, Kreckel H, Savin D W, seely D G, Havener C C 2008 Phys. Rev. A 77 064702
Google Scholar
[16] Kim H J, Phaneuf R A, Meyer F W, Stelson P H 1987 Phys. Rev. A 17 854
[17] Gieler M, Ziegelwanger P, Aumayr F, Winter H, Fritsch W 1991 J. Phys. B 24 647
Google Scholar
[18] Ebel F, Salzborn E 1987 J. Phys. B 20 4531
Google Scholar
[19] Hayakawa S, Kadomura K, Kimura M, Dutta C M 2004 Phys. Rev. A 70 022708
Google Scholar
[20] Hayakawa H, Helm H, Briggs J S, Salzborn E 2007 Phys. Rev. Lett 99 173202
Google Scholar
[21] Kim H K, Schoffler M S, Houamer S, Chuluunbaatar O, Titze J N, Schmidt L P H, Jahnke T, Schmidt-Bocking H, Galstyan A, Popov Y V, Dorner R 2012 Phys. Rev. A 85 022707
Google Scholar
[22] Bayfield J E, Khayrallah G A 1975 Phys. Rev. A 11 920
Google Scholar
[23] Buenker R J, Liebermann H P, Whitten J L 2001 Chem. Phys. 265 1
Google Scholar
[24] Buenker R J, Liebermann H P, Izgorodina E I 2003 Chem. Phys. 291 115
Google Scholar
[25] Alcheev P G, Buenker R J, Chernov V, Zon B A 2003 J. Mol. Spectrosc. 218 190
Google Scholar
下载:
计量
- 文章访问数: 2961
- PDF下载量: 73
- 被引次数: 0
