-
以磁隧道结/重金属层组成的三端口磁隧道结为理论模型, 通过对包含自旋转移矩和自旋轨道矩的Landau-Lifshitz-Gilbert (LLG)方程做线性化稳定性分析, 研究了自旋轨道矩协助自旋转移矩驱动的磁化强度翻转. 发现在自旋轨道矩协助下, 磁矩的翻转时间极大减小, 翻转时间随自旋轨道矩电流密度的增大而减小, 且自旋转移矩和自旋轨道矩的结合可实现零磁场的磁化翻转. 另外, 相比自旋轨道矩的类阻尼项, 类场项在磁化强度的翻转中起着主导作用, 且自旋轨道矩类场项的出现也可以减小磁化强度的翻转时间, 磁化强度翻转时间随自旋轨道矩类场项强度的增大而减小.As the data writing scheme of magnetization reversal driven by spin-transfer torque can overcome the shortcomings of traditional magnetic-field writing mechanism, it has become a mainstream way of implementing information writing in magnetic random access memory. However, the explosive growth of information shows higher requirements for data storage and information processing, thus magnetic random access memories based on spin-transfer torque data writing method pose several issues, including barrier reliability and limited storage speed. Recent experimental studies have shown that the spin-orbit torque through the spin Hall effect or Rashba effect in heavy-metal/ferromagnetic bilayer structures has the potential advantages in overcoming these limitations. They can also be used to drive magnetization to achieve rapid reversal. Especially, the three-terminal magnetic tunnel junction separates data reading from writing current. It has the advantages of faster writing speed and better stability and thus becomes the most promising magnetic storage technique at present. The magnetization reversal driven by spin-orbit-assisted spin-transfer torque in a three-terminal magnetic tunnel junction is studied theoretically in this work. By linearizing the Landau-Lifshitz-Gilbert equation with the additional spin-transfer torque term and spin-orbit torque term in the spherical coordinates, two coupled differential equations and the new equilibrium directions are obtained. With the stability analysis of the new equilibrium directions, the phase diagrams defined in parameter space spanned by the current densities of spin-transfer and spin-orbit torques are established. There are several magnetic states in the phase diagrams, including quasi-parallel stable states, quasi-antiparallel stable states, and bistable states. By adjusting the current density of the spin-transfer torque, the magnetization reversal between two stable states is realized. It is found that the magnetization reversal time is greatly reduced with the assisting of spin-orbit torque, and it decreases with the augment of current density of spin-orbit torque. Meanwhile, the zero-field magnetization reversal can be realized through the interplay between spin-orbit torque and spin-transfer torque. In addition, compared with the damping-like term of spin-orbit torque, the field-like one plays a leading role in magnetization reversal. The presence of field-like term of spin-orbit torque can also reduce the reversal time that decreases with the increase of the ratio of field-like torque to damping-like one.
-
Keywords:
- magnetization reversal /
- spin-transfer torque /
- spin-orbit torque
[1] Slonczewski J C 1996 J. Magn. Magn. Mater. 159 L1
Google Scholar
[2] Berger L 1996 Phys. Rev. B 54 9353
Google Scholar
[3] Katine J A, Albert F J, Buhrman R A, Myers E B, Ralph D C 2000 Phys. Rev. Lett. 84 3149
Google Scholar
[4] Yuasa S, Hono K, Hu G, Worledge D C 2018 MRS. Bull. 43 352
Google Scholar
[5] 赵巍胜, 王昭昊, 彭守仲, 王乐知, 常亮, 张有光 2016 中国科学: 物理学 力学 天文学 46 107306
Zhao W S, Wang Z H, Peng S Z, Wang L Z, Chang L, Zhang Y G 2016 Sci. Sin.: Physics, Mechanics & Astronomy 46 107306
[6] Sato N, Xue F, White R M, Bi C, Wang S X 2018 Nat. Electron. 1 508
Google Scholar
[7] Cubukcu M, Boulle O, Mikuszeit N, Hamelin C, Brächer T, Lamard N, Cyrille M C, Buda-Prejbeanu L, Garello K, Miron I M, Klein O, de Loubens G, Naletov V V, Langer J, Ocker B, Pietro, Gaudin G 2018 IEEE Trans. Magn. 54 9300204
Google Scholar
[8] Taniguchi T 2019 J. Magn. Magn. Mater. 483 281
Google Scholar
[9] Liu L Q, Moriyama T, Ralph D C, Buhrman R A 2011 Phys. Rev. Lett. 106 036601
Google Scholar
[10] Pai C F, Liu L Q, Li Y, Tseng H W, Ralph D C, Buhrman R A 2012 Appl. Phys. Lett. 101 122404
Google Scholar
[11] Liu L Q, Lee O J, Gudmundsen T J, Ralph D C, Buhrman R A 2012 Phys. Rev. Lett. 109 096602
Google Scholar
[12] Liu L Q, Pai C F, Li Y, Tseng H W, Ralph D C, Buhrman R A 2012 Science 336 555
Google Scholar
[13] Liu L Q, Pai C F, Ralph D C, Buhrman R A 2012 Phys. Rev. Lett. 109 186602
Google Scholar
[14] Cai K M, Meiyin Yang M Y, Ju H L, Wang S M, Ji Y, Li B H, Edmonds K W, Sheng Y, Zhang B, Zhang N, Liu S, Zheng H Z, Wang K Y 2017 Nat. Mater. 16 712
Google Scholar
[15] Wang X, Wan C H, Kong W J, Zhang X, Xing Y W, Fang C, Tao B S, Yang W L, Huang L, Wu H, Irfan M, Han X F 2018 Adv. Mater. 30 1801318
Google Scholar
[16] Kwak W Y, Kwon J H, Grünberg P, Han S H, Cho B K 2018 Sci. Rep. 8 382
Google Scholar
[17] Zhao X Z, Zhang X Y, Yang H W, Cai W L, Zhao Y L, Wang Z H, Zhao W S 2019 Nanotechnology 30 335707
Google Scholar
[18] Liu L, Zhou C H, Shu X Y, Li C J, Zhao T Y, Lin W N, Deng J Y, Xie Q D, Chen S H, Zhou J, Guo R, Wang H, Yu J H, Shi S, Yang P, Stenphen P, Aurelien M, Chen J S 2021 Nat. Nanotechnol. 16 277
Google Scholar
[19] Sheng Y, Kevin W E, Ma X Q, Zheng H Z, Wang K Y 2018 Adv. Electron. Mater. 4 1800224
Google Scholar
[20] Cao Y, Sheng Y, Kevin W E, Ji Yang, Zheng H Z, Wang K Y 2020 Adv. Mater. 32 1907929
Google Scholar
[21] Wang M X, Cai W L, Zhu D Q, Wang Z H, Kan J M, Zhao Z Y, Cao K H, Wang Z L, Zhang Y G, Zhang T R, Park C D, Wang J P, Alert F, Zhao W S 2018 Nat. Electron. 1 582
Google Scholar
[22] Fukami S, Anekawa T, Zhang C, Ohno H 2016 Nat. Nanotechnol. 11 621
Google Scholar
[23] Isogami S, Shiokawa Y, Tsumita A, Komura E, Ishitani Y, Hamanaka K, Taniguchi T, Mitani S, Sasaki T, Hayashi M 2021 Sci. Rep. 11 16676
Google Scholar
[24] Zhang C L, Takeuchi Y, Shunsuke Fukami S, Ohno H 2021 Appl. Phys. Lett. 118 092406
Google Scholar
[25] Garello K, Miron I M, Avci C O, Freimuth F, Mokrousov Y, Blügel S, Auffret S, Boulle O, Gaudin G, Gambardella P 2013 Nat. Nanotechnol. 8 587
Google Scholar
[26] Kurebayashi H, Sinaova J, Fang D, lrvine A C, Skinner T D, Wunderlich J, Novák V, Canpion R P, Gallagher B L, Vehstedt E K, Zârba L P, Výborný K, Ferguson A J, Jungwirth T 2014 Nat. Nanotechnol. 9 211
Google Scholar
[27] Ou Y X, Pai C F, Shi S J, Ralph D C, Buhrman R A 2016 Phys. Rev. B 94 140414
Google Scholar
[28] Fan X, Celik H, Wu J, Ni C Y, Lee K J, Lorenz V O, Xiao J Q 2014 Nat. Commun. 5 3042
Google Scholar
[29] Lee J M, Kwon J H, Ramaswamy R, Yoon J, Son J, Qiu X, Mishra R, Srivastava S, Cai K, Yang H 2018 Commun. Phys. 1 2
Google Scholar
[30] Zhuo Y D, Cai W L, Zhu D Q, Zhang H C, Du A, Cao K H, Yin J L, Huang Y, Shi K W, Zhao W S 2022 Sci. Sin.: Physics, Mechanics & Astronomy 65 107511
[31] Mangin S, Ravelosona D, Katine J A, Carey M J, Terris B D, Fullerton E E 2006 Nat. Mater. 5 210
Google Scholar
[32] 王日兴, 叶华, 王丽娟, 敖章洪 2017 66 127201
Google Scholar
Wang R X, Ye H, Wang L J, Ao Z H 2017 Acta Phys. Sin. 66 127201
Google Scholar
-
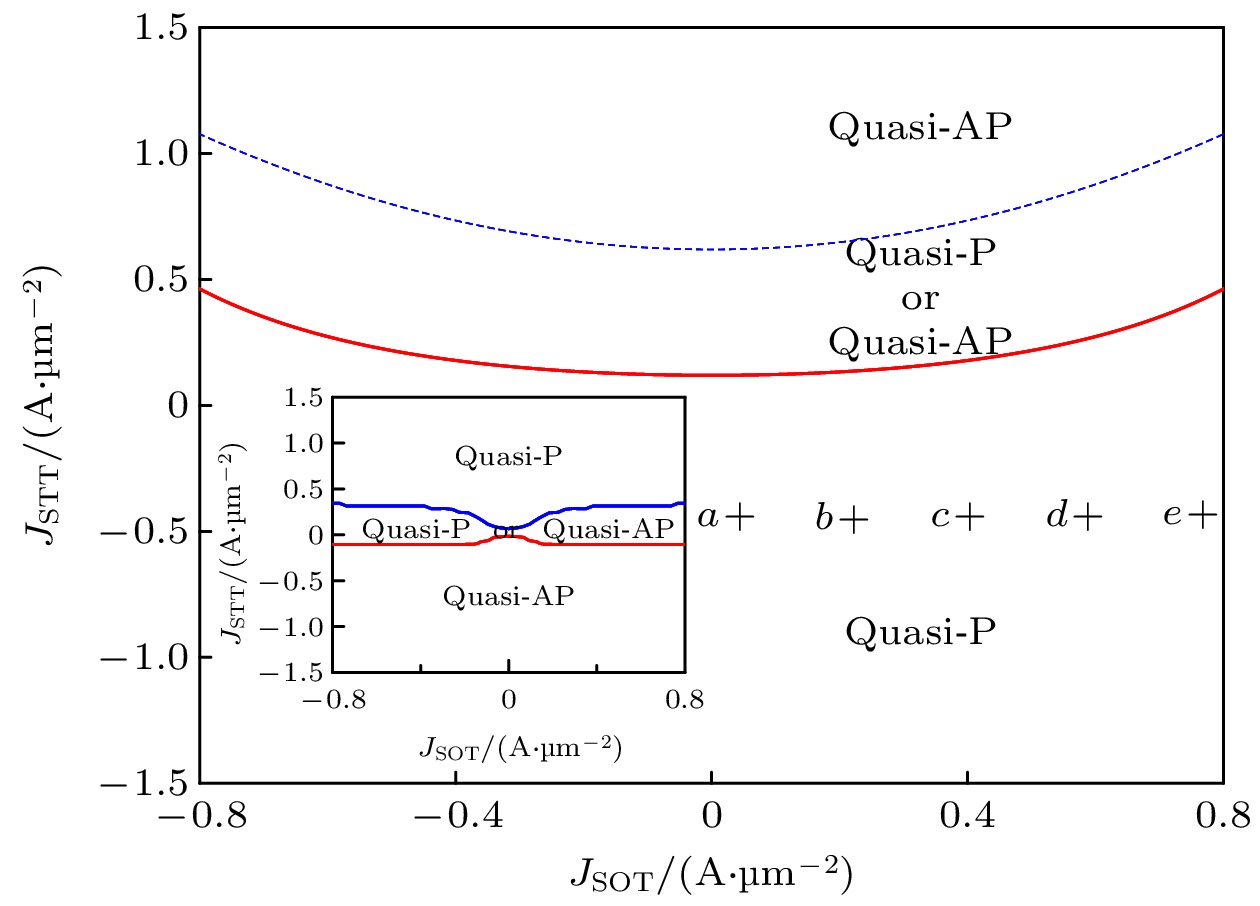
图 2 以自旋转移矩电流密度
$ J_{{\rm{STT}}} $ 和自旋轨道矩电流密度$ J_{{\rm{SOT}}} $ 为控制参数的相图(外磁场$ h_{0} = 2 $ ), 插图为$ h_{0} = 0 $ 时的磁性状态相图Fig. 2. Phase diagram defined in parameter space spanned by the current densities of STT and SOT for the external magnetic field
$ h_{0} = 2 $ . The inset is the phase diagram of magnetic states for$ h_{0} = $ $ 0 $ .
图 3 自由层磁化强度分量
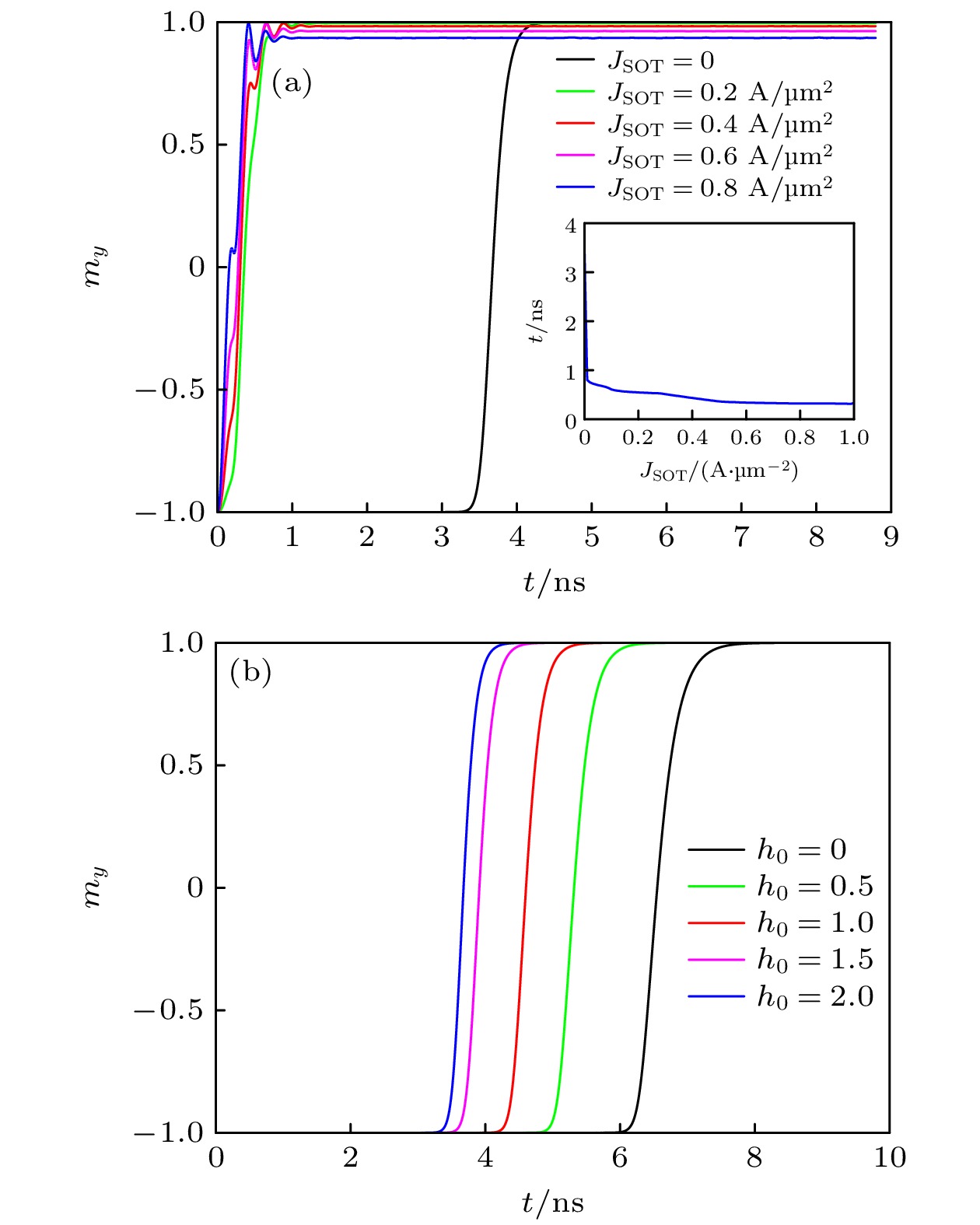
$m_y $ 随时间的演化轨迹 (a) 图2中“a”, “b”, “c”, “d”和“e”五点的自由层磁化强度分量$ m_{y} $ 随时间的演化轨迹, 插图为翻转时间随自旋轨道矩电流密度的变化关系; (b) 图2中“a”点对应的不同外磁场作用下$ m_{y} $ 随时间的演化轨迹Fig. 3. Time evolutions of free-layer magnetization
$ m_{y} $ : (a) Time evolutions of free -layer magnetization$m_y $ for five points “a”, “b”, “c” “d”, and “e” in Fig. 2，the inset shows the dependence of the reversal time on the SOT current density; (b) time evolutions of$ m_{y} $ for point “a” in Fig. 2 with different external magnetic fields
图 4 以自旋转移矩电流密度
$ J_{{\rm{STT}}} $ 和自旋轨道矩类场项和类阻尼项之比β为控制参数的相图Fig. 4. Phase diagram defined in parameter space controlled by the current density of STT and the ratio of field-like term to damping-like one of SOT.
-
[1] Slonczewski J C 1996 J. Magn. Magn. Mater. 159 L1
Google Scholar
[2] Berger L 1996 Phys. Rev. B 54 9353
Google Scholar
[3] Katine J A, Albert F J, Buhrman R A, Myers E B, Ralph D C 2000 Phys. Rev. Lett. 84 3149
Google Scholar
[4] Yuasa S, Hono K, Hu G, Worledge D C 2018 MRS. Bull. 43 352
Google Scholar
[5] 赵巍胜, 王昭昊, 彭守仲, 王乐知, 常亮, 张有光 2016 中国科学: 物理学 力学 天文学 46 107306
Zhao W S, Wang Z H, Peng S Z, Wang L Z, Chang L, Zhang Y G 2016 Sci. Sin.: Physics, Mechanics & Astronomy 46 107306
[6] Sato N, Xue F, White R M, Bi C, Wang S X 2018 Nat. Electron. 1 508
Google Scholar
[7] Cubukcu M, Boulle O, Mikuszeit N, Hamelin C, Brächer T, Lamard N, Cyrille M C, Buda-Prejbeanu L, Garello K, Miron I M, Klein O, de Loubens G, Naletov V V, Langer J, Ocker B, Pietro, Gaudin G 2018 IEEE Trans. Magn. 54 9300204
Google Scholar
[8] Taniguchi T 2019 J. Magn. Magn. Mater. 483 281
Google Scholar
[9] Liu L Q, Moriyama T, Ralph D C, Buhrman R A 2011 Phys. Rev. Lett. 106 036601
Google Scholar
[10] Pai C F, Liu L Q, Li Y, Tseng H W, Ralph D C, Buhrman R A 2012 Appl. Phys. Lett. 101 122404
Google Scholar
[11] Liu L Q, Lee O J, Gudmundsen T J, Ralph D C, Buhrman R A 2012 Phys. Rev. Lett. 109 096602
Google Scholar
[12] Liu L Q, Pai C F, Li Y, Tseng H W, Ralph D C, Buhrman R A 2012 Science 336 555
Google Scholar
[13] Liu L Q, Pai C F, Ralph D C, Buhrman R A 2012 Phys. Rev. Lett. 109 186602
Google Scholar
[14] Cai K M, Meiyin Yang M Y, Ju H L, Wang S M, Ji Y, Li B H, Edmonds K W, Sheng Y, Zhang B, Zhang N, Liu S, Zheng H Z, Wang K Y 2017 Nat. Mater. 16 712
Google Scholar
[15] Wang X, Wan C H, Kong W J, Zhang X, Xing Y W, Fang C, Tao B S, Yang W L, Huang L, Wu H, Irfan M, Han X F 2018 Adv. Mater. 30 1801318
Google Scholar
[16] Kwak W Y, Kwon J H, Grünberg P, Han S H, Cho B K 2018 Sci. Rep. 8 382
Google Scholar
[17] Zhao X Z, Zhang X Y, Yang H W, Cai W L, Zhao Y L, Wang Z H, Zhao W S 2019 Nanotechnology 30 335707
Google Scholar
[18] Liu L, Zhou C H, Shu X Y, Li C J, Zhao T Y, Lin W N, Deng J Y, Xie Q D, Chen S H, Zhou J, Guo R, Wang H, Yu J H, Shi S, Yang P, Stenphen P, Aurelien M, Chen J S 2021 Nat. Nanotechnol. 16 277
Google Scholar
[19] Sheng Y, Kevin W E, Ma X Q, Zheng H Z, Wang K Y 2018 Adv. Electron. Mater. 4 1800224
Google Scholar
[20] Cao Y, Sheng Y, Kevin W E, Ji Yang, Zheng H Z, Wang K Y 2020 Adv. Mater. 32 1907929
Google Scholar
[21] Wang M X, Cai W L, Zhu D Q, Wang Z H, Kan J M, Zhao Z Y, Cao K H, Wang Z L, Zhang Y G, Zhang T R, Park C D, Wang J P, Alert F, Zhao W S 2018 Nat. Electron. 1 582
Google Scholar
[22] Fukami S, Anekawa T, Zhang C, Ohno H 2016 Nat. Nanotechnol. 11 621
Google Scholar
[23] Isogami S, Shiokawa Y, Tsumita A, Komura E, Ishitani Y, Hamanaka K, Taniguchi T, Mitani S, Sasaki T, Hayashi M 2021 Sci. Rep. 11 16676
Google Scholar
[24] Zhang C L, Takeuchi Y, Shunsuke Fukami S, Ohno H 2021 Appl. Phys. Lett. 118 092406
Google Scholar
[25] Garello K, Miron I M, Avci C O, Freimuth F, Mokrousov Y, Blügel S, Auffret S, Boulle O, Gaudin G, Gambardella P 2013 Nat. Nanotechnol. 8 587
Google Scholar
[26] Kurebayashi H, Sinaova J, Fang D, lrvine A C, Skinner T D, Wunderlich J, Novák V, Canpion R P, Gallagher B L, Vehstedt E K, Zârba L P, Výborný K, Ferguson A J, Jungwirth T 2014 Nat. Nanotechnol. 9 211
Google Scholar
[27] Ou Y X, Pai C F, Shi S J, Ralph D C, Buhrman R A 2016 Phys. Rev. B 94 140414
Google Scholar
[28] Fan X, Celik H, Wu J, Ni C Y, Lee K J, Lorenz V O, Xiao J Q 2014 Nat. Commun. 5 3042
Google Scholar
[29] Lee J M, Kwon J H, Ramaswamy R, Yoon J, Son J, Qiu X, Mishra R, Srivastava S, Cai K, Yang H 2018 Commun. Phys. 1 2
Google Scholar
[30] Zhuo Y D, Cai W L, Zhu D Q, Zhang H C, Du A, Cao K H, Yin J L, Huang Y, Shi K W, Zhao W S 2022 Sci. Sin.: Physics, Mechanics & Astronomy 65 107511
[31] Mangin S, Ravelosona D, Katine J A, Carey M J, Terris B D, Fullerton E E 2006 Nat. Mater. 5 210
Google Scholar
[32] 王日兴, 叶华, 王丽娟, 敖章洪 2017 66 127201
Google Scholar
Wang R X, Ye H, Wang L J, Ao Z H 2017 Acta Phys. Sin. 66 127201
Google Scholar
下载:
计量
- 文章访问数: 3550
- PDF下载量: 105
- 被引次数: 0
