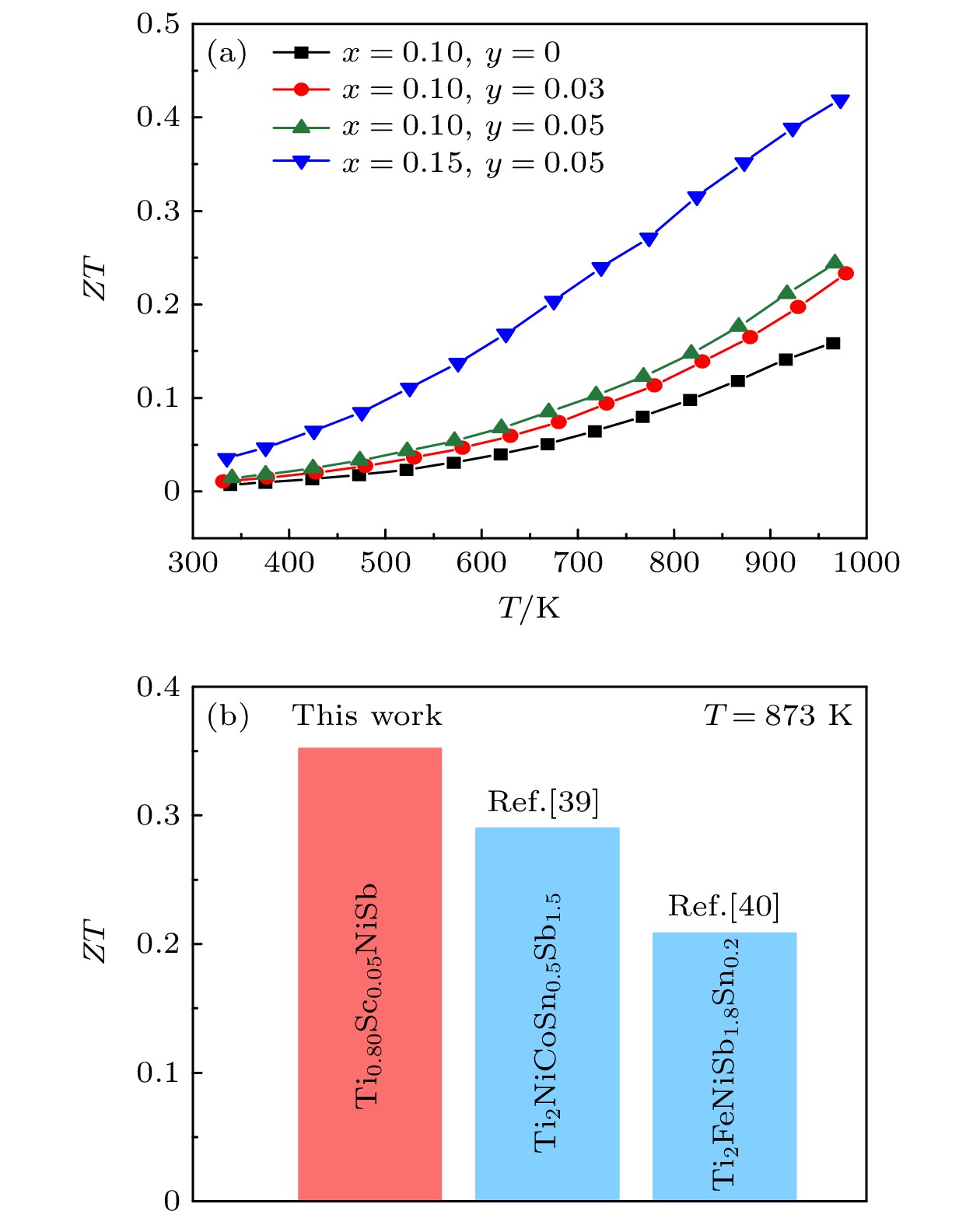
-
采用高能球磨法制备了Ti1–xNiSb (x = 0, 0.10, 0.15, 0.20, 0.25) 和Ti1–x–yScyNiSb (x = 0.10, 0.15; y = 0.03, 0.05) 样品, 并系统地研究了Sc掺杂对Ti1–xNiSb样品的物相、微结构以及电热输运性能的影响. 实验结果表明, Sc掺杂能够有效降低载流子浓度, 提高塞贝克系数, 改善材料的电输运性能. 此外, 由于Sc掺杂能够提高原子间的结合能, 从而有效减少了NiSb杂相. Ti1–x–yScyNiSb的晶格热导率随Sc掺杂而上升, 这可归因于化学键的增强以及电声散射作用的减弱. 但是载流子浓度的急剧下降导致样品的电子热导率显著下降, 从而Ti1–x–yScyNiSb样品的总热导率明显降低. 最终, Ti0.8Sc0.05NiSb样品获得最佳的热电性能, 其功率因子在973 K达到17.7 μW·cm-1·K-2, 无量纲热电优值ZT在973 K达到0.42, 相比未掺杂的单相Ti0.9NiSb样品提升了180%.The nominal composition TiNiSb with 19 valence electrons is demonstrated to be composed of off-stoichiometric half-Heusler phase and impurities. In this work, the Ti1–xNiSb (x = 0, 0.10, 0.15, 0.20, 0.25) samples are prepared by ball milling and spark plasma sintering. The single-phase Ti0.9NiSb sample, deviating from the theoretical composition Ti0.75NiSb base on 18-electron rule, is obtained, which might be ascribed to the small defect formation energy of Ti filling the vacancy as well as our ball-milling preparation method. With the single-phase Ti0.9NiSb sample used as the base material, a small amount of Sc is used to partially replace Ti in order to further reduce the carrier concentration. Thus, the Ti1–x–yScyNiSb (x = 0.10, 0.15; y = 0.03, 0.05) samples are designed to investigate the effect of Sc doping on the thermoelectric properties. The X-ray powder diffraction (XRD) and scanning electron microscopy (SEM) analysis confirm the single-phase nature of the Ti1–x–yScyNiSb samples. Energy-dispersive X-ray spectroscopy (EDS) results indicate that the actual compositions of the Ti1–x–yScyNiSb samples are consistent well with their nominal compositions, and all elements are distributed uniformly in the sample. Moreover, the doping of Sc can increase the content of Ti vacancy while maintaining the single-phase structure, which could be attributed to the higher binding energy between Sc and Sb because the electronegativity of Sc is less than that of Ti. Both the substitution of Sc for Ti and the increase of the Ti vacancies significantly reduce the carrier concentration, which decreases from ~13.6 × 1021 cm–3 for Ti0.9NiSb to ~3.4 × 1021 cm–3 for Ti0.8Sc0.05NiSb. The reduced carrier concentration results in greatly increased Seebeck coefficient, therefore the Ti0.8Sc0.05NiSb sample achieves a power factor as high as 17.7 μW·cm-1·K-2 at 973 K. Although the lattice thermal conductivity of Sc-doped sample increases slightly due to the reduction of electron–phonon scattering and the enhancement of chemical bonds, the total thermal conductivity decreases dramatically due to the electronic thermal conductivity decreasing greatly. Finally, the Ti0.8Sc0.05NiSb sample reaches a ZT value of ~0.42 at 973 K, which is 180% higher than that of Ti0.9NiSb sample. Despite the fact that the thermoelectric performance of our sample is still inferior to those of the state-of-the-art off-stoichiometric 19-electron half-Heusler alloys, this work demonstrates that the thermoelectric performance of Ti1–xNiSb can be further improved by non-isoelectronic doping.
-
Keywords:
- TiNiSb /
- half-Heusler alloy /
- vacancies /
- thermoelectric properties
[1] Bell L E 2008 Science 321 1457
Google Scholar
[2] Jia N, Cao J, Tan X Y, Dong J F, Liu H F, Tan C K I, Xu J W, Yan Q Y, Loh X J, Suwardi A 2021 Energy Environ. Sci. 21 100519
Google Scholar
[3] Min R A, Wang Y X, Jiang X, Chen R C, Kang H J, Guo E Y, Chen Z N, Yang X, Wang T M 2022 Chem. Eng. J. 449 137898
Google Scholar
[4] Joshi G, Dahal T, Chen S, Wang H Z, Shiomi J, Chen G, Ren Z F 2013 Nano Energy 2 82
Google Scholar
[5] Yu C, Zhu T J, Shi R Z, Zhang Y, Zhao X B, He J 2009 Acta Mater. 57 2757
Google Scholar
[6] Fu C G, Zhu T J, Liu Y T, Xie H H, Zhao X B 2015 Energy Environ. Sci. 8 216
Google Scholar
[7] Pei Y Z, Shi X Y, LaLonde A, Wang H, Chen L D, Snyder G J 2011 Nature 473 66
Google Scholar
[8] Fu C G, Zhu T J, Pei Y Z, Xie H H, Wang H, Snyder G J, Liu Y, Liu Y T, Zhao X B 2014 Adv. Energy Mater. 4 1400600
Google Scholar
[9] Tan C, Wang H X, Yao J, Chen T T, Wang L, Sun Y Q, Khan M, Wang H C, Wang C L 2022 J. Eur. Ceram. Soc. 42 7010
Google Scholar
[10] Biswas K, He J Q, Blum I D, Wu C I, Hogan T P, Seidman D N, Dravid V P, Kanatzidis M G 2012 Nature 489 414
Google Scholar
[11] Sun Y J, Shuai Z G, Wang D 2019 J. Phys. Chem. C 123 12001
Google Scholar
[12] He R, Gahlawat S, Guo C F, Chen S, Dahal T, Zhang H, Liu W S, Zhang Q, Chere E, White K, Ren Z F 2015 Phys. Status. Solidi. A 212 2191
Google Scholar
[13] Graf T, Felser C, Parkin S S P 2011 Prog. Solid. State Ch. 39 1
Google Scholar
[14] Sakurada S, Shutoh N 2005 Appl. Phys. Lett. 86 082105
Google Scholar
[15] Uher C, Yang J, Hu S, Morelli D T, Meisner G P 1999 Phys. Rev. B 59 8615
Google Scholar
[16] 王鹏将, 康慧君, 杨雄, 刘颖, 程成, 王同敏 2022 无机材料学报 37 717
Google Scholar
Wang P J, Kang H J, Yang X, Liu Y, Cheng C, Wang T M 2022 J. Inorg. Mater. 37 717
Google Scholar
[17] Sekimoto T, Kurosaki K, Muta H, Yamanaka S 2006 Mater. Trans. 47 1445
Google Scholar
[18] Sekimoto T, Kurosaki K, Muta H, Yamanaka S 2005 Mater. Trans. 46 1481
Google Scholar
[19] Sekimoto T, Kurosaki K, Muta H, Yamanaka S 2007 Jpn. J. Appl. Phys. 46 L673
Google Scholar
[20] Huang Y, Hayashi K, Miyazaki Y 2020 Chem. Mater. 32 5173
Google Scholar
[21] Joshi G, He R, Engber M, Samsonidze G, Pantha T, Dahal E, Dahal K, Yang J, Lan Y C, Kozinsky B, Ren Z F 2014 Energy Environ. Sci. 7 4070
Google Scholar
[22] Zhu H T, Mao J, Li Y W, et al. 2019 Nat. Commun. 10 270
Google Scholar
[23] Xia K, Liu Y, Anand S, Snyder G J, Xin J, Yu J, Zhao X, Zhu T 2018 Adv. Funct. Mater. 28 1705845
Google Scholar
[24] Li S, Bai F X, Wang R F, Chen C, Li X F, Cao F, Yu B, Sui J H, Liu X J, Ren Z F, Zhang Q 2020 Ann. Phys. 532 1900440
Google Scholar
[25] Miranda J, Gruhn T 2022 J. Electron. Mater. 51 2043
Google Scholar
[26] Huang L H, Wang J C, Mo X B, Lei X B, Ma S D, Wang C, Zhang Q Y 2019 Materials 12 1637
Google Scholar
[27] Kainuma R, Umino R, Xu X, Han K, Omori T 2020 J. Phase. Equilibria. Diffus. 41 116
Google Scholar
[28] Romaka V V, Rogl P, Romaka L, Stadnyk Y, Melnychenko N, Grytsiv A, Falmbigl M, Skryabina N 2013 J. Solid State Chem. 197 103
Google Scholar
[29] Anand S, Xia K Y, Zhu T J, Wolverton C, Snyder G J 2018 Adv. Energy Mater. 8 1801409
Google Scholar
[30] Luo F, Wang J, Zhu C, He X, Zhang S, Wang J F, Liu H X, Sun Z G 2022 J. Mater. Chem. A 10 9655
Google Scholar
[31] Anand S, Xia K Y, Hegde V I, Aydemir U, Kocevski V, Zhu T J, Wolverton C, Snyder G J 2018 Energy Environ. Sci. 11 1480
Google Scholar
[32] Romaka V V, Rogl G, Grytsiv A, Rogl P 2020 Comput. Mater. Sci. 172 109307
Google Scholar
[33] Zhou M, Chen L D, Feng C D, Wang D L, Li J F 2007 J. Appl. Phys. 101 113714
Google Scholar
[34] Zhao D G, Wang L, Bo L, Wu D 2018 Metals 8 61
Google Scholar
[35] Tavassoli A, Failamani F, Grytsiv A, Rogl G, Heinrich P, Müller H, Bauer E, Zehetbauer M, Rogl P 2017 Acta Mater. 135 263
Google Scholar
[36] Kim H S, Gibbs Z M, Tang Y L, Wang H, Snyder G J 2015 APL Mater. 3 041506
Google Scholar
[37] 沈家骏, 方腾, 傅铁铮, 忻佳展, 赵新兵, 朱铁军 2019 无机材料学报 34 260
Google Scholar
Shen J J, Fang T, Fu T Z, Xin J Z, Zhao X B, Zhu T J 2019 J. Inorg. Mater. 34 260
Google Scholar
[38] Zhu T J, Yu G T, Xu J, Wu H J, Fu C G, Liu X H, He J Q, Zhao X B 2016 Adv. Electron. Mater. 2 1600171
Google Scholar
[39] Karati A, Hariharan V S, Ghosh S, Prasad A, Nagini M, Guruvidyathri K, Mallik R C, Shabadi R, Bichler L, Murty B S, Varadaraju U V 2020 Scr. Mater. 186 375
Google Scholar
[40] Hasan R, Park T, Kim S I, Kim H S, Jo S, Lee K H 2022 Adv. Energy Sustainability Res. 3 2100206
Google Scholar
[41] Zhang X Y, Bu Z L, Shi X M, Chen Z W, Lin S Q, Shan B, Wood M, Snyder A H, Chen L D, Snyder G J, Pei Y Z 2020 Sci. Adv. 6 eabc0726
Google Scholar
-
图 1 Ti1–xNiSb (0 ≤ x ≤ 0.25) 和Ti1–x–yScyNiSb (x = 0.10, 0.15; y = 0.03, 0.05) 样品的XRD图谱(a), (c)与晶格常数(b), (d)
Fig. 1. XRD patterns (a), (c) and lattice constant (b), (d) of Ti1–xNiSb (0 ≤ x ≤ 0.25) and Ti1–x–yScyNiSb (x = 0.10, 0.15; y = 0.03, 0.05)
图 2 Ti0.85NiSb和Ti0.8Sc0.05NiSb样品的XPS能谱
Fig. 2. XPS spectra of Ti0.85NiSb and Ti0.8Sc0.05NiSb samples.
图 3 样品Ti0.8Sc0.05NiSb的SEM (a)和BSE (b) 图像 (插图为EDS面扫描元素分布图)
Fig. 3. SEM image (a) and BSE image (b) of the Ti0.8Sc0.05NiSb samples (The insets are the EDS elemental mappings).
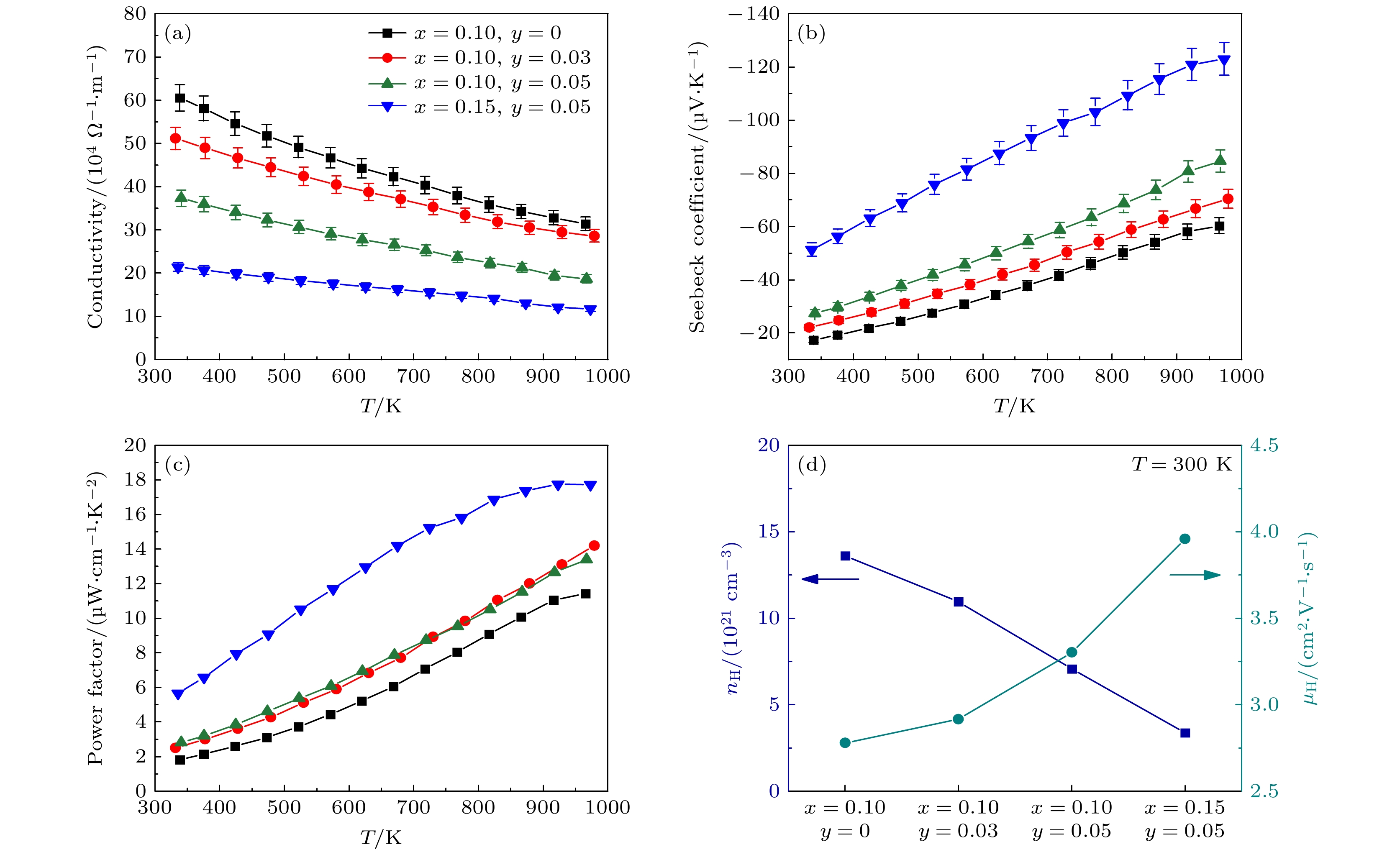
图 4 Ti1–x–yScyNiSb (x = 0.10, 0.15; y = 0.03, 0.05)的电输运特性随温度的变化 (a) 电导率σ; (b) 塞贝克系数S; (c) 功率因子. (d) Ti1–x–yScyNiSb样品的载流子浓度nH和迁移率μH
Fig. 4. Temperature dependent electrical transport properties of Ti1–x–yScyNiSb (x = 0.10, 0.15; y = 0.03, 0.05) samples: (a) Electrical conductivity σ; (b) Seebeck coefficients S; (c) power factor. (d) Room-temperature Hall carrier concentration nH and mobility μH of Ti1–x-yScyNiSb samples.
图 5 Ti1–x–yScyNiSb样品的塞贝克系数S随载流子浓度nH的变化
Fig. 5. Carrier concentration dependent Seebeck coefficient for Ti1–x–yScyNiSb samples at room temperature.
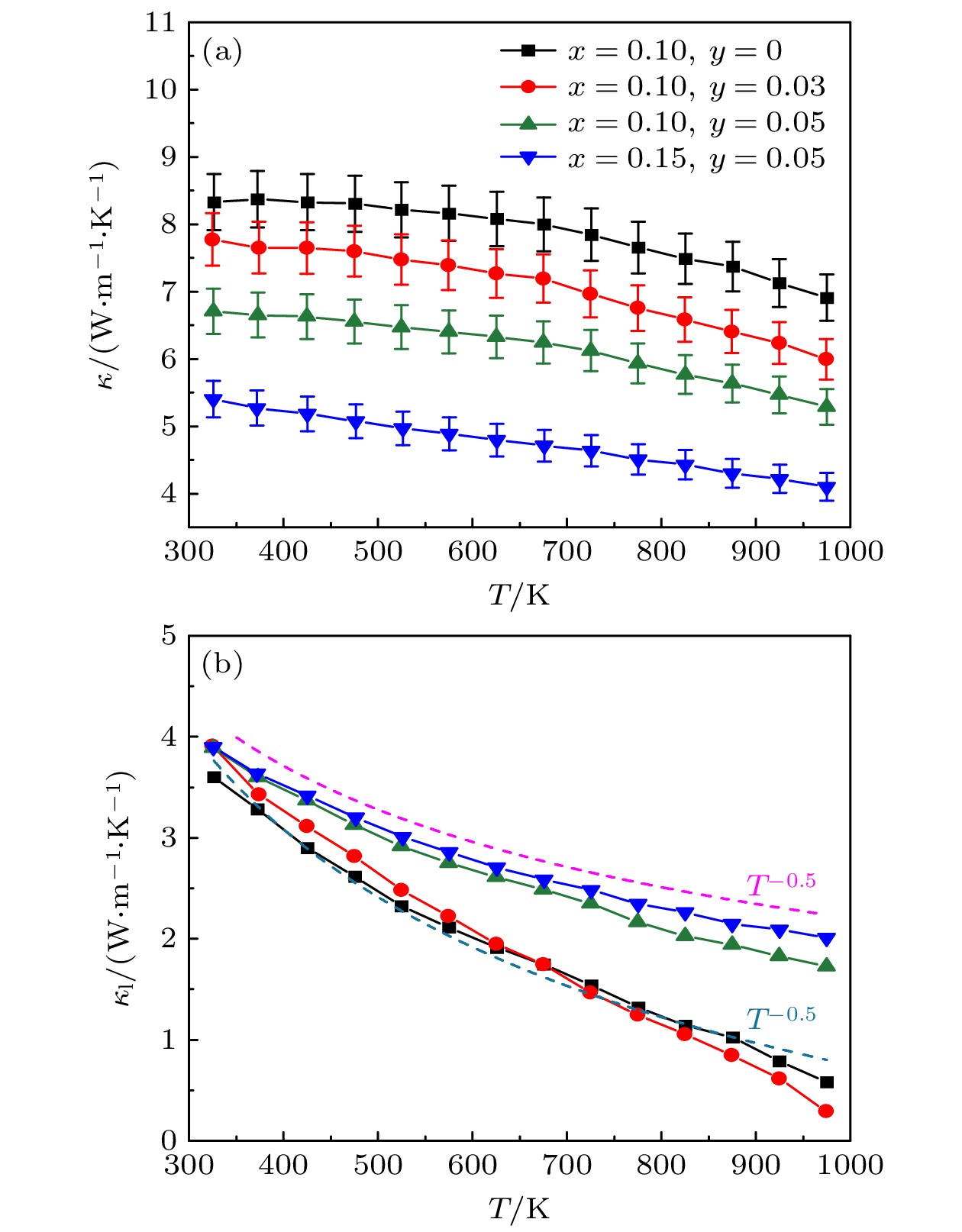
图 6 (a), (b) Ti1–x–yScyNiSb (x = 0.10, 0.15; y = 0.03, 0.05) 样品的总热导率κ和晶格热导率κl随温度的变化 (图(b)中的虚线为T–0.5关系)
Fig. 6. (a), (b) Temperature dependence of total thermal conductivity (κ) and lattice thermal conductivity (κl) of Ti1–x–yScyNiSb (x = 0.10, 0.15; y = 0.03, 0.05) samples (The dashed lines in Fig. (b) represent the T–0.5 relationship).
表 1 Ti1–x–yScyNiSb (x = 0.10, 0.15; y = 0.03, 0.05) 样品的名义成分和EDS实际成分
Table 1. Nominal and actual atomic contents for Ti1–x–yScyNiSb (x = 0.10, 0.15; y = 0.03, 0.05) detected by EDS.
名义成分 实际成分 Ti0.9NiSb Ti0.87NiSb1.04 Ti0.87Sc0.03NiSb Ti0.85Sc0.03NiSb1.02 Ti0.85Sc0.05NiSb Ti0.85Sc0.06NiSb1.15 Ti0.80Sc0.05NiSb Ti0.80Sc0.06NiSb1.04 
下载: 导出CSV
表 2 室温下Ti1–x–yScyNiSb (x = 0.10, 0.15; y = 0.03, 0.05) 样品的横波
${{v}}_{\text{l}}$ 和纵波声速${{v}}_{\text{t}}$ , 以及利用公式①计算得到的平均声速${{v}}_{\text{s}}$ Table 2. Measured longitudinal
${{v}}_{\text{l}}\text{}$ and transverse${{v}}_{\text{t}}$ sound velocities for Ti1–x–yScyNiSb (x = 0.10, 0.15; y = 0.03, 0.05) samples at room temperature. The average sound velocity${{v}}_{\text{s}}$ is calculated by the formula①样品 ${ {v} }_{{\rm{l}} }$/(m·s–1) ${v} _{{\rm{t}}}$/(m·s–1) ${v}_{{\rm{s}}}$/(m·s–1) Ti0.9NiSb 3085 5887 3451 Ti0.87Sc0.03NiSb 3094 5841 3458 Ti0.85Sc0.05NiSb 3100 5844 3464 Ti0.80Sc0.05NiSb 3121 5977 3491 注: ① ${ {v} }_{\text{s} }=\left[\dfrac{\text{1} }{\text{3} }\text{}\left(\dfrac{\text{1} }{ { {v} }_{\text{l} }^{\text{3} } }+\dfrac{\text{2} }{ { {v} }_{\text{t} }^{\text{3} } }\right)\right] ^{ {-1/3} }.$
下载: 导出CSV
-
[1] Bell L E 2008 Science 321 1457
Google Scholar
[2] Jia N, Cao J, Tan X Y, Dong J F, Liu H F, Tan C K I, Xu J W, Yan Q Y, Loh X J, Suwardi A 2021 Energy Environ. Sci. 21 100519
Google Scholar
[3] Min R A, Wang Y X, Jiang X, Chen R C, Kang H J, Guo E Y, Chen Z N, Yang X, Wang T M 2022 Chem. Eng. J. 449 137898
Google Scholar
[4] Joshi G, Dahal T, Chen S, Wang H Z, Shiomi J, Chen G, Ren Z F 2013 Nano Energy 2 82
Google Scholar
[5] Yu C, Zhu T J, Shi R Z, Zhang Y, Zhao X B, He J 2009 Acta Mater. 57 2757
Google Scholar
[6] Fu C G, Zhu T J, Liu Y T, Xie H H, Zhao X B 2015 Energy Environ. Sci. 8 216
Google Scholar
[7] Pei Y Z, Shi X Y, LaLonde A, Wang H, Chen L D, Snyder G J 2011 Nature 473 66
Google Scholar
[8] Fu C G, Zhu T J, Pei Y Z, Xie H H, Wang H, Snyder G J, Liu Y, Liu Y T, Zhao X B 2014 Adv. Energy Mater. 4 1400600
Google Scholar
[9] Tan C, Wang H X, Yao J, Chen T T, Wang L, Sun Y Q, Khan M, Wang H C, Wang C L 2022 J. Eur. Ceram. Soc. 42 7010
Google Scholar
[10] Biswas K, He J Q, Blum I D, Wu C I, Hogan T P, Seidman D N, Dravid V P, Kanatzidis M G 2012 Nature 489 414
Google Scholar
[11] Sun Y J, Shuai Z G, Wang D 2019 J. Phys. Chem. C 123 12001
Google Scholar
[12] He R, Gahlawat S, Guo C F, Chen S, Dahal T, Zhang H, Liu W S, Zhang Q, Chere E, White K, Ren Z F 2015 Phys. Status. Solidi. A 212 2191
Google Scholar
[13] Graf T, Felser C, Parkin S S P 2011 Prog. Solid. State Ch. 39 1
Google Scholar
[14] Sakurada S, Shutoh N 2005 Appl. Phys. Lett. 86 082105
Google Scholar
[15] Uher C, Yang J, Hu S, Morelli D T, Meisner G P 1999 Phys. Rev. B 59 8615
Google Scholar
[16] 王鹏将, 康慧君, 杨雄, 刘颖, 程成, 王同敏 2022 无机材料学报 37 717
Google Scholar
Wang P J, Kang H J, Yang X, Liu Y, Cheng C, Wang T M 2022 J. Inorg. Mater. 37 717
Google Scholar
[17] Sekimoto T, Kurosaki K, Muta H, Yamanaka S 2006 Mater. Trans. 47 1445
Google Scholar
[18] Sekimoto T, Kurosaki K, Muta H, Yamanaka S 2005 Mater. Trans. 46 1481
Google Scholar
[19] Sekimoto T, Kurosaki K, Muta H, Yamanaka S 2007 Jpn. J. Appl. Phys. 46 L673
Google Scholar
[20] Huang Y, Hayashi K, Miyazaki Y 2020 Chem. Mater. 32 5173
Google Scholar
[21] Joshi G, He R, Engber M, Samsonidze G, Pantha T, Dahal E, Dahal K, Yang J, Lan Y C, Kozinsky B, Ren Z F 2014 Energy Environ. Sci. 7 4070
Google Scholar
[22] Zhu H T, Mao J, Li Y W, et al. 2019 Nat. Commun. 10 270
Google Scholar
[23] Xia K, Liu Y, Anand S, Snyder G J, Xin J, Yu J, Zhao X, Zhu T 2018 Adv. Funct. Mater. 28 1705845
Google Scholar
[24] Li S, Bai F X, Wang R F, Chen C, Li X F, Cao F, Yu B, Sui J H, Liu X J, Ren Z F, Zhang Q 2020 Ann. Phys. 532 1900440
Google Scholar
[25] Miranda J, Gruhn T 2022 J. Electron. Mater. 51 2043
Google Scholar
[26] Huang L H, Wang J C, Mo X B, Lei X B, Ma S D, Wang C, Zhang Q Y 2019 Materials 12 1637
Google Scholar
[27] Kainuma R, Umino R, Xu X, Han K, Omori T 2020 J. Phase. Equilibria. Diffus. 41 116
Google Scholar
[28] Romaka V V, Rogl P, Romaka L, Stadnyk Y, Melnychenko N, Grytsiv A, Falmbigl M, Skryabina N 2013 J. Solid State Chem. 197 103
Google Scholar
[29] Anand S, Xia K Y, Zhu T J, Wolverton C, Snyder G J 2018 Adv. Energy Mater. 8 1801409
Google Scholar
[30] Luo F, Wang J, Zhu C, He X, Zhang S, Wang J F, Liu H X, Sun Z G 2022 J. Mater. Chem. A 10 9655
Google Scholar
[31] Anand S, Xia K Y, Hegde V I, Aydemir U, Kocevski V, Zhu T J, Wolverton C, Snyder G J 2018 Energy Environ. Sci. 11 1480
Google Scholar
[32] Romaka V V, Rogl G, Grytsiv A, Rogl P 2020 Comput. Mater. Sci. 172 109307
Google Scholar
[33] Zhou M, Chen L D, Feng C D, Wang D L, Li J F 2007 J. Appl. Phys. 101 113714
Google Scholar
[34] Zhao D G, Wang L, Bo L, Wu D 2018 Metals 8 61
Google Scholar
[35] Tavassoli A, Failamani F, Grytsiv A, Rogl G, Heinrich P, Müller H, Bauer E, Zehetbauer M, Rogl P 2017 Acta Mater. 135 263
Google Scholar
[36] Kim H S, Gibbs Z M, Tang Y L, Wang H, Snyder G J 2015 APL Mater. 3 041506
Google Scholar
[37] 沈家骏, 方腾, 傅铁铮, 忻佳展, 赵新兵, 朱铁军 2019 无机材料学报 34 260
Google Scholar
Shen J J, Fang T, Fu T Z, Xin J Z, Zhao X B, Zhu T J 2019 J. Inorg. Mater. 34 260
Google Scholar
[38] Zhu T J, Yu G T, Xu J, Wu H J, Fu C G, Liu X H, He J Q, Zhao X B 2016 Adv. Electron. Mater. 2 1600171
Google Scholar
[39] Karati A, Hariharan V S, Ghosh S, Prasad A, Nagini M, Guruvidyathri K, Mallik R C, Shabadi R, Bichler L, Murty B S, Varadaraju U V 2020 Scr. Mater. 186 375
Google Scholar
[40] Hasan R, Park T, Kim S I, Kim H S, Jo S, Lee K H 2022 Adv. Energy Sustainability Res. 3 2100206
Google Scholar
[41] Zhang X Y, Bu Z L, Shi X M, Chen Z W, Lin S Q, Shan B, Wood M, Snyder A H, Chen L D, Snyder G J, Pei Y Z 2020 Sci. Adv. 6 eabc0726
Google Scholar
下载:
计量
- 文章访问数: 4506
- PDF下载量: 72
- 被引次数: 0
