耗散环境单量子点体系输运过程的量子速度极限研究

刘天; 李宗良; 张延惠; 蓝康

doi:10.7498/aps.72.20222159

摘要

基于量子点输运理论与Bures角度量的方法, 研究了耗散环境下单量子点系统输运过程中的量子速度极限特性. 结果表明: 由于隧穿过程存在库仑阻塞效应与量子相干效应,系统可加速能力随左侧隧穿概率有微小的变化; 然而, 系统可加速能力随右侧隧穿概率变化明显, 归因于动力学通道阻塞与共隧穿的共同效应. 能级差的增大使系统向目标态演化需要更长的时间, 从而改变系统的加速潜力以及随时间演化的震荡频率. 耗散环境中弛豫速率对系统可加速能力的影响不是单调的,存在一个有趣的转折点,当弛豫速率小于该点时,系统的可加速能力产生震荡变化,当弛豫速率大于该点时,加速潜力的变化受到了弛豫速率的单调抑制,弛豫速率的增大总体上抑制了系统的可加速能力.

关键词:

Abstract

We theoretically study the quantum speed limit (QSL) of the single dot system in dissipative environment based on quantum dot transport theory and Bures angle metric method. The theoretical results show that in the dissipative environment, different tunneling probabilities have different effects. The increase of left tunneling probability has a weak effect on the accelerating capability of the system, due to the Coulomb blocking effect and quantum coherence. On the other hand, the right tunneling probability has a significant influence on the accelerating capability of the system, the accelerating capability is promoted with the increase of right tunneling probability because of the effect of channel blocking and co-tunneling. The increase of energy displacement promotes the accelerating capability of the system and changes the oscillation frequency of the system, owing to its taking longer time for the system to evolve to a target state. The effect of the relaxation rate for the system's accelerating capability is not monotonic, there is an interesting turning point due to the change of electron layout number. When the relaxation rate is less than this point, the accelerating capability of the system will oscillate. When the relaxation rate is higher than this point, the change of accelerating capability is monotonically suppressed by the relaxation rate. In general, the increase of the relaxation rate weakens the acceleration capability of the system. Our results provide theoretical reference for studying the QSL time in a semiconductor device affected by numerous factors.

Keywords:

作者及机构信息

1.
山东师范大学物理与电子科学学院, 济南　250014

2.
山东大学物理学院, 晶体材料国家重点实验室, 济南　250100

通信作者: 张延惠, yhzhang@sdnu.edu.cn

基金项目: 国家自然科学基金(批准号: 11974217)资助的课题.

Authors and contacts

1.
School of Physics and Electronics, Shandong Normal University, Jinan 250014, China

2.
School of Physics, State Key Laboratory of Crystal Materials, Shandong University, Jinan 250100, China

Corresponding author: Zhang Yan-Hui, yhzhang@sdnu.edu.cn

Funds: Project supported by the Natural Science Foundation of Shandong Province(Grant No. 11974217).

文章全文 : translate this paragraph

参考文献

[1]	Poggi P M 2019 Phys. Rev. A 99 042116 Google Scholar
[2]	Marvian I, Spekkens R, Zanardi P 2016 Phys. Rev. A 93 052331 Google Scholar
[3]	Pires D P, Modi K, Celeri L C 2021 Phys. Rev. E 103 032105 Google Scholar
[4]	Negrneac V, Ali H, Muthusubramanian N, Battistel F, Sagastizabal R, Moreira M S, Marques J F, Vlothuizen W J, Beekman M, Zachariadis C, Haider N, Bruno A, DiCarlo L 2021 Phys. Rev. Lett. 126 220502 Google Scholar
[5]	Villamizar D V, Duzzioni E I 2015 Phys. Rev. A 92 042106 Google Scholar
[6]	Farhi E, Goldstone J, Gutmann S, Sipser M 1998 Phys. Rev. Lett. 81 5442 Google Scholar
[7]	Russell B, Stepney S 2014 Phys. Rev. A 90 012303 Google Scholar
[8]	Becker S, Datta N, Lami L, Rouze C 2021 Phys. Rev. Lett. 126 190504 Google Scholar
[9]	Xu Z Y, Luo S L, Yang W L, Liu C, Zhu S Q 2014 Phys. Rev. A 89 012307 Google Scholar
[10]	Liu H B, Yang W L, An J H, Xu Z Y 2016 Phys. Rev. A 93 020105 Google Scholar
[11]	Rossatto D Z, Pires D P, de Paula F M, de Saneto O P 2020 Phys. Rev. A 102 053716 Google Scholar
[12]	Hegerfeldt G C 2013 Phys. Rev. Lett. 111 260501 Google Scholar
[13]	Kobe D H, Aguilera-Navarro V C 1994 Phys. Rev. A 50 933 Google Scholar
[14]	Mandelstam L, Tamm I 1945 J. Phys. USSR 9 249
[15]	Margolus N, Levitin L B 1998 Phys. D 120 188 Google Scholar
[16]	Deffner S, Lutz E 2013 Phys. Rev. Lett. 111 010402 Google Scholar
[17]	Bagheri Harouni M 2021 Chin. Phys. B 30 090301 Google Scholar
[18]	冯海冉, 李鹏, 岳现房 2019 68 050201 Google Scholar Feng H R, Li P, Yue X F 2019 Acta Phys. Sin. 68 050201 Google Scholar
[19]	Du K Y, Ma Y J, Wu S X, Yu C S 2021 Chin. Phys. B 30 090308 Google Scholar
[20]	Huang J H, Qin L G, Chen G L, Hu L Y, Liu F 2022 Chin. Phys. B 31 110307 Google Scholar
[21]	孙舒宁, 郑雨军 2021 科学通报 66 1946 Google Scholar Sun S N, Zheng Y J 2021 Chin. Sci. Bull. 66 1946 Google Scholar
[22]	Cai X J, Zheng Y J 2016 Phys. Rev. A 94 042110
[23]	Sun S N, Zheng Y J 2019 Phys. Rev. Lett. 123 180403 Google Scholar
[24]	Sun S, Peng Y, Hu X, Zheng Y 2021 Phys. Rev. Lett. 127 100404 Google Scholar
[25]	Gurvitz S A 1997 Phys. Rev. B 56 15215 Google Scholar
[26]	Gurvitz S A, Fedichkin L, Mozyrsky D and Berman G P 2003 Phys. Rev. Lett. 91 066801 Google Scholar
[27]	Ouyang S H, Lam C H, You J Q 2010 Phys. Rev. B 81 075301 Google Scholar
[28]	Lan K, Du Q, Kang L S, Tang X, Jiang L J, Zhang Y H, Cai X J 2020 Phys. Rev. B 101 174302 Google Scholar
[29]	Jiang L J, Lan K, Lin Z Y, Zhang Y H 2021 Chin. Phys. B 30 040307 Google Scholar
[30]	Kang L S, Zhang Y H, Xu X L, Tang X 2017 Phys. Rev. B 96 235417 Google Scholar
[31]	Du Q, Lan K, Zhang Y H, Jiang L J 2020 Chin. Phys. B 29 030302 Google Scholar
[32]	Lin Z Y, Zhang Y H, L T, Li Z L 2022 Chin. Phys. B 31 070307 Google Scholar
[33]	Wu S X, Yu C S 2018 Phys. Rev. A 98 042132 Google Scholar
[34]	Hu X H, Sun S N, Zheng Y J 2020 Phys. Rev. A 101 042107 Google Scholar
[35]	蓝康, 杜倩, 康丽莎, 姜露静, 林振宇, 张延惠 2020 69 040504 Google Scholar Lan K, Du Q, Kang L S, Jiang L J, Lin Z Y, Zhang Y H 2020 Acta Phys. Sin. 69 040504 Google Scholar
[36]	栗军, 刘玉, 平婧, 叶银, 李新奇 2012 61 137202 Google Scholar Li J, Liu Y, Ping J, Ye Y, Li X Q 2012 Acta Phys. Sin. 61 137202 Google Scholar
[37]	Ektesabi A, Behzadi N and Faizi E 2017 Phys. Rev. A 95 022115 Google Scholar
[38]	Deffner S 2017 New J. Phys. 19 103018 Google Scholar
[39]	Deffner S and Campbell S 2017 J. Phys. A Math. Theor. 50 453001 Google Scholar
[40]	Cai X J and Zheng Y J 2017 Phys. Rev. A 95 052104 Google Scholar
[41]	Lu X, Zhang Y J and Xia Y J 2021 Chin. Phys. B 30 020301 Google Scholar
[42]	Lan K, Xie S J and Cai X J 2022 New J. Phys. 24 055003 Google Scholar

施引文献

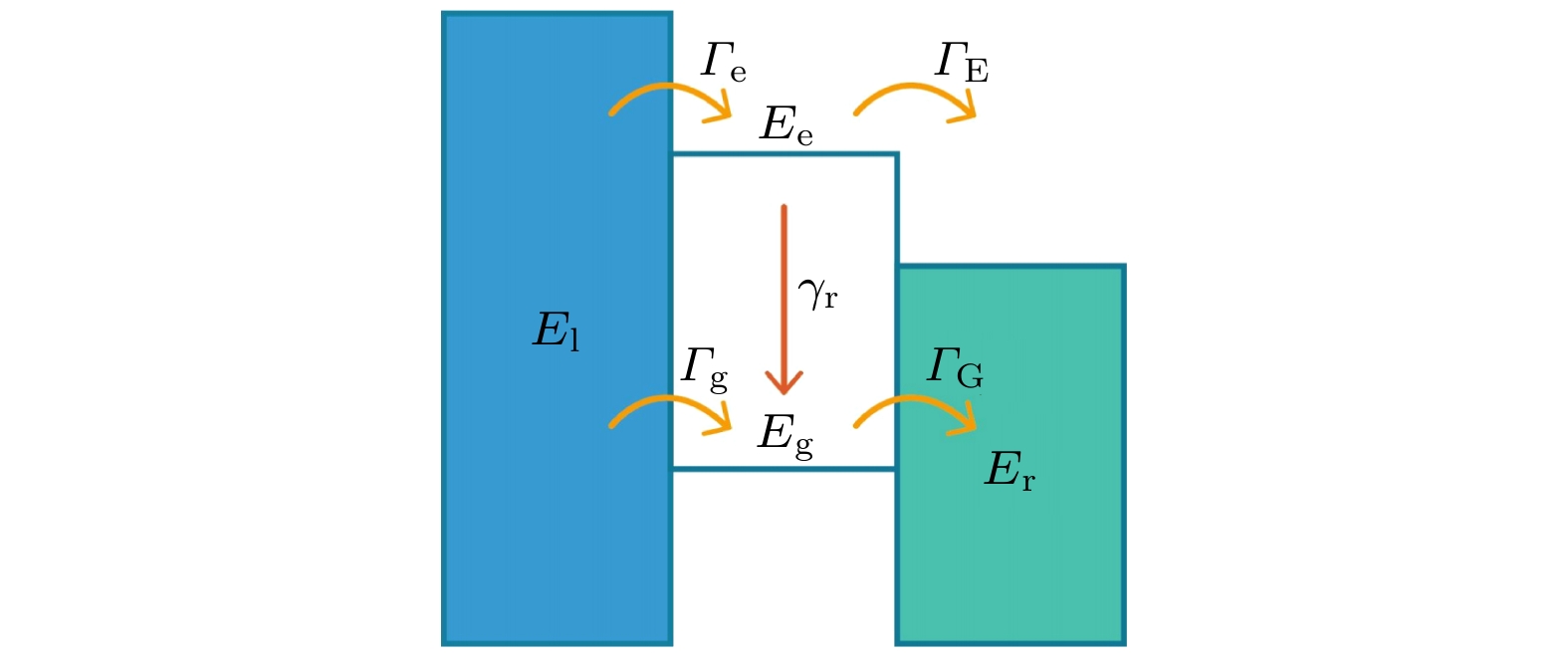
图 1 单量子点系统输运过程示意图, $ {E_{\text{e}}} $和$ {E_g} $表示激发态与基态能级, $ {E_{\text{l}}} $和$ {E_{\text{r}}} $为左右两侧化学势, $ {\varGamma _{{\text{e}}\left( {\text{g}} \right)}} $为左侧电子隧穿进入激发态(基态)能级的隧穿概率, $ {\varGamma _{{\text{E}}\left( {\text{G}} \right)}} $为激发态(基态)电子隧穿进入右侧电子库的隧穿概率

Fig. 1. The diagram of the single quantum dot system in transport process , $ {E_{\text{e}}} $and $ {E_g} $denotes two energy levels in quantum dot, $ {E_{\text{l}}} $ and$ {E_{\text{r}}} $denotes the left and right electrode potentials $ {\varGamma _{{\text{e}}\left( {\text{g}} \right)}} $ is the tunneling probability of the left electron tunneling into the excited(ground) state energy level, $ {\varGamma _{{\text{E}}\left( {\text{G}} \right)}} $ is the tunneling probability of the excited (ground) state electron tunneling into the right electron library.

下载: 全尺寸图片幻灯片

图 2 初态为g态与相干态下量子速度极限时间比值${{{\tau _{{\text{QSL}}}}} /\tau }$随驱动时间变化图　(a)初态为g态时$ {{{\tau _{{\text{QSL}}}}}/ \tau } $随驱动时间的变化; (b)初态为相干态时$ {{{\tau _{{\text{QSL}}}}} \mathord{\left/ {\vphantom {{{\tau _{{\text{QSL}}}}} \tau }} \right. } \tau } $随驱动时间的变化, 左侧量子点与电子库耦合强度${\varOmega _{\text{r}}} = 1$, 电子的隧穿概率$ {\varGamma _{\text{E}}} = 0.5 $

Fig. 2. The ratio of the quantum speed limit time $ {{{\tau _{{\text{QSL}}}}} / \tau } $ varies with the driving time in the initial g state and the superposition state: (a) The change of the$ {{{\tau _{{\text{QSL}}}}}/\tau } $with driving time when the initial state is coherent state; (b)the change of the $ {{{\tau _{{\text{QSL}}}}} /\tau } $with driving time when the initial state is superposition state ; the left coupling strength parameter ${\varOmega _{\text{r}}} = 1$, tunneling probability of electrons${\varGamma _{\text{E}}} = 0.5$.

下载: 全尺寸图片幻灯片

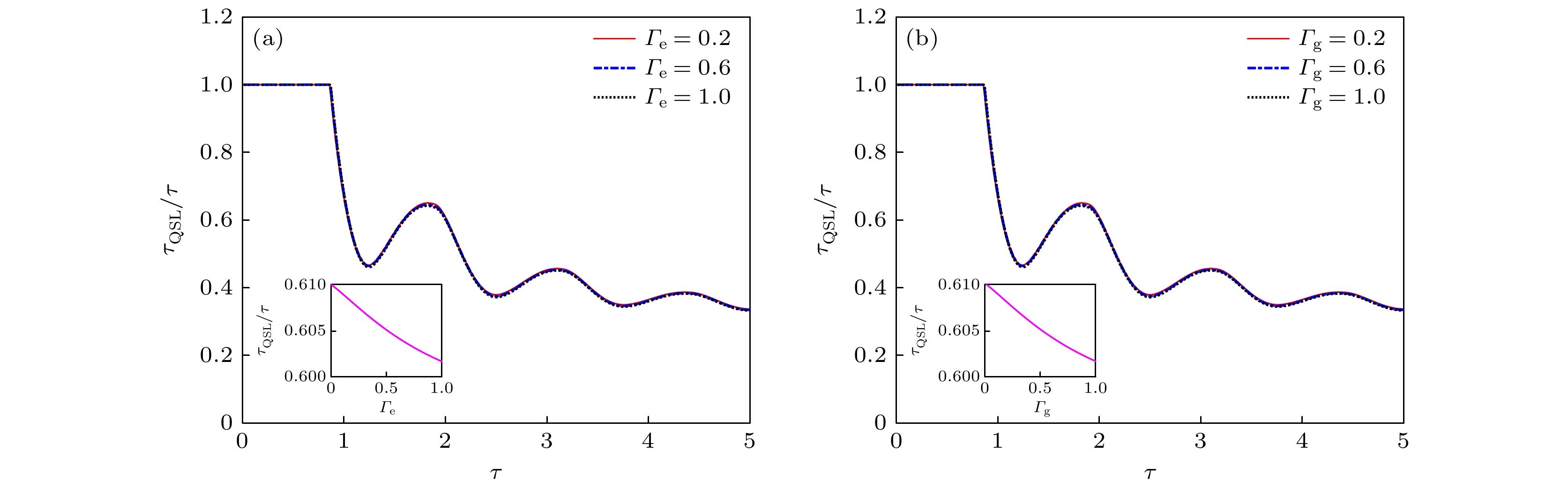
图 3 单量子点系统的速度极限时间比值$ {{{\tau _{{\text{QSL}}}}} / \tau } $随左侧隧穿概率与驱动时间的变化图　(a)不同左侧激发态隧穿概影响下$ {{{\tau _{{\text{QSL}}}}} / \tau } $随驱动时间变化; (b)不同左侧基态隧穿概率影响下$ {{{\tau _{{\text{QSL}}}}} / \tau } $随驱动时间变化, 量子点与左侧电子库耦合强度${\varOmega _{\text{r}}} = 1$, 能级差$\varepsilon = 5{\varOmega _{\text{r}}}$

Fig. 3. The diagram of the quantum speed limit time ratio $ {{{\tau _{{\text{QSL}}}}}/ \tau } $as a function of left tunneling probability and driving time for a single quantum dot system: (a) Variation of $ {{{\tau _{{\text{QSL}}}}}/\tau } $with driving time under the influence of left different tunneling probabilities into excited states; (b) variation of $ {{{\tau _{{\text{QSL}}}}} / \tau } $with driving time under the influence of left different tunneling probabilities into ground states, the left coupling strength parameter ${\varOmega _{\text{r}}} = 1$, the energy displacement $\varepsilon = 5{\varOmega _{\text{r}}}$.

下载: 全尺寸图片幻灯片

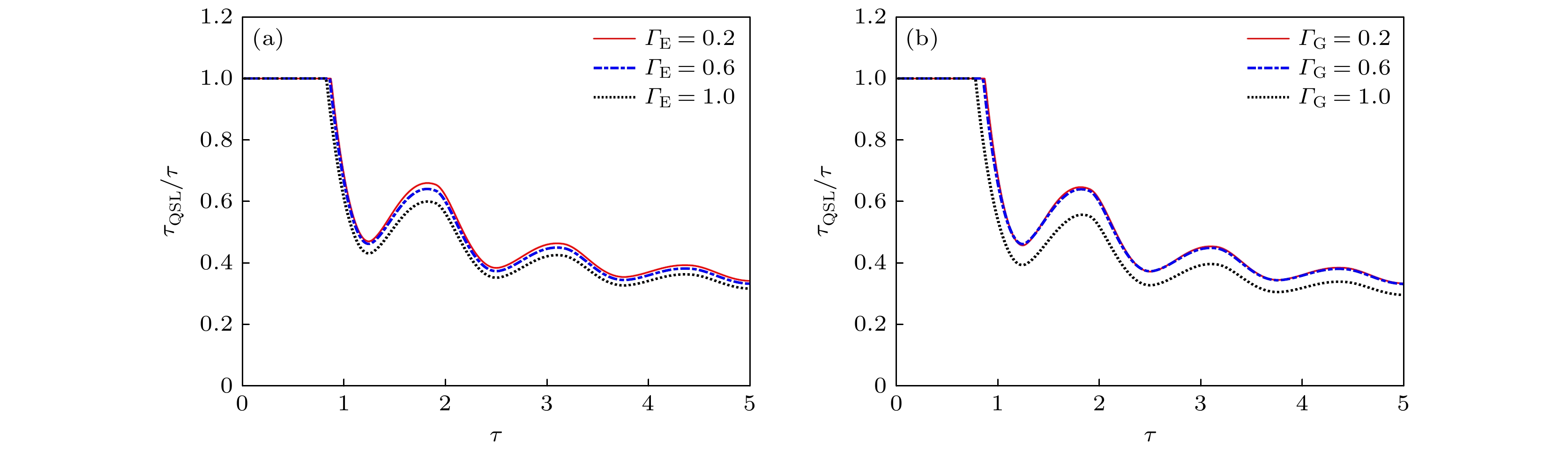
图 4 单量子点系统的速度极限时间比值$ {{{\tau _{{\text{QSL}}}}} / \tau } $随右侧隧穿概率与驱动时间的变化图　(a)不同右侧激发态隧穿概率影响下$ {{{\tau _{{\text{QSL}}}}} / \tau } $随驱动时间的变化; (b)不同右侧基态隧穿概率影响下$ {{{\tau _{{\text{QSL}}}}} / \tau } $随驱动时间的变化. 量子点与左侧电子库耦合强度${\varOmega _{\text{r}}} = 1$, 能极差$\varepsilon = 5{\varOmega _{\text{r}}}$

Fig. 4. The diagram of the quantum speed limit time ratio $ {{{\tau _{{\text{QSL}}}}} / \tau } $as a function of right tunneling probability and driving time for a single quantum dot system: (a) Variation of $ {{{\tau _{{\text{QSL}}}}} / \tau } $with driving time under the influence of right different tunneling probabilities from excited states ; (b) variation of $ {{{\tau _{{\text{QSL}}}}} / \tau } $with driving time under the influence of right different tunneling probabilities from ground states.The left coupling strength parameter ${\varOmega _{\text{r}}} = 1$, the energy displacement $\varepsilon = 5{\varOmega _{\text{r}}}$.

下载: 全尺寸图片幻灯片

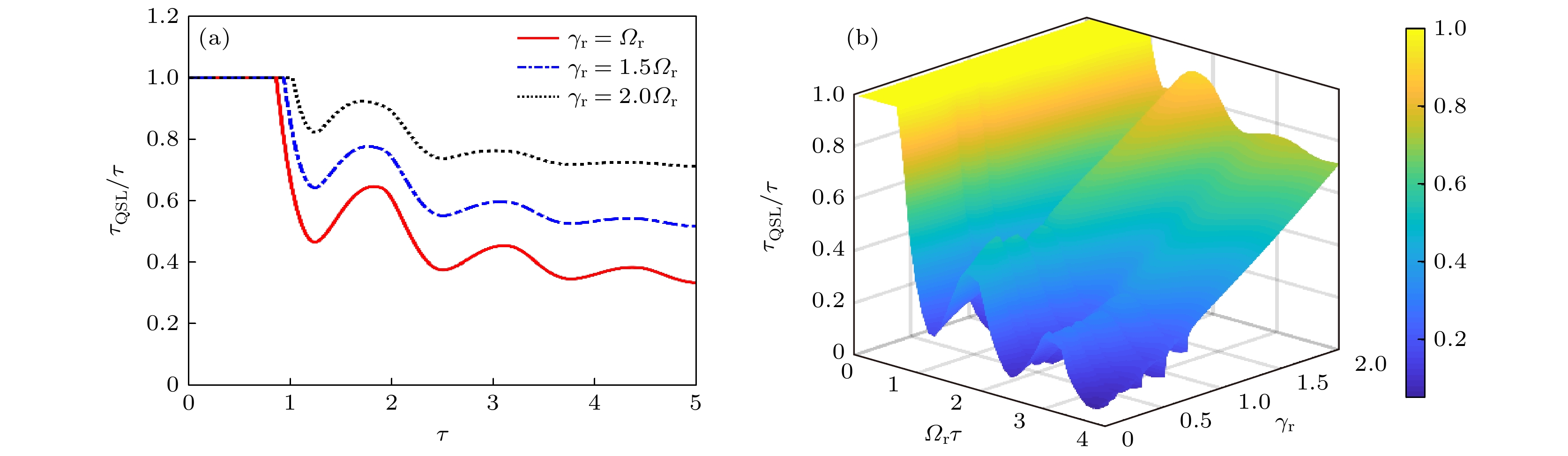
图 5 单量子点系统的速度极限时间比值$ {{{\tau _{{\text{QSL}}}}} / \tau } $随弛豫速率与驱动时间的变化图　(a) 不同弛豫速率影响下$ {{{\tau _{{\text{QSL}}}}} / \tau } $随驱动时间的变化; (b) $ {{{\tau _{{\text{QSL}}}}} / \tau } $随弛豫速率$ {\gamma _r} $与驱动时间的三维变化图. 量子点与左侧电子库耦合强度${\varOmega _{\text{r}}} = 1$, 能极差$ \varepsilon = 5{\varOmega _{\text{r}}} $

Fig. 5. The diagram of the quantum speed limit time ratio $ {{{\tau _{{\text{QSL}}}}} / \tau } $as a function of relaxation rates and driving time for a single quantum dot system:(a) Variation of $ {{{\tau _{{\text{QSL}}}}} / \tau } $with driving time under different relaxation rates ; (b) three-dimensional diagram of $ {{{\tau _{{\text{QSL}}}}} / \tau } $ as a function of relaxation rate and driving time. The left coupling strength parameter ${\varOmega _{\text{r}}} = 1$, the energy displacement$\varepsilon = 5{\varOmega _{\text{r}}}$.

下载: 全尺寸图片幻灯片

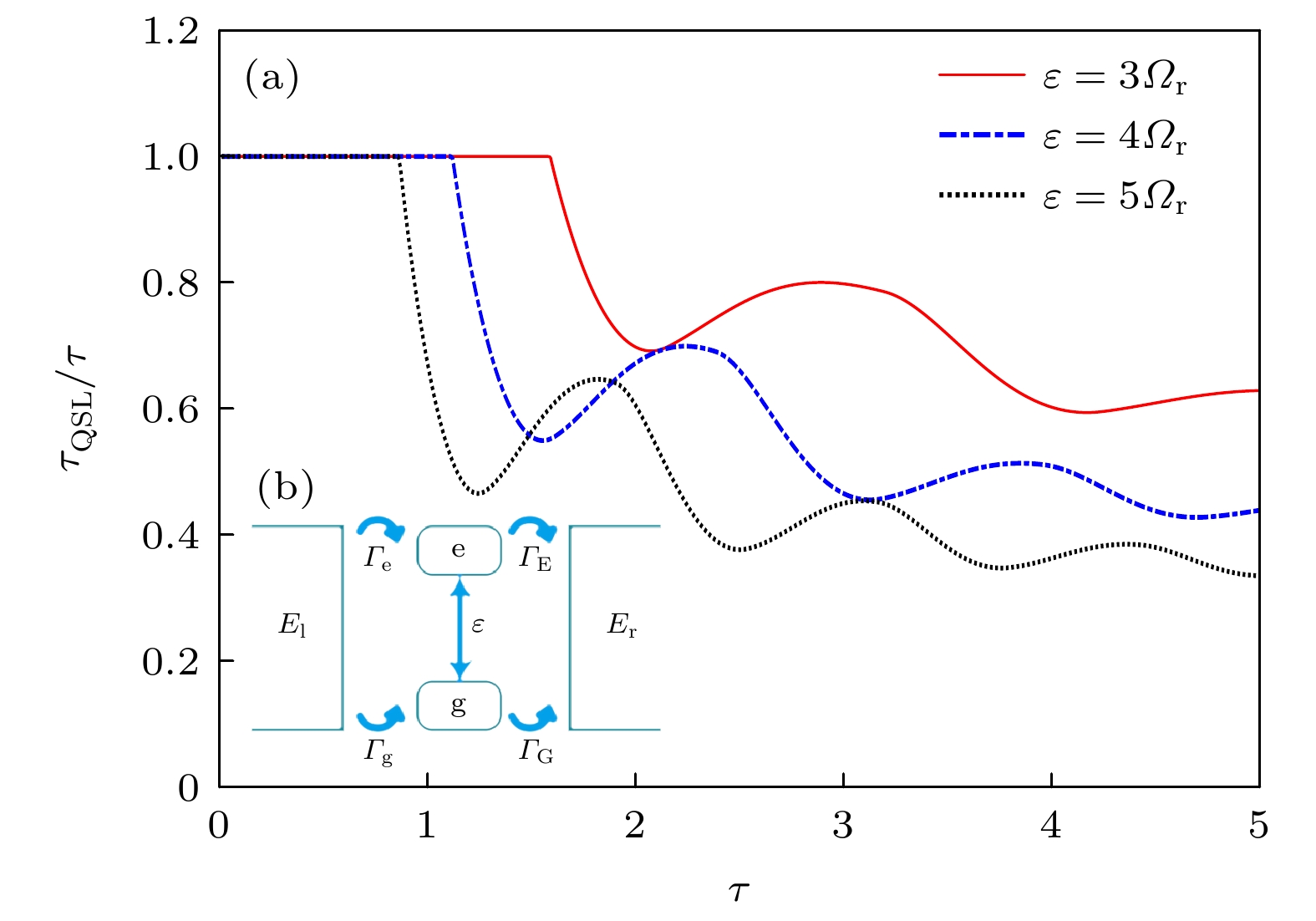
图 6 单量子点系统的速度极限时间比值$ {{{\tau _{{\text{QSL}}}}} / \tau } $随能级差$ \varepsilon $与驱动时间的变化图　(a)不同能级差$ \varepsilon $影响下的$ {{{\tau _{{\text{QSL}}}}} / \tau } $随驱动时间变化; (b)能级差产生跃迁原理图. 量子点与左侧电子库耦合强度${\varOmega _{\text{r}}} = 1$, $ {\varGamma _{\text{E}}} = 0.5 $

Fig. 6. The diagram of the quantum speed limit time ratio $ {{{\tau _{{\text{QSL}}}}} / \tau } $ as a function of energy displacement $ \varepsilon $ and driving time for a single quantum dot system: (a) Variation of $ {{{\tau _{{\text{QSL}}}}} / \tau } $ with driving time under different energy displacement $ \varepsilon $; (b) the schematic diagram of transition generation by difference energy level. The left coupling strength parameter ${\varOmega _{\text{r}}} = 1$, Tunneling probability of electrons $ {\varGamma _{\text{E}}} = 0.5 $.

下载: 全尺寸图片幻灯片

map

[1]	Poggi P M 2019 Phys. Rev. A 99 042116 Google Scholar
[2]	Marvian I, Spekkens R, Zanardi P 2016 Phys. Rev. A 93 052331 Google Scholar
[3]	Pires D P, Modi K, Celeri L C 2021 Phys. Rev. E 103 032105 Google Scholar
[4]	Negrneac V, Ali H, Muthusubramanian N, Battistel F, Sagastizabal R, Moreira M S, Marques J F, Vlothuizen W J, Beekman M, Zachariadis C, Haider N, Bruno A, DiCarlo L 2021 Phys. Rev. Lett. 126 220502 Google Scholar
[5]	Villamizar D V, Duzzioni E I 2015 Phys. Rev. A 92 042106 Google Scholar
[6]	Farhi E, Goldstone J, Gutmann S, Sipser M 1998 Phys. Rev. Lett. 81 5442 Google Scholar
[7]	Russell B, Stepney S 2014 Phys. Rev. A 90 012303 Google Scholar
[8]	Becker S, Datta N, Lami L, Rouze C 2021 Phys. Rev. Lett. 126 190504 Google Scholar
[9]	Xu Z Y, Luo S L, Yang W L, Liu C, Zhu S Q 2014 Phys. Rev. A 89 012307 Google Scholar
[10]	Liu H B, Yang W L, An J H, Xu Z Y 2016 Phys. Rev. A 93 020105 Google Scholar
[11]	Rossatto D Z, Pires D P, de Paula F M, de Saneto O P 2020 Phys. Rev. A 102 053716 Google Scholar
[12]	Hegerfeldt G C 2013 Phys. Rev. Lett. 111 260501 Google Scholar
[13]	Kobe D H, Aguilera-Navarro V C 1994 Phys. Rev. A 50 933 Google Scholar
[14]	Mandelstam L, Tamm I 1945 J. Phys. USSR 9 249
[15]	Margolus N, Levitin L B 1998 Phys. D 120 188 Google Scholar
[16]	Deffner S, Lutz E 2013 Phys. Rev. Lett. 111 010402 Google Scholar
[17]	Bagheri Harouni M 2021 Chin. Phys. B 30 090301 Google Scholar
[18]	冯海冉, 李鹏, 岳现房 2019 68 050201 Google Scholar Feng H R, Li P, Yue X F 2019 Acta Phys. Sin. 68 050201 Google Scholar
[19]	Du K Y, Ma Y J, Wu S X, Yu C S 2021 Chin. Phys. B 30 090308 Google Scholar
[20]	Huang J H, Qin L G, Chen G L, Hu L Y, Liu F 2022 Chin. Phys. B 31 110307 Google Scholar
[21]	孙舒宁, 郑雨军 2021 科学通报 66 1946 Google Scholar Sun S N, Zheng Y J 2021 Chin. Sci. Bull. 66 1946 Google Scholar
[22]	Cai X J, Zheng Y J 2016 Phys. Rev. A 94 042110
[23]	Sun S N, Zheng Y J 2019 Phys. Rev. Lett. 123 180403 Google Scholar
[24]	Sun S, Peng Y, Hu X, Zheng Y 2021 Phys. Rev. Lett. 127 100404 Google Scholar
[25]	Gurvitz S A 1997 Phys. Rev. B 56 15215 Google Scholar
[26]	Gurvitz S A, Fedichkin L, Mozyrsky D and Berman G P 2003 Phys. Rev. Lett. 91 066801 Google Scholar
[27]	Ouyang S H, Lam C H, You J Q 2010 Phys. Rev. B 81 075301 Google Scholar
[28]	Lan K, Du Q, Kang L S, Tang X, Jiang L J, Zhang Y H, Cai X J 2020 Phys. Rev. B 101 174302 Google Scholar
[29]	Jiang L J, Lan K, Lin Z Y, Zhang Y H 2021 Chin. Phys. B 30 040307 Google Scholar
[30]	Kang L S, Zhang Y H, Xu X L, Tang X 2017 Phys. Rev. B 96 235417 Google Scholar
[31]	Du Q, Lan K, Zhang Y H, Jiang L J 2020 Chin. Phys. B 29 030302 Google Scholar
[32]	Lin Z Y, Zhang Y H, L T, Li Z L 2022 Chin. Phys. B 31 070307 Google Scholar
[33]	Wu S X, Yu C S 2018 Phys. Rev. A 98 042132 Google Scholar
[34]	Hu X H, Sun S N, Zheng Y J 2020 Phys. Rev. A 101 042107 Google Scholar
[35]	蓝康, 杜倩, 康丽莎, 姜露静, 林振宇, 张延惠 2020 69 040504 Google Scholar Lan K, Du Q, Kang L S, Jiang L J, Lin Z Y, Zhang Y H 2020 Acta Phys. Sin. 69 040504 Google Scholar
[36]	栗军, 刘玉, 平婧, 叶银, 李新奇 2012 61 137202 Google Scholar Li J, Liu Y, Ping J, Ye Y, Li X Q 2012 Acta Phys. Sin. 61 137202 Google Scholar
[37]	Ektesabi A, Behzadi N and Faizi E 2017 Phys. Rev. A 95 022115 Google Scholar
[38]	Deffner S 2017 New J. Phys. 19 103018 Google Scholar
[39]	Deffner S and Campbell S 2017 J. Phys. A Math. Theor. 50 453001 Google Scholar
[40]	Cai X J and Zheng Y J 2017 Phys. Rev. A 95 052104 Google Scholar
[41]	Lu X, Zhang Y J and Xia Y J 2021 Chin. Phys. B 30 020301 Google Scholar
[42]	Lan K, Xie S J and Cai X J 2022 New J. Phys. 24 055003 Google Scholar

[1]	高建华, 盛欣力, 王群, 庄鹏飞. 费米子的相对论自旋输运理论. , 2023, 72(11): 112501. doi: 10.7498/aps.72.20222470
[2]	丁锦廷, 胡沛佳, 郭爱敏. 线缺陷石墨烯纳米带的电输运研究. , 2023, 72(15): 157301. doi: 10.7498/aps.72.20230502
[3]	方静云, 孙庆丰. 石墨烯p-n结在磁场中的电输运热耗散. , 2022, 71(12): 127203. doi: 10.7498/aps.71.20220029
[4]	胡海涛, 郭爱敏. 双层硼烯纳米带的量子输运研究. , 2022, 71(22): 227301. doi: 10.7498/aps.71.20221304
[5]	尚向军, 李叔伦, 马奔, 陈瑶, 何小武, 倪海桥, 牛智川. 量子点单光子源的光纤耦合. , 2021, 70(8): 087801. doi: 10.7498/aps.70.20201605
[6]	李斌, 苗向阳. 单个CsPbBr₃钙钛矿量子点的荧光闪烁特性. , 2021, 70(20): 207802. doi: 10.7498/aps.70.20210908
[7]	闫婕, 魏苗苗, 邢燕霞. HgTe/CdTe量子阱中自旋拓扑态的退相干效应. , 2019, 68(22): 227301. doi: 10.7498/aps.68.20191072
[8]	吴歆宇, 韩伟华, 杨富华. 硅纳米结构晶体管中与杂质量子点相关的量子输运. , 2019, 68(8): 087301. doi: 10.7498/aps.68.20190095
[9]	冯海冉, 李鹏, 岳现房. 初态对线型分子体系量子速度极限度量的影响. , 2019, 68(5): 050201. doi: 10.7498/aps.68.20181942
[10]	闫瑞, 吴泽文, 谢稳泽, 李丹, 王音. 导线非共线的分子器件输运性质的第一性原理研究. , 2018, 67(9): 097301. doi: 10.7498/aps.67.20172221
[11]	李兆国, 张帅, 宋凤麒. 拓扑绝缘体的普适电导涨落. , 2015, 64(9): 097202. doi: 10.7498/aps.64.097202
[12]	王早, 张国峰, 李斌, 陈瑞云, 秦成兵, 肖连团, 贾锁堂. 利用N型半导体纳米材料抑制单量子点的荧光闪烁特性. , 2015, 64(24): 247803. doi: 10.7498/aps.64.247803
[13]	孙伟峰. (InAs)1/(GaSb)1超晶格原子链的第一原理研究. , 2012, 61(11): 117104. doi: 10.7498/aps.61.117104
[14]	张彩霞, 郭虹, 杨致, 骆游桦. 三明治结构Tan(B3N3H6)n+1 团簇的磁性和量子输运性质. , 2012, 61(19): 193601. doi: 10.7498/aps.61.193601
[15]	陈宇, 邹健, 李军刚, 邵彬. 耗散环境下三原子之间稳定纠缠的量子反馈控制. , 2010, 59(12): 8365-8370. doi: 10.7498/aps.59.8365
[16]	潘长宁, 赵学辉, 杨迪武, 方卯发. 耗散环境下原子-库场相互作用系统中原子的偶极压缩特性. , 2010, 59(10): 6814-6818. doi: 10.7498/aps.59.6814
[17]	付邦, 邓文基. 任意正多边形量子环自旋输运的普遍解. , 2010, 59(4): 2739-2745. doi: 10.7498/aps.59.2739
[18]	李鹏, 邓文基. 正多边形量子环自旋输运的严格解. , 2009, 58(4): 2713-2719. doi: 10.7498/aps.58.2713
[19]	尹永琦, 李华, 马佳宁, 贺泽龙, 王选章. 多端耦合量子点分子桥的量子输运特性研究. , 2009, 58(6): 4162-4167. doi: 10.7498/aps.58.4162
[20]	邓宇翔, 颜晓红, 唐娜斯. 量子点环的电子输运研究. , 2006, 55(4): 2027-2032. doi: 10.7498/aps.55.2027

计量

文章访问数: 2814
PDF下载量: 69
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

耗散环境单量子点体系输运过程的量子速度极限研究