-
后随X射线望远镜(follow-up X-ray telescope, FXT)是爱因斯坦探针卫星的主要载荷之一. 为了获取高信噪比的数据, 实现对观测天体的高精度定位, FXT使用Wolter-I型X射线聚焦光学系统, 该系统一直是X 射线空间天文观测中的重要设备. 根据Wolter-I型的聚焦原理, 结合实际的加工特点, 利用蒙特卡罗模拟算法对影响光学成像质量的几个关键参量, 如表面粗糙度、面形误差进行了模拟, 结合模拟结果对各参量的作用效果进行了分析. 之后利用PANTER实验室提供的聚焦镜性能测试结果对模拟方法进行了验证, 同时对面形误差参量进行了限制. 最终聚焦镜结构热控件半能量宽度(half energy width, HEW)模拟与实测结果基本一致. 该模拟过程可以很有效地应用于聚焦镜加工工艺的摸索, 为FXT的聚焦镜测试和标定工作提供参考. 结合实测标定数据, 该模拟方法生成的有效面积、渐晕和点扩散函数等可用于在轨观测标定数据库.
-
关键词:
- 爱因斯坦探针卫星 /
- 后随X射线望远镜 /
- Wolter-I型X射线聚焦镜 /
- 真实面形模拟
The Follow-up X-ray Telescope (FXT) is one of the main payloads on board the Einstein probe satellite. In order to obtain data with high signal-to-noise ratio and realize high-precision positioning of the sources, FXT adopts the Wolter-I X-ray focusing optical system which has been wildly used in X-ray astronomy. According to the principle of Wolter-I and combining the actual manufacture characteristics, we simulate several key parameters affecting the optical quality by Monte Carlo simulation algorithm, such as surface roughness Root-Mean Square (RMS) and surface profile error. The effect of each parameter is analyzed according to the simulation results. Then, the simulation method is verified by the test results of the focusing mirrors provided by PANTER laboratory, and the surface profile error parameters are restricted. The simulation results of the half energy width of the structural-thermal module mirror are basically consistent with the test results. This method can be effectively applied to the later study of focusing mirror manufacture and can accumulate experience for testing and calibrating FXT focusing mirrors. Furthermore, combining the tested calibration data, some key performance of the mirrors can be obtained by this simulation method, such as the effective area, vignetting and the point spread function, which can compose the on-orbit calibration database.-
Keywords:
- Einstein probe /
- follow-up X-ray telescope /
- Wolter-I X-ray focusing mirror /
- simulation of actual surface
[1] Giacconi R, Branduardi G, Briel U, Epstein A, Fabricant D, Feigelson E, Forman W, Gorenstein P, Grindlay J, Gursky H, Harnden F R, Henry J P, Jones C, Kellogg E, Koch D, Murray S, Schreier E, Seward F, Tananbaum H, Topka K, Van Speybroeck L, Holt S S, Becker R H, Boldt E A, Serlemitsos P J, Clark G, Canizares C, Markert T, Novick R, Helfand D, Long K 1985 Astrophys. J. 230 540
Google Scholar
[2] Weisskopf M C, Tananbaum H D, Speybroeck L, O’Dell S L 2000 Proc. SPIE 4012 0277
Google Scholar
[3] Jansen F, Lumb D, Altieri B, Clavel J, Ehle M, Gabriel C, Guainazzi M, Gondoin P, Much R, Munoz R, Santos M, Schartel N, Texier D, Vacanti G 2000 Astron. Astrophys. 365 L1-L6
Google Scholar
[4] Predehl P 2017 Astron. Nachr. 338 159
Google Scholar
[5] Merloni A, Predehl P, Becker W, Bohringer H, Boller T, Brunner H, Brusa M, Dennerl K, Freyberg M, Friedrich P, Georgakakis A, Haberl F, Hasinger G, Meidinger N, Mohr J, Nandra K, Rau A, Reiprich T H, Robrade J, Salvato M, Santangelo A, Sasaki M, Schwope A, Wilms J, German eROSITA Consortium 2012 Casopis Lekaru Ceskych 99 1280
Google Scholar
[6] Li T P 2007 Nucl. Phys. B. Proc. Suppl. 166 131
Google Scholar
[7] Zhang S N, Li T P, Lu F J, et al. 2020 Sci. Chin.: Phys., Mech. Astron. 63 249502
Google Scholar
[8] Yuan W M, Zhang C, Ling Z X, Zhao D H, Wang W X, Chen Y, Lu F J, Zhang S N, Cui W 2018 Proc. SPIE 10699 1069925
Google Scholar
[9] Zhang S N, Santangelo A, Feroci M, et al. 2018 Sci. Chin.: Phys., Mech. Astron. 62 029502
Google Scholar
[10] 强鹏飞, 盛立志, 李林淼, 闫永清, 刘哲, 周晓红 2018 68 160702
Google Scholar
Qiang P F, Sheng L Z, Li L M, Yan Y Q, Liu Z, Zhou X H 2018 Acta Phys. Sin. 68 160702
Google Scholar
[11] Zhao D H, Zhang C, Yuan W M, Zhang S N, Willingale R, Ling Z X 2017 Exp. Astron. 43 267
Google Scholar
[12] Chen Y, Cui W W, Han D W, et al. 2020 Proc. SPIE 11444 114445b
Google Scholar
[13] Bernal J D 1935 Nature 136 661
Google Scholar
[14] Wolter H 1975 Ann. Phys. 10 94
[15] Zhang X Y, Shui P, Huang L W, Chen S L, Xu L H 2017 Int. J. Aerosp. Eng. 2017 8561830
Google Scholar
[16] 周庆勇, 魏子卿, 姜坤, 邓楼楼, 刘思伟, 姬剑锋, 任红飞, 王奕迪, 马高峰 2018 67 050701
Google Scholar
Zhou Q Y, Wei Z Q, Jiang K, Deng L L, Liu S W, Ji J F, Ren H F, Wang Y D, Ma G F 2018 Acta Phys. Sin. 67 050701
Google Scholar
[17] Angel J 1979 Astrophys. J. 233 364
Google Scholar
[18] Zhu Y X, Lu J B, Yang Y J, Cong M, Sheng L Z, Qiang P F, Cui W W, Zhang Z L, Wang Y S, Han D W, Li W, Wang J, Huo J, Li M S, Zhao X F, Yu N, Song Z Y, Ma J, Lv Z H, Zhao Z J, Wang H, Hou D J, Chen C, Chen T X, Yang X T, Luo L D, Lu B, Xu J J, Chen Y H, Chen Y 2021 Opt. Eng. 60 025102
Google Scholar
[19] 张星, 王娟, 张艺, 杨彦佶, 陈勇, 文健 2020 光子学报 49 0512002
Google Scholar
Zhang X, Wang J, Zhang Y, Yang Y J, Chen Y, Wen J 2020 Acta Photon. Sin. 49 0512002
Google Scholar
[20] 赵子健, 王于仨, 张留洋, 陈灿, 马佳 2019 光学精密工程 27 2331
Google Scholar
Zhao Z J, Wang Y S, Zhang L Y, Chen C, Ma J 2019 Opt. Precis. Eng. 27 2331
Google Scholar
[21] 李林森, 强鹏飞, 盛立志, 刘哲, 周晓红, 赵宝升, 张淳民 2018 67 200701
Google Scholar
Li L S, Qiang P F, Sheng L Z, Liu Z, Zhou X H, Zhao B S, Zhang C M 2018 Acta Phys. Sin. 67 200701
Google Scholar
[22] Laine R, Giralt R, Zobl R, de Korte P A, Bleeker J A M 1979 Proc. SPIE 184 181
Google Scholar
[23] Hunter W R, Michels D J, Fleetwood C M, Mangus J D, Bach B W 1980 Appl. Opt. 19 2128
Google Scholar
[24] Jin Y, Feng X, Li D, Xue J D, Wang B, Yang Y J, Ding F 2020 Optik 218 165022
Google Scholar
[25] Stover J C 2012 Optical Scattering: Measurement and analysis (SPIE) pp4–10
[26] Canestrari R, Spiga D, Pareschi G 2006 Proc. SPIE 6266 626613
Google Scholar
[27] Church L, Jenkinson H, Zavada A, Zavada J 1979 Opt. Eng. 18 182125
Google Scholar
[28] Church L, Takacs P Z 1986 Proc. SPIE 0640 126
Google Scholar
[29] Spiga D, Cusumano G, Pareschi G 2007 Proc. SPIE 6688 66880H
Google Scholar
[30] Qi L Q, Li Gang, Xu Y P, Zhang J, Yang Y J, Sheng L Z, Basso S, Campana R, Chen Y, De Rosa A, Pareschi G, Qiang P F, Santangelo A, Sironi G, Song L M, Spiga D, Tagliaferri G, Wang J, Wilms J, Zhang Y, Lu F J 2020 Nucl. Instrum. Methods Phys. Res., Sect. A 963 163702
Google Scholar
[31] Spiga D, Raimondi L, Svetina C, Zangrando M 2013 Nucl. Instrum. Methods Phys. Res., Sect. A 710 125
Google Scholar
[32] Zombeck M V, Braeuninger H, Ondrusch A, Predehl P 1981 Proc. SPIE 316 174
Google Scholar
[33] Henke B L, Gullikson E M, Davis J C 1993 At. Data Nucl. Data Tables 54 181
Google Scholar
[34] 陈田祥, 高娜, 李琳, 陈勇, 徐玉朋, 卢方军 2019 光学精密工程 27 2338
Google Scholar
Chen T X, Gao N, Li L, Chen Y, Xu Y P, Lu F J 2019 Opt. Precis. Eng. 27 2338
Google Scholar
[35] Freyberg M J, Brauninger H, Burkert W, Hartner G D, Citterio O, Mazzoleni F, Pareschi G, Spiga D, Romaine S, Gorenstein P, Ramsey B D 2005 Exp. Astron. 20 405
Google Scholar
[36] Predehl P, Andritschke R, Arefiev V, et al. 2020 Astron. Astrophys. 647 A1
Google Scholar
[37] Rukdee S, Budau B, Burwitz V 2021 Test Report-EP FXT MM ACC PANTER (MPE: PANTER) p85
[38] O’Dell S L, Elsner R F, Oosterbroek T 2010 Proc. SPIE 7732 77322V
Google Scholar
[39] Bradshaw M, Budau B, Burwitz V 2020 Test Report-EP FXT STM MA X4 Post-Thermal Test PANTER (MPE: PANTER) p67
-
图 1 (a) Wolter-I型聚焦镜光路示意图; (b) 多层嵌套结构示意图
Fig. 1. Schematic diagram of (a) optical path of Wolter-I focusing mirror and (b) multi-layer nested structure
图 3 (a) 理想镜面的反射; (b) 高频表面粗糙度误差下的XRS效应; (c) 低频面形误差下的大角度偏折
Fig. 3. (a) Ideal Reflection; (b) XRS effect under high frequency error; (c) large angle deflection under low frequency error.
图 4 (a)
$ \theta_{{\rm{i}}} = 0.7^{\circ} $ 时散射概率随RMS的变化; (b) RMS = 0.5 nm时, 不同能量下的散射角分布Fig. 4. (a) Variation of scattering probability with RMS value at
$ \theta_{{\rm{i}}} = 0.7^{\circ} $ ; (b) scattering angle distribution at different energies when RMS = 0.5 nm.
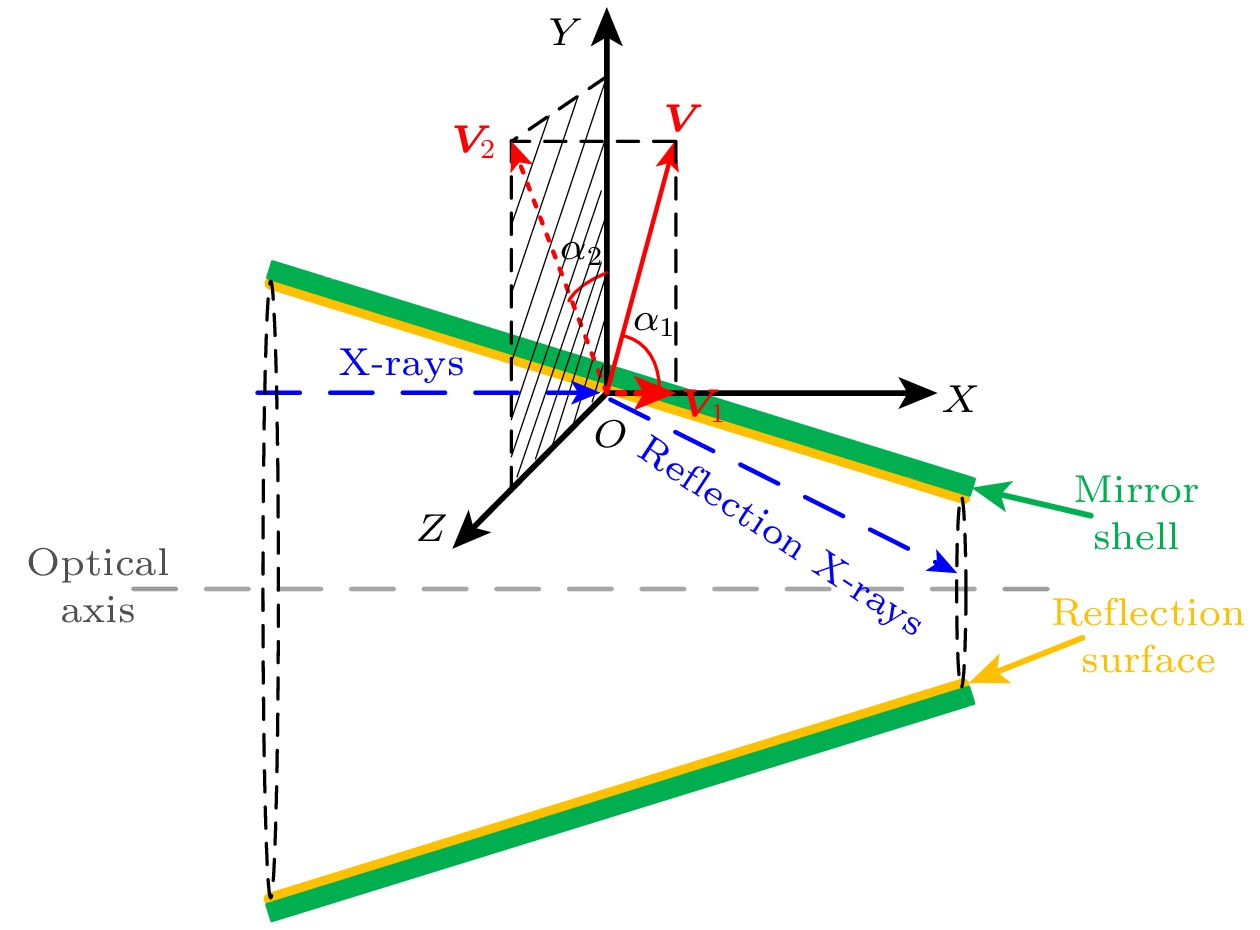
图 5 镜片二维剖面下面形误差扰动分解示意图. O点为光子在反射面上的入射点, XOY面平行于纸面, YOZ面平行于聚焦镜入射平面, X轴与光轴平行, 为方便显示, 进行了一定的夸张
Fig. 5. Decomposition diagram of surface error disturbance under two dimensional (2D) section of mirror. Point O is the incident point on the reflecting surface, the XOY and YOZ planes are parallel to the paper plane and incident plane of the mirror respectively, and the X axis is parallel to the optical axis.
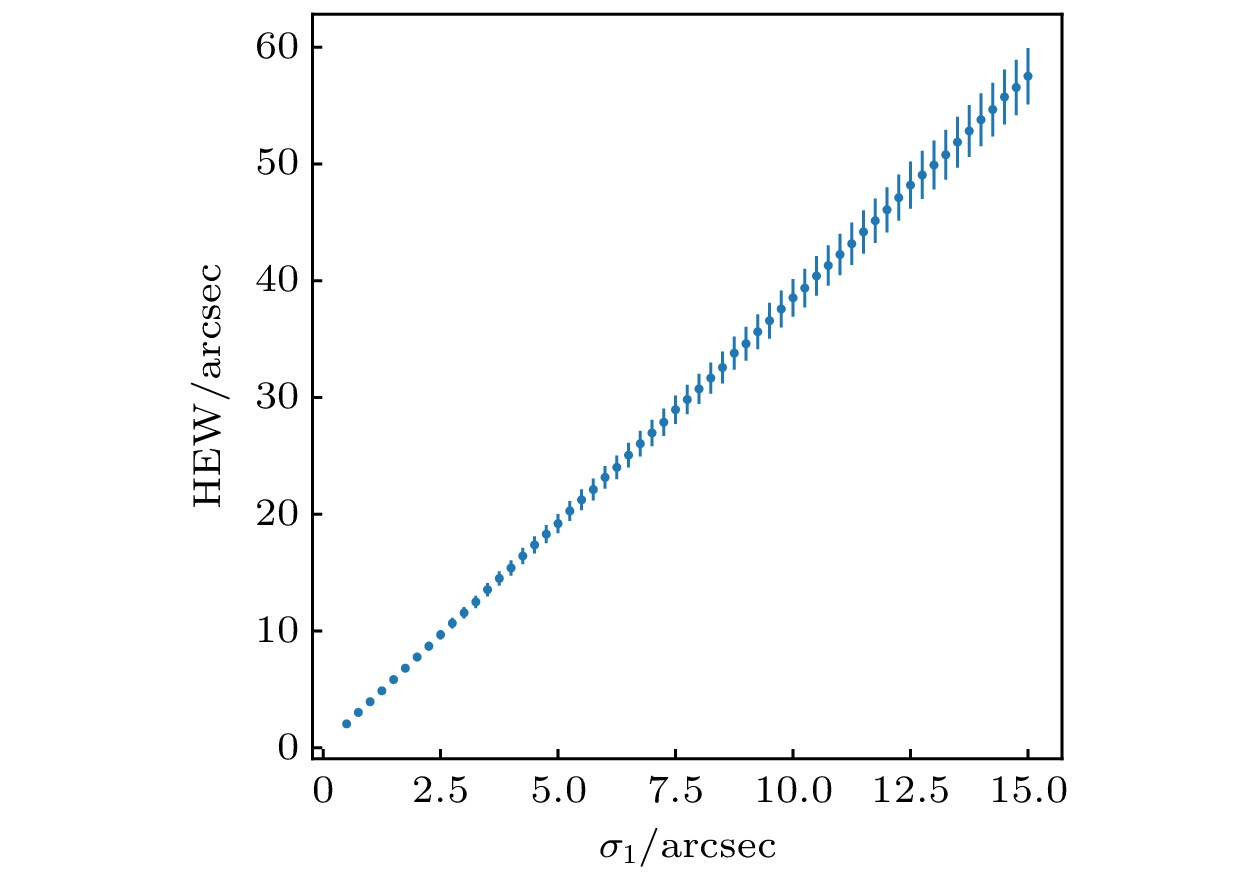
图 6 高斯模型下的扰动分量对光斑HEW的影响. 其中十字点为
${ \boldsymbol{V}_1}$ 方向扰动分量, 虚线为${\boldsymbol{V}_2}$ 方向扰动分量Fig. 6. Influence of disturbance component on spot HEW in Gaussian model. The cross point is the disturbance component in
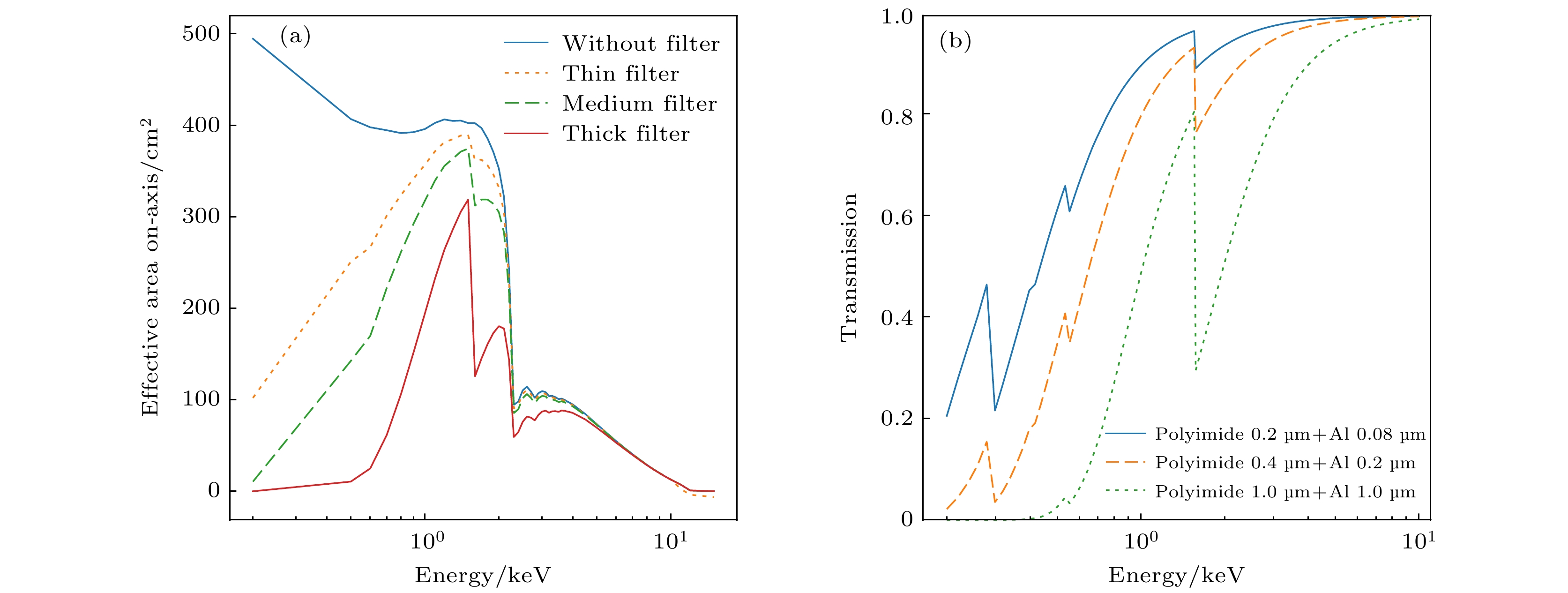
${\boldsymbol {V}_1}$ direction, and the dotted line is the disturbance component in${\boldsymbol{V}_2}$ direction
图 7 XRS对光斑PSF的影响(RMS = 0.5 nm,
$\sigma_1 = 2^{\prime \prime}, $ $ \sigma_2 = 5^{\prime \prime}$ )Fig. 7. Effect of XRS on spot PSF (RMS = 0.5 nm,
$\sigma_1 = 2^{\prime \prime}, $ $ \sigma_2 = 5^{\prime \prime}$ )
图 8 三种不同
${\boldsymbol{V}_1}$ 方向扰动$ \sigma_1 $ 下粗糙度RMS的影响 (a)对HEW 的影响; (b)对W90的影响Fig. 8. Influence of roughness RMS under three different
$ \sigma_1 $ : (a) on HEW; (b) on W90
图 9 (a) FXT聚焦镜有效面积随能量变化的模拟结果(考虑了嵌套结构支撑轮毂的遮挡效应); (b) FXT三种不同遮光膜透过率随能量变化
Fig. 9. (a) Simulation results of variation of effective area with energy of FXT focusing mirrors (support spider of multi-layer nested structure has been considered); (b) fariation of transmittance with energy of FXT’s three different filter
图 10 FXT的QM渐晕曲线实测数据拟合曲线与模拟结果对比. 对应颜色的虚线和散点分别为相同能量下的实测拟合曲线和模拟结果
Fig. 10. Fitting results of measured data and simulation results of vignetting. The dashed lines and scattered points of corresponding colors are the fitting and simulation results under the same energy respectively.
图 11 RMS = 0.5 nm时散射比例实测值与模拟值对比
Fig. 11. Comparison between measured and simulated scattering ratio when RMS = 0.5 nm
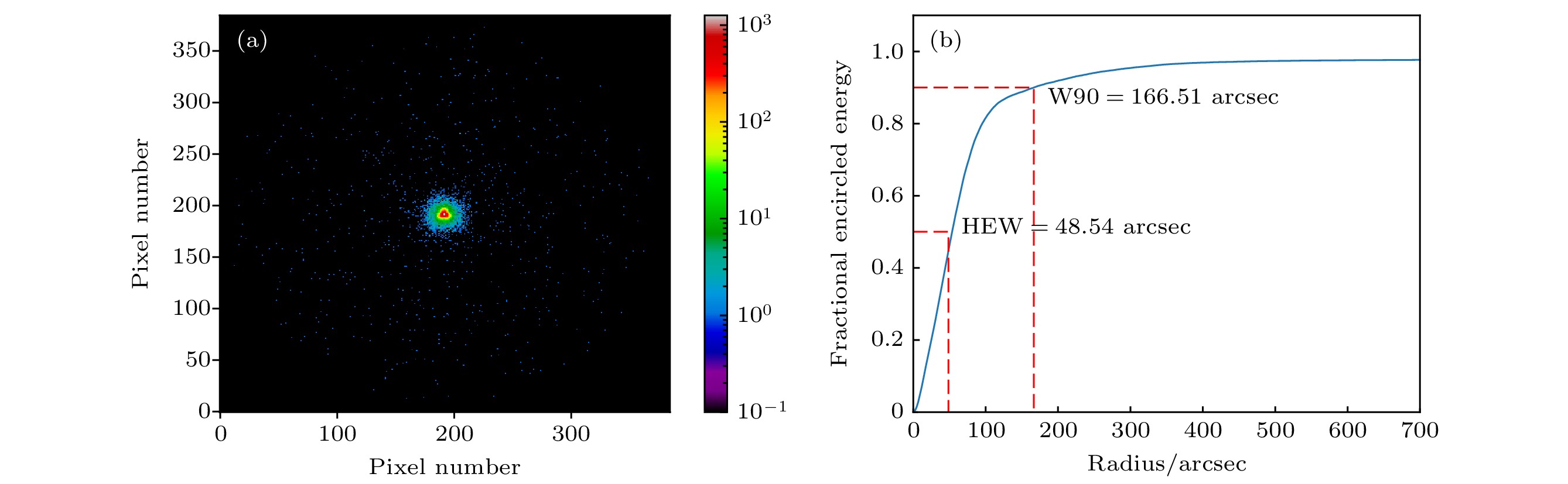
图 12 (a) STM成像结果(使用FXT焦平面探测器pnCCD, 单像素尺寸
$75 \;\text{µ} {\rm{m}}\times 75 \;\text{µ} {\rm{m}}$ , 像素数$ 384 \times 384 $ , 中间红色方形区域的放大图如上图所示); (b) STM 成像结果的EEF曲线Fig. 12. (a) Imaging and (b) EEF results of STM test (using FXT focal plane detector pnCCD, single pixel size is
$75 \;\text{µ} {\rm{m}} \times 75\;\text{µ} {\rm{m}}$ , pixel number is$ 384 \times 384 $ and the enlarged view in the middle red square area is shown in the upper in panel (a))
图 13 RMS = 0.5 nm, 光子能量为1.49 keV,
$ \sigma_2 = 5^{\prime \prime} $ 时HEW随$ \sigma_1 $ 的变化Fig. 13. Variation of HEW with
$ \sigma_1 $ when RMS = 0.5 nm, photon energy is 1.49 keV and$ \sigma_2 = 5^{\prime \prime} $ 
图 14 (a) #1镜三角形畸变成像模拟结果(焦平面探测器为pnCCD); (b)模拟光斑的EEF 曲线
Fig. 14. (a) Simulation results of triangular deformation (focal plane detector is pnCCD); (b) simulated EEF
图 15 (a) STM模拟与实测光斑的一维投影; (b) STM模拟光斑的EEF 曲线
Fig. 15. (a) One dimensional projection of STM simulated and test spot; (b) simulated and test EEF curve
表 1 FXT聚焦镜有效面积模拟结果
Table 1. Test simulations of effective area of FXT focusing mirror
Energy/keV Effective area/${\rm cm^2}$ Effective area with filter/${\rm cm^2}$ Thin Medium Thick 1.49 $401.96 \pm 3.02$ $379.94 \pm 2.89$ $356.63 \pm 2.91$ $273.22 \pm 2.53$ 8.04 $28.53 \pm 0.21$ $28.49 \pm 0.20$ $28.44 \pm 0.18$ $28.14 \pm 0.18$ 
下载: 导出CSV
Shell No. HEW/arcsec #1 $48.4 \pm 0.5$ #24—#27 $25.1 \pm 0.4$ #54 $24.4 \pm 0.4$
下载: 导出CSV
-
[1] Giacconi R, Branduardi G, Briel U, Epstein A, Fabricant D, Feigelson E, Forman W, Gorenstein P, Grindlay J, Gursky H, Harnden F R, Henry J P, Jones C, Kellogg E, Koch D, Murray S, Schreier E, Seward F, Tananbaum H, Topka K, Van Speybroeck L, Holt S S, Becker R H, Boldt E A, Serlemitsos P J, Clark G, Canizares C, Markert T, Novick R, Helfand D, Long K 1985 Astrophys. J. 230 540
Google Scholar
[2] Weisskopf M C, Tananbaum H D, Speybroeck L, O’Dell S L 2000 Proc. SPIE 4012 0277
Google Scholar
[3] Jansen F, Lumb D, Altieri B, Clavel J, Ehle M, Gabriel C, Guainazzi M, Gondoin P, Much R, Munoz R, Santos M, Schartel N, Texier D, Vacanti G 2000 Astron. Astrophys. 365 L1-L6
Google Scholar
[4] Predehl P 2017 Astron. Nachr. 338 159
Google Scholar
[5] Merloni A, Predehl P, Becker W, Bohringer H, Boller T, Brunner H, Brusa M, Dennerl K, Freyberg M, Friedrich P, Georgakakis A, Haberl F, Hasinger G, Meidinger N, Mohr J, Nandra K, Rau A, Reiprich T H, Robrade J, Salvato M, Santangelo A, Sasaki M, Schwope A, Wilms J, German eROSITA Consortium 2012 Casopis Lekaru Ceskych 99 1280
Google Scholar
[6] Li T P 2007 Nucl. Phys. B. Proc. Suppl. 166 131
Google Scholar
[7] Zhang S N, Li T P, Lu F J, et al. 2020 Sci. Chin.: Phys., Mech. Astron. 63 249502
Google Scholar
[8] Yuan W M, Zhang C, Ling Z X, Zhao D H, Wang W X, Chen Y, Lu F J, Zhang S N, Cui W 2018 Proc. SPIE 10699 1069925
Google Scholar
[9] Zhang S N, Santangelo A, Feroci M, et al. 2018 Sci. Chin.: Phys., Mech. Astron. 62 029502
Google Scholar
[10] 强鹏飞, 盛立志, 李林淼, 闫永清, 刘哲, 周晓红 2018 68 160702
Google Scholar
Qiang P F, Sheng L Z, Li L M, Yan Y Q, Liu Z, Zhou X H 2018 Acta Phys. Sin. 68 160702
Google Scholar
[11] Zhao D H, Zhang C, Yuan W M, Zhang S N, Willingale R, Ling Z X 2017 Exp. Astron. 43 267
Google Scholar
[12] Chen Y, Cui W W, Han D W, et al. 2020 Proc. SPIE 11444 114445b
Google Scholar
[13] Bernal J D 1935 Nature 136 661
Google Scholar
[14] Wolter H 1975 Ann. Phys. 10 94
[15] Zhang X Y, Shui P, Huang L W, Chen S L, Xu L H 2017 Int. J. Aerosp. Eng. 2017 8561830
Google Scholar
[16] 周庆勇, 魏子卿, 姜坤, 邓楼楼, 刘思伟, 姬剑锋, 任红飞, 王奕迪, 马高峰 2018 67 050701
Google Scholar
Zhou Q Y, Wei Z Q, Jiang K, Deng L L, Liu S W, Ji J F, Ren H F, Wang Y D, Ma G F 2018 Acta Phys. Sin. 67 050701
Google Scholar
[17] Angel J 1979 Astrophys. J. 233 364
Google Scholar
[18] Zhu Y X, Lu J B, Yang Y J, Cong M, Sheng L Z, Qiang P F, Cui W W, Zhang Z L, Wang Y S, Han D W, Li W, Wang J, Huo J, Li M S, Zhao X F, Yu N, Song Z Y, Ma J, Lv Z H, Zhao Z J, Wang H, Hou D J, Chen C, Chen T X, Yang X T, Luo L D, Lu B, Xu J J, Chen Y H, Chen Y 2021 Opt. Eng. 60 025102
Google Scholar
[19] 张星, 王娟, 张艺, 杨彦佶, 陈勇, 文健 2020 光子学报 49 0512002
Google Scholar
Zhang X, Wang J, Zhang Y, Yang Y J, Chen Y, Wen J 2020 Acta Photon. Sin. 49 0512002
Google Scholar
[20] 赵子健, 王于仨, 张留洋, 陈灿, 马佳 2019 光学精密工程 27 2331
Google Scholar
Zhao Z J, Wang Y S, Zhang L Y, Chen C, Ma J 2019 Opt. Precis. Eng. 27 2331
Google Scholar
[21] 李林森, 强鹏飞, 盛立志, 刘哲, 周晓红, 赵宝升, 张淳民 2018 67 200701
Google Scholar
Li L S, Qiang P F, Sheng L Z, Liu Z, Zhou X H, Zhao B S, Zhang C M 2018 Acta Phys. Sin. 67 200701
Google Scholar
[22] Laine R, Giralt R, Zobl R, de Korte P A, Bleeker J A M 1979 Proc. SPIE 184 181
Google Scholar
[23] Hunter W R, Michels D J, Fleetwood C M, Mangus J D, Bach B W 1980 Appl. Opt. 19 2128
Google Scholar
[24] Jin Y, Feng X, Li D, Xue J D, Wang B, Yang Y J, Ding F 2020 Optik 218 165022
Google Scholar
[25] Stover J C 2012 Optical Scattering: Measurement and analysis (SPIE) pp4–10
[26] Canestrari R, Spiga D, Pareschi G 2006 Proc. SPIE 6266 626613
Google Scholar
[27] Church L, Jenkinson H, Zavada A, Zavada J 1979 Opt. Eng. 18 182125
Google Scholar
[28] Church L, Takacs P Z 1986 Proc. SPIE 0640 126
Google Scholar
[29] Spiga D, Cusumano G, Pareschi G 2007 Proc. SPIE 6688 66880H
Google Scholar
[30] Qi L Q, Li Gang, Xu Y P, Zhang J, Yang Y J, Sheng L Z, Basso S, Campana R, Chen Y, De Rosa A, Pareschi G, Qiang P F, Santangelo A, Sironi G, Song L M, Spiga D, Tagliaferri G, Wang J, Wilms J, Zhang Y, Lu F J 2020 Nucl. Instrum. Methods Phys. Res., Sect. A 963 163702
Google Scholar
[31] Spiga D, Raimondi L, Svetina C, Zangrando M 2013 Nucl. Instrum. Methods Phys. Res., Sect. A 710 125
Google Scholar
[32] Zombeck M V, Braeuninger H, Ondrusch A, Predehl P 1981 Proc. SPIE 316 174
Google Scholar
[33] Henke B L, Gullikson E M, Davis J C 1993 At. Data Nucl. Data Tables 54 181
Google Scholar
[34] 陈田祥, 高娜, 李琳, 陈勇, 徐玉朋, 卢方军 2019 光学精密工程 27 2338
Google Scholar
Chen T X, Gao N, Li L, Chen Y, Xu Y P, Lu F J 2019 Opt. Precis. Eng. 27 2338
Google Scholar
[35] Freyberg M J, Brauninger H, Burkert W, Hartner G D, Citterio O, Mazzoleni F, Pareschi G, Spiga D, Romaine S, Gorenstein P, Ramsey B D 2005 Exp. Astron. 20 405
Google Scholar
[36] Predehl P, Andritschke R, Arefiev V, et al. 2020 Astron. Astrophys. 647 A1
Google Scholar
[37] Rukdee S, Budau B, Burwitz V 2021 Test Report-EP FXT MM ACC PANTER (MPE: PANTER) p85
[38] O’Dell S L, Elsner R F, Oosterbroek T 2010 Proc. SPIE 7732 77322V
Google Scholar
[39] Bradshaw M, Budau B, Burwitz V 2020 Test Report-EP FXT STM MA X4 Post-Thermal Test PANTER (MPE: PANTER) p67
下载:
计量
- 文章访问数: 4846
- PDF下载量: 69
- 被引次数: 0
