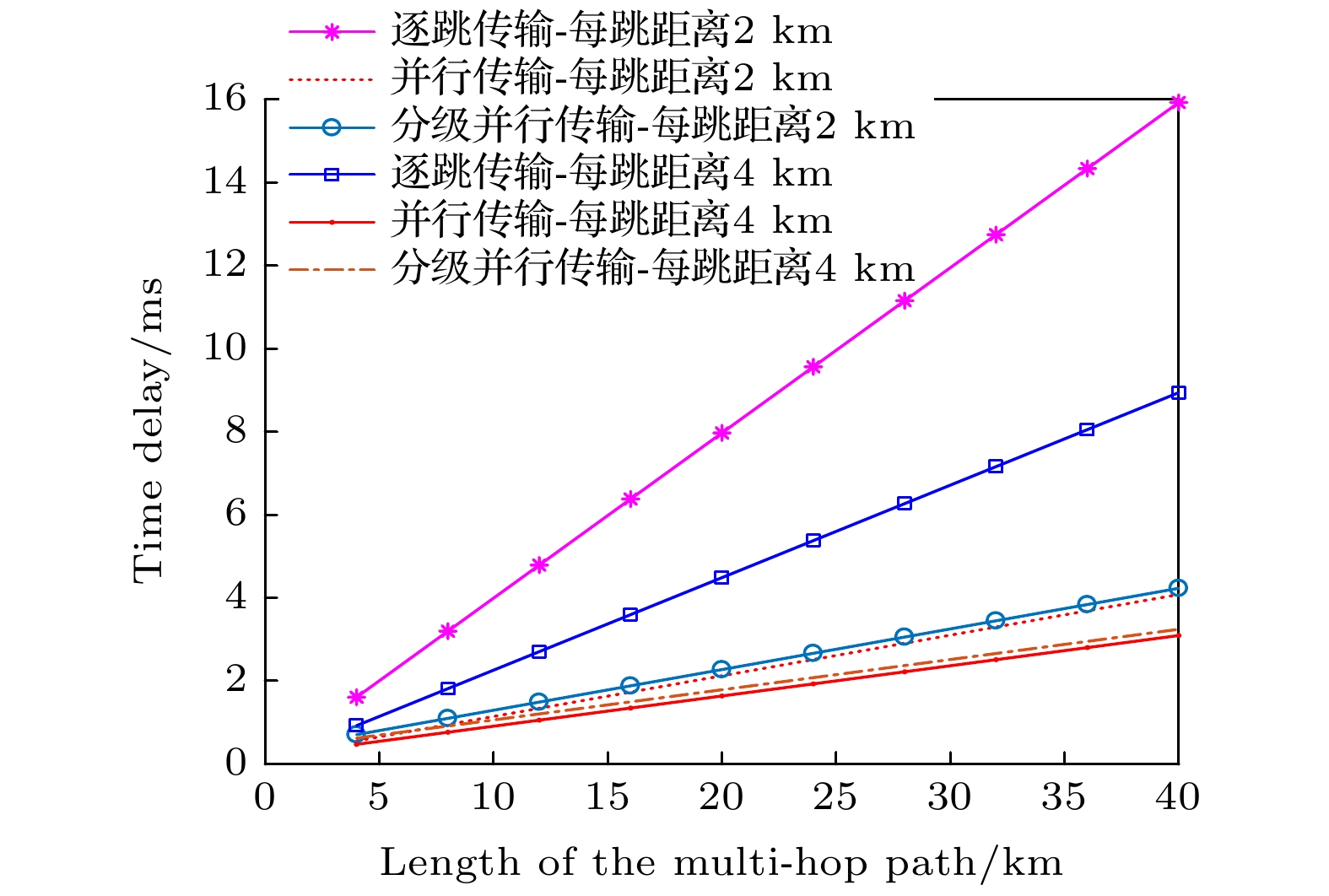
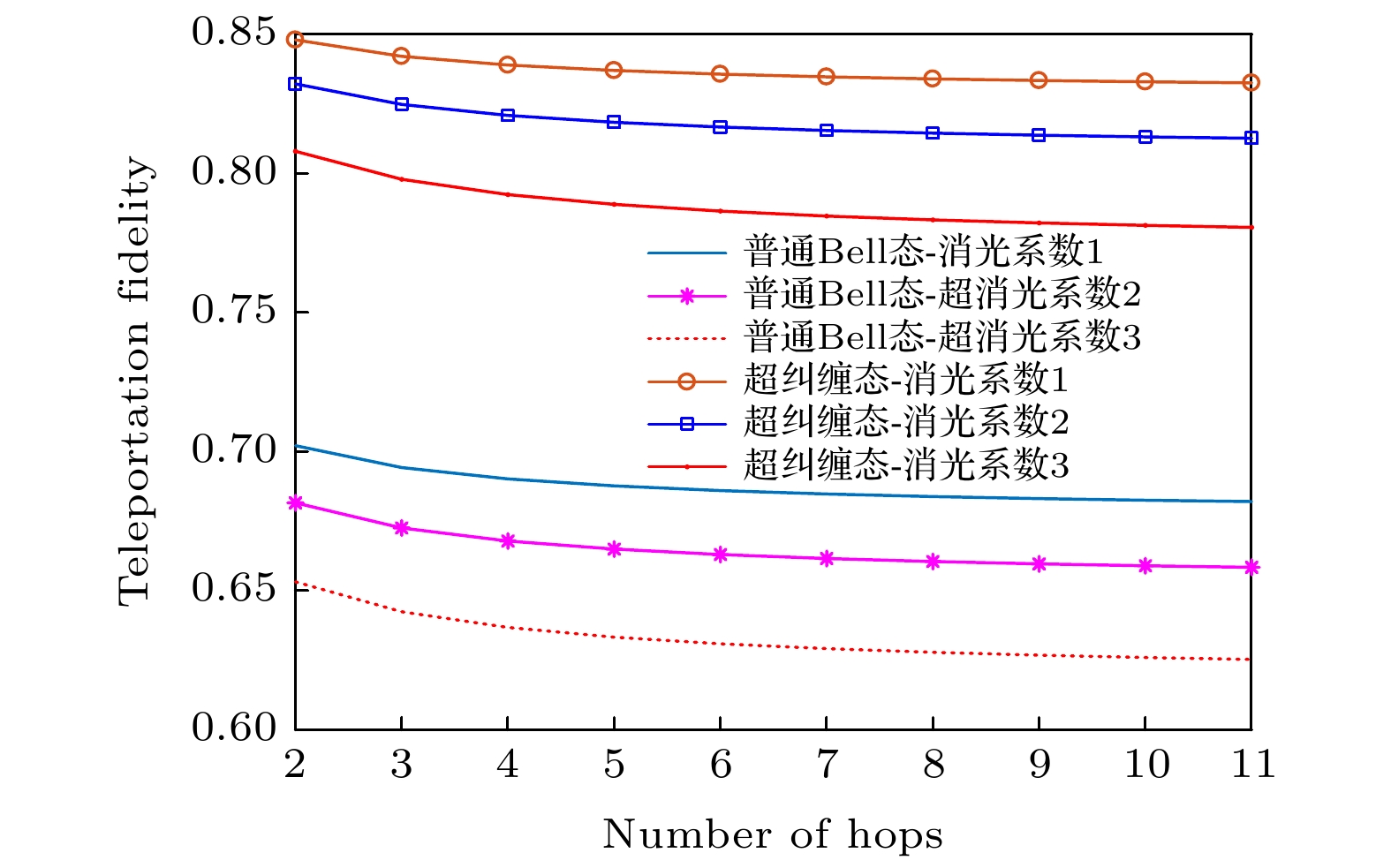
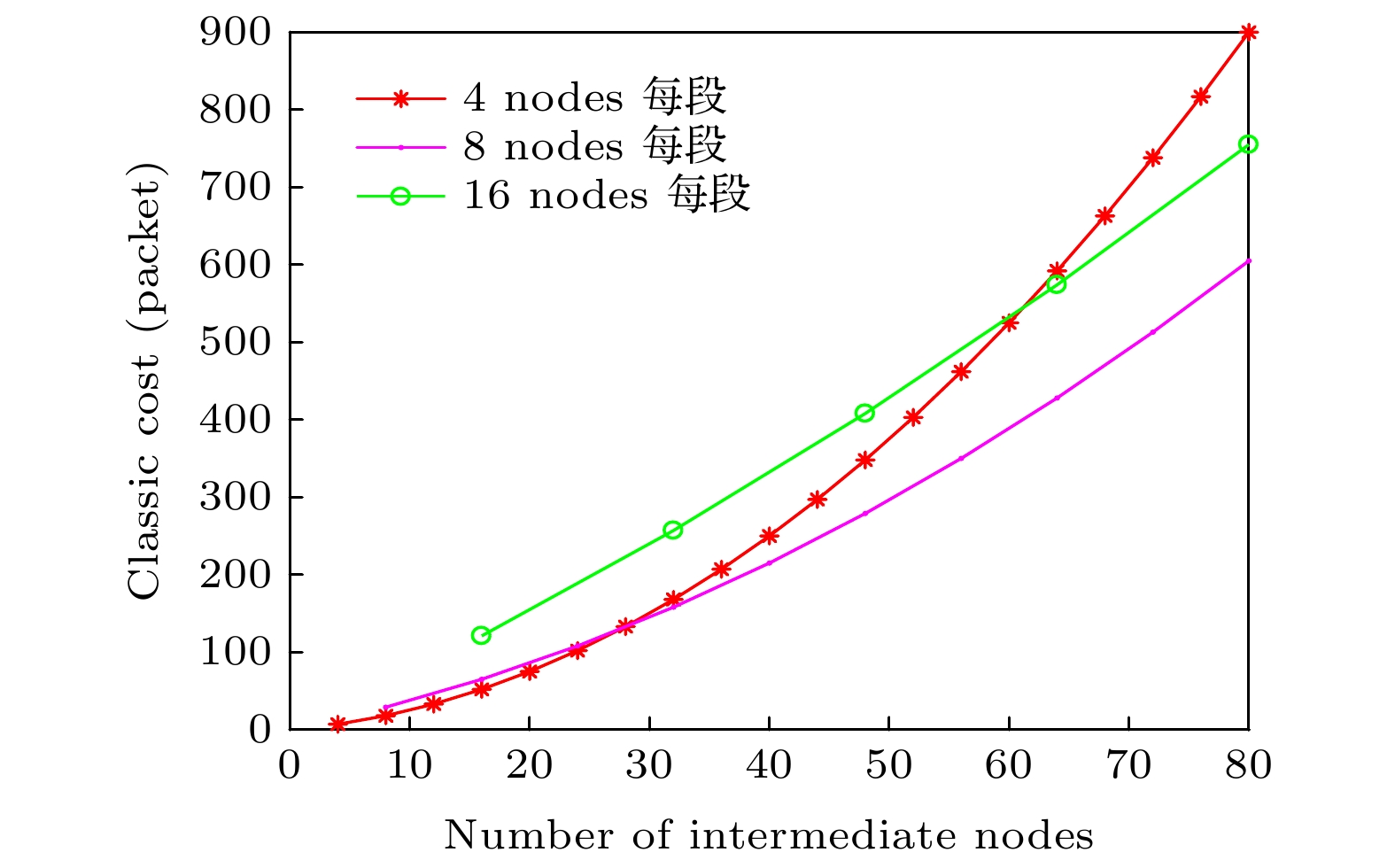
-
基于纠缠交换方法进行多跳量子信息传输,是实现远距离量子网络通信的基本方式之一. 传统的多跳量子网络通常使用单自由度极化光子纠缠态作为量子信道, 信息传输容量较低且容易受到噪声的干扰. 本文提出一种基于超纠缠的高效量子网络多跳纠缠交换方法,利用极化-空间模式两自由度的纠缠光子, 建立超纠缠量子多跳信息传输通道. 以远程超纠缠隐形传态的信道建立需求为例, 首先给出了基础的逐跳超纠缠交换方案, 为降低该方案的端到端超纠缠建立时延, 提出在中间量子节点进行同时测量的并行超纠缠交换方案. 在此基础上, 为降低并行超纠缠交换的经典信息开销, 进一步提出一种分级并行超纠缠交换方案. 理论分析及仿真结果表明该方案的纠缠建立时延接近于并行超纠缠交换方案, 但可以减少经典信息传输量, 在一定程度上实现两者的平衡. 相比传统的纠缠交换方法, 本文方案有利于解决远程超纠缠通信的需求,对未来构建更高效率的量子网络有积极意义.Entanglement swapping (ES) based multi-hop quantum information transmission is a fundamental way to realize long-distance quantum communication. However, in the conventional quantum networks, the entanglement in one degree of freedom (DOF) of photon system is usually used as a quantum channel, showing disadvantages of low capacity and susceptibility to noise. In this paper, we present an efficient multi-hop quantum hyperentanglement swapping (HES) method based on hyperentanglement, which utilizes the entangled photos in polarization and spatial-mode DOFs to establish the hyperentangled multi-hop quantum channel. Taking long-distance hyperentanglement based quantum teleportation for example, we first describe a basic hop by hop HES scheme. Then, in order to reduce the end-to-end delay of this scheme, we propose a simultaneous HES (SHES) scheme, in which the intermediate quantum nodes perform hyperentangled Bell state measurements concurrently. On the basis of this scheme, we further put forward a hierarchical SHES (HSHES) scheme that can reduce the classical information cost. Theoretical analysis and simulation results show that the end-to-end delay of HSHES is similar to that of SHES, meanwhile, the classical information cost of HSHES is much lower than that of SHES, showing a better tradeoff between the two performance metrics. Compared with the traditional ES methods, the scheme proposed in this paper is conductive to meeting the requirements for long-distance hyperentanglement based quantum communication, which has positive significance for building more efficient quantum networks in the future.
[1] Pan J W, Chen Z B, Lu Y C, Weinfurter H, Zeilinger A, Zukowsk M 2012 Rev. Mod. Phys. 84 777
Google Scholar
[2] Bennett C H, Brassard G, Crépeau C, Jozsa R, Peres A, Wootters W K 1993 Phys. Rev. Lett. 70 1895
Google Scholar
[3] 范桁 2018 67 120301
Google Scholar
Fan H 2018 Acta Phys. Sin. 67 120301
Google Scholar
[4] Luo Y H, Zhong H S, Erhard M, Wang X L, Peng C L, Krenn M, Jiang X, Li L, Liu N L, Lu C Y, Zeilinger A, Pan J W 2019 Phys. Rev. Lett. 123 070505
Google Scholar
[5] Hassanpour S, Houshmand M 2016 Quantum Inf. Process 15 905
Google Scholar
[6] Zang P, Song R, Jiang Y 2017 Chinese Journal of Quantum Electronics 34 456
[7] Paulson K G, Panigrahi P K 2019 Phys. Rev. A 100 052325
Google Scholar
[8] Shor P W, Preskill J 2000 Phys. Rev. Lett. 85 441
Google Scholar
[9] Lo H K, Curty M, Qi B 2012 Phys. Rev. Lett. 108 130503
Google Scholar
[10] Gisin N, Ribordy G, Tittel W, Zbinden H 2002 Rev. Mod. Phys. 74 145
Google Scholar
[11] Long G L, Liu X S 2002 Phys. Rev. A 65 032302
Google Scholar
[12] 曹正文, 赵光, 张爽浩, 冯晓毅, 彭进业 2016 65 230301
Google Scholar
Cao Z W, Zhao G, Zhang S H, Feng X Y, Peng J Y 2016 Acta Phys. Sin. 65 230301
Google Scholar
[13] Chen J P, Zhang C, Liu Y, Jiang C, Zhang W J, Hu X L, Guan J Y, Yu Z W, Xu H, Lin J, Li M J, Chen H, Li H, You, L X, Wang Z, Wang X B, Zhang Q, Pan J W 2020 Phys. Rev. Lett. 124 070501
Google Scholar
[14] 龙桂鲁, 潘栋 2021 信息通信技术与政策 7 7
Google Scholar
Long G L, Pan D 2021 Telecommunications Network Technology 7 7
Google Scholar
[15] Sheng Y B, Guo F G, Long G L 2010 Phys Rev. A 82 032318
Google Scholar
[16] Hong C H, Heo J, Lim J I, Yang H J 2014 Chin. Phys. B 23 090309
Google Scholar
[17] Wang X L, Cai X D, Su Z E, Cheng M C, Wu D, Li L, Liu N L, Lu C Y, Pan J W 2015 Nature 518 516
Google Scholar
[18] Xu L 2020 Modern Phys Lett. B 34 2050353
Google Scholar
[19] 彭承志, 潘建伟 2016 中国科学院院刊 31 1096
Peng C Z, Pan J W 2016 Bulletin of Chinese Academy of Sciences 31 1096
[20] Liao S K, Cai W Q 2018 Phys. Rev. Lett. 120 030501
Google Scholar
[21] 赖俊森, 赵文玉, 张海懿 2021 信息通信技术与政策 7 6
Google Scholar
Lai J S, Zhao W Y, Zhang H Y 2021 Telecommunications Network Technology 7 6
Google Scholar
[22] 聂敏, 张帆, 杨光, 张美玲, 孙爱晶, 裴昌幸 2021 70 040303
Google Scholar
Nie M, Zhang F, Yang G, Zhang M L, Sun A J, Pei C X 2021 Acta Phys. Sin. 70 040303
Google Scholar
[23] 杨光, 廉保旺, 聂敏 2015 64 010303
Google Scholar
Yang G, Lian B W, Nie M 2015 Acta Phys. Sin. 64 010303
Google Scholar
[24] 杨光, 廉保旺, 聂敏 2015 64 240304
Google Scholar
Yang G, Lian B W, Nie M 2015 Acta Phys. Sin. 64 240304
Google Scholar
[25] Briegel H J, Raussendorf R 2001 Phys. Rev. Lett. 86 910
Google Scholar
[26] Pan J W, Bouwmeester D, Weinfurter H, Zeilinger A 1998 Phys. Rev. Lett. 80 3891
Google Scholar
[27] Dotsenko I S, Korobka R 2018 Commun. Theor. Phys. 69 143
Google Scholar
[28] Li Y H, Li X L, Nie L P, Sang M H 2016 Int. J. Theor. Phys. 55 1820
Google Scholar
[29] Tao Y X, Xu J, Zhang Z C 2013 Chin. Phys. B 22 090311
Google Scholar
[30] Espoukeh P, Pedram P 2014 Int. J. Theor. Phys. 13 1789
[31] Du Z L, Li X L, Liu X J 2020 Int. J. Theor. Phys. 59 622
Google Scholar
[32] Gao X Q, Zhang Z C, Gong Y X, Sheng B, Yu X T 2017 J. Opt. Soc. Am. B-Opt. Phys. 34 142
Google Scholar
[33] Cai X F, Yu X T, Shi L H, Zhang Z C 2014 Front. Phys. 9 646
Google Scholar
[34] Xiong P Y, Yu X T, Zhang Z C, Zhan H T, Hua J Y 2017 Front. Phys. 12 1
[35] Wang K, Yu X T, Lu S L, Gong X Y 2014 Phys Rev. A 89 022329
Google Scholar
[36] Tao Y, Zhang Q, Zhang J, Yin J, Zhao Z, Zukowski M, Chen Z B, Pan J W 2005 Phys. Rev. Lett. 95 240406
Google Scholar
[37] 郭肖 2020 硕士学位论文 (西安: 西安电子科技大学 )
Guo X 2020 M. S. Dissertation (Shannxi: Xidian University) (in Chinese)
[38] 聂敏, 王超旭, 杨光, 张美玲, 孙爱晶, 裴昌幸 2021 70 030301
Google Scholar
Nie M, Wang C X, Yang G, Sun A J, Pei C X 2021 Acta Phys. Sin. 70 030301
Google Scholar
[39] 张秀再, 徐茜, 刘邦宇 2020 光学学报 40 0327001
Google Scholar
Zhang X Z, Xu Q, Liu B Y 2020 Acta Optica Sinica 40 0327001
Google Scholar
[40] Xu J, Chen X G, Xiao H W, Wang P X, Ma M 2021 Appl. Sci. 11 10869
Google Scholar
[41] Cabello A 2000 Phys. Rev. Lett. 85 5635
Google Scholar
-
图 1 极化和空间模自由度中超纠缠态产生原理
Fig. 1. Schematic diagram of the setup to generate hyperentanglement in both polarization and spatial-mode DOFs.
图 4 多级并行纠缠交换原理
Fig. 4. Schematic diagram of hierarchical simultaneous entanglement swapping.
图 6 隐形传态保真度随跳数及幅值阻尼系数的变化
Fig. 6. Teleportation fidelity versus the number of hops and the damping factor.
图 9 跳数选择与隐形传态保真度的关系
Fig. 9. Teleportation fidelity versus the choice of the number of hops.
图 11 每段节点数与经典信息开销的关系
Fig. 11. Classical costs versus number of intermediate nodes in one segment.
图 12 跳数与纠缠交换效率的关系
Fig. 12. Entanglement swapping efficiency versus the number of hops.
表 1 幺正变换表
Table 1. Unitary operations.
B和C的量子态 编码结果 A和D的量子态 Bob的幺正变换 $ \left| {{\phi ^{\text{ + }}}} \right\rangle _{P} \left| {{\phi ^{\text{ + }}}} \right\rangle _{S} $ 0000 $ \left| {{\phi ^{\text{ + }}}} \right\rangle _{P} \left| {{\phi ^{\text{ + }}}} \right\rangle _{S} $ $ {U_1} = \sigma _I^P \otimes \sigma _I^S $ $ \left| {{\phi ^{\text{ + }}}} \right\rangle _{P} \left| {{\phi ^ - }} \right\rangle _{S} $ 0001 $ \left| {{\phi ^{\text{ + }}}} \right\rangle _{P} \left| {{\phi ^ - }} \right\rangle _{S} $ $ {U_2} = \sigma _I^P \otimes \sigma _Z^S $ $ \left| {{\phi ^ - }} \right\rangle _{P} \left| {{\phi ^ + }} \right\rangle _{S} $ 0010 $ \left| {{\phi ^ - }} \right\rangle _{P} \left| {{\phi ^ + }} \right\rangle _{S} $ $ {U_3} = \sigma _Z^P \otimes \sigma _I^S $ $ \left| {{\phi ^ - }} \right\rangle _{P} \left| {{\phi ^ - }} \right\rangle _{S} $ 0011 $ \left| {{\phi ^ - }} \right\rangle _{P} \left| {{\phi ^ - }} \right\rangle _{S} $ $ {U_4} = \sigma _Z^P \otimes \sigma _Z^S $ $ \left| {{\psi ^{\text{ + }}}} \right\rangle _{P} \left| {{\phi ^{\text{ + }}}} \right\rangle _{S} $ 0100 $ \left| {{\psi ^{\text{ + }}}} \right\rangle _{P} \left| {{\phi ^{\text{ + }}}} \right\rangle _{S} $ $ {U_5} = \sigma _X^P \otimes \sigma _I^S $ $ \left| {{\psi ^{\text{ + }}}} \right\rangle _{P} \left| {{\phi ^ - }} \right\rangle _{S} $ 0101 $ \left| {{\psi ^{\text{ + }}}} \right\rangle _{P} \left| {{\phi ^ - }} \right\rangle _{S} $ $ {U_6} = \sigma _X^P \otimes \sigma _Z^S $ $ \left| {{\psi ^ - }} \right\rangle _{P} \left| {{\phi ^ + }} \right\rangle _{S} $ 0110 $ \left| {{\psi ^ - }} \right\rangle _{P} \left| {{\phi ^ + }} \right\rangle _{S} $ ${U_7} = - {{i}}\sigma _Y^P \otimes \sigma _I^S$ $ \left| {{\psi ^ - }} \right\rangle _{P} \left| {{\phi ^ - }} \right\rangle _{S} $ 0111 $ \left| {{\psi ^ - }} \right\rangle _{P} \left| {{\phi ^ - }} \right\rangle _{S} $ ${U_8} = - {{i}}\sigma _Y^P \otimes \sigma _Z^S$ $ \left| {{\phi ^{\text{ + }}}} \right\rangle _{p} \left| {{\psi ^{\text{ + }}}} \right\rangle _{S} $ 1000 $ \left| {{\phi ^{\text{ + }}}} \right\rangle _{p} \left| {{\psi ^{\text{ + }}}} \right\rangle _{S} $ $ {U_9} = \sigma _I^P \otimes \sigma _X^S $ $ \left| {{\phi ^{\text{ + }}}} \right\rangle _{p} \left| {{\psi ^ - }} \right\rangle _{S} $ 1001 $ \left| {{\phi ^{\text{ + }}}} \right\rangle _{p} \left| {{\psi ^ - }} \right\rangle _{S} $ ${U_{10} } = \sigma _I^P \otimes - {{i}}\sigma _Y^S$ $ \left| {{\phi ^ - }} \right\rangle _{p} \left| {{\psi ^ + }} \right\rangle _{S} $ 1010 $ \left| {{\phi ^ - }} \right\rangle _{p} \left| {{\psi ^ + }} \right\rangle _{S} $ $ {U_{11}} = \sigma _Z^P \otimes \sigma _X^S $ $ \left| {{\phi ^ - }} \right\rangle _{p} \left| {{\psi ^ - }} \right\rangle _{S} $ 1011 $ \left| {{\phi ^ - }} \right\rangle _{p} \left| {{\psi ^ - }} \right\rangle _{S} $ ${U_{12} } = \sigma _Z^P \otimes - {{i}}\sigma _Y^S$ $ \left| {{\psi ^ + }} \right\rangle _{P} \left| {{\psi ^ + }} \right\rangle _{S} $ 1100 $ \left| {{\psi ^ + }} \right\rangle _{P} \left| {{\psi ^ + }} \right\rangle _{S} $ $ {U_{13}} = \sigma _X^P \otimes \sigma _X^S $ $ \left| {{\psi ^ + }} \right\rangle _{P} \left| {{\psi ^ - }} \right\rangle _{S} $ 1101 $ \left| {{\psi ^ + }} \right\rangle _{P} \left| {{\psi ^ - }} \right\rangle _{S} $ ${U_{14} } = \sigma _X^P \otimes - {{i}}\sigma _Y^S$ $ \left| {{\psi ^ - }} \right\rangle _{P} \left| {{\psi ^ + }} \right\rangle _{S} $ 1110 $ \left| {{\psi ^ - }} \right\rangle _{P} \left| {{\psi ^ + }} \right\rangle _{S} $ ${U_{15} } = - {{i}}\sigma _Y^P \otimes \sigma _X^S$ $ \left| {{\psi ^ - }} \right\rangle _{P} \left| {{\psi ^ - }} \right\rangle _{S} $ 1111 $ \left| {{\psi ^ - }} \right\rangle _{P} \left| {{\psi ^ - }} \right\rangle _{S} $ ${U_{16} } = - {{i}}\sigma _Y^P \otimes - {\rm{i} }\sigma _Y^S$ 
下载: 导出CSV
表 2 多跳并行幺正变换表
Table 2. Multi-hop parallel entanglement swapping unitary operations
N1, N2, ···NN – 1 测量结果 Alice的幺正变换 $ \overline { \oplus _{i = 1}^{N - 1}{\text{MN}}_P^{i1}} \cdot \overline { \oplus _{i = 1}^{N - 1}{\text{MN}}_P^{i2}} \otimes \overline { \oplus _{i = 1}^{N - 1}{\text{MN}}_S^{i1}} \cdot \overline { \oplus _{i = 1}^{N - 1}{\text{MN}}_S^{i2}} = 1 $ $ {U_1} = \sigma _I^P \otimes \sigma _I^S $ $ \overline { \oplus _{i = 1}^{N - 1}{\text{MN}}_P^{i1}} \cdot \overline { \oplus _{i = 1}^{N - 1}{\text{MN}}_P^{i2}} \otimes \overline { \oplus _{i = 1}^{N - 1}{\text{MN}}_S^{i1}} \cdot \oplus _{i = 1}^{N - 1}{\text{MN}}_S^{i2} = 1 $ $ {U_2} = \sigma _I^P \otimes \sigma _Z^S $ $ \overline { \oplus _{i = 1}^{N - 1}{\text{MN}}_P^{i1}} \cdot \overline { \oplus _{i = 1}^{N - 1}{\text{MN}}_P^{i2}} \otimes \oplus _{i = 1}^{N - 1}{\text{MN}}_S^{i1} \cdot \overline { \oplus _{i = 1}^{N - 1}{\text{MN}}_S^{i2}} = 1 $ $ {U_3} = \sigma _I^P \otimes \sigma _X^S $ $ \overline { \oplus _{i = 1}^{N - 1}{\text{MN}}_P^{i1}} \cdot \overline { \oplus _{i = 1}^{N - 1}{\text{MN}}_P^{i2}} \otimes \oplus _{i = 1}^{N - 1}{\text{MN}}_S^{i1} \cdot \oplus _{i = 1}^{N - 1}{\text{MN}}_S^{i2} = 1 $ $ {U_4} = \sigma _I^P \otimes - i\sigma _Y^S $ $ \overline { \oplus _{i = 1}^{N - 1}{\text{MN}}_P^{i1}} \cdot \oplus _{i = 1}^{N - 1}{\text{MN}}_P^{i2} \otimes \overline { \oplus _{i = 1}^{N - 1}{\text{MN}}_S^{i1}} \cdot \overline { \oplus _{i = 1}^{N - 1}{\text{MN}}_S^{i2}} = 1 $ $ {U_5} = \sigma _I^P \otimes \sigma _I^S $ $ \overline { \oplus _{i = 1}^{N - 1}{\text{MN}}_P^{i1}} \cdot \oplus _{i = 1}^{N - 1}{\text{MN}}_P^{i2} \otimes \overline { \oplus _{i = 1}^{N - 1}{\text{MN}}_S^{i1}} \cdot \oplus _{i = 1}^{N - 1}{\text{MN}}_S^{i2} = 1 $ $ {U_6} = \sigma _Z^P \otimes \sigma _Z^S $ $ \overline { \oplus _{i = 1}^{N - 1}{\text{MN}}_P^{i1}} \cdot \oplus _{i = 1}^{N - 1}{\text{MN}}_P^{i2} \otimes \oplus _{i = 1}^{N - 1}{\text{MN}}_S^{i1} \cdot \overline { \oplus _{i = 1}^{N - 1}{\text{MN}}_S^{i2}} = 1 $ $ {U_7} = \sigma _Z^P \otimes \sigma _X^S $ $ \overline { \oplus _{i = 1}^{N - 1}{\text{MN}}_P^{i1}} \cdot \oplus _{i = 1}^{N - 1}{\text{MN}}_P^{i2} \otimes \oplus _{i = 1}^{N - 1}{\text{MN}}_S^{i1} \cdot \oplus _{i = 1}^{N - 1}{\text{MN}}_S^{i2} = 1 $ $ {U_8} = \sigma _Z^P \otimes - i\sigma _Y^S $ $ \oplus _{i = 1}^{N - 1}{\text{MN}}_P^{i1} \cdot \overline { \oplus _{i = 1}^{N - 1}{\text{MN}}_P^{i2}} \otimes \overline { \oplus _{i = 1}^{N - 1}{\text{MN}}_S^{i1}} \cdot \overline { \oplus _{i = 1}^{N - 1}{\text{MN}}_S^{i2}} = 1 $ $ {U_9} = \sigma _X^P \otimes \sigma _I^S $ $ \oplus _{i = 1}^{N - 1}{\text{MN}}_P^{i1} \cdot \overline { \oplus _{i = 1}^{N - 1}{\text{MN}}_P^{i2}} \otimes \overline { \oplus _{i = 1}^{N - 1}{\text{MN}}_S^{i1}} \cdot \oplus _{i = 1}^{N - 1}{\text{MN}}_S^{i2} = 1 $ $ {U_{10}} = \sigma _X^P \otimes \sigma _Z^S $ $ \oplus _{i = 1}^{N - 1}{\text{MN}}_P^{i1} \cdot \overline { \oplus _{i = 1}^{N - 1}{\text{MN}}_P^{i2}} \otimes \oplus _{i = 1}^{N - 1}{\text{MN}}_S^{i1} \cdot \overline { \oplus _{i = 1}^{N - 1}{\text{MN}}_S^{i2}} = 1 $ $ {U_{11}} = \sigma _X^P \otimes \sigma _X^S $ $ \oplus _{i = 1}^{N - 1}{\text{MN}}_P^{i1} \cdot \overline { \oplus _{i = 1}^{N - 1}{\text{MN}}_P^{i2}} \otimes \oplus _{i = 1}^{N - 1}{\text{MN}}_S^{i1} \cdot \oplus _{i = 1}^{N - 1}{\text{MN}}_S^{i2} = 1 $ $ {U_{12}} = \sigma _X^P \otimes - i\sigma _Y^S $ $ \oplus _{i = 1}^{N - 1}{\text{MN}}_P^{i1} \cdot \oplus _{i = 1}^{N - 1}{\text{MN}}_P^{i2} \otimes \overline { \oplus _{i = 1}^{N - 1}{\text{MN}}_S^{i1}} \cdot \overline { \oplus _{i = 1}^{N - 1}{\text{MN}}_S^{i2}} = 1 $ $ {U_{13}} = - i\sigma _Y^P \otimes \sigma _I^S $ $ \oplus _{i = 1}^{N - 1}{\text{MN}}_P^{i1} \cdot \oplus _{i = 1}^{N - 1}{\text{MN}}_P^{i2} \otimes \overline { \oplus _{i = 1}^{N - 1}{\text{MN}}_S^{i1}} \cdot \oplus _{i = 1}^{N - 1}{\text{MN}}_S^{i2} = 1 $ $ {U_{14}} = - i\sigma _Y^P \otimes \sigma _Z^S $ $ \oplus _{i = 1}^{N - 1}{\text{MN}}_P^{i1} \cdot \oplus _{i = 1}^{N - 1}{\text{MN}}_P^{i2} \otimes \oplus _{i = 1}^{N - 1}{\text{MN}}_S^{i1} \cdot \overline { \oplus _{i = 1}^{N - 1}{\text{MN}}_S^{i2}} = 1 $ $ {U_{15}} = - i\sigma _Y^P \otimes \sigma _X^S $ $ \oplus _{i = 1}^{N - 1}{\text{MN}}_P^{i1} \cdot \oplus _{i = 1}^{N - 1}{\text{MN}}_P^{i2} \otimes \oplus _{i = 1}^{N - 1}{\text{MN}}_S^{i1} \cdot \oplus _{i = 1}^{N - 1}{\text{MN}}_S^{i2} = 1 $ $ {U_{1{\text{6}}}} = - i\sigma _Y^P \otimes - i\sigma _Y^S $
下载: 导出CSV
-
[1] Pan J W, Chen Z B, Lu Y C, Weinfurter H, Zeilinger A, Zukowsk M 2012 Rev. Mod. Phys. 84 777
Google Scholar
[2] Bennett C H, Brassard G, Crépeau C, Jozsa R, Peres A, Wootters W K 1993 Phys. Rev. Lett. 70 1895
Google Scholar
[3] 范桁 2018 67 120301
Google Scholar
Fan H 2018 Acta Phys. Sin. 67 120301
Google Scholar
[4] Luo Y H, Zhong H S, Erhard M, Wang X L, Peng C L, Krenn M, Jiang X, Li L, Liu N L, Lu C Y, Zeilinger A, Pan J W 2019 Phys. Rev. Lett. 123 070505
Google Scholar
[5] Hassanpour S, Houshmand M 2016 Quantum Inf. Process 15 905
Google Scholar
[6] Zang P, Song R, Jiang Y 2017 Chinese Journal of Quantum Electronics 34 456
[7] Paulson K G, Panigrahi P K 2019 Phys. Rev. A 100 052325
Google Scholar
[8] Shor P W, Preskill J 2000 Phys. Rev. Lett. 85 441
Google Scholar
[9] Lo H K, Curty M, Qi B 2012 Phys. Rev. Lett. 108 130503
Google Scholar
[10] Gisin N, Ribordy G, Tittel W, Zbinden H 2002 Rev. Mod. Phys. 74 145
Google Scholar
[11] Long G L, Liu X S 2002 Phys. Rev. A 65 032302
Google Scholar
[12] 曹正文, 赵光, 张爽浩, 冯晓毅, 彭进业 2016 65 230301
Google Scholar
Cao Z W, Zhao G, Zhang S H, Feng X Y, Peng J Y 2016 Acta Phys. Sin. 65 230301
Google Scholar
[13] Chen J P, Zhang C, Liu Y, Jiang C, Zhang W J, Hu X L, Guan J Y, Yu Z W, Xu H, Lin J, Li M J, Chen H, Li H, You, L X, Wang Z, Wang X B, Zhang Q, Pan J W 2020 Phys. Rev. Lett. 124 070501
Google Scholar
[14] 龙桂鲁, 潘栋 2021 信息通信技术与政策 7 7
Google Scholar
Long G L, Pan D 2021 Telecommunications Network Technology 7 7
Google Scholar
[15] Sheng Y B, Guo F G, Long G L 2010 Phys Rev. A 82 032318
Google Scholar
[16] Hong C H, Heo J, Lim J I, Yang H J 2014 Chin. Phys. B 23 090309
Google Scholar
[17] Wang X L, Cai X D, Su Z E, Cheng M C, Wu D, Li L, Liu N L, Lu C Y, Pan J W 2015 Nature 518 516
Google Scholar
[18] Xu L 2020 Modern Phys Lett. B 34 2050353
Google Scholar
[19] 彭承志, 潘建伟 2016 中国科学院院刊 31 1096
Peng C Z, Pan J W 2016 Bulletin of Chinese Academy of Sciences 31 1096
[20] Liao S K, Cai W Q 2018 Phys. Rev. Lett. 120 030501
Google Scholar
[21] 赖俊森, 赵文玉, 张海懿 2021 信息通信技术与政策 7 6
Google Scholar
Lai J S, Zhao W Y, Zhang H Y 2021 Telecommunications Network Technology 7 6
Google Scholar
[22] 聂敏, 张帆, 杨光, 张美玲, 孙爱晶, 裴昌幸 2021 70 040303
Google Scholar
Nie M, Zhang F, Yang G, Zhang M L, Sun A J, Pei C X 2021 Acta Phys. Sin. 70 040303
Google Scholar
[23] 杨光, 廉保旺, 聂敏 2015 64 010303
Google Scholar
Yang G, Lian B W, Nie M 2015 Acta Phys. Sin. 64 010303
Google Scholar
[24] 杨光, 廉保旺, 聂敏 2015 64 240304
Google Scholar
Yang G, Lian B W, Nie M 2015 Acta Phys. Sin. 64 240304
Google Scholar
[25] Briegel H J, Raussendorf R 2001 Phys. Rev. Lett. 86 910
Google Scholar
[26] Pan J W, Bouwmeester D, Weinfurter H, Zeilinger A 1998 Phys. Rev. Lett. 80 3891
Google Scholar
[27] Dotsenko I S, Korobka R 2018 Commun. Theor. Phys. 69 143
Google Scholar
[28] Li Y H, Li X L, Nie L P, Sang M H 2016 Int. J. Theor. Phys. 55 1820
Google Scholar
[29] Tao Y X, Xu J, Zhang Z C 2013 Chin. Phys. B 22 090311
Google Scholar
[30] Espoukeh P, Pedram P 2014 Int. J. Theor. Phys. 13 1789
[31] Du Z L, Li X L, Liu X J 2020 Int. J. Theor. Phys. 59 622
Google Scholar
[32] Gao X Q, Zhang Z C, Gong Y X, Sheng B, Yu X T 2017 J. Opt. Soc. Am. B-Opt. Phys. 34 142
Google Scholar
[33] Cai X F, Yu X T, Shi L H, Zhang Z C 2014 Front. Phys. 9 646
Google Scholar
[34] Xiong P Y, Yu X T, Zhang Z C, Zhan H T, Hua J Y 2017 Front. Phys. 12 1
[35] Wang K, Yu X T, Lu S L, Gong X Y 2014 Phys Rev. A 89 022329
Google Scholar
[36] Tao Y, Zhang Q, Zhang J, Yin J, Zhao Z, Zukowski M, Chen Z B, Pan J W 2005 Phys. Rev. Lett. 95 240406
Google Scholar
[37] 郭肖 2020 硕士学位论文 (西安: 西安电子科技大学 )
Guo X 2020 M. S. Dissertation (Shannxi: Xidian University) (in Chinese)
[38] 聂敏, 王超旭, 杨光, 张美玲, 孙爱晶, 裴昌幸 2021 70 030301
Google Scholar
Nie M, Wang C X, Yang G, Sun A J, Pei C X 2021 Acta Phys. Sin. 70 030301
Google Scholar
[39] 张秀再, 徐茜, 刘邦宇 2020 光学学报 40 0327001
Google Scholar
Zhang X Z, Xu Q, Liu B Y 2020 Acta Optica Sinica 40 0327001
Google Scholar
[40] Xu J, Chen X G, Xiao H W, Wang P X, Ma M 2021 Appl. Sci. 11 10869
Google Scholar
[41] Cabello A 2000 Phys. Rev. Lett. 85 5635
Google Scholar
下载:
计量
- 文章访问数: 4580
- PDF下载量: 69
- 被引次数: 0
