-
基于高效的单团簇生长算法, 采用蒙特卡罗方法模拟了考虑最近邻、次近邻, 直至第五近邻格点的二维正方格子的键渗流. 计算得到了二十余种格点模型高精度的键渗流阈值, 并深入探讨了渗流阈值
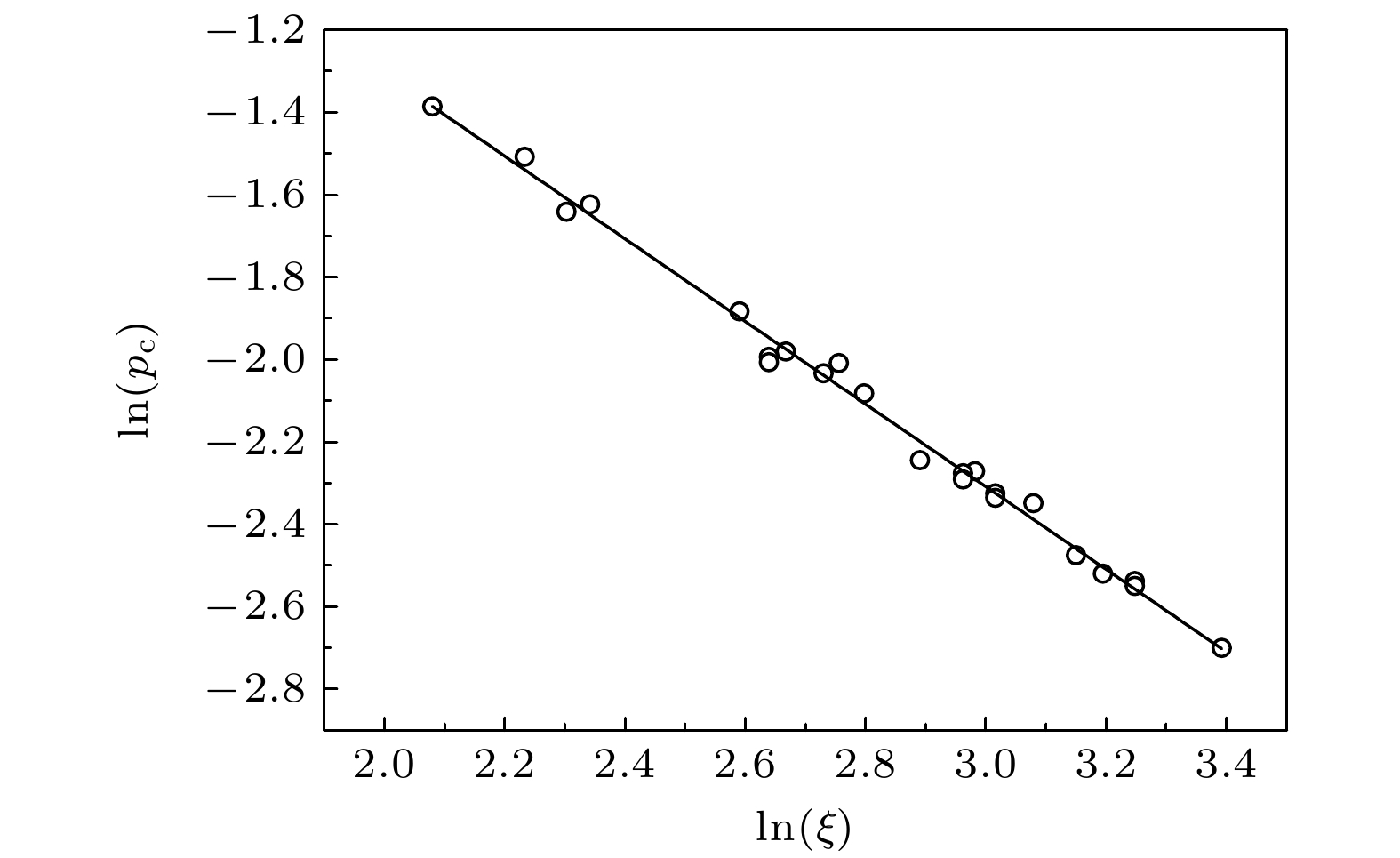
$p_{\rm c}$ 与格点结构之间的关联. 通过引入参数$\xi = \displaystyle\sum\nolimits_{i} z_{i} r_{i}^{2} / i$ (其中$z_{i}$ 和$r_{i}$ 分别为第i近邻格点的配位数及到中心格点的距离)来消除“简并”, 研究发现$p_{\rm c}$ 随ξ的变化较好地满足幂律关系$p_{\rm c} \propto \xi^{-\gamma}$ , 数值拟合得$\gamma \approx 1$ .Based on an effective single cluster growth algorithm, bond percolation on square lattice with the nearest neighbors, the next nearest neighbors, up to the 5th nearest neighbors are investigated by Monte Carlo simulations. The bond percolation thresholds for more than 20 lattices are deduced, and the correlations between percolation threshold$p_{\rm c}$ and lattice structures are discussed in depth. By introducing the index$\xi = \displaystyle\sum\nolimits_{i} z_{i} r_{i}^{2} / i$ to remove the degeneracy, it is found that the thresholds follow a power law$p_{\rm c} \propto \xi^{-\gamma}$ , with$\gamma \approx 1$ , where$z_{i}$ is the ith neighborhood coordination number, and$r_{i}$ is the distance between sites in the i-th coordination zone and the central site.-
Keywords:
- percolation /
- single cluster growth algorithm /
- Monte Carlo simulation
[1] Broadbent S R, Hammersley J M 1957 Math. Proc. Cambridge Phil. Soc. 53 629
Google Scholar
[2] Stauffer D, Aharony A 1994 Introduction to Percolation Theory (Boca Raton: CRC Press)
[3] 韩伟涛, 伊鹏 2019 68 078902
Google Scholar
Han W T, Yi P 2019 Acta Phys. Sin. 68 078902
Google Scholar
[4] 李乐, 李克非 2015 64 136402
Google Scholar
Li L, Li K F 2015 Acta Phys. Sin. 64 136402
Google Scholar
[5] 王小娟, 宋梅, 郭世泽, 杨子龙 2015 64 044502
Google Scholar
Wang X J, Song M, Guo S Z, Yang Z L 2015 Acta Phys. Sin. 64 044502
Google Scholar
[6] 李炎, 唐刚, 宋丽建, 寻之朋, 夏辉, 郝大鹏 2013 62 046401
Google Scholar
Li Y, Tang G, Song L J, Xun Z P, Xia H, Hao D P 2013 Acta Phys. Sin. 62 046401
Google Scholar
[7] Koza Z, Kondrat G, Suszczynski K 2014 J. Stat. Mech.: Th. Exp. 2014 P11005
Google Scholar
[8] Koza Z, Pola J 2016 J. Stat. Mech.: Th. Exp. 2016 103206
Google Scholar
[9] Kleinberg J M 2000 Nature 406 845
Google Scholar
[10] Sander L M, Warren C P, Sokolov I M 2003 Physica A 325 1
Google Scholar
[11] Ziff R M 2021 Physica A 568 125723
Google Scholar
[12] Domb C 1972 Biometrika 59 209
Google Scholar
[13] Dalton N W, Domb C, Sykes M F 1964 Proc. Phys. Soc. 83 496
Google Scholar
[14] Domb C, Dalton N W 1966 Proc. Phys. Soc. 89 859
Google Scholar
[15] Gouker M, Family F 1983 Phys. Rev. B 28 1449
Google Scholar
[16] Jerauld G R, Scriven L E, Davis H T 1984 J. Phys. C: Solid State 17 3429
Google Scholar
[17] Gawron T R, Cieplak M 1991 Acta Phys. Pol. A 80 461
Google Scholar
[18] d'Iribarne C, Rasigni G, Rasigni M 1995 Phys. Lett. A 209 95
Google Scholar
[19] d'Iribarne C, Rasigni M, Rasigni G 1999 J. Phys. A: Math. Gen. 32 2611
Google Scholar
[20] d'Iribarne C, Rasigni M, Rasigni G 1999 Phys. Lett. A 263 65
Google Scholar
[21] Malarz K, Galam S 2005 Phys. Rev. E 71 016125
Google Scholar
[22] Majewski M, Malarz K 2007 Acta Phys. Pol. B 38 2191
[23] Kurzawski K, Malarz K 2012 Rep. Math. Phys. 70 163
Google Scholar
[24] Malarz K 2015 Phys. Rev. E 91 043301
Google Scholar
[25] Kotwica M, Gronek P, Malarz K 2019 Int. J. Mod. Phys. C 30 1950055
Google Scholar
[26] Malarz K 2020 Chaos 30 123123
Google Scholar
[27] Ouyang Y, Deng Y J, Blote H W J 2018 Phys. Rev. E 98 062101
Google Scholar
[28] Deng Y J, Ouyang Y, Blote H W J 2019 J. Phys.: Conf. Ser. 1163 012001
Google Scholar
[29] Xun Z P, Ziff R M 2020 Phys. Rev. Research 2 013067
Google Scholar
[30] Xun Z P, Ziff R M 2020 Phys. Rev. E 102 012102
Google Scholar
[31] Galam S, Mauger A 1996 Phys. Rev. E 53 2177
Google Scholar
[32] van der Marck S C 1998 Int. J. Mod. Phys. C 9 529
Google Scholar
[33] Xun Z P, Hao D P, Ziff R M 2021 Phys. Rev. E 103 022126
Google Scholar
[34] Frei S, Perkins E 2016 Electron. J. Probab. 21 1
Google Scholar
[35] Xu W H, Wang J F, Hu H, Deng Y J 2021 Phys. Rev. E 103 022127
Google Scholar
[36] Piec S, Malarz K, Kulakowski K 2005 Int. J. Mod. Phys. C 16 1527
Google Scholar
[37] Gutman I 1994 J. Chem. Inf. Comp. Sci. 34 1087
Google Scholar
[38] Schultz H P 1989 J. Chem. Inf. Comp. Sci. 29 227
Google Scholar
[39] Malarz K 2021 Phys. Rev. E 103 052107
Google Scholar
-
图 1 正方格子中心点(“
$ \bullet $ ”)的近邻格点, 到第$ 5 $ 近邻Fig. 1. Neighbors of a central site (“
$ \bullet $ ”) on a square lattice, up to$ 5 $ th nearest neighbors.
图 2 SQ-1, 2格子键渗流在不同占据概率p下
$s^{\tau-2}P_{\geqslant s}$ 随$ s^{\sigma} $ 的变化曲线, 其中$ \tau = 187/91 $ ,$ \sigma = 36/91 $ . 插图表示主图中所示结果线性部分的斜率随占据概率p的变化关系Fig. 2. Plot of
$s^{\tau-2}P_{\geqslant s}$ vs.$ s^{\sigma} $ with$ \tau = 187/91 $ and$ \sigma = 36/91 $ for the bond percolation of the$\text{SQ-}1, 2$ lattice under different values of p. The inset indicates the slope of the linear portions of the curves shown in the main figure as a function of p.
图 3 SQ-1, 2格子键渗流在不同占据概率p下
$s^{\tau-2}P_{\geqslant s}$ 随$s^{-\varOmega}$ 的变化曲线, 其中$ \tau = 187/91 $ ,$\varOmega = 72/91$ Fig. 3. Plot of
$s^{\tau-2}P_{\geqslant s}$ vs.$s^{-\varOmega}$ with$ \tau = 187/91 $ and$ \varOmega = 72/91 $ for the bond percolation of the$\text{SQ-}1, 2$ lattice under different values of p.
表 1 含复杂近邻格点的二维正方格子的键渗流阈值
Table 1. Bond percolation thresholds of square lattice with complex neighborhoods.
格点模型 总配
位数 z标量
参数ξ键渗流阈值 $p_{\rm c}$ SQ-1, 2,
SQ-2, 58 8 0.2503683(7) $\text{SQ-}1, 3$ 8 9.33 0.2214989(9) $\text{SQ-}1, 5$ 8 10.4 0.1972557(13) $\text{SQ-}4$ 8 10 0.1937380(10) SQ-1, 2, 3,
SQ-2, 3, 512 13.33 0.1522201(9) $\text{SQ-}1, 2, 5$ 12 14.4 0.1380527(7) $\text{SQ-}1, 4$ 12 14 0.1362105(5) $\text{SQ-}2, 4$ 12 14 0.1345500(10) $\text{SQ-}1, 3, 5$ 12 15.73 0.1342972(8) $\text{SQ-}3, 4$ 12 15.33 0.1309686(14) $\text{SQ-}4, 5$ 12 16.4 0.1247135(15) $\text{SQ-}1, 2, 4$ 16 18 0.1059928(8) $\text{SQ-}1, 2, 3, 5$ 16 19.73 0.1032173(7) $\text{SQ-}1, 3, 4$ 16 19.33 0.1027026(6) $\text{SQ-}2, 3, 4$ 16 19.33 0.1011488(8) $\text{SQ-}1, 4, 5$ 16 20.4 0.0978026(14) $\text{SQ-}2, 4, 5$ 16 20.4 0.0967349(11) $\text{SQ-}3, 4, 5$ 16 21.73 0.0954613(7) $\text{SQ-}1, 2, 3, 4$ 20 23.33 0.0841507(7) $\text{SQ-}1, 2, 4, 5$ 20 24.4 0.0804649(9) $\text{SQ-}1, 3, 4, 5$ 20 25.73 0.0790839(9) $\text{SQ-}2, 3, 4, 5$ 20 25.73 0.0780764(6) $\text{SQ-}1, 2, 3, 4, 5$ 24 29.73 0.0671855(5) 
下载: 导出CSV
表 2 正方格子不同近邻格点的相关参数
Table 2. Parameters of different nearest neighbors on square lattice.
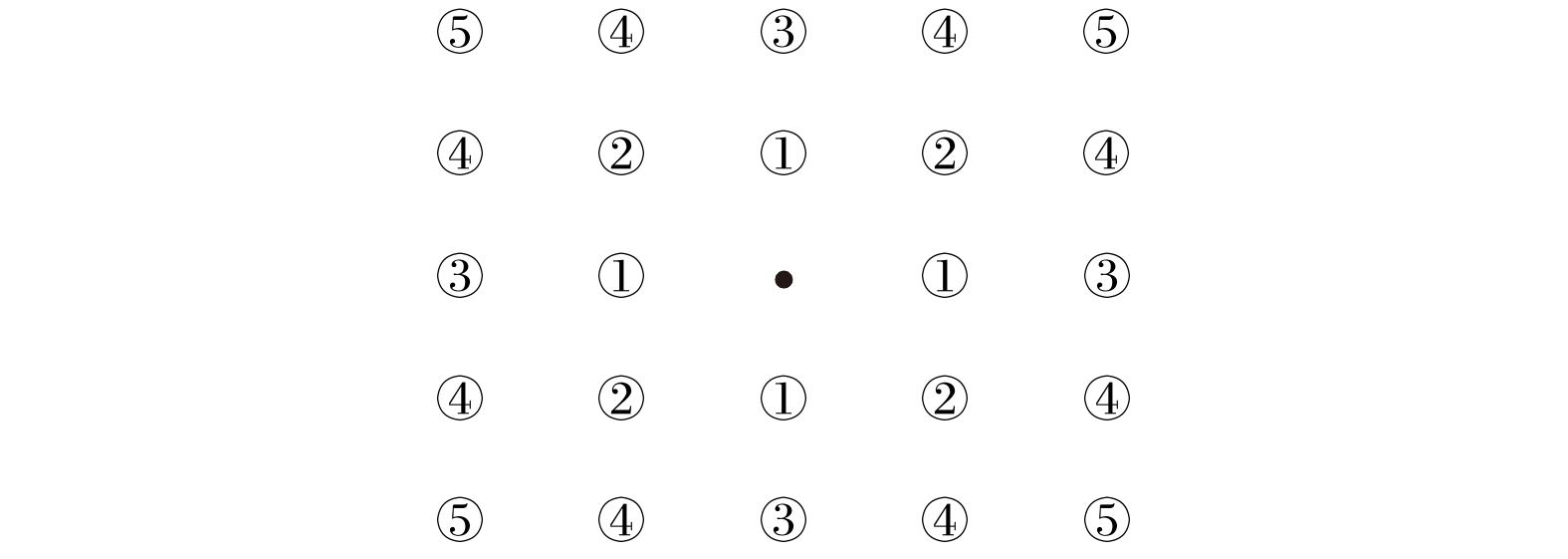
第 i 近邻 距中心格点
距离的平方 $r_{i}^{2}$第i近邻
格点数 $z_{i}$总配位数 z 1 1 4 4 2 2 4 8 3 4 4 12 4 5 8 20 5 8 4 24
下载: 导出CSV
-
[1] Broadbent S R, Hammersley J M 1957 Math. Proc. Cambridge Phil. Soc. 53 629
Google Scholar
[2] Stauffer D, Aharony A 1994 Introduction to Percolation Theory (Boca Raton: CRC Press)
[3] 韩伟涛, 伊鹏 2019 68 078902
Google Scholar
Han W T, Yi P 2019 Acta Phys. Sin. 68 078902
Google Scholar
[4] 李乐, 李克非 2015 64 136402
Google Scholar
Li L, Li K F 2015 Acta Phys. Sin. 64 136402
Google Scholar
[5] 王小娟, 宋梅, 郭世泽, 杨子龙 2015 64 044502
Google Scholar
Wang X J, Song M, Guo S Z, Yang Z L 2015 Acta Phys. Sin. 64 044502
Google Scholar
[6] 李炎, 唐刚, 宋丽建, 寻之朋, 夏辉, 郝大鹏 2013 62 046401
Google Scholar
Li Y, Tang G, Song L J, Xun Z P, Xia H, Hao D P 2013 Acta Phys. Sin. 62 046401
Google Scholar
[7] Koza Z, Kondrat G, Suszczynski K 2014 J. Stat. Mech.: Th. Exp. 2014 P11005
Google Scholar
[8] Koza Z, Pola J 2016 J. Stat. Mech.: Th. Exp. 2016 103206
Google Scholar
[9] Kleinberg J M 2000 Nature 406 845
Google Scholar
[10] Sander L M, Warren C P, Sokolov I M 2003 Physica A 325 1
Google Scholar
[11] Ziff R M 2021 Physica A 568 125723
Google Scholar
[12] Domb C 1972 Biometrika 59 209
Google Scholar
[13] Dalton N W, Domb C, Sykes M F 1964 Proc. Phys. Soc. 83 496
Google Scholar
[14] Domb C, Dalton N W 1966 Proc. Phys. Soc. 89 859
Google Scholar
[15] Gouker M, Family F 1983 Phys. Rev. B 28 1449
Google Scholar
[16] Jerauld G R, Scriven L E, Davis H T 1984 J. Phys. C: Solid State 17 3429
Google Scholar
[17] Gawron T R, Cieplak M 1991 Acta Phys. Pol. A 80 461
Google Scholar
[18] d'Iribarne C, Rasigni G, Rasigni M 1995 Phys. Lett. A 209 95
Google Scholar
[19] d'Iribarne C, Rasigni M, Rasigni G 1999 J. Phys. A: Math. Gen. 32 2611
Google Scholar
[20] d'Iribarne C, Rasigni M, Rasigni G 1999 Phys. Lett. A 263 65
Google Scholar
[21] Malarz K, Galam S 2005 Phys. Rev. E 71 016125
Google Scholar
[22] Majewski M, Malarz K 2007 Acta Phys. Pol. B 38 2191
[23] Kurzawski K, Malarz K 2012 Rep. Math. Phys. 70 163
Google Scholar
[24] Malarz K 2015 Phys. Rev. E 91 043301
Google Scholar
[25] Kotwica M, Gronek P, Malarz K 2019 Int. J. Mod. Phys. C 30 1950055
Google Scholar
[26] Malarz K 2020 Chaos 30 123123
Google Scholar
[27] Ouyang Y, Deng Y J, Blote H W J 2018 Phys. Rev. E 98 062101
Google Scholar
[28] Deng Y J, Ouyang Y, Blote H W J 2019 J. Phys.: Conf. Ser. 1163 012001
Google Scholar
[29] Xun Z P, Ziff R M 2020 Phys. Rev. Research 2 013067
Google Scholar
[30] Xun Z P, Ziff R M 2020 Phys. Rev. E 102 012102
Google Scholar
[31] Galam S, Mauger A 1996 Phys. Rev. E 53 2177
Google Scholar
[32] van der Marck S C 1998 Int. J. Mod. Phys. C 9 529
Google Scholar
[33] Xun Z P, Hao D P, Ziff R M 2021 Phys. Rev. E 103 022126
Google Scholar
[34] Frei S, Perkins E 2016 Electron. J. Probab. 21 1
Google Scholar
[35] Xu W H, Wang J F, Hu H, Deng Y J 2021 Phys. Rev. E 103 022127
Google Scholar
[36] Piec S, Malarz K, Kulakowski K 2005 Int. J. Mod. Phys. C 16 1527
Google Scholar
[37] Gutman I 1994 J. Chem. Inf. Comp. Sci. 34 1087
Google Scholar
[38] Schultz H P 1989 J. Chem. Inf. Comp. Sci. 29 227
Google Scholar
[39] Malarz K 2021 Phys. Rev. E 103 052107
Google Scholar
下载:
计量
- 文章访问数: 4013
- PDF下载量: 68
- 被引次数: 0
