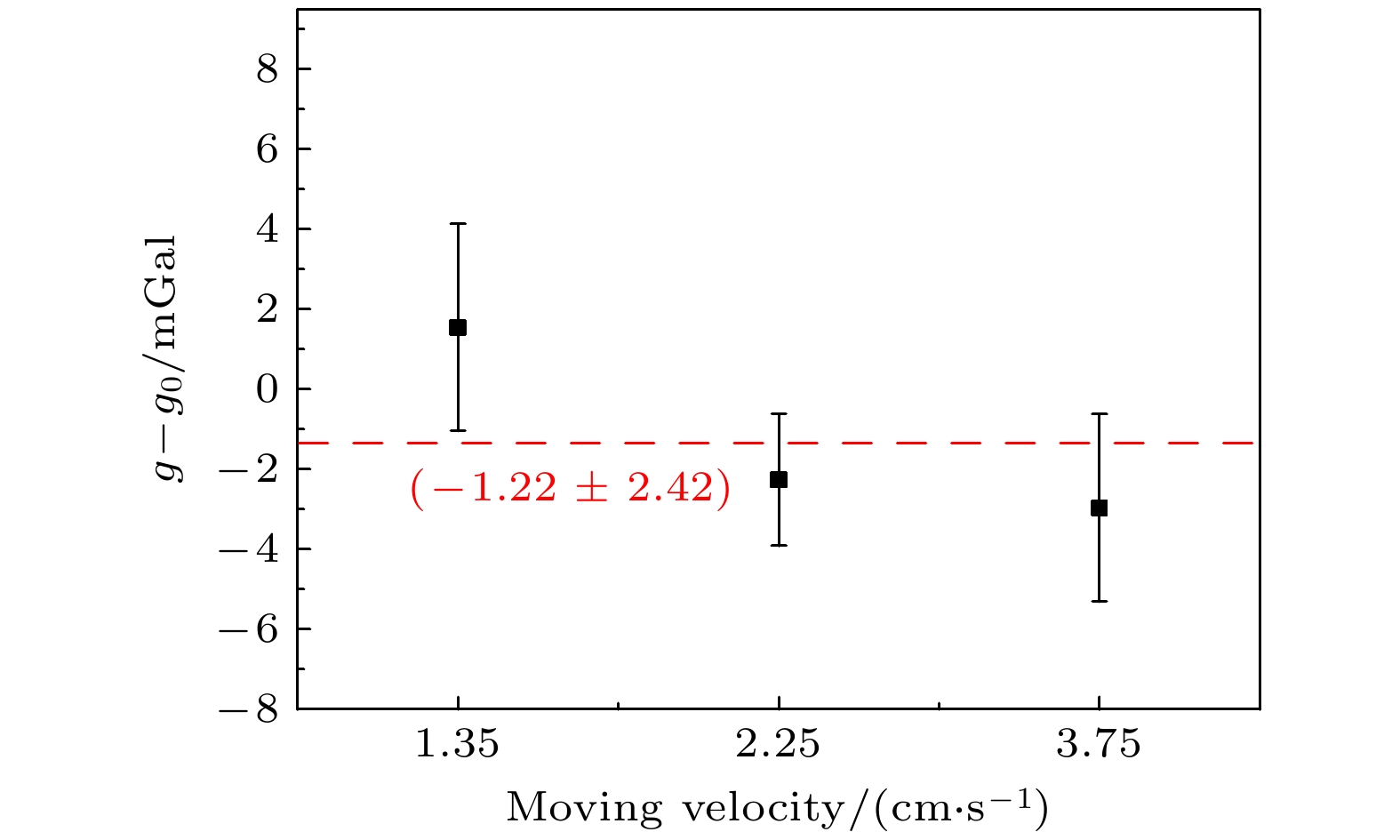
-
动态重力测量可以提高重力场的勘测效率, 对基础地质调查、资源勘探、地球物理研究等具有十分重要意义. 本文基于冷原子重力仪、惯性稳定平台和牵引动力装置搭建了一套绝对重力动态移动测量系统, 并开展了绝对重力动态测量实验. 首先测量了不同牵引速度下的垂向振动噪声功率谱, 理论分析了其对动态重力测量的影响; 其次评估了不同牵引速度对原子干涉条纹对比度和直流偏置量的影响, 分析了动态环境下的振动补偿效果; 在最大牵引速度为5.50 cm/s、最大振动幅度为0.1 m/s2的情况下, 实验上仍能基于振动补偿技术恢复原子干涉条纹. 在此基础上, 通过开展不同T下的原子干涉条纹测量, 评估了动态测量环境下的绝对重力值, 在校正完系统误差并减去绝对重力初始值后得到的测量结果为(–1.22 ± 2.42) mGal (1 Gal = 0.01 m/s2). 最后, 通过与静态环境下的绝对重力测量值进行比较, 发现两者基本吻合. 本文开展的绝对重力动态移动测量实验有望为车载动态绝对重力测量提供数据参考.Dynamic gravity measurements can improve the survey efficiency of the gravity field, and can play an important role in implementing the basic geological surveys, resource exploration, and geophysical research. Based on cold atom gravimeter, inertial stabilization platform and the movable vehicle device, a system for dynamically measuring absolute gravity is built, and the dynamic measurement experiments are carried out. Firstly, the noise power spectra of the vertical vibration are measured at different moving velocities, and the influence of such a vibration on the measurement of absolute gravity is analyzed theoretically. Besides, the influence on the contrasts and offsets of the atomic interference fringes are evaluated from different moving velocities, then the effect of vibration compensation in the dynamic measurement environment is analyzed. When the maximum moving speed is 5.50 cm/s and the maximum vibration amplitude is 0.1 m/s2, the atomic interference fringes can still be rebuilt based on the technology of vibration compensation. On this basis, the atomic interference fringes are obtained at different values of T and different moving velocities, then the absolute gravity value in the dynamic measurement environment is evaluated. After the correction of the systematic system and subtraction by the initial value of absolute gravity, the final measured result is (–1.22 ± 2.42) mGal. Finally, the experiment on the static absolute gravity is conducted, and the two values are found to be not much different from each other through comparing the static measurement data with the dynamic measurement data. The experiment of dynamic absolute gravity measurement in this paper may provide the helpful reference data for the dynamic absolute gravity measurement with moving vehicles.
[1] Bouchendira R, Clade P, Guellati Khelifa S, Nez F, Biraben F 2011 Phys. Rev. Lett 106 080801
Google Scholar
[2] Parker R H, Yu C, Zhong W, Estey B, Müller H 2018 Science 360 191
Google Scholar
[3] Rosi G, Sorrentino F, Cacciapuoti L, Prevedelli M, Tino G 2014 Nature 510 518
Google Scholar
[4] Fu Z J, Wu B, Cheng B, Zhou Y, Weng K X, Zhu D, Wang Z Y, Lin Q 2019 Metrologia 56 025001
Google Scholar
[5] Menoret V, Vermeulen P, Le Moigne N, Bonvalot S, Bouyer P, Landragin A, Desruelle B 2018 Sci. Rep 8 12300
Google Scholar
[6] Bidel Y, Carraz O, Charriere R, Cadoret M, Zahzam N, Bresson A 2013 Appl. Phys. Lett 102 144107
Google Scholar
[7] Cheiney P, Fouche L, Templier S, Napolitano F, Battelier B, Bouyer P, Barrett B 2018 Phys. Rev. Appl 10 034030
Google Scholar
[8] Zhang L, Gao W, Li Q, Li R, Yao Z, Lu S 2019 Sensors 19 222
Google Scholar
[9] Canuel B, Leduc F, Holleville D, Gauguet A, Fils J, Virdis A, Clairon A, Dimarcq N, Borde C J, Landragin A 2006 Phys. Rev. Lett 97 010402
Google Scholar
[10] Kasevich M, Chu S 1992 Appl. Phys. B 54 321
Google Scholar
[11] Yao Z W, Lu S B, Li R B, Wang K, Cao L, Wang J, Zhan M S 2016 Chin. Phys. Lett 33 083701
Google Scholar
[12] Hu Z K, Sun B L, Duan X C, Zhou M K, Chen L L, Zhan S, Zhang Q Z, Luo J 2013 Phys. Rev. A 88 043610
Google Scholar
[13] Freier C, Hauth M, Schkolnik V, Leykauf B, Schilling M, Wziontek H, Scherneck H G, Muller J, Peters A 2016 J. Phys. :Conf. Ser 723 012050
Google Scholar
[14] Le Gouet J, Mehlstaubler T E, Kim J, Merlet S, Clairon A, Landragin A, Dos Santos F P 2008 Appl. Phys. B 92 133
Google Scholar
[15] Wang S K, Zhao Y, Zhuang W, Li T C, Wu S Q, Feng J Y, Li C J 2018 Metrologia 55 360
Google Scholar
[16] Gillot P, Francis O, Landragin A, Dos Santos F P, Merlet S 2014 Metrologia 51 L15
Google Scholar
[17] 吴彬, 程冰, 付志杰, 朱栋, 周寅, 翁堪兴, 王肖隆, 林强 2018 67 190302
Google Scholar
Wu B, Cheng B, Fu Z J, Zhu D, Zhou Y, Weng K X, Wang X L, Lin Q 2018 Acta Phys. Sin 67 190302
Google Scholar
[18] Zhang X W, Zhong J Q, Tang B, Chen X, Zhu L, Huang P W, Wang J, Zhan M S 2018 Appl. Opt 57 6545
Google Scholar
[19] Wu X J, Zi F, Dudley J, Bilotta R J, Canoza P, Muller H 2017 Optica 4 1545
Google Scholar
[20] 吴彬, 程冰, 付志杰, 朱栋, 邬黎明, 王凯楠, 王河林, 王兆英, 王肖隆, 林强 2019 68 194205
Google Scholar
Wu B, Cheng B, Fu Z J, Zhu D, Wu L M, Wang K N, Wang H L, Wang Z Y, Wang X L, Lin Q 2019 Acta Phys. Sin 68 194205
Google Scholar
[21] Fu Z J, Wang Q Y, Wang Z Y, Wu B, Cheng B, Lin Q 2019 Chin. Opt. Lett 17 011204
Google Scholar
[22] Huang P W, Tang B, Chen X, Zhong J Q, Xiong Z Y, Zhou L, Wang J, Zhan M S 2019 Metrologia 56 045012
Google Scholar
[23] Wu X J, Pagel Z, Malek B S, Nguyen T H, Zi F, Scheirer D S, Muller H 2019 Sci. Adv 5 eaax0800
Google Scholar
[24] 吴彬, 周寅, 程冰, 朱栋, 王凯楠, 朱欣欣, 陈佩军, 翁堪兴, 杨秋海, 林佳宏, 张凯军, 王河林, 林强 2020 69 060302
Google Scholar
Wu B, Zhou Y, Cheng B, Zhu D, Wang K N, Zhu X X, Chen P J, Weng K X, Yang Q H, Lin J H, Zhang K J, Wang H L, Lin Q 2020 Acta Phys. Sin 69 060302
Google Scholar
[25] Barrett B, Antoni-Micollier L, Chichet L, Battelier B, Lévèque T, Landragin A, Bouyer P 2016 Nat. Commun 7 1
[26] Geiger R, Ménoret V, Stern G, Zahzam N, Cheinet P, Battelier B, Villing A, Moron F, Lours M, Bidel Y, Bresson A, Landragin A, Bouyer P 2011 Nat. Commun 2 474
Google Scholar
[27] Mahadeswaraswamy C 2009 Atom Interferometric Gravity Gradiometer: Disturbance Compensation and Mobile Gradiometry (California: Stanford University Press).
[28] Bidel Y, Zahzam N, Blanchard C, Bonnin A, Cadoret M, Bresson A, Rouxel D, Lequentrec-Lalancette M F 2018 Nat. Commun 9 9
Google Scholar
[29] Bidel Y, Zahzam N, Bresson A, Blanchard C, Cadoret M, Olesen A V, Forsberg R 2020 J. Geodesy 94 2
Google Scholar
[30] Peters A, Chung K Y, Chu S 1999 Nature 400 849
Google Scholar
[31] Peters A, Chung K Y, Chu S 2001 Metrologia 38 25
Google Scholar
[32] 程冰, 周寅, 陈佩军, 张凯军, 朱栋, 王凯楠, 翁堪兴, 王河林, 彭树萍, 王肖隆, 吴彬, 林强 2021 70 040304
Google Scholar
Cheng B, Zhou Y, Chen P J, Zhang K J, Zhu D, Wang K N, Weng K X, Wang H L, Peng S P, Wang X L, Wu B, Lin Q 2021 Acta Phys. Sin 70 040304
Google Scholar
-
图 1 动态绝对重力测量的原理示意图
Fig. 1. The schematic diagram of dynamic measurement of the absolute gravity.
图 2 动态迭代条纹拟合算法的原理示意图
Fig. 2. The schematic diagram of iterative fitting algorithm of the dynamic fringes.
图 3 绝对重力动态测量系统示意图和实物图 (a) 实验装置示意图; (b) 实验装置实物图; (c) 20 h中的温湿度统计曲线
Fig. 3. The diagram and photo of the system for dynamic measurement of the absolute gravity: (a) The diagram of the experimental system; (b) the photo of the experimental apparatus; (c) the curve of temperature and humidity in 20 h.
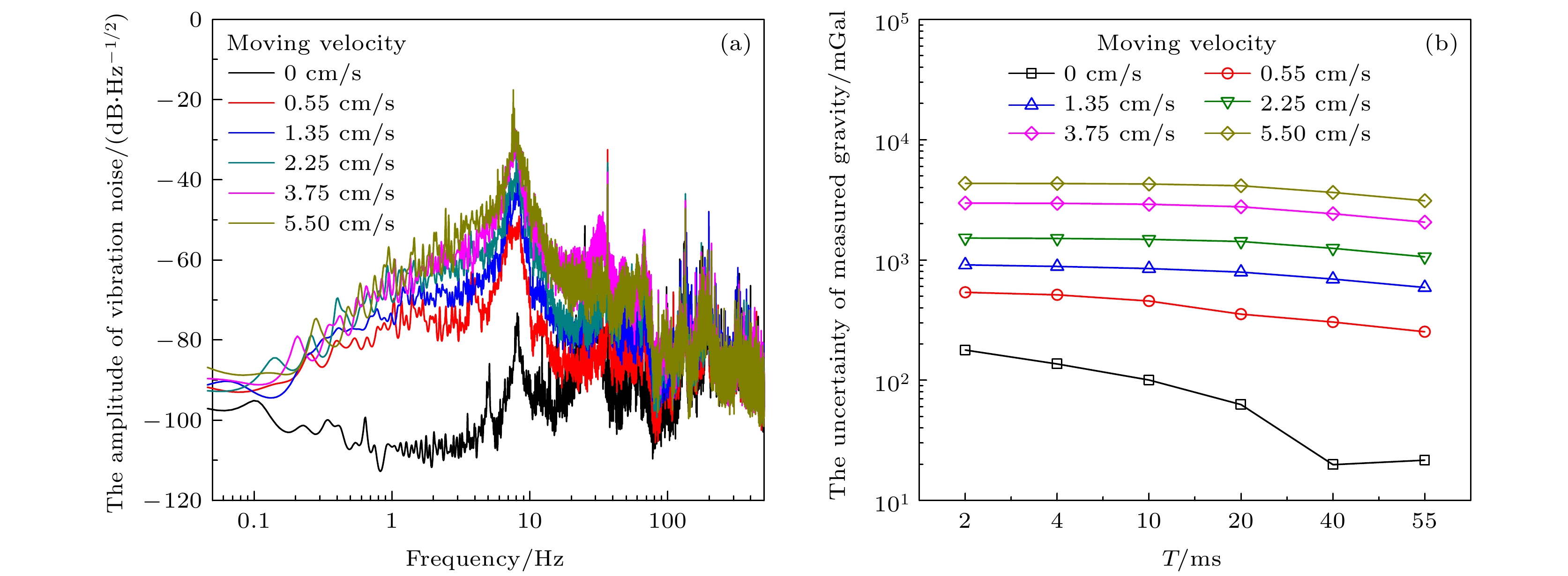
图 4 垂向振动噪声对动态重力测量的影响 (a) 静止与运动状态下垂向振动加速度的噪声功率谱; (b) 垂向振动噪声引起的重力测量不确定度
Fig. 4. The influence of vertical vibration noise on the dynamic measurement of the absolute gravity: (a) The power density spectra of vertical vibration noise in the case of static and dynamic environment; (b) the measurement uncertainty resulted from the noise of vertical vibration.
图 5 不同牵引速度下的原子干涉条纹恢复及其正弦拟合结果(T = 4 ms)
Fig. 5. The results of the recovering and fitting of the atomic interference fringes with the different moving speeds (T = 4 ms).
图 6 动态测量环境下下原子干涉条纹对比度与直流偏置量变化 (a) 原子干涉条纹对比度随牵引速度的变化曲线; (b) 原子干涉条纹直流偏置量随牵引速度的变化曲线
Fig. 6. The changes of the contrast and offset of atomic interference fringes in the case of dynamic measurement environment: (a) The changing curve of the contrast of atomic interference fringes with the moving velocity; (b)the changing curve of the offset of atomic interference fringes with the moving velocity.
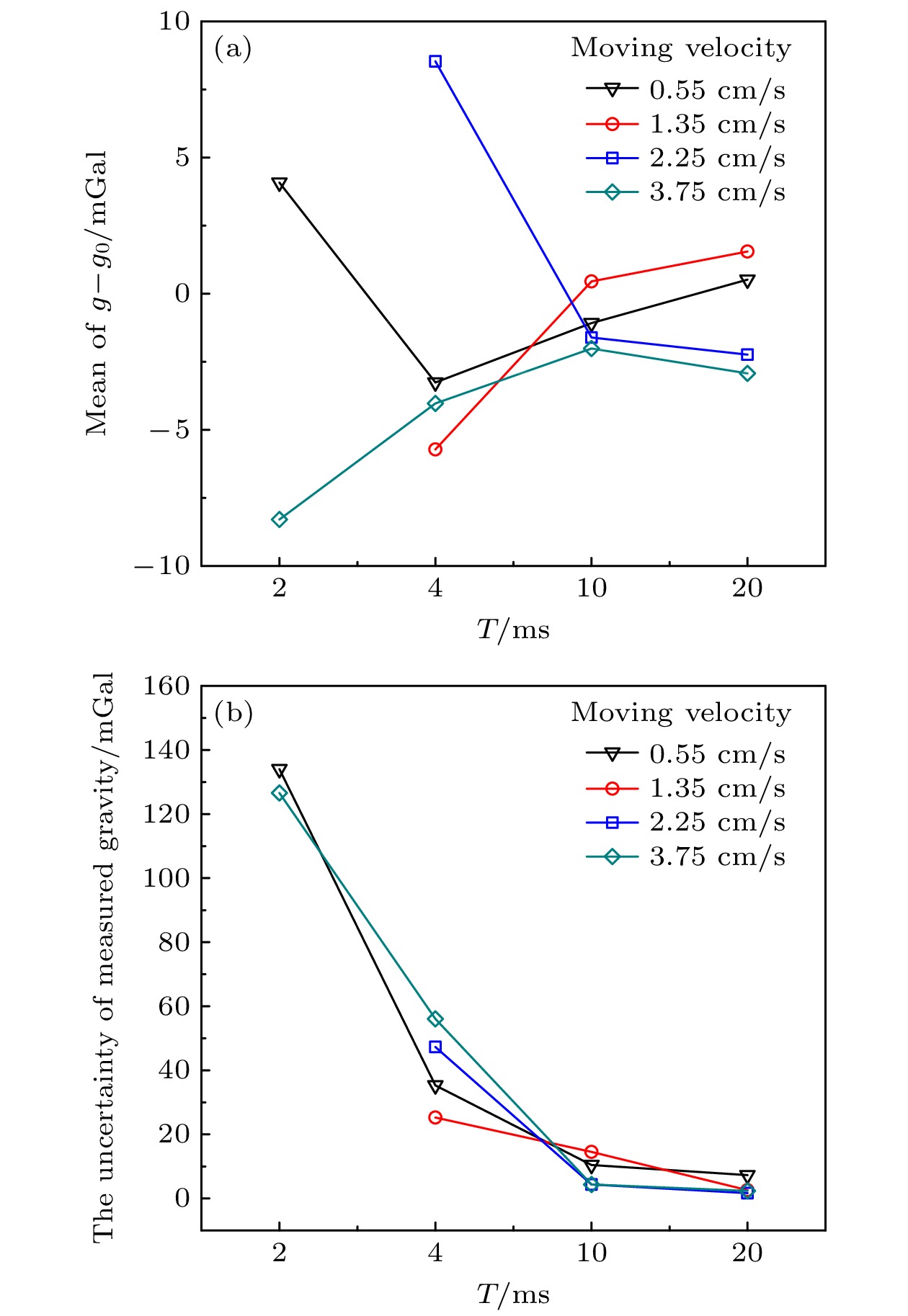
图 7 不同牵引速度、不同T下测量到的绝对重力值均值及其不确定度分析 (a) 绝对重力值的均值数据; (b) 绝对重力值的不确定度数据
Fig. 7. Analysis of the mean values and uncertainties of the absolute gravity measurement at the different velocities and different T: (a) The data of mean value of the absolute gravity measurement; (b) the uncertainties of the absolute gravity measurement.
图 8 修正完科里奥利效应后的动态绝对重力测量结果(T = 20 ms)
Fig. 8. The final experimental results of the dynamic absolute gravity measurement after the correction of the Coriolis effect (T = 20 ms).
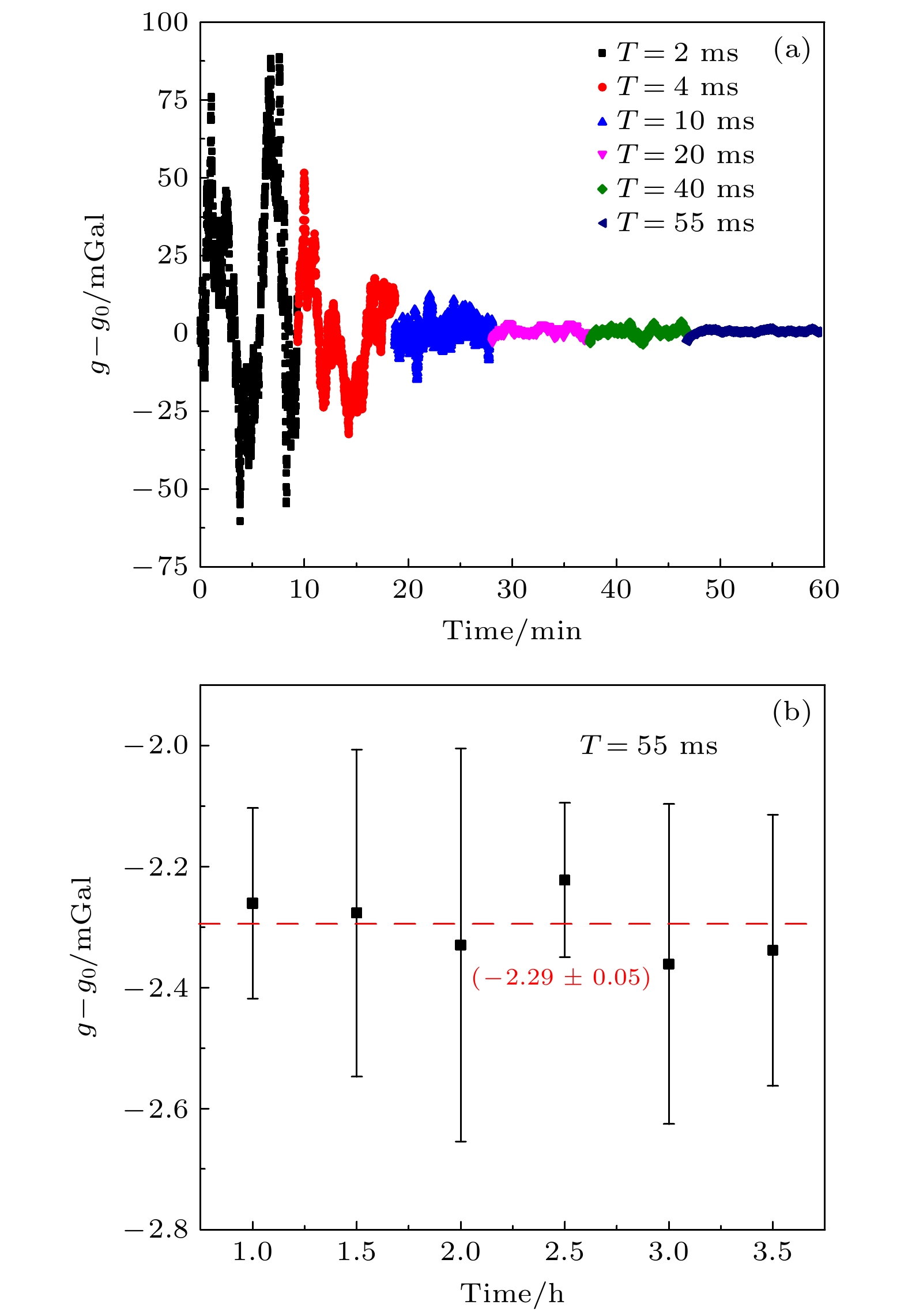
图 9 静态环境下的高精度绝对重力值评估 (a) 静态下不同T的绝对重力测量结果; (b) T = 55 ms长时间静态绝对重力测量结果
Fig. 9. The accurate evaluation of the absolute gravity in the case of static gravity measurement: (a) Absolute gravity measurements of different T at static state; (b) static absolute gravimetric measurements of T = 55 ms for a long time.
表 1 由科里奥利力效应引起的重力值修正
Table 1. The systematic corrections caused by the Coriolis effect.
Moving
velocity/(cm·s–1)0.55 1.35 2.25 3.75 $ \Delta g $/mGal 0.0006 0.0024 0.0250 0.0400 
下载: 导出CSV
表 2 车间静止测量分组重力值
Table 2. The measured gravity value in the quiet place of a workshop.
时间/h 重力均值/mGal 1.0 –2.26 1.5 –2.27 2.0 –2.31 2.5 –2.22 3.0 –2.35 3.5 –2.33
下载: 导出CSV
表 3 车间静止下的B类不确定度表
Table 3. The uncertainties of type B in case of static measurement in the workshop.
项目 修正量/μGal 不确定度/μGal 科里奥利力 –3.0 0.2 双光子光移效应 –43.2 4.0 重力梯度 –9.0 0.1 激光波长 –5.5 1.1 参考频率 0.0 2.0 射频相移 0.0 2.0 自引力效应 –2.7 0.1 其他修正量 0.0 4.0 合成结果 –63.4 13.5
下载: 导出CSV
-
[1] Bouchendira R, Clade P, Guellati Khelifa S, Nez F, Biraben F 2011 Phys. Rev. Lett 106 080801
Google Scholar
[2] Parker R H, Yu C, Zhong W, Estey B, Müller H 2018 Science 360 191
Google Scholar
[3] Rosi G, Sorrentino F, Cacciapuoti L, Prevedelli M, Tino G 2014 Nature 510 518
Google Scholar
[4] Fu Z J, Wu B, Cheng B, Zhou Y, Weng K X, Zhu D, Wang Z Y, Lin Q 2019 Metrologia 56 025001
Google Scholar
[5] Menoret V, Vermeulen P, Le Moigne N, Bonvalot S, Bouyer P, Landragin A, Desruelle B 2018 Sci. Rep 8 12300
Google Scholar
[6] Bidel Y, Carraz O, Charriere R, Cadoret M, Zahzam N, Bresson A 2013 Appl. Phys. Lett 102 144107
Google Scholar
[7] Cheiney P, Fouche L, Templier S, Napolitano F, Battelier B, Bouyer P, Barrett B 2018 Phys. Rev. Appl 10 034030
Google Scholar
[8] Zhang L, Gao W, Li Q, Li R, Yao Z, Lu S 2019 Sensors 19 222
Google Scholar
[9] Canuel B, Leduc F, Holleville D, Gauguet A, Fils J, Virdis A, Clairon A, Dimarcq N, Borde C J, Landragin A 2006 Phys. Rev. Lett 97 010402
Google Scholar
[10] Kasevich M, Chu S 1992 Appl. Phys. B 54 321
Google Scholar
[11] Yao Z W, Lu S B, Li R B, Wang K, Cao L, Wang J, Zhan M S 2016 Chin. Phys. Lett 33 083701
Google Scholar
[12] Hu Z K, Sun B L, Duan X C, Zhou M K, Chen L L, Zhan S, Zhang Q Z, Luo J 2013 Phys. Rev. A 88 043610
Google Scholar
[13] Freier C, Hauth M, Schkolnik V, Leykauf B, Schilling M, Wziontek H, Scherneck H G, Muller J, Peters A 2016 J. Phys. :Conf. Ser 723 012050
Google Scholar
[14] Le Gouet J, Mehlstaubler T E, Kim J, Merlet S, Clairon A, Landragin A, Dos Santos F P 2008 Appl. Phys. B 92 133
Google Scholar
[15] Wang S K, Zhao Y, Zhuang W, Li T C, Wu S Q, Feng J Y, Li C J 2018 Metrologia 55 360
Google Scholar
[16] Gillot P, Francis O, Landragin A, Dos Santos F P, Merlet S 2014 Metrologia 51 L15
Google Scholar
[17] 吴彬, 程冰, 付志杰, 朱栋, 周寅, 翁堪兴, 王肖隆, 林强 2018 67 190302
Google Scholar
Wu B, Cheng B, Fu Z J, Zhu D, Zhou Y, Weng K X, Wang X L, Lin Q 2018 Acta Phys. Sin 67 190302
Google Scholar
[18] Zhang X W, Zhong J Q, Tang B, Chen X, Zhu L, Huang P W, Wang J, Zhan M S 2018 Appl. Opt 57 6545
Google Scholar
[19] Wu X J, Zi F, Dudley J, Bilotta R J, Canoza P, Muller H 2017 Optica 4 1545
Google Scholar
[20] 吴彬, 程冰, 付志杰, 朱栋, 邬黎明, 王凯楠, 王河林, 王兆英, 王肖隆, 林强 2019 68 194205
Google Scholar
Wu B, Cheng B, Fu Z J, Zhu D, Wu L M, Wang K N, Wang H L, Wang Z Y, Wang X L, Lin Q 2019 Acta Phys. Sin 68 194205
Google Scholar
[21] Fu Z J, Wang Q Y, Wang Z Y, Wu B, Cheng B, Lin Q 2019 Chin. Opt. Lett 17 011204
Google Scholar
[22] Huang P W, Tang B, Chen X, Zhong J Q, Xiong Z Y, Zhou L, Wang J, Zhan M S 2019 Metrologia 56 045012
Google Scholar
[23] Wu X J, Pagel Z, Malek B S, Nguyen T H, Zi F, Scheirer D S, Muller H 2019 Sci. Adv 5 eaax0800
Google Scholar
[24] 吴彬, 周寅, 程冰, 朱栋, 王凯楠, 朱欣欣, 陈佩军, 翁堪兴, 杨秋海, 林佳宏, 张凯军, 王河林, 林强 2020 69 060302
Google Scholar
Wu B, Zhou Y, Cheng B, Zhu D, Wang K N, Zhu X X, Chen P J, Weng K X, Yang Q H, Lin J H, Zhang K J, Wang H L, Lin Q 2020 Acta Phys. Sin 69 060302
Google Scholar
[25] Barrett B, Antoni-Micollier L, Chichet L, Battelier B, Lévèque T, Landragin A, Bouyer P 2016 Nat. Commun 7 1
[26] Geiger R, Ménoret V, Stern G, Zahzam N, Cheinet P, Battelier B, Villing A, Moron F, Lours M, Bidel Y, Bresson A, Landragin A, Bouyer P 2011 Nat. Commun 2 474
Google Scholar
[27] Mahadeswaraswamy C 2009 Atom Interferometric Gravity Gradiometer: Disturbance Compensation and Mobile Gradiometry (California: Stanford University Press).
[28] Bidel Y, Zahzam N, Blanchard C, Bonnin A, Cadoret M, Bresson A, Rouxel D, Lequentrec-Lalancette M F 2018 Nat. Commun 9 9
Google Scholar
[29] Bidel Y, Zahzam N, Bresson A, Blanchard C, Cadoret M, Olesen A V, Forsberg R 2020 J. Geodesy 94 2
Google Scholar
[30] Peters A, Chung K Y, Chu S 1999 Nature 400 849
Google Scholar
[31] Peters A, Chung K Y, Chu S 2001 Metrologia 38 25
Google Scholar
[32] 程冰, 周寅, 陈佩军, 张凯军, 朱栋, 王凯楠, 翁堪兴, 王河林, 彭树萍, 王肖隆, 吴彬, 林强 2021 70 040304
Google Scholar
Cheng B, Zhou Y, Chen P J, Zhang K J, Zhu D, Wang K N, Weng K X, Wang H L, Peng S P, Wang X L, Wu B, Lin Q 2021 Acta Phys. Sin 70 040304
Google Scholar
下载:
计量
- 文章访问数: 5881
- PDF下载量: 173
- 被引次数: 0
