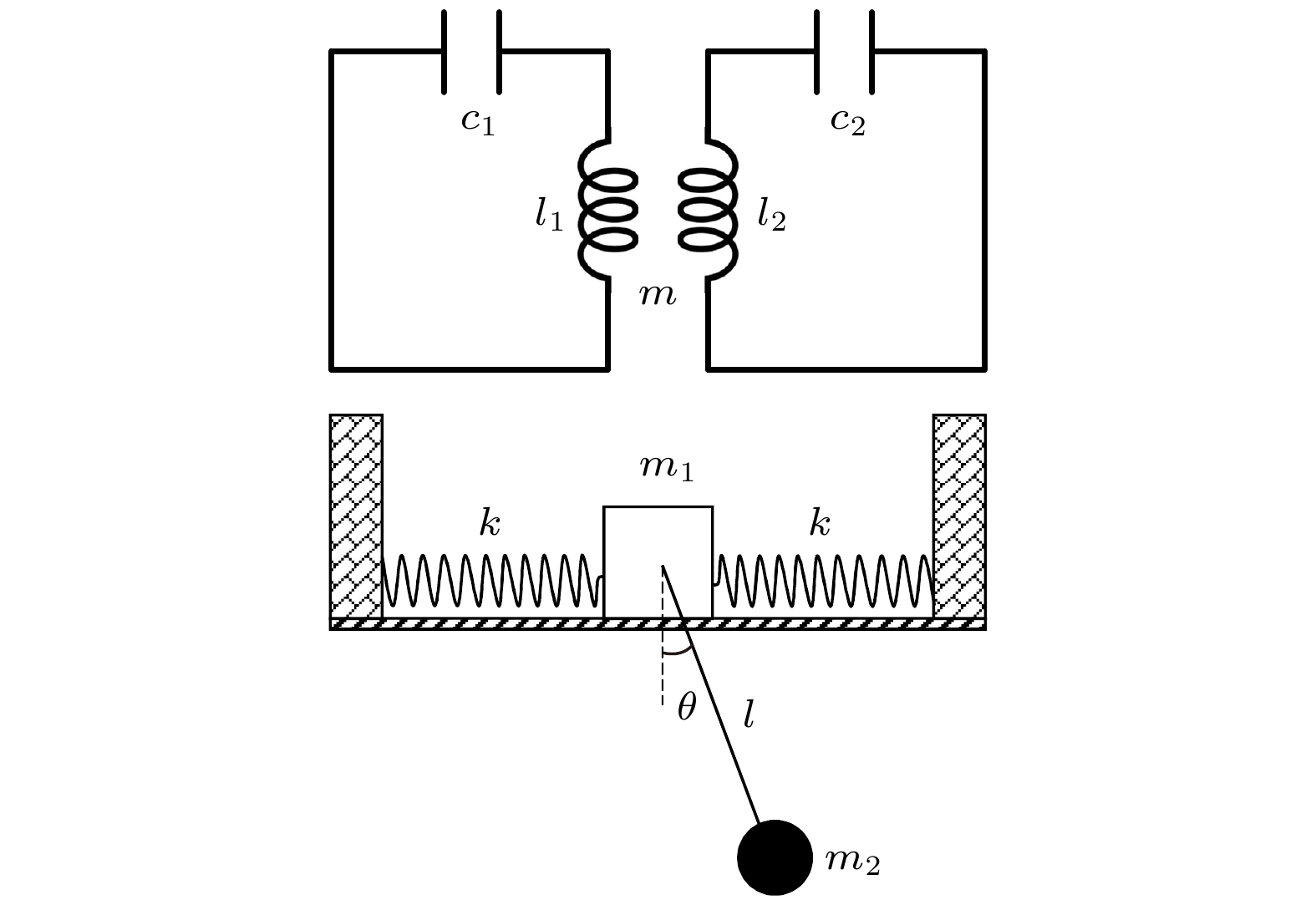
-
从量子力学诞生日起, 它的经典对应(或类比)一直是物理学家关心的话题. 本文以介观电路量子化的框架中, 带有互感的两个介观电容-电感(LC)电路为例, 首次讨论了量子纠缠的经典类比(或对应)问题. 先用有序算符内的积分理论证明其互感是产生量子纠缠的源头; 再推导出求解特征频率的公式, 就发现它与一个经典系统的小振动频率的表达式有相似之处, 该经典系统组成如下: 两个墙壁各连一个相同的弹簧, 两个弹簧之间接着一个滑动小车可以在光滑的桌面上运动, 小车挂有一根单摆. 用分析力学求此系统的小振动频率, 发现与上述介观电路的特征频率形式类似, 单摆的摆动会造成小车来回振动, 摆、小车和弹簧的互相牵制效应反映了小车和摆的“纠缠”.Since the birth of quantum mechanics, its classical correspondence (or analogy) has been a hot topic for physicists. In this paper, we first discuss whether there is a classical correspondence of quantum entanglement. We give a positive answer through the following examples: in the framework of quantization of mesoscopic circuits, two mesoscopic capacitance inductance (LC) circuits with mutual inductance are proved to be the source of quantum entanglement by using the integration within an ordered product, and then the formula of their characteristic frequency is obtained, It is found that it is similar to the expression of the small oscillating frequency of a classical system described below. The classical system is shown in
Fig. 1 . Two walls are connected with the same spring. And between the two springs a sliding trolley can move on a smooth table. The trolley is hung with a simple pendulum, The small oscillating frequency of the system is calculated by analytical mechanics. It is found that the swing of the simple pendulum will cause the trolley to oscillate back and forth. The mutual restraint effect of the pendulum, the trolley and the spring reflects the “entanglement” between them.-
Keywords:
- quantum disentangling operator /
- quantum noise /
- characteristic frequency /
- the IWOP method
[1] Srivastava Y, Widom A 1987 Phys. Rep. 148 1
Google Scholar
[2] Buot F A 1993 Phys. Rep. 234 73
Google Scholar
[3] Louisell W H 1973 Quantum Statistical Properties of Radiation (New York: John Wiley)
[4] Fan H Y, Liang X T 2000 Chin. Phys. Lett. 17 174
Google Scholar
[5] Fan H Y, Da C 2019 Optik 179 413
Google Scholar
[6] Wang J S, Fan H Y, Meng X G 2010 Chin. Phys. B 19 034206
Google Scholar
[7] Fan H Y, Klauder J R 1994 Phys. Rev. A 49 704
Google Scholar
[8] Fan H Y, Lu H L, Fan Y 2006 Ann. Phys. 321 480
Google Scholar
[9] Fan H Y, Xu Z H 1994 Phys. Rev. A 50 2921
Google Scholar
[10] Meng X G, Wang J S, Zhang X Y, Liang B L 2011 J. Phys. B: At. Mol. Opt. Phys. 44 165506
Google Scholar
[11] Zhang R, Meng X G, Du C X, Wang J S 2018 J. Phys. Soc. Jpn. 87 024001
Google Scholar
[12] Loudon R, Knight P L 1987 J. Mod. Opt. 34 709
Google Scholar
[13] Fan H Y 1992 Eur. Phys. Lett. 19 443
Google Scholar
[14] Meng X G, Wang Z, Wang J S, Fan H Y 2012 J. Opt. Soc. Am. B 29 1835
Google Scholar
[15] Zhao M J, Ma T, Ma Y Q 2018 Sci. China-Phys. Mech. Astron. 61 020311
Google Scholar
[16] Meng X G, Wang Z, Fan H Y, Wang J S, Yang Z S 2012 J. Opt. Soc. Am. B 29 1844
Google Scholar
[17] Meng X G, Wang J S, Liang B L, Du C X 2018 J. Exp. Theor. Phys. 154 NN8
[18] Meng X G, Xu Y J 2014 Int. J. Theor. Phys. 53 1239
Google Scholar
[19] Meng X G, Wang J S, Liang B L 2009 Solid State Commun. 149 2027
Google Scholar
[20] Wang J S, Meng X G, Fan H Y 2017 J. Mod. Opt. 64 1398
Google Scholar
[21] Fan H Y, Zhou J 2012 Sci. China-Phys. Mech. Astron. 55 605
Google Scholar
[22] Fan H Y 2012 Sci. China-Phys. Mech. Astron. 55 762
Google Scholar
-
图 1 带有互感的两个介观电容-电感(LC)回路及经典系统的小振动模型
Fig. 1. Two mesoscopic capacitance-inductor (LC) circuits with mutual inductance and Small vibration model of classical system
-
[1] Srivastava Y, Widom A 1987 Phys. Rep. 148 1
Google Scholar
[2] Buot F A 1993 Phys. Rep. 234 73
Google Scholar
[3] Louisell W H 1973 Quantum Statistical Properties of Radiation (New York: John Wiley)
[4] Fan H Y, Liang X T 2000 Chin. Phys. Lett. 17 174
Google Scholar
[5] Fan H Y, Da C 2019 Optik 179 413
Google Scholar
[6] Wang J S, Fan H Y, Meng X G 2010 Chin. Phys. B 19 034206
Google Scholar
[7] Fan H Y, Klauder J R 1994 Phys. Rev. A 49 704
Google Scholar
[8] Fan H Y, Lu H L, Fan Y 2006 Ann. Phys. 321 480
Google Scholar
[9] Fan H Y, Xu Z H 1994 Phys. Rev. A 50 2921
Google Scholar
[10] Meng X G, Wang J S, Zhang X Y, Liang B L 2011 J. Phys. B: At. Mol. Opt. Phys. 44 165506
Google Scholar
[11] Zhang R, Meng X G, Du C X, Wang J S 2018 J. Phys. Soc. Jpn. 87 024001
Google Scholar
[12] Loudon R, Knight P L 1987 J. Mod. Opt. 34 709
Google Scholar
[13] Fan H Y 1992 Eur. Phys. Lett. 19 443
Google Scholar
[14] Meng X G, Wang Z, Wang J S, Fan H Y 2012 J. Opt. Soc. Am. B 29 1835
Google Scholar
[15] Zhao M J, Ma T, Ma Y Q 2018 Sci. China-Phys. Mech. Astron. 61 020311
Google Scholar
[16] Meng X G, Wang Z, Fan H Y, Wang J S, Yang Z S 2012 J. Opt. Soc. Am. B 29 1844
Google Scholar
[17] Meng X G, Wang J S, Liang B L, Du C X 2018 J. Exp. Theor. Phys. 154 NN8
[18] Meng X G, Xu Y J 2014 Int. J. Theor. Phys. 53 1239
Google Scholar
[19] Meng X G, Wang J S, Liang B L 2009 Solid State Commun. 149 2027
Google Scholar
[20] Wang J S, Meng X G, Fan H Y 2017 J. Mod. Opt. 64 1398
Google Scholar
[21] Fan H Y, Zhou J 2012 Sci. China-Phys. Mech. Astron. 55 605
Google Scholar
[22] Fan H Y 2012 Sci. China-Phys. Mech. Astron. 55 762
Google Scholar
下载:
计量
- 文章访问数: 4284
- PDF下载量: 109
- 被引次数: 0
