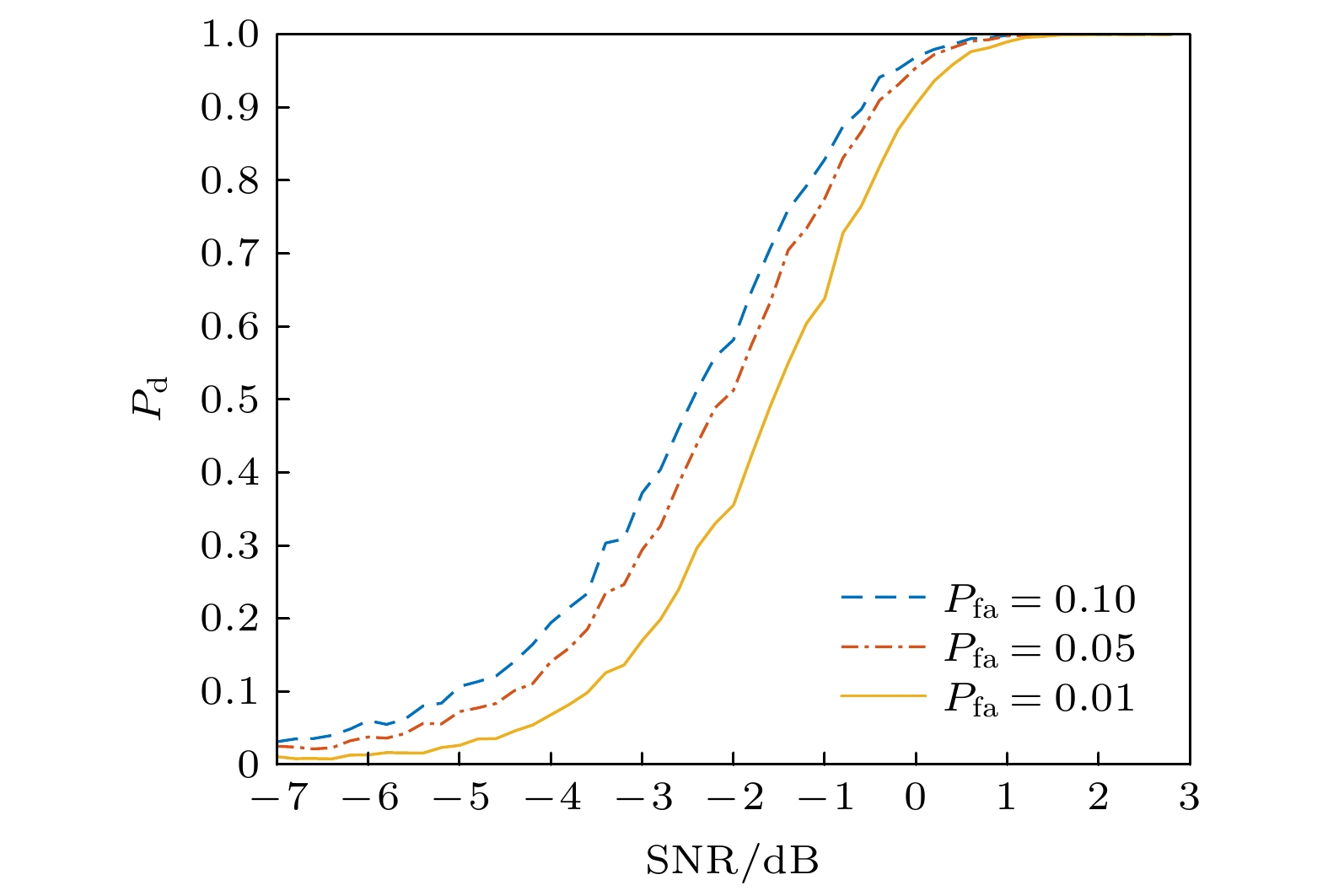
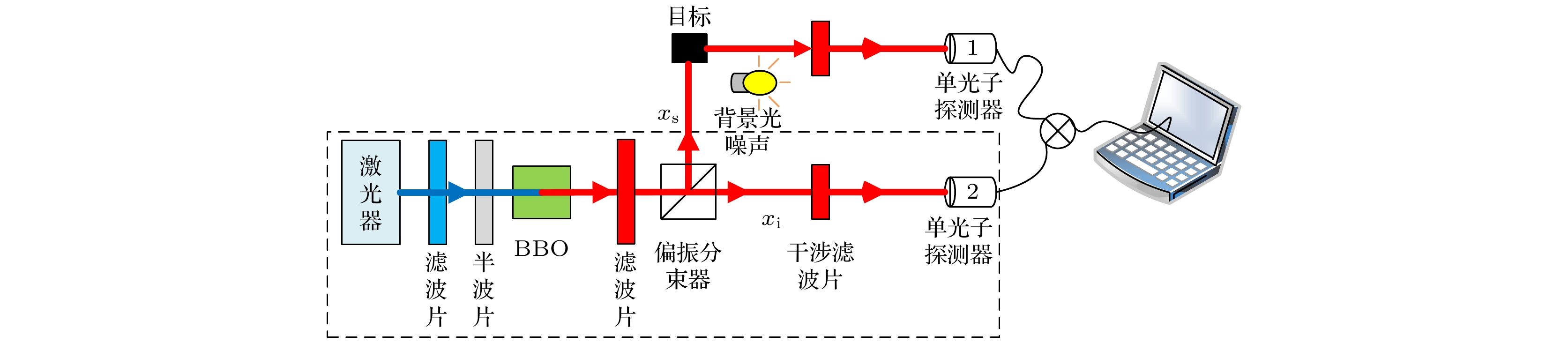
-
纠缠态量子探测是将量子力学与信息科学相结合, 应用在目标探测领域的一种新技术, 其在灵敏度、抗干扰能力等方面具有突破传统探测技术的潜力. 在雷达探测领域, 恒虚警检测是一项具有重要的意义和应用价值的技术. 然而, 对于纠缠态量子探测系统中恒虚警检测方法的研究还没有展开, 本文针对这一问题, 提出了一种纠缠态量子探测系统的恒虚警检测方法. 该方法通过系统对噪声的实时估计, 自适应调整检测门限, 使得纠缠态量子探测系统在检测过程中始终保持恒定的虚警概率. 仿真结果表明, 所提恒虚警检测方法是正确和有效的, 能够实现纠缠态量子探测系统的恒虚警检测功能. 该方法提升了纠缠态量子探测系统的灵活性和适应性, 为量子探测技术进一步走向实用及应用奠定了理论基础.Entangled state quantum detection is a new technology that combines quantum mechanics with information science, and is used in the field of target detection. It has the potential to break through traditional detection technologies in terms of sensitivity and anti-interference ability. In the field of radar detection, constant false alarm rate is a technology with important significance and application value. However, there is no research on the method of the constant false alarm rate in the entangled state quantum detection system. Aiming at this problem, in this paper a method of constant false alarm rate for the entangled state quantum detection system is proposed. In the proposed method the system's real-time estimation of noise is adopted, and the detection threshold is adjusted adaptively, so that the entangled state quantum detection system always maintains a constant false alarm rate. The simulation results show that the proposed method of constant false alarm rate is correct and effective, and can realize the function of the constant false alarm rate of the entangled state quantum detection system. The proposed method effectively improves the flexibility and adaptability of the quantum detection system, and provides a solid theoretical foundation for the practical application of entangled state quantum detection technology.
-
Keywords:
- quantum detection /
- entangled state /
- constant false alarm rate
[1] Giovannetti V, Lloyd S, Maccone L 2004 Science 306 5700
[2] Dutton Z, Shapiro J H, Guha S 2010 J. Opt. Soc. Am. B 27 A63
Google Scholar
[3] Lloyd S 2008 Science 321 1463
Google Scholar
[4] Smith J F 2009 Proceedings of SPIE-The International Society for Optical Engineering (Belingham, WA: SPIE) p7342
[5] Shapiro J H 2020 IEEE Trans. Aerosp. Electron. Syst. 35 8
[6] Tan S H, Erkmen B, Giovannetti V, Guha S, Lloyd S, Maccone L, Pirandola S, Jeffrey H S 2008 Phys. Rev. Lett. 101 253601
Google Scholar
[7] Lopaeva E D, Berchera I R, Degiovanni I P, Olivares S, Genovese M 2013 Phys. Rev. Lett. 110 153603
Google Scholar
[8] Barzanjeh S, Guha S, Weedbrook C, Vitali D, Shapiro J H, Pirandola S 2015 Physics 171 1029
[9] England D G, Balaji B, Sussman B J 2018 Phys. Rev. A 99 023828
[10] Barzanjeh S, Pirandola S, Vitali D, Fink J M 2019 Sci. Adv. 6 eabb0451
[11] Morris P A, Aspden R S, Bell J, Boyd R W, Padgett M J 2015 Nat. Commun. 6 5913
Google Scholar
[12] Clemente P, V Durán, Torres-Company V, Tajahuerce E, Lancis J 2010 Opt. Lett. 35 2391
Google Scholar
[13] 王书, 任益充, 饶瑞中, 苗锡奎 2017 66 150301
Google Scholar
Wang S, Ren Y C, Rao R Z, Miao X K 2017 Acta Phys. Sin. 66 150301
Google Scholar
[14] 任益充, 王书, 饶瑞中, 苗锡奎 2018 67 140301
Google Scholar
Ren Y C, Wang S, Rao R Z, Miao X K 2018 Acta Phys. Sin. 67 140301
Google Scholar
[15] Rohling H 1983 IEEE Trans. Aerosp. Electron. Syst. AES-19 608
Google Scholar
[16] Ghosh R, Mandel L 1987 Phys. Rev. Lett. 59 1903
Google Scholar
[17] Ou Z Y, Mandel L 1988 Phys. Rev. Lett. 61 50
Google Scholar
[18] Walborn S P, Monken C H, Pádua S, Ribeiro P 2010 Phys. Rep. 495 87
Google Scholar
[19] Howell J C, Bennink R S, Bentley S J, Boyd R W 2004 Phys. Rev. Lett. 9 210403
[20] Maclean J, Donohue J M, Resch K J 2018 Phys. Rev. Lett. 120 053601
Google Scholar
[21] 杜亚男, 解文钟, 金璇, 王金东, 魏正军, 秦晓娟, 赵峰, 张智明 2015 64 110301
Google Scholar
Du Y N, Xie W Z, Jin X, Wang J D, Wei Z J, Qin X J, Zhao F, Zhang Z M 2015 Acta Phys. Sin. 64 110301
Google Scholar
[22] 吴承峰, 杜亚男, 王金东, 魏正军, 秦晓娟, 赵峰, 张智明 2016 65 100302
Google Scholar
Wu C F, Du Y N, Wang J D, Wei Z J, Qin X J, Zhao F, Zhang Z M 2016 Acta Phys. Sin. 65 100302
Google Scholar
[23] 东晨, 赵尚弘, 张宁, 董毅, 赵卫虎, 刘韵 2014 63 200304
Google Scholar
Dong C, Zhao S H, Zhang N, Dong Y, Zhao W H, Liu Y 2014 Acta Phys. Sin. 63 200304
Google Scholar
[24] 周媛媛, 周学军 2011 60 100301
Google Scholar
Zhou Y Y, Zhou X J 2011 Acta Phys. Sin. 60 100301
Google Scholar
[25] 张东升, 权菊香, 周春源, 丁良恩 2006 量子光学学报 12 135
Google Scholar
Zhang D S, Quan J X, Zhou C Y, Ding L E 2006 J. Quantum Opt. 12 135
Google Scholar
-
图 2 基于符合计数的量子探测系统恒虚警检测原理
Fig. 2. Principle of CFAR detection of TCSPC based quantum detection system.
图 3 信号源纠缠光子数M与接收端符合噪声和信号光子数的关系 (a) M = 1000; (b) M = 3000
Fig. 3. Relationship between the number of entangled photons M of the signal source and the number of noise and signal photons at the receiver: (a) M = 1000; (b) M = 3000.
图 4 检测概率Pd与信号源纠缠光子数M及目标反射率
$ \eta $ 的关系Fig. 4. Relationship between the detection probability Pd and the number of entangled photons M of the signal source and the reflectivity of the target
$ \eta $ .
图 5 纠缠态量子探测系统恒虚警检测过程仿真
Fig. 5. Simulation of constant false alarm detection process of entangled state quantum detection system.
图 6 不同虚警概率下, 信噪比与检测概率的关系
Fig. 6. Relationship between signal-to-noise ratio and detection probability under different false alarm rate.
-
[1] Giovannetti V, Lloyd S, Maccone L 2004 Science 306 5700
[2] Dutton Z, Shapiro J H, Guha S 2010 J. Opt. Soc. Am. B 27 A63
Google Scholar
[3] Lloyd S 2008 Science 321 1463
Google Scholar
[4] Smith J F 2009 Proceedings of SPIE-The International Society for Optical Engineering (Belingham, WA: SPIE) p7342
[5] Shapiro J H 2020 IEEE Trans. Aerosp. Electron. Syst. 35 8
[6] Tan S H, Erkmen B, Giovannetti V, Guha S, Lloyd S, Maccone L, Pirandola S, Jeffrey H S 2008 Phys. Rev. Lett. 101 253601
Google Scholar
[7] Lopaeva E D, Berchera I R, Degiovanni I P, Olivares S, Genovese M 2013 Phys. Rev. Lett. 110 153603
Google Scholar
[8] Barzanjeh S, Guha S, Weedbrook C, Vitali D, Shapiro J H, Pirandola S 2015 Physics 171 1029
[9] England D G, Balaji B, Sussman B J 2018 Phys. Rev. A 99 023828
[10] Barzanjeh S, Pirandola S, Vitali D, Fink J M 2019 Sci. Adv. 6 eabb0451
[11] Morris P A, Aspden R S, Bell J, Boyd R W, Padgett M J 2015 Nat. Commun. 6 5913
Google Scholar
[12] Clemente P, V Durán, Torres-Company V, Tajahuerce E, Lancis J 2010 Opt. Lett. 35 2391
Google Scholar
[13] 王书, 任益充, 饶瑞中, 苗锡奎 2017 66 150301
Google Scholar
Wang S, Ren Y C, Rao R Z, Miao X K 2017 Acta Phys. Sin. 66 150301
Google Scholar
[14] 任益充, 王书, 饶瑞中, 苗锡奎 2018 67 140301
Google Scholar
Ren Y C, Wang S, Rao R Z, Miao X K 2018 Acta Phys. Sin. 67 140301
Google Scholar
[15] Rohling H 1983 IEEE Trans. Aerosp. Electron. Syst. AES-19 608
Google Scholar
[16] Ghosh R, Mandel L 1987 Phys. Rev. Lett. 59 1903
Google Scholar
[17] Ou Z Y, Mandel L 1988 Phys. Rev. Lett. 61 50
Google Scholar
[18] Walborn S P, Monken C H, Pádua S, Ribeiro P 2010 Phys. Rep. 495 87
Google Scholar
[19] Howell J C, Bennink R S, Bentley S J, Boyd R W 2004 Phys. Rev. Lett. 9 210403
[20] Maclean J, Donohue J M, Resch K J 2018 Phys. Rev. Lett. 120 053601
Google Scholar
[21] 杜亚男, 解文钟, 金璇, 王金东, 魏正军, 秦晓娟, 赵峰, 张智明 2015 64 110301
Google Scholar
Du Y N, Xie W Z, Jin X, Wang J D, Wei Z J, Qin X J, Zhao F, Zhang Z M 2015 Acta Phys. Sin. 64 110301
Google Scholar
[22] 吴承峰, 杜亚男, 王金东, 魏正军, 秦晓娟, 赵峰, 张智明 2016 65 100302
Google Scholar
Wu C F, Du Y N, Wang J D, Wei Z J, Qin X J, Zhao F, Zhang Z M 2016 Acta Phys. Sin. 65 100302
Google Scholar
[23] 东晨, 赵尚弘, 张宁, 董毅, 赵卫虎, 刘韵 2014 63 200304
Google Scholar
Dong C, Zhao S H, Zhang N, Dong Y, Zhao W H, Liu Y 2014 Acta Phys. Sin. 63 200304
Google Scholar
[24] 周媛媛, 周学军 2011 60 100301
Google Scholar
Zhou Y Y, Zhou X J 2011 Acta Phys. Sin. 60 100301
Google Scholar
[25] 张东升, 权菊香, 周春源, 丁良恩 2006 量子光学学报 12 135
Google Scholar
Zhang D S, Quan J X, Zhou C Y, Ding L E 2006 J. Quantum Opt. 12 135
Google Scholar
下载:
计量
- 文章访问数: 5285
- PDF下载量: 100
- 被引次数: 0
