热尘埃等离子体中(2 + 1)维尘埃声孤波的传播特征

林麦麦; 付颖捷; 宋秋影; 于腾萱; 文惠珊; 蒋蕾

doi:10.7498/aps.71.20210902

摘要

研究了由尘埃颗粒、电子和非热离子所组成的非磁化热尘埃等离子体中(2 + 1)维非线性尘埃声孤波的传播特征. 首先, 利用约化摄动法推导得到了用来描述(2 + 1)维非线性尘埃声孤波的Kadomtsev-Petviashvili (KP)方程, 并采用行波解法进行了定性分析, 从而获得了该系统的相图及Sagdeev势方程; 然后, 利用数学软件的数值模拟分析方法讨论了等温和绝热两种状态下, 热尘埃等离子体系统中不同参数对KP方程的非线性系数、色散系数、系统相图、Sagdeev势函数及孤立波解的影响. 最终, 研究结果表明: 等温和绝热状态下, 尘埃颗粒的质量、电子和非热离子的温度、数密度及分布状态等多种系统参数对非线性尘埃声孤波的振幅、宽度及波形等传播特征均存在重要影响.

关键词:

Abstract

The propagation characteristics of (2 + 1) dimensional nonlinear dust acoustic solitary wave in an unmagnetized hot dusty plasma composed of dust particles, electrons and nonthermal ions are studied in the paper. Firstly, the Kadomtsev-Petviashvili (KP) equation, which is used to describe the (2 + 1) dimensional nonlinear dust acoustic solitary wave, is derived by the reduced perturbation method, and the phase diagram and the Sagdeev potential equation of the system are obtained by using the traveling wave solution method. Then, the effects of different parameters in the hot dusty plasma system on the nonlinear coefficient, dispersion coefficient of the KP equation, system phase diagrams, Sagdeev potential function and the solitary wave solution in isothermal and adiabatic states are discussed by using numerical simulation and analysis method of mathematical software. Finally, the results show that the mass of dust particles, temperature, number density and distribution state of electrons and nonthermal ions have important effects on the amplitude, width and waveform of the nonlinear dust acoustic solitary wave under isothermal and adiabatic conditions.

Keywords:

作者及机构信息

西北师范大学物理与电子工程学院, 兰州　730070

通信作者: 林麦麦, linmaimai1514@126.com

基金项目: 国家自然科学基金(批准号: 11205124)资助的课题

Authors and contacts

College of Physics and Electronic Engineering, Northwest Normal University, Lanzhou 730070, China

Corresponding author: Lin Mai-Mai, linmaimai1514@126.com

Funds: Project supported by the National Natural Science Foundation of China (Grant No. 11205124)

文章全文 : translate this paragraph

参考文献

[1]	Rosenberg M, Kalman G 1997 Phys. Rev. E 56 7166 Google Scholar
[2]	Gill T S, Bains A S, Bedi C 2010 Phys. Plasmas 17 013701 Google Scholar
[3]	El-Taibany W F, El-Bedwehy N A, El-Shamy E F 2011 Phys. Plasmas 18 033703 Google Scholar
[4]	Sabry R, Moslem W M, Shukla P K 2009 Phys. Plasmas 16 032302 Google Scholar
[5]	Singh K, Kaur N, Saini N S 2017 Phys. Plasmas 24 063703 Google Scholar
[6]	Melandsø F, Goree J 1995 Phys. Rev. E 52 5312
[7]	Gurnett D A, Ansher J A, Kurth W S, Granroth L J 1997 Geophys. Res. Lett. 24 3125
[8]	Rao N N, Shukla P K, Yu M Y 1990 Planet. Space Sci. 38 543 Google Scholar
[9]	Barkan A, Merlino R L, Angelo D N 1995 Phys. Plasmas 2 3563 Google Scholar
[10]	Ma J X, Liu J 1997 Phys. Plasmas 4 253 Google Scholar
[11]	Xie B S, He K F, Huang Z Q 1998 Chin. Phys. Lett. 15 892 Google Scholar
[12]	El-Taibany W F 2013 Phys. Plasmas 20 093701 Google Scholar
[13]	Paul A, Mandal G, Mamun A A, Amin M R 2013 Phys. Plasmas 20 104505 Google Scholar
[14]	El-Labany S K, El-Taibany W F, El-Tantawy A A, Zedan N A 2020 Contrib. Plasma Phys. 60 e202000049
[15]	Schamel H 1986 Phys. Rep. 140 161 Google Scholar
[16]	Ghosh S, Bharuthram R, Khan M, Gupta M R 2004 Phys. Plasmas 11 3602 Google Scholar
[17]	El-Taibany W F, Wadati Miki, Sabry R 2007 Phys. Plasmas 14 032304
[18]	Ghosh U N, Chatterjee P 2012 Indian J. Phys. 86 407 Google Scholar
[19]	Bliokh P V, Yaroshenko V V 1985 Sov. Astron. 29 330
[20]	Seadawy A R, Lu D 2016 Results Phys. 6 590 Google Scholar
[21]	Bhakta S, Ghosh U, Sarkar S 2017 Phys. Plasmas 24 023704 Google Scholar
[22]	Iqbal M, Seadawy A R, Lu D, Xia X 2019 Mod. Phys. Lett. A 34 1950309 Google Scholar
[23]	El-Bedwehy N A, El-Taibany W F 2020 Phys. Plasmas 27 012107 Google Scholar
[24]	Tasnim I, Masud M M, Mamun A A 2014 J. Korean Phys. Soc. 64 987 Google Scholar
[25]	Emamuddin M, Mamun A A 2018 Phys. Plasmas 25 013708 Google Scholar
[26]	Mendoza-Briceño C A, Russel S M, Mamun A A 2000 Planet. Space Sci. 48 599 Google Scholar
[27]	王红艳, 段文山 2007 56 3977 Google Scholar Wang H Y, Duan W S 2007 Acta Phys. Sin. 56 3977 Google Scholar
[28]	Mamun A A, Cairns R A, Shukla P K 1996 Phys. Plasmas 3 2610 Google Scholar
[29]	Cairns R A, Mamun A A, Bingham R, Bostrom R, Dendy R O, Nairn C M C, Shukla P K 1995 Geophys. Res. Lett. 22 2709 Google Scholar
[30]	Mamuna A A, Russell S M, Cesar A, Mendoza-Briceño C A, Alamb M N, Datta T K, Das A K 2000 Planet. Space Sci. 48 163 Google Scholar
[31]	Kotsarenko N Ya, Koshevaya S V, Stewart G A, Maravilla D 1998 Planet. Space Sci. 46 429 Google Scholar
[32]	Wang Z, Gurnett D A, Averkamp T F, Persoon A M, Kurth W S 2006 Planet. Space Sci. 54 957 Google Scholar
[33]	Pickett J S, Kurth W S, Gurnett D A, Huff R L, Faden J B, Averkamp T F, Píša D, Jones G H 2015 J. Geophys. Res. Space Phys. 120 6569 Google Scholar
[34]	El-Labany S K, Safi F M, Moslem W M 2007 Planet. Space Sci. 55 2192 Google Scholar
[35]	Mamun A A, Shukla P K 2011 J. Plasma Phys. 77 437 Google Scholar

施引文献

图 1 ${\sigma _{\rm{d}}}$取值不同时, 非线性系数A随参数α的变化 (a) 等温状态, $\gamma = 1$; (b) 绝热状态, $\gamma = 3$

Fig. 1. Nonlinear coefficient A with respect to the parameter α for different values of ${\sigma _{\rm{d}}}$: (a) Isothermal state; (b) adiabatic state.

下载: 全尺寸图片幻灯片

图 2 (a)—(c) ${m_{\rm{d}}}, \;\mu, \;{\sigma _{\rm{i}}}$取值不同时, 等温状态($\gamma = 1$)下非线性系数A随参数α的变化

Fig. 2. Nonlinear coefficient A with respect to the parameter α in isothermal state under the condition of different values of (a)−(c) ${m_{\rm{d}}}, \;\mu, \;{\sigma _{\rm{i}}}$.

下载: 全尺寸图片幻灯片

图 3 (a)—(c) ${m_{\rm{d}}}, \;\mu, \;{\sigma _{\rm{i}}}$取值不同时, 绝热状态($\gamma = 3$)下非线性系数A随参数α的变化

Fig. 3. Nonlinear coefficient A with respect to the parameter α in adiabatic state under the condition of different values of (a)−(c) ${m_{\rm{d}}}, \;\mu, \;{\sigma _{\rm{i}}}$.

下载: 全尺寸图片幻灯片

图 4 色散系数B随参数${v_0}$的变化　(a), (b) 等温状态, $\gamma = 1$; (c), (d) 绝热状态, $\gamma = 3$

Fig. 4. Dispersion coefficient A with respect to the parameter ${v_0}$ in (a), (b) isothermal state and (c), (d) adiabatic state, respectively.

下载: 全尺寸图片幻灯片

图 5 相平面$\left( {{\phi _1}, \;\psi } \right)$及轨线分布图　(a)$ \gamma = 1 $ ; (b) $ \gamma = 3 $

Fig. 5. Track of phase plane: (a)$ \gamma = 1 $ ; (b) $ \gamma = 3 $.

下载: 全尺寸图片幻灯片

图 6 ${\sigma _{\rm{d}}}$取不同值时, 等温状态($\gamma = 1$)下Sagdeev势$V\left( {{\phi _1}} \right)$随${\phi _1}$的变化

Fig. 6. The Sagdeev potential $V\left( {{\phi _1}} \right)$ with respect to ${\phi _1}$ in isothermal state for different values of ${\sigma _{\rm{d}}}$.

下载: 全尺寸图片幻灯片

图 7 ${\sigma _{\rm{d}}}$取不同值时, 绝热状态($\gamma = 3$)下Sagdeev势$V\left( {{\phi _1}} \right)$随${\phi _1}$的变化

Fig. 7. The Sagdeev potential $V\left( {{\phi _1}} \right)$ with respect to ${\phi _1}$ in adiabatic state for different values of ${\sigma _{\rm{d}}}$.

下载: 全尺寸图片幻灯片

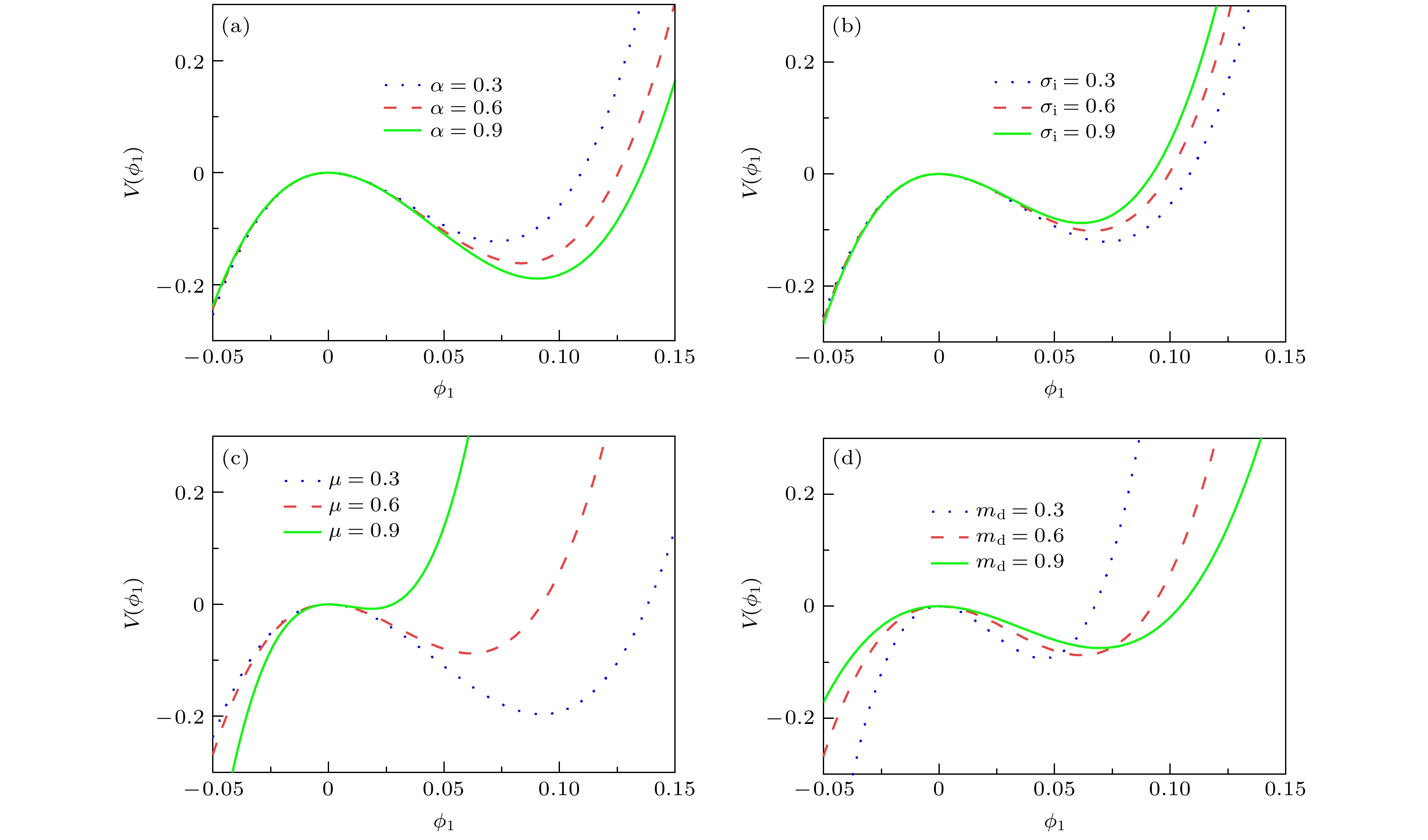
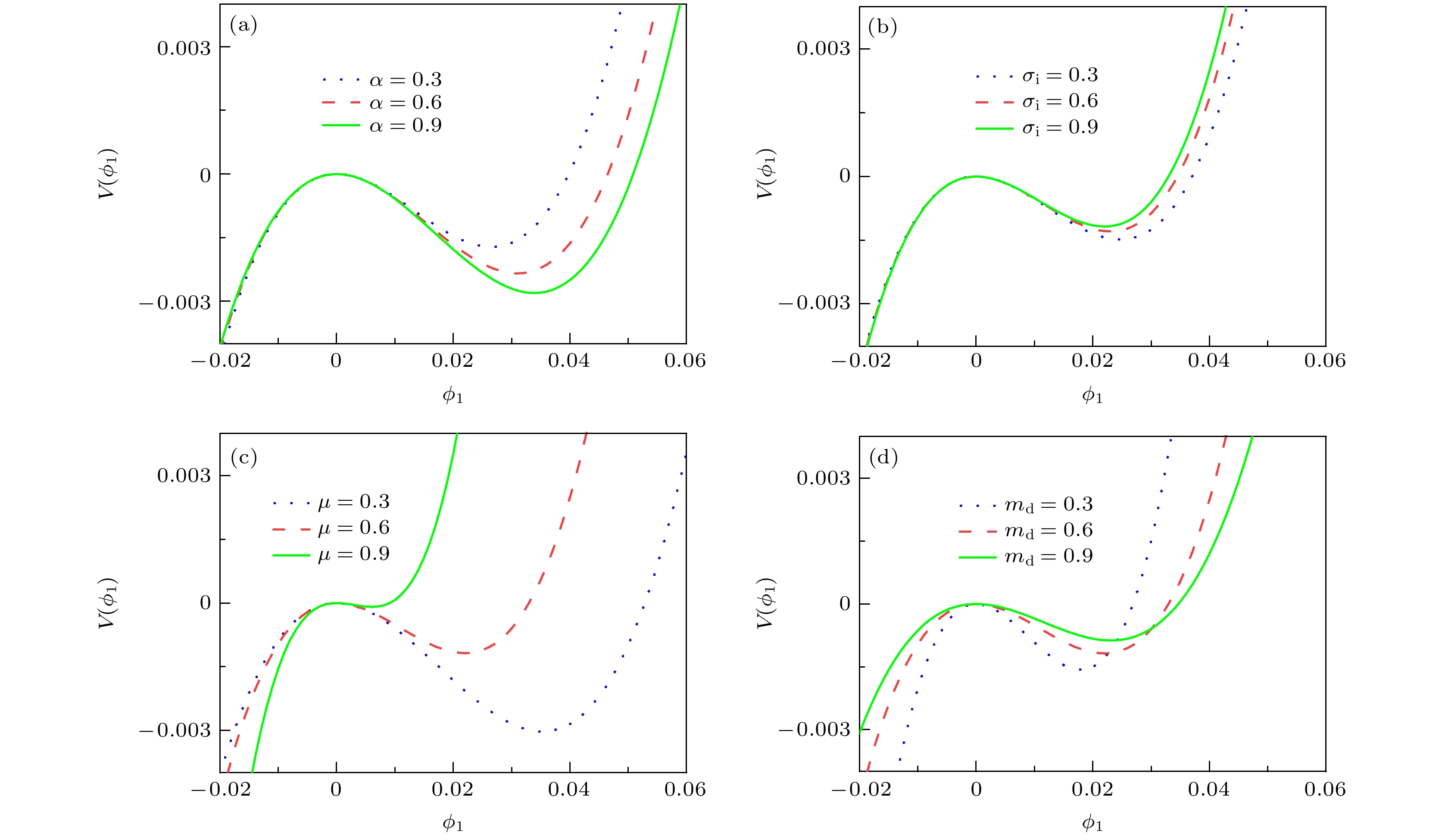
图 8 (a)—(d) $\alpha, \;{\sigma _{\rm{i}}}, \;\mu, \;{m_{\rm{d}}}$取不同值, 等温状态($\gamma = 1$)下Sagdeev势$V\left( {{\phi _1}} \right)$随$ {\phi _1} $的变化

Fig. 8. The Sagdeev potential $V\left( {{\phi _1}} \right)$ with respect to $ {\phi _1} $ in isothermal state under the condition of different values of (a)−(d) $\alpha, \;{\sigma _{\rm{i}}}, \;\mu, \;{m_{\rm{d}}}$.

下载: 全尺寸图片幻灯片

图 9 (a)—(d) $\alpha, \;{\sigma _{\rm{i}}}, \;\mu, \;{m_{\rm{d}}}$取不同值, 绝热状态($\gamma = 3$)下Sagdeev势$V\left( {{\phi _1}} \right)$随$ {\phi _1} $的变化

Fig. 9. The Sagdeev potential $V\left( {{\phi _1}} \right)$ with respect to $ {\phi _1} $ in adiabatic state under the condition of different values of (a)−(d) $\alpha, \;{\sigma _{\rm{i}}}, \;\mu, \;{m_{\rm{d}}}$.

下载: 全尺寸图片幻灯片

图 10 α取值不同时, 孤立波$ {\phi _1} $的波形变化　(a) 等温状态, $\gamma = 1$; (b) 绝热状态, $\gamma = 3$

Fig. 10. Waveform of solitary waves $ {\phi _1} $ for different values of α: (a) Isothermal state; (b) adiabatic state, respectively.

下载: 全尺寸图片幻灯片

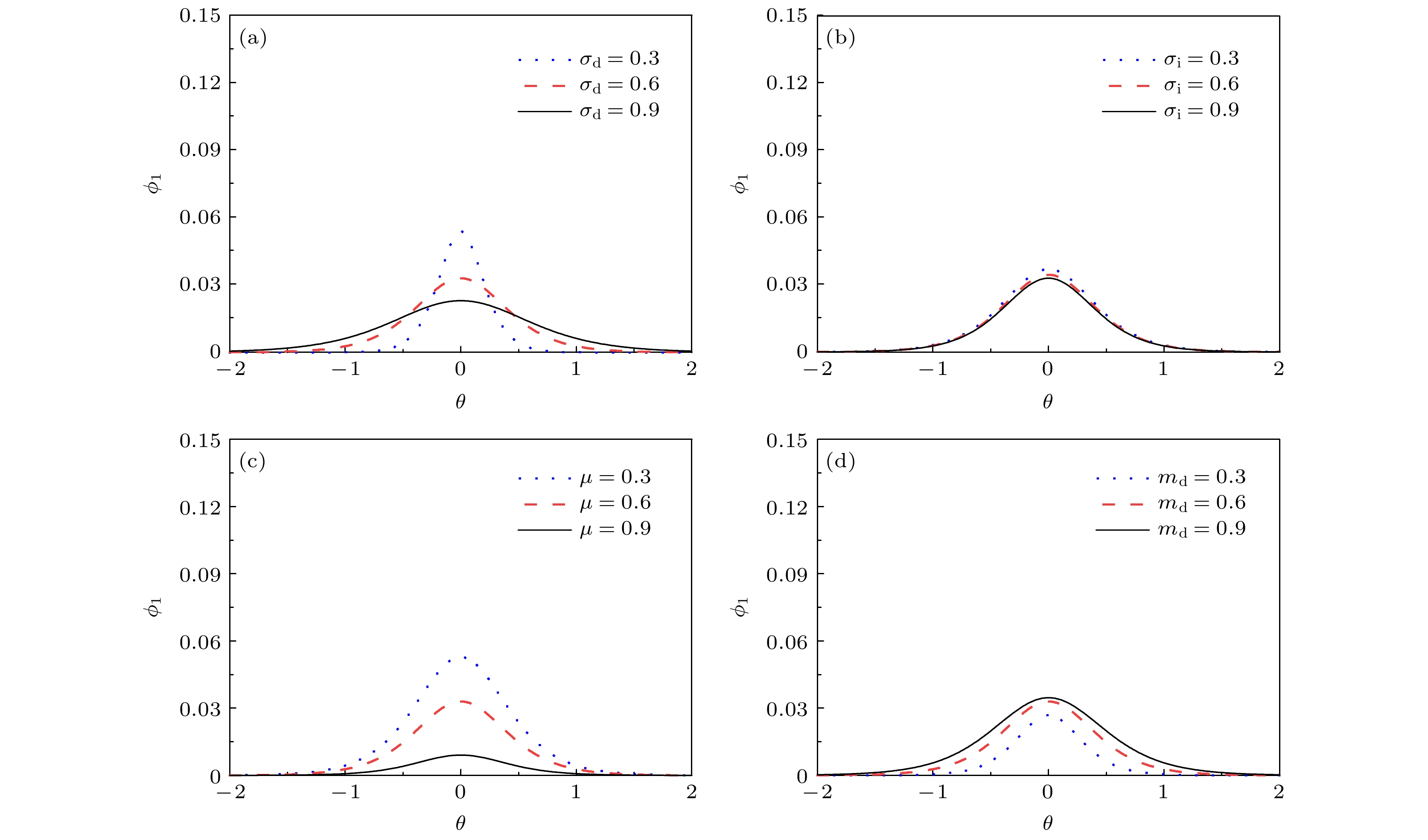
图 11 (a)—(d) ${\sigma _{\rm{d}}}, \;{\sigma _{\rm{i}}}, \;\mu, \;{m_{\rm{d}}}$取不同值时, 等温状态($\gamma = 1$)下孤立波$ {\phi _1} $的波形变化

Fig. 11. Waveform of solitary waves $ {\phi _1} $ in isothermal state under the condition of different values of (a)−(d) ${\sigma _{\rm{d}}}, \;{\sigma _{\rm{i}}}, \;\mu, \;{m_{\rm{d}}}$.

下载: 全尺寸图片幻灯片

图 12 (a)—(d) ${\sigma _{\rm{d}}}, \;{\sigma _{\rm{i}}}, \;\mu, \;{m_{\rm{d}}}$取不同值时, 绝热状态($\gamma = 3$)下孤立波$ {\phi _1} $的波形变化

Fig. 12. Waveform of solitary waves $ {\phi _1} $ in adiabatic state under the condition of different values of (a)−(d) ${\sigma _{\rm{d}}}, \;{\sigma _{\rm{i}}}, \;\mu, \;{m_{\rm{d}}}$.

下载: 全尺寸图片幻灯片

map

[1]	Rosenberg M, Kalman G 1997 Phys. Rev. E 56 7166 Google Scholar
[2]	Gill T S, Bains A S, Bedi C 2010 Phys. Plasmas 17 013701 Google Scholar
[3]	El-Taibany W F, El-Bedwehy N A, El-Shamy E F 2011 Phys. Plasmas 18 033703 Google Scholar
[4]	Sabry R, Moslem W M, Shukla P K 2009 Phys. Plasmas 16 032302 Google Scholar
[5]	Singh K, Kaur N, Saini N S 2017 Phys. Plasmas 24 063703 Google Scholar
[6]	Melandsø F, Goree J 1995 Phys. Rev. E 52 5312
[7]	Gurnett D A, Ansher J A, Kurth W S, Granroth L J 1997 Geophys. Res. Lett. 24 3125
[8]	Rao N N, Shukla P K, Yu M Y 1990 Planet. Space Sci. 38 543 Google Scholar
[9]	Barkan A, Merlino R L, Angelo D N 1995 Phys. Plasmas 2 3563 Google Scholar
[10]	Ma J X, Liu J 1997 Phys. Plasmas 4 253 Google Scholar
[11]	Xie B S, He K F, Huang Z Q 1998 Chin. Phys. Lett. 15 892 Google Scholar
[12]	El-Taibany W F 2013 Phys. Plasmas 20 093701 Google Scholar
[13]	Paul A, Mandal G, Mamun A A, Amin M R 2013 Phys. Plasmas 20 104505 Google Scholar
[14]	El-Labany S K, El-Taibany W F, El-Tantawy A A, Zedan N A 2020 Contrib. Plasma Phys. 60 e202000049
[15]	Schamel H 1986 Phys. Rep. 140 161 Google Scholar
[16]	Ghosh S, Bharuthram R, Khan M, Gupta M R 2004 Phys. Plasmas 11 3602 Google Scholar
[17]	El-Taibany W F, Wadati Miki, Sabry R 2007 Phys. Plasmas 14 032304
[18]	Ghosh U N, Chatterjee P 2012 Indian J. Phys. 86 407 Google Scholar
[19]	Bliokh P V, Yaroshenko V V 1985 Sov. Astron. 29 330
[20]	Seadawy A R, Lu D 2016 Results Phys. 6 590 Google Scholar
[21]	Bhakta S, Ghosh U, Sarkar S 2017 Phys. Plasmas 24 023704 Google Scholar
[22]	Iqbal M, Seadawy A R, Lu D, Xia X 2019 Mod. Phys. Lett. A 34 1950309 Google Scholar
[23]	El-Bedwehy N A, El-Taibany W F 2020 Phys. Plasmas 27 012107 Google Scholar
[24]	Tasnim I, Masud M M, Mamun A A 2014 J. Korean Phys. Soc. 64 987 Google Scholar
[25]	Emamuddin M, Mamun A A 2018 Phys. Plasmas 25 013708 Google Scholar
[26]	Mendoza-Briceño C A, Russel S M, Mamun A A 2000 Planet. Space Sci. 48 599 Google Scholar
[27]	王红艳, 段文山 2007 56 3977 Google Scholar Wang H Y, Duan W S 2007 Acta Phys. Sin. 56 3977 Google Scholar
[28]	Mamun A A, Cairns R A, Shukla P K 1996 Phys. Plasmas 3 2610 Google Scholar
[29]	Cairns R A, Mamun A A, Bingham R, Bostrom R, Dendy R O, Nairn C M C, Shukla P K 1995 Geophys. Res. Lett. 22 2709 Google Scholar
[30]	Mamuna A A, Russell S M, Cesar A, Mendoza-Briceño C A, Alamb M N, Datta T K, Das A K 2000 Planet. Space Sci. 48 163 Google Scholar
[31]	Kotsarenko N Ya, Koshevaya S V, Stewart G A, Maravilla D 1998 Planet. Space Sci. 46 429 Google Scholar
[32]	Wang Z, Gurnett D A, Averkamp T F, Persoon A M, Kurth W S 2006 Planet. Space Sci. 54 957 Google Scholar
[33]	Pickett J S, Kurth W S, Gurnett D A, Huff R L, Faden J B, Averkamp T F, Píša D, Jones G H 2015 J. Geophys. Res. Space Phys. 120 6569 Google Scholar
[34]	El-Labany S K, Safi F M, Moslem W M 2007 Planet. Space Sci. 55 2192 Google Scholar
[35]	Mamun A A, Shukla P K 2011 J. Plasma Phys. 77 437 Google Scholar

[1]	林麦麦, 宋晨光, 王明月, 陈富艳. 含有非热电子和陷俘离子的复杂等离子体中非线性尘埃声波的传播特征. , 2024, 73(7): 075201. doi: 10.7498/aps.73.20231967
[2]	张大军. 可积系统的双线性约化方法. , 2023, 72(10): 100203. doi: 10.7498/aps.72.20230063
[3]	林麦麦, 王明月, 蒋蕾. 多组分尘埃等离子体中非线性尘埃声孤波的传播特征. , 2023, 72(3): 035201. doi: 10.7498/aps.72.20221843
[4]	林麦麦, 蒋蕾, 宋秋影, 付颖捷, 王明月, 文慧珊, 于腾萱. 含有Kappa分布电子的多组分等离子体中的 (3 + 1) 维非线性离子声波. , 2022, 71(17): 175201. doi: 10.7498/aps.71.20212255
[5]	张海宝, 陈强. 非热等离子体材料表面处理及功能化研究进展. , 2021, 70(9): 095203. doi: 10.7498/aps.70.20202233
[6]	陈智敏, 段文山. 弹性管中的怪波. , 2020, 69(1): 014701. doi: 10.7498/aps.69.20191308
[7]	王子, 张丹妹, 任捷. 声子系统中弹性波与热输运的拓扑与非互易现象. , 2019, 68(22): 220302. doi: 10.7498/aps.68.20191463
[8]	欧阳成, 姚静荪, 石兰芳, 莫嘉琪. 一类尘埃等离子体孤波解. , 2014, 63(11): 110203. doi: 10.7498/aps.63.110203
[9]	欧阳成, 石兰芳, 林万涛, 莫嘉琪. (2+1)维扰动时滞破裂孤波方程行波解的摄动方法. , 2013, 62(17): 170201. doi: 10.7498/aps.62.170201
[10]	周先春, 林万涛, 林一骅, 莫嘉琪. 大气非均匀量子等离子体孤波解. , 2012, 61(24): 240202. doi: 10.7498/aps.61.240202
[11]	张娟, 周志刚, 石玉仁, 杨红娟, 段文山. 修正KP方程及其孤波解的稳定性. , 2012, 61(13): 130401. doi: 10.7498/aps.61.130401
[12]	莫嘉琪. 一类非线性尘埃等离子体孤波解. , 2011, 60(3): 030203. doi: 10.7498/aps.60.030203
[13]	张毅. Birkhoff系统约化的Routh方法. , 2008, 57(9): 5374-5377. doi: 10.7498/aps.57.5374
[14]	韩久宁, 王苍龙, 栗生长, 段文山. 二维热离子等离子体中离子声孤波的相互作用. , 2008, 57(10): 6068-6073. doi: 10.7498/aps.57.6068
[15]	何广军, 田多祥, 林麦麦, 段文山. 含有带正负电离子的等离子体中的非线性波研究. , 2008, 57(4): 2320-2327. doi: 10.7498/aps.57.2320
[16]	王红艳, 段文山. 对含有非热力学平衡离子的尘埃等离子体中孤波特性的理论研究. , 2007, 56(7): 3977-3983. doi: 10.7498/aps.56.3977
[17]	洪学仁, 段文山, 孙建安, 石玉仁, 吕克璞. 非均匀尘埃等离子体中孤子的传播. , 2003, 52(11): 2671-2677. doi: 10.7498/aps.52.2671
[18]	段文山, 洪学仁. 弱相对论等离子体横向扰动下的离子声孤波. , 2003, 52(6): 1337-1339. doi: 10.7498/aps.52.1337
[19]	侯伯宇, 李卫. 一种产生Einstein约化场方程解的方法. , 1987, 36(7): 930-934. doi: 10.7498/aps.36.930
[20]	张承福, 柯孚久. 非均匀磁化等离子体中的二维漂移孤波. , 1985, 34(3): 298-305. doi: 10.7498/aps.34.298

计量

文章访问数: 3672
PDF下载量: 54
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

热尘埃等离子体中(2 + 1)维尘埃声孤波的传播特征