含有非热电子和陷俘离子的复杂等离子体中非线性尘埃声波的传播特征

林麦麦; 宋晨光; 王明月; 陈富艳

doi:10.7498/aps.73.20231967

摘要

本文研究了同时含有非热(nonthermal)电子和陷俘(trapped)离子分布的复杂等离子体系统中非线性尘埃声波的传播特征. 首先, 利用线性化方法推导得到非线性尘埃声波的色散关系. 接着, 借助Sagdeev势方法推导得到表征非线性尘埃声波运动的二维自治系统、Sagdeev势方程和Sagdeev势函数的具体表达式. 然后, 依据数值模拟的方法分析了多种系统因素对二维自治系统相图的重要影响. 结果表明: 含有nonthermal电子和trapped离子的复杂等离子体系统中同时存在线性周期波、非线性周期波和孤立波. 接下来, 通过讨论Sagdeev势函数随系统参数的变化规律发现: 该复杂等离子体系统中仅存在振幅大于零的压缩型孤立波. 最后, 探讨多种系统因素对非线性尘埃声孤波的振幅、宽度和波形等传播特征的重要影响. 结果显示: 马赫数、nonthermal电子和trapped离子以及尘埃颗粒未扰动的数密度、温度及荷电量等参数对该复杂等离子体系统中非线性尘埃声孤波的振幅、宽度和波形等传播特性均具有显著影响, 且该结果与Sagdeev势函数的分析结果保持一致.

关键词:

Abstract

The propagation characteristics of nonlinear dust acoustic solitary waves in a complex plasma system with nonthermal electrons and trapped ions are investigate in this work. The nonlinear dispersion relation of dust acoustic waves is obtained by using the linear method, and the two-dimensional autonomous system governing the motion of nonlinear dust acoustic waves is derived by using the Sagdeev potential method. At the same time, the specific expression of the Sagdeev potential function is obtained based on the Sagdeev potential equation. The numerical simulations are used to analyze the phase portraits of the two-dimensional autonomous system, revealing the linear periodic wave orbits, nonlinear periodic wave orbits, and homoclinic orbits co-existing in the complex dusty plasma system with nonthermal electrons and trapped ions. Furthermore, from the variations of the Sagdeev potential function with different system parameters it follows that only the compressive solitary waves exist in this complex plasma system. The significant influences of various system parameters on the amplitude, width, and waveform of the nonlinear dust acoustic solitary wave in the complex plasma system are discussed in detail. The results demonstrate that the Mach number, the nonthermal electrons and trapped ions, undisturbed dust particle number density, temperature, and charge have important effects on the propagating characteristics of the nonlinear dust acoustic solitary waves in a complex plasma with nonthermal electrons and trapped ions.

Keywords:

nonlinear dust acoustic solitary waves /
Sagdeev potential method /
nonthermal electron distribution /
trapped ions distribution

作者及机构信息

西北师范大学物理与电子工程学院, 兰州　730070

通信作者: 林麦麦, linmaimai1514@126.com

Authors and contacts

College of Physics and Electronic Engineering, Northwest Normal University, Lanzhou 730070, China

Corresponding author: Lin Mai-Mai, linmaimai1514@126.com

文章全文 : translate this paragraph

参考文献

[1]	Gill T S, Bains A S, Bedi C 2010 Phys. Plasmas. 17 013701 Google Scholar
[2]	Zahed H, Emadi E 2016 Phys. Plasmas. 23 083706 Google Scholar
[3]	Singh K, Kaur N, Saini N S 2017 Phys. Plasmas. 24 063703 Google Scholar
[4]	Akhter T, Mannan A, Mamun A A 2013 Plasma. Phys. Rep. 39 548 Google Scholar
[5]	Anowarm G M, Mamuna A 2008 Phys. Lett. 372 5896 Google Scholar
[6]	Rasheed A, Tsintsadze N L, Murtaza G 2011 Phys. Plasmas. 18 112701 Google Scholar
[7]	Rao N N, Shukla P K, Yu M Y 1990 Planet. Space. Sci. 38 543 Google Scholar
[8]	Barkan A, Merlino R L, N D Angelo 1995 Phys. Plasmas 2 3563 Google Scholar
[9]	Xie B S, He K F, Huang Z Q 1998 Chin. Phys. Lett. 15 892 Google Scholar
[10]	Lin M M, Duan W S 2005 Commun. Theor. Phys. 44 719 Google Scholar
[11]	Murad A, Zakir U, Haque Q 2019 Braz. J. Phys. 49 79 Google Scholar
[12]	Sarmah B, Devi A, Sarma J 2019 InfoKara 8 115 Google Scholar
[13]	Soni P K, Aravindakshan H, Kakad B, Kakad A 2021 Phys. Scr. 96 105604 Google Scholar
[14]	Jahan S, Banik S, Chowdhury N A, Mannan A, Mamun A A 2022 Gases 2 22 Google Scholar
[15]	林麦麦, 付颖捷, 宋秋影, 于腾萱, 文惠珊, 蒋蕾 2022 71 095203 Google Scholar Lin M M, Fu Y J, Song Q Y, Yu T X, Wen H S, Jiang L 2022 Acta Phys. Sin. 71 095203 Google Scholar
[16]	林麦麦, 王明月, 蒋蕾 2023 72 035201 Google Scholar Lin M M, Wang M Y, Jiang L 2023 Acta Phys. Sin. 72 035201 Google Scholar
[17]	Mamani C 2023 Braz. J. Phys. 53 110 Google Scholar
[18]	Saha T, Chatterjee P 2009 Phys. Plasmas 16 013707 Google Scholar
[19]	Mamun A A, Shukla P K 2009 Phys. Rev. E 80 037401 Google Scholar
[20]	Selim M M 2016 Eur. Phys. J. Plus 131 93 Google Scholar
[21]	Gill T S, Kaur H, Bansal S, Saini N S, Bala P 2007 Eur. Phys. J. D 41 151 Google Scholar
[22]	Mamun A A, Alam M N, Azad A K 1998 Phys. Plasmas 5 1212 Google Scholar
[23]	Mandal D, Lesur M, Gravier E, Sama J N, Guillevic A, Sarazin Y 2023 Plasma Phys. Controlled Fusion 65 055001 Google Scholar
[24]	Kaniadakis G, Lavagno A, Quarati P 1996 Phys. Lett. B 369 308 Google Scholar
[25]	El-Labany S K, El-Taibany W F, El-Abbasy O M 2007 Chaos, Solitons Fractals 33 813 Google Scholar
[26]	Salam M A, Akbar M A, Ali M Z 2021 Results Phys. 26 104376 Google Scholar
[27]	Kian R B, Mahdieh M H 2023 Fluid Dyn. Res. 55 35503 Google Scholar
[28]	Taylor H A, Daniell R E, Hartle R E, Brinton H C, Bauer S J, Scarf F L 1981 Adv. Space Res. 1 247 Google Scholar
[29]	Sabry R, Moslem W M, Shukla P K 2009 Phys. Plasmas 16 032302 Google Scholar
[30]	Amour R, Tribeche M 2010 Plasma Phys. 17 063702 Google Scholar
[31]	Haider M M, Ferdous T, Duha S S 2014 Cent. Eur. J. Phys. 12 701 Google Scholar
[32]	Ghai Y, Saini S N 2017 Astrophys. Space Sci. 362 3 Google Scholar
[33]	Annou K, Bahamida S, Annou R 2011 Pramana-J. Phys. 76 513 Google Scholar
[34]	Mamun A A 1998 Phys. Scr. 57 258 Google Scholar
[35]	Demiray H, Abdikian A 2019 Chaos, Solitons Fractals 121 50 Google Scholar
[36]	Rasheed A, Murtaza G, Tsintsadze NL 2010 Phys. Rev. E 82 016403 Google Scholar
[37]	El-Shamy E, Al-Chouikh R, El-Depsy A, Al-Wadie N 2016 Phys. Plasmas 23 122122 Google Scholar
[38]	Cairns R A, Mamum A A, Bingham R, Boström R, Dendy R O, Nairn C M C, Shukla P K 1995 Geophys. Res. Lett. 22 2709 Google Scholar
[39]	Misra A P, Wang Y L 2015 Commun. Nonlinear Sci. Numer. Simul. 22 1360 Google Scholar
[40]	Pakzad H R, Tribeche M 2012 J. Fusion Energy 31 611 Google Scholar
[41]	El-Labany S K, El-Taibany W F, El-Bedwehy N A, Zedan N A 2017 Plasmas Phys. Rep. 43 756 Google Scholar
[42]	Nejoh Y 1992 IEEE Trans. Plasmas Sci. 20 80 Google Scholar
[43]	Saha A, Tamang J 2019 Adv. Space Res. 63 1596 Google Scholar
[44]	Saha A, Chatterjee P 2014 Astrophys. Space Sci. 350 631 Google Scholar

施引文献

图 1 色散关系随不同参数的变化规律

Fig. 1. Variations of dispersion relation with different parameters.

下载: 全尺寸图片幻灯片

图 2 系统相图随马赫数M的变化　(a) M = 1.3; (b) M = 1.4; (c) M = 1.5

Fig. 2. Variations of system phase diagram with different M: (a) M = 1.3; (b) M = 1.4; (c) M = 1.5.

下载: 全尺寸图片幻灯片

图 3 系统相图随nonthermal电子数$ \alpha $的变化　(a) α = 0; (b) α = 0.4; (c) α = 0.8

Fig. 3. Variations of system phase diagram with different $ \alpha $: (a) α = 0; (b) α = 0.4; (c) α = 0.8.

下载: 全尺寸图片幻灯片

图 4 系统相图随trapped离子数b的变化　(a) b = 0.7; (b) b = 0.8; (c) b = 0.9

Fig. 4. Variations of system phase diagram with different b: (a) b = 0.7; (b) b = 0.8; (c) b = 0.9.

下载: 全尺寸图片幻灯片

图 5 系统相图随参数$ {\sigma _{\mathrm{i}}} $的变化　(a) σ_i = 0.4; (b) σ_i = 0.5; (c) σ_i = 0.6

Fig. 5. Variations of system phase diagram with different $ {\sigma _{\mathrm{i}}} $: (a) σ_i = 0.4; (b) σ_i = 0.5; (c) σ_i = 0.6.

下载: 全尺寸图片幻灯片

图 6 系统相图随参数$ {\sigma _{\mathrm{d}}} $的变化　(a) σ_d = 0. 02; (b) σ_d = 0.05; (c) σ_d = 0.08

Fig. 6. Variations of system phase diagram with different $ {\sigma _{\mathrm{d}}} $: (a) σ_d = 0.02; (b) σ_d = 0.05; (c) σ_d = 0.08.

下载: 全尺寸图片幻灯片

图 7 系统相图随参数$ \delta $的变化　(a) δ = 2; (b) δ = 3; (c) δ = 4

Fig. 7. Variations of system phase diagram with different $ \delta $: (a) δ = 2; (b) δ = 3; (c) δ = 4.

下载: 全尺寸图片幻灯片

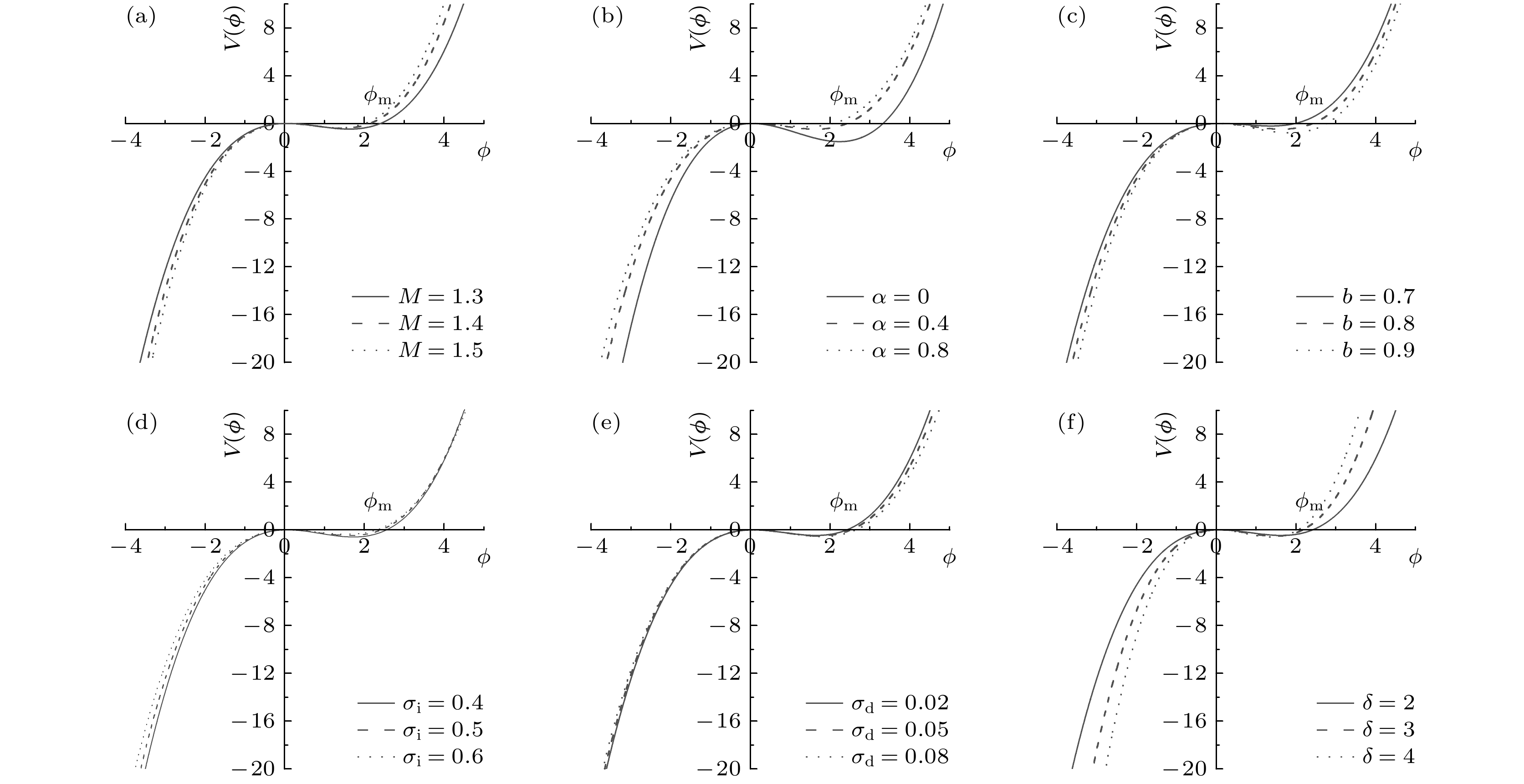
图 8 Sagdeev势函数$ V\left( \phi \right) $随不同系统参数的变化规律　(a) α = 0.4, b = 0.8, σ_i = 0.5, σ_d = 0.02, δ = 2; (b) M = 1.3, b = 0.8, σ_i = 0.5, σ_d = 0.02, δ = 2; (c) M = 1.3, α = 0.4, σ_i = 0.5, σ_d = 0.02, δ = 2; (d) M = 1.3, α = 0.4, b = 0.8, σ_d = 0.02, δ = 2; (e) M = 1.3, α = 0.4, b = 0.8, σ_i = 0.5, δ = 2; (f) M = 1.3, α = 0.4, b = 0.8, σ_i = 0.5, σ_d = 0.02

Fig. 8. Variations of Sagdeev potential $ V\left( \phi \right) $ with different parameters: (a) α = 0.4, b = 0.8, σ_i = 0.5, σ_d = 0.02, δ = 2; (b) M = 1.3, b = 0.8, σ_i = 0.5, σ_d = 0.02, δ = 2; (c) M = 1.3, α = 0.4, σ_i = 0.5, σ_d = 0.02, δ = 2; (d) M = 1.3, α = 0.4, b = 0.8, σ_d = 0.02, δ = 2; (e) M = 1.3, α = 0.4, b = 0.8, σ_i = 0.5, δ = 2; (f) M = 1.3, α = 0.4, b = 0.8, σ_i = 0.5, σ_d = 0.02.

下载: 全尺寸图片幻灯片

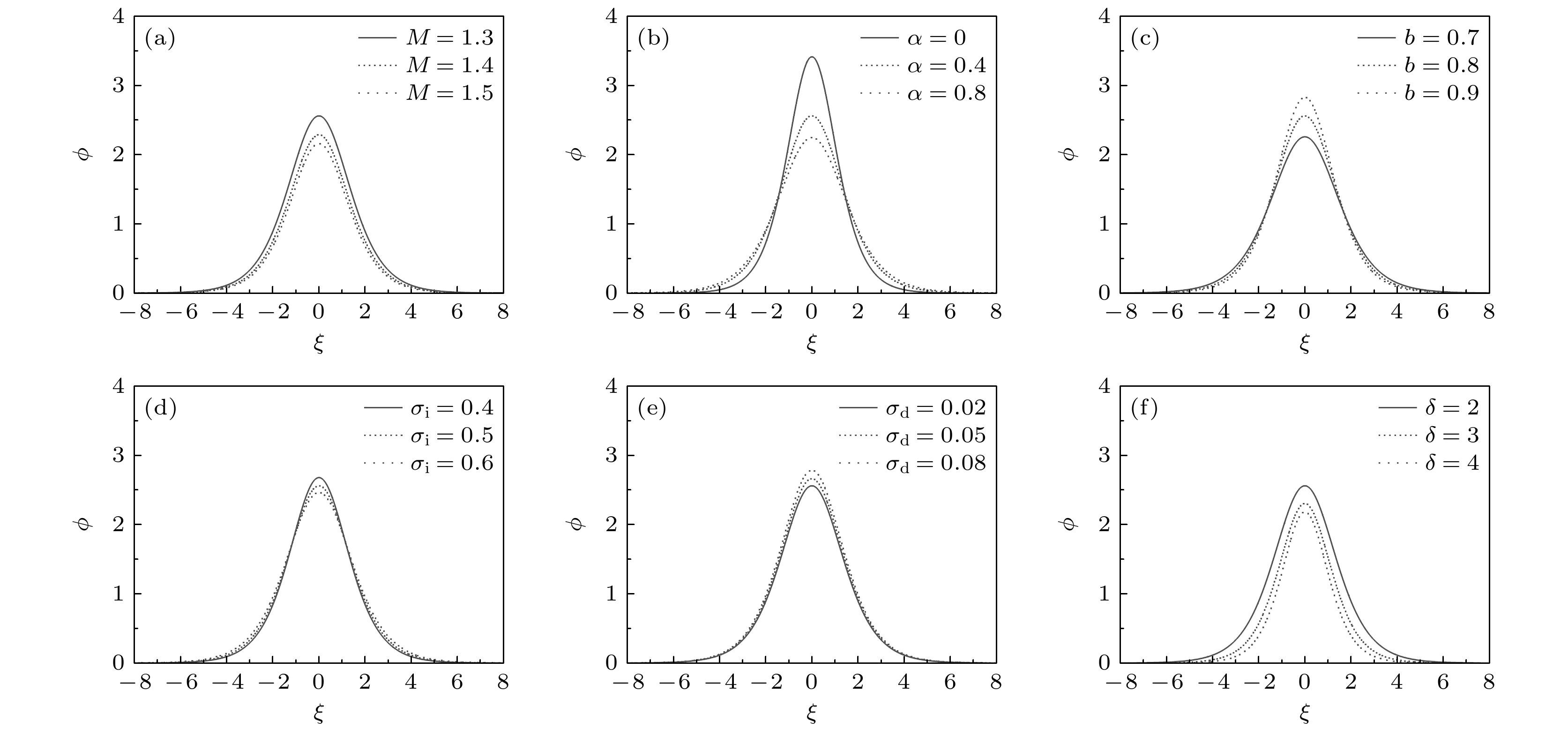
图 9 孤立波$ \phi $的波形随不同参数的变化规律　(a) α = 0.4, b = 0.8, σ_i = 0.5, σ_d = 0.02, δ = 2; (b) M = 1.3, b = 0.8, σ_i = 0.5, σ_d = 0.02, δ = 2; (c) M = 1.3, α = 0.4, σ_i = 0.5, σ_d = 0.02, δ = 2; (d) M = 1.3, α = 0.4, b = 0.8, σ_d = 0.02, δ = 2; (e) M = 1.3, α = 0.4, b = 0.8, σ_i = 0.5, δ = 2; (f) M = 1.3, α = 0.4, b = 0.8, σ_i = 0.5, σ_d = 0.02

Fig. 9. Waveform variations of the solitary waves $ \phi $ with different parameters: (a) α = 0.4, b = 0.8, σ_i = 0.5, σ_d = 0.02, δ = 2; (b) M = 1.3, b = 0.8, σ_i = 0.5, σ_d = 0.02, δ = 2; (c) M = 1.3, α = 0.4, σ_i = 0.5, σ_d = 0.02, δ = 2; (d) M = 1.3, α = 0.4, b = 0.8, σ_d = 0.02, δ = 2; (e) M = 1.3, α = 0.4, b = 0.8, σ_i = 0.5, δ = 2; (f) M = 1.3, α = 0.4, b = 0.8, σ_i = 0.5, σ_d = 0.02.

下载: 全尺寸图片幻灯片

map

[1]	Gill T S, Bains A S, Bedi C 2010 Phys. Plasmas. 17 013701 Google Scholar
[2]	Zahed H, Emadi E 2016 Phys. Plasmas. 23 083706 Google Scholar
[3]	Singh K, Kaur N, Saini N S 2017 Phys. Plasmas. 24 063703 Google Scholar
[4]	Akhter T, Mannan A, Mamun A A 2013 Plasma. Phys. Rep. 39 548 Google Scholar
[5]	Anowarm G M, Mamuna A 2008 Phys. Lett. 372 5896 Google Scholar
[6]	Rasheed A, Tsintsadze N L, Murtaza G 2011 Phys. Plasmas. 18 112701 Google Scholar
[7]	Rao N N, Shukla P K, Yu M Y 1990 Planet. Space. Sci. 38 543 Google Scholar
[8]	Barkan A, Merlino R L, N D Angelo 1995 Phys. Plasmas 2 3563 Google Scholar
[9]	Xie B S, He K F, Huang Z Q 1998 Chin. Phys. Lett. 15 892 Google Scholar
[10]	Lin M M, Duan W S 2005 Commun. Theor. Phys. 44 719 Google Scholar
[11]	Murad A, Zakir U, Haque Q 2019 Braz. J. Phys. 49 79 Google Scholar
[12]	Sarmah B, Devi A, Sarma J 2019 InfoKara 8 115 Google Scholar
[13]	Soni P K, Aravindakshan H, Kakad B, Kakad A 2021 Phys. Scr. 96 105604 Google Scholar
[14]	Jahan S, Banik S, Chowdhury N A, Mannan A, Mamun A A 2022 Gases 2 22 Google Scholar
[15]	林麦麦, 付颖捷, 宋秋影, 于腾萱, 文惠珊, 蒋蕾 2022 71 095203 Google Scholar Lin M M, Fu Y J, Song Q Y, Yu T X, Wen H S, Jiang L 2022 Acta Phys. Sin. 71 095203 Google Scholar
[16]	林麦麦, 王明月, 蒋蕾 2023 72 035201 Google Scholar Lin M M, Wang M Y, Jiang L 2023 Acta Phys. Sin. 72 035201 Google Scholar
[17]	Mamani C 2023 Braz. J. Phys. 53 110 Google Scholar
[18]	Saha T, Chatterjee P 2009 Phys. Plasmas 16 013707 Google Scholar
[19]	Mamun A A, Shukla P K 2009 Phys. Rev. E 80 037401 Google Scholar
[20]	Selim M M 2016 Eur. Phys. J. Plus 131 93 Google Scholar
[21]	Gill T S, Kaur H, Bansal S, Saini N S, Bala P 2007 Eur. Phys. J. D 41 151 Google Scholar
[22]	Mamun A A, Alam M N, Azad A K 1998 Phys. Plasmas 5 1212 Google Scholar
[23]	Mandal D, Lesur M, Gravier E, Sama J N, Guillevic A, Sarazin Y 2023 Plasma Phys. Controlled Fusion 65 055001 Google Scholar
[24]	Kaniadakis G, Lavagno A, Quarati P 1996 Phys. Lett. B 369 308 Google Scholar
[25]	El-Labany S K, El-Taibany W F, El-Abbasy O M 2007 Chaos, Solitons Fractals 33 813 Google Scholar
[26]	Salam M A, Akbar M A, Ali M Z 2021 Results Phys. 26 104376 Google Scholar
[27]	Kian R B, Mahdieh M H 2023 Fluid Dyn. Res. 55 35503 Google Scholar
[28]	Taylor H A, Daniell R E, Hartle R E, Brinton H C, Bauer S J, Scarf F L 1981 Adv. Space Res. 1 247 Google Scholar
[29]	Sabry R, Moslem W M, Shukla P K 2009 Phys. Plasmas 16 032302 Google Scholar
[30]	Amour R, Tribeche M 2010 Plasma Phys. 17 063702 Google Scholar
[31]	Haider M M, Ferdous T, Duha S S 2014 Cent. Eur. J. Phys. 12 701 Google Scholar
[32]	Ghai Y, Saini S N 2017 Astrophys. Space Sci. 362 3 Google Scholar
[33]	Annou K, Bahamida S, Annou R 2011 Pramana-J. Phys. 76 513 Google Scholar
[34]	Mamun A A 1998 Phys. Scr. 57 258 Google Scholar
[35]	Demiray H, Abdikian A 2019 Chaos, Solitons Fractals 121 50 Google Scholar
[36]	Rasheed A, Murtaza G, Tsintsadze NL 2010 Phys. Rev. E 82 016403 Google Scholar
[37]	El-Shamy E, Al-Chouikh R, El-Depsy A, Al-Wadie N 2016 Phys. Plasmas 23 122122 Google Scholar
[38]	Cairns R A, Mamum A A, Bingham R, Boström R, Dendy R O, Nairn C M C, Shukla P K 1995 Geophys. Res. Lett. 22 2709 Google Scholar
[39]	Misra A P, Wang Y L 2015 Commun. Nonlinear Sci. Numer. Simul. 22 1360 Google Scholar
[40]	Pakzad H R, Tribeche M 2012 J. Fusion Energy 31 611 Google Scholar
[41]	El-Labany S K, El-Taibany W F, El-Bedwehy N A, Zedan N A 2017 Plasmas Phys. Rep. 43 756 Google Scholar
[42]	Nejoh Y 1992 IEEE Trans. Plasmas Sci. 20 80 Google Scholar
[43]	Saha A, Tamang J 2019 Adv. Space Res. 63 1596 Google Scholar
[44]	Saha A, Chatterjee P 2014 Astrophys. Space Sci. 350 631 Google Scholar

[1]	林麦麦, 王明月, 蒋蕾. 多组分尘埃等离子体中非线性尘埃声孤波的传播特征. , 2023, 72(3): 035201. doi: 10.7498/aps.72.20221843
[2]	林麦麦, 付颖捷, 宋秋影, 于腾萱, 文惠珊, 蒋蕾. 热尘埃等离子体中(2 + 1)维尘埃声孤波的传播特征. , 2022, 71(9): 095203. doi: 10.7498/aps.71.20210902
[3]	欧阳成, 姚静荪, 石兰芳, 莫嘉琪. 一类尘埃等离子体孤波解. , 2014, 63(11): 110203. doi: 10.7498/aps.63.110203
[4]	莫嘉琪. 一类非线性尘埃等离子体孤波解. , 2011, 60(3): 030203. doi: 10.7498/aps.60.030203
[5]	仲生仁. 尘埃等离子体中非线性波的叠加效应及稳定性问题. , 2010, 59(4): 2178-2181. doi: 10.7498/aps.59.2178
[6]	贺兵香, 何济洲. 双势垒InAs/InP纳米线异质结热电子制冷机. , 2010, 59(6): 3846-3850. doi: 10.7498/aps.59.3846
[7]	李百文, 田恩科. 强激光与等离子体相互作用中受激陷俘电子声波散射及相空间离子涡旋的形成. , 2007, 56(8): 4749-4761. doi: 10.7498/aps.56.4749
[8]	郑志远, 李玉同, 远晓辉, 徐妙华, 梁文锡, 于全芝, 张翼, 王兆华, 魏志义, 张杰. 超热电子角分布和能谱的实验研究. , 2006, 55(10): 5349-5353. doi: 10.7498/aps.55.5349
[9]	谷渝秋, 蔡达锋, 郑志坚, 杨向东, 周维民, 焦春晔, 陈豪, 温天舒, 淳于书泰. 飞秒激光-固体靶相互作用中超热电子能量分布的实验研究. , 2005, 54(1): 186-191. doi: 10.7498/aps.54.186
[10]	彭晓昱, 张杰, 金展, 梁天骄, 仲佳勇, 武慧春, 刘运全, 王兆华, 陈正林, 盛政明, 李玉同, 魏志义. 超短脉冲激光与乙醇微滴相互作用中超热电子的双叶状角分布. , 2004, 53(8): 2625-2632. doi: 10.7498/aps.53.2625
[11]	徐桂琼, 李志斌. 构造非线性发展方程孤波解的混合指数方法. , 2002, 51(5): 946-950. doi: 10.7498/aps.51.946
[12]	陈正林, 张杰. 对超热电子诱生的磁场分布的估算. , 2001, 50(4): 735-740. doi: 10.7498/aps.50.735
[13]	吴衍青, 韩申生. 电子-离子碰撞对超热电子影响的PIC模拟计算. , 2000, 49(5): 915-921. doi: 10.7498/aps.49.915
[14]	陈正林, 张杰. 对超热电子诱生的磁场分布的估算. , 2000, 49(11): 2180-2185. doi: 10.7498/aps.49.2180
[15]	黄朝松, 吴颖. 热电子等离子体低频不稳定性的非线性理论. , 1990, 39(8): 61-68. doi: 10.7498/aps.39.61
[16]	关维恕, 王恩耀, 程仕清, 段淑云, 王纪海, 顾彪, 尚振奎. 电子迥旋加热等离子体及热电子环特性的实验研究. , 1989, 38(2): 228-235. doi: 10.7498/aps.38.228
[17]	黄朝松, 吴广学, 肖诗莉. 热电子等离子体无碰撞漂移波的稳定性. , 1989, 38(4): 629-636. doi: 10.7498/aps.38.629
[18]	马锦秀, 徐至展. 双束“自陷”激光驱动的电子等离子体波的拍频激发. , 1988, 37(5): 735-742. doi: 10.7498/aps.37.735
[19]	黄朝松, 邱励俭, 任兆杏. 热电子对低频等离子体漂移波的稳定作用. , 1988, 37(8): 1284-1290. doi: 10.7498/aps.37.1284
[20]	黄朝松, 任兆杏, 邱励俭. 热电子等离子体的耗散漂移不稳定性. , 1987, 36(9): 1112-1121. doi: 10.7498/aps.36.1112

计量

文章访问数: 2056
PDF下载量: 68
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

含有非热电子和陷俘离子的复杂等离子体中非线性尘埃声波的传播特征