三元Hf-C-N体系的空位有序结构及其力学性质和电子性质的第一性原理研究

彭军辉; TikhonovEvgenii

doi:10.7498/aps.70.20210244

摘要

采用第一性原理方法, 研究了三元Hf-C-N体系的空位有序结构及其力学性质和电子性质. 首先采用第一性原理和进化算法, 预测得到8种可能存在的热力学稳定的Hf-C-N空位有序结构; 这些结构都具有岩盐结构, 与实验发现的无序固溶体的结构类型一致. 本文的预测结果证明了Hf-C-N空位化合物能够以有序结构形式存在, 空位与C, N原子都位于[Hf₆]八面体间隙, 这一结构特点与HfC_x的相同. 然后采用第一性原理方法, 计算了Hf-C-N空位有序结构的力学性质, 发现除C∶N = 1∶4外, 相同C/N下, 随着空位浓度的增大, Hf-C-N的体模量、剪切模量、弹性模量、Pugh比、维氏硬度等降低; 而Hf₆CN₄ (空位浓度为1/6)的维氏硬度高于Hf₅CN₄ (无空位), 表现出空位硬化现象. 最后, 计算了Hf-C-N空位有序结构的态密度和晶体轨道哈密顿分布, 发现其具有强共价性和金属性; 且随着空位浓度增大, 总体键强减弱, 因而模量减小.

关键词:

Abstract

The thermal-mechanical properties of transition metal carbonitrides can be affected by the concentration and ordering of vacancies besides the C/N atomic ratio. However, there are few reports on the vacancy ordered structure of ternary transition metal carbonitrides. In the present paper, the first-principles method is used to study the vacancy ordered structures, mechanical properties, electronic properties and the effect of vacancies on the ternary Hf-C-N system. Firstly, the crystal structures of Hf-C-N system is examined by the first-principles and evolutionary algorithms implemented in USPEX under ambient pressure, and eight thermodynamical stable vacancy ordered structures are found, each of which has a rock-salt structure, and is also dynamical and mechanical stable, which are verified by the calculations of their phonon dispersion curves and elastic constants. The vacancies are occupied at the [Hf₆] octahedral interstices, which replace the positions of non-metal atoms. Their crystallographic data such as space group, lattice constants are also predicted. To the best of our knowledge, there is no report on the Hf-C-N vacancy ordered structures and these structures investigated here in this work are all found for the first time. Then their mechanical properties are calculated. The Hf-C-N vacancy ordered structures all have very high bulk, shear and elastic modulus and hardness. It is found that except for C∶N = 1∶4, for the Hf-C-N system with the same C/N ratio the moduli, Vickers hardness values, and Pugh’s ratios decrease with the increase of the concentration of vacancy. However, the Vickers hardness of Hf₆CN₄ (the concentration of vacancy is equal to 1/6) is higher than that of Hf₅CN₄ (no vacancy), that is so-called vacancy hardening. Finally, the electronic density of states and the crystal orbital Hamilton populations are calculated. The chemical bonding of Hf-C-N vacancy ordered structure is analyzed, which is a mixture of covalence and metallic and is similar to that of binary transition metal carbides and nitrides. With the increase of the concentration of vacancy, the total bond strength decreases, and then the modulus decreases for Hf-C-N compound.

Keywords:

作者及机构信息

彭军辉^1,2,
TikhonovEvgenii¹

1.
西北工业大学材料学院, 材料发现国际中心, 西安　710072

2.
太原工业学院材料工程系, 太原　030008

通信作者: TikhonovEvgenii, tikhonov.e@nwpu.edu.cn

基金项目: 外国人才引进与学术交流项目(批准号: B08040)资助的课题

Authors and contacts

1.
International Center for Materials Discovery, School of Materials Science and Engineering, Northwestern Polytechnical University, Xi’an 710072, China

2.
Department of Materials Engineering, Taiyuan Institute of Technology, Taiyuan 030008, China

Corresponding author: Tikhonov Evgenii, tikhonov.e@nwpu.edu.cn

Funds: Project supported by the Foreign Talents Introduction and Academic Exchange Program of China (Grant No. B08040)

文章全文 : translate this paragraph

参考文献

[1]	Squire T, Marschall J 2010 J. Eur. Ceram. Soc. 30 2239 Google Scholar
[2]	Opeka M M, Talmy I G, Zaykosk J A 2004 J. Mater. Sci. 39 5887 Google Scholar
[3]	Levine S R, Opila E J, Halbig M C, Kiser J D, Singh M, Salem J A 2002 J. Eur. Ceram. Soc. 22 2757 Google Scholar
[4]	Ushakov SV, Navrotsky A 2012 J. Am. Ceram. Soc. 95 1463 Google Scholar
[5]	Grill A, Aron P R 1983 Thin Solid Films 108 173 Google Scholar
[6]	Helmersson U, Todorova S, Barnett S A, Sundgren J E, Markert L C, Greene J E 1987 J. Appl. Phys. 62 481 Google Scholar
[7]	Mirkarimi P B, Hultman L, Barnett S A 1990 Appl. Phys. Lett. 57 2654 Google Scholar
[8]	Veprek S, Veprek-Heijman M G J, Karvankova P, Prochazka J 2005 Thin Solid Films 476 1 Google Scholar
[9]	Hultman L, Bareno J, Flink A, Soderberg H, Larsson K, Petrova V, Oden M, Greene J E, Petrov I 2007 Phys. Rev. B 75 155437 Google Scholar
[10]	Shin C S, Gall D, Hellgren N, Patscheider J, Petrov I, Greene J E 2003 J. Appl. Phys. 93 6025 Google Scholar
[11]	Jhi S H, Louie S G, Cohen M L, Ihm J 2001 Phys. Rev. Lett. 86 3348 Google Scholar
[12]	Shin C S, Rudenja S, Gall D, Hellgren N, Lee T Y, Petrov I, Greene J E 2004 J. Appl. Phys. 95 356 Google Scholar
[13]	Lee T, Ohmori K, Shin C S, Cahill D G, Petrov I, Greene J E 2005 Phys. Rev. B 71 144106 Google Scholar
[14]	Holleck H 1986 J. Vac. Sci. Technol., A 4 2661 Google Scholar
[15]	Yang Q, Lengauer W, Koch T, Scheerer M, Smid I 2000 J. Alloys Compd. 309 L5 Google Scholar
[16]	Jhi S H, Ihm J, Louie S G, Cohen M L 1999 Nature 399 132 Google Scholar
[17]	Feng W, Cui S, Hu H, Zhang G, Lü Z 2011 Physica B 406 3631 Google Scholar
[18]	Balasubramanian K, Khare S V, Gall D 2018 Acta Mater. 152 175 Google Scholar
[19]	Peng J, Tikhonov E 2021 Comput. Mater. Sci. 195 110464 Google Scholar
[20]	Gusev A I, Rempel A A, Magerl A J 2001 Disorder and Order in Strongly Nonstoichiometric Compounds (Berlin Heidelberg: Springer) pp179−243
[21]	Gusev A I 1991 Physical Chemistry of Non stoichiometric Refractory Compounds (Moscow: Nauka) (in Russian)
[22]	Rudy E 1965 Ternary Phase Equilibria in Transition Metal-boron-carbon-silicon Systems. Part II. Ternary Systems. Vol. I. Ta-Hf-C system (Air Force Materials Laboratory, Wright-Patterson Air Force Base) pp38−60
[23]	Lipatnikov V N, Lengauer W, Ettmayer P, Keil E, Groboth G, Kny E 1997 J. Alloys Compd. 261 192 Google Scholar
[24]	Yu X X, Thompson G B, Weinberger C R 2015 J. Eur. Ceram. Soc. 35 95 Google Scholar
[25]	Yu X X, Weinberger C R, Thompson G B 2016 Comput. Mater. Sci. 112 318 Google Scholar
[26]	Yu X X, Weinberger C R, Thompson G B 2014 Acta Mater. 80 341 Google Scholar
[27]	Xie C, Liu N, Cheng X, Li D, Zeng Q 2016 J. Eur. Ceram. Soc. 36 3593 Google Scholar
[28]	Xie C, Oganov A R, Li D, Debela T T, Liu N, Dong D, Zeng Q 2016 Phys. Chem. Chem. Phys. 18 12299 Google Scholar
[29]	Zhang Y, Liu B, Wang J 2016 Sci. Rep. 5 18098 Google Scholar
[30]	Gunda N S H, Van der Ven A 2018 Phys. Rev. Mater. 2 083602 Google Scholar
[31]	Connolly J W D, Williams A R 1983 Phy. Rev. B 27 5169 Google Scholar
[32]	Weinberger C R, Thompson G B 2018 J. Am. Ceram. Soc. 101 4401 Google Scholar
[33]	Gusev A I, Rempel A A 1994 J. Phys. Chem. Solids 55 299 Google Scholar
[34]	Yu S, Zeng Q, Oganov A R, Frapper G, Zhang L 2015 Phys. Chem. Chem. Phys. 17 11763 Google Scholar
[35]	Yu S, Zeng Q, Oganov A R, Frapper G, Huang B, Niu H, Zhang L 2017 RSC Adv. 7 4697 Google Scholar
[36]	樊涛, 曾庆丰, 于树印 2016 65 118102 Google Scholar Fan T, Zeng Q F, Yu S Y 2016 Acta Phys. Sin. 65 118102 Google Scholar
[37]	Zhao Z L, Bao K, Tian F B, Duan D F, Liu B B, Cui T 2015 Phys. Chem. Chem. Phys. 17 22837 Google Scholar
[38]	Li D, Tian F B, Duan D F, Bao K, Chu B, Sha X, Liu B B, Cui T 2014 RSC Adv. 4 10133 Google Scholar
[39]	Oganov A R, Glass C W 2006 J. Chem. Phys. 124 244704 Google Scholar
[40]	Lyakhov A O, Oganov A R, Stokes H T, Zhu Q 2013 Comput. Phys. Commun. 184 1172 Google Scholar
[41]	Oganov A R, Lyakhov A O, Valle M 2011 Acc. Chem. Res. 44 227 Google Scholar
[42]	Rudy E 1970 J. Less-Common Met. 20 49 Google Scholar
[43]	Erniraliev A, Karimov I, Faizullaev F, Patiev M 1978 Kristallografiya 33 778
[44]	Karimov I, Em V T, Petrunin V F, Latergaus I S, Polishuk V S 1976 Materialy 12 1492
[45]	Em V T, Karimov I, Latergaus I S 1987 Metallofizika 9 113
[46]	Em V T, Tashmetov M Y 1996 Phys. Status Solidi B 198 571 Google Scholar
[47]	Binder S, Lengauer W, Ettmayer P, Bauer J, Debuigne J, Bohn M 1995 J. Alloys Compd. 217 128 Google Scholar
[48]	Hong Q J, van de Walle A 2015 Phys. Rev. B 92 020104 Google Scholar
[49]	Buinevich V S, Nepapushev A A, Moskovskikh D O, Trusov G V, Kuskov K V, Vadchenko S G, Rogachev A S, Mukasyan A S 2020 Ceram. Int. 46 16068 Google Scholar
[50]	Oganov A R 2011 Modern methods of crystal structure prediction (Weinheim: Wiley-VCR)
[51]	Kresse G, Furthmüller J 1996 Phys. Rev. B:Condens. Matter 54 11169 Google Scholar
[52]	Blöchl P E 1994 Phys. Rev. B:Condens. Matter 50 17953 Google Scholar
[53]	Perdew J P, Ruzsinszky A, Csonka G I, Vydrov O A, Scuseria G E, Constantin L A, Zhou X, Burke K 2008 Phys. Rev. Lett. 100 136406 Google Scholar
[54]	Voigt W 1928 Lehrbuch der Kristallphysik (Leipzig, Germany: B. G. Teubner)
[55]	Reuss A 1929 Z. Angew. Math. Mech. 9 49 Google Scholar
[56]	Hill R W 1952 Proc. Phys. Soc. London, Sect. A 65 349 Google Scholar
[57]	Chen X Q, Niu H, Li D, Li Y 2011 Intermetallics 19 1275 Google Scholar
[58]	Pugh S F 1954 Philos. Mag. 45 823 Google Scholar
[59]	Togo A, Oba F, Tanaka I 2008 Phys. Rev. B 78 134106 Google Scholar
[60]	Momma K, Izumi F 2011 J. Appl. Crystallogr. 44 1272 Google Scholar
[61]	Dronskowski R, Bloechl P E 1993 J. Phys. Chem. 97 8617 Google Scholar
[62]	Hinuma Y, Pizzi G, Kumagai Y, Oba F, Tanaka I 2017 Comput. Mater. Sci. 128 140 Google Scholar
[63]	Cowley R A 1976 Phys. Rev. B 13 4877 Google Scholar

施引文献

图 1 (a) 常压下, 三元Hf-HfC-HfN体系的能量凸包图, 黑色球表示热力学稳定结构, 其他为亚稳结构; (b) Hf-C-N空位有序结构的X射线衍射模拟图谱, 衍射源为Cu Kα射线

Fig. 1. (a) Enthalpy convex-hull of ternary Hf-HfC-HfN system at ambient pressure. The black sphere indicates stable structure, and others are metastable structure. (b) The simulated X-ray diffractions of Hf-C-N vacancy ordered structures with a copper Kα X-ray source.

下载: 全尺寸图片幻灯片

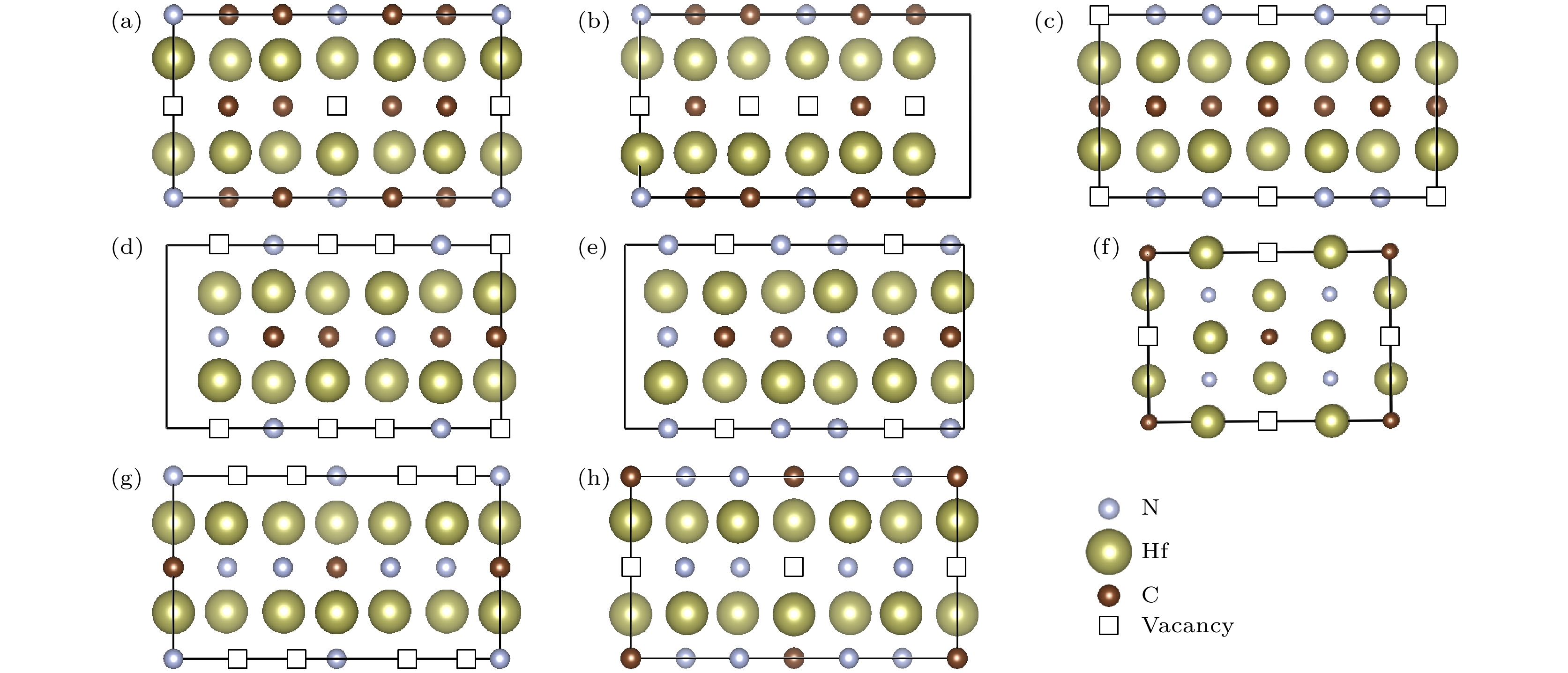
图 2 Hf-C-N空位有序结构在某一晶面上的空位分布　(a) Hf₆C₄N-$C2 $/m (0 0 1); (b) Hf₆C₃N-$C2 $ (1 0 0); (c) Hf₆C₃N₂-$C2 $/m (1 0 0); (d) Hf₃CN-$C2 $ (1 0 0); (e) Hf₆C₂N₃-$C2 $ (1 0 0); (f) Hf₄CN₂-Cmmm (0 0 1); (g) Hf₆CN₃-$C2 $/m (1 0 0); (h) Hf₆CN₄-$C2 $/m (0 0 1)

Fig. 2. Vacancies on the crystallographic plane: (a) Hf₆C₄N-$C2 $/m (0 0 1); (b) Hf₆C₃N-$C2 $ (1 0 0); (c) Hf₆C₃N₂-$C2 $/m (1 0 0); (d) Hf₃CN-$C2 $ (1 0 0); (e) Hf₆C₂N₃-$C2 $ (1 0 0); (f) Hf₄CN₂-Cmmm (0 0 1); (g) Hf₆CN₃-$C2 $/m (1 0 0); (h) Hf₆CN₄-$C2 $/m (0 0 1).

下载: 全尺寸图片幻灯片

图 3 Hf-C-N空位有序结构的声子谱曲线　(a) Hf₆C₄N-$C2 $/m; (b) Hf₆C₃N-$C2 $; (c) Hf₆C₃N₂-$C2 $/m; (d) Hf₃CN-$C2 $; (e) Hf₆C₂N₃-$C2 $; (f) Hf₄CN₂-Cmmm; (g) Hf₆CN₃-$C2 $/m; (h) Hf₆CN₄-$C2 $/m

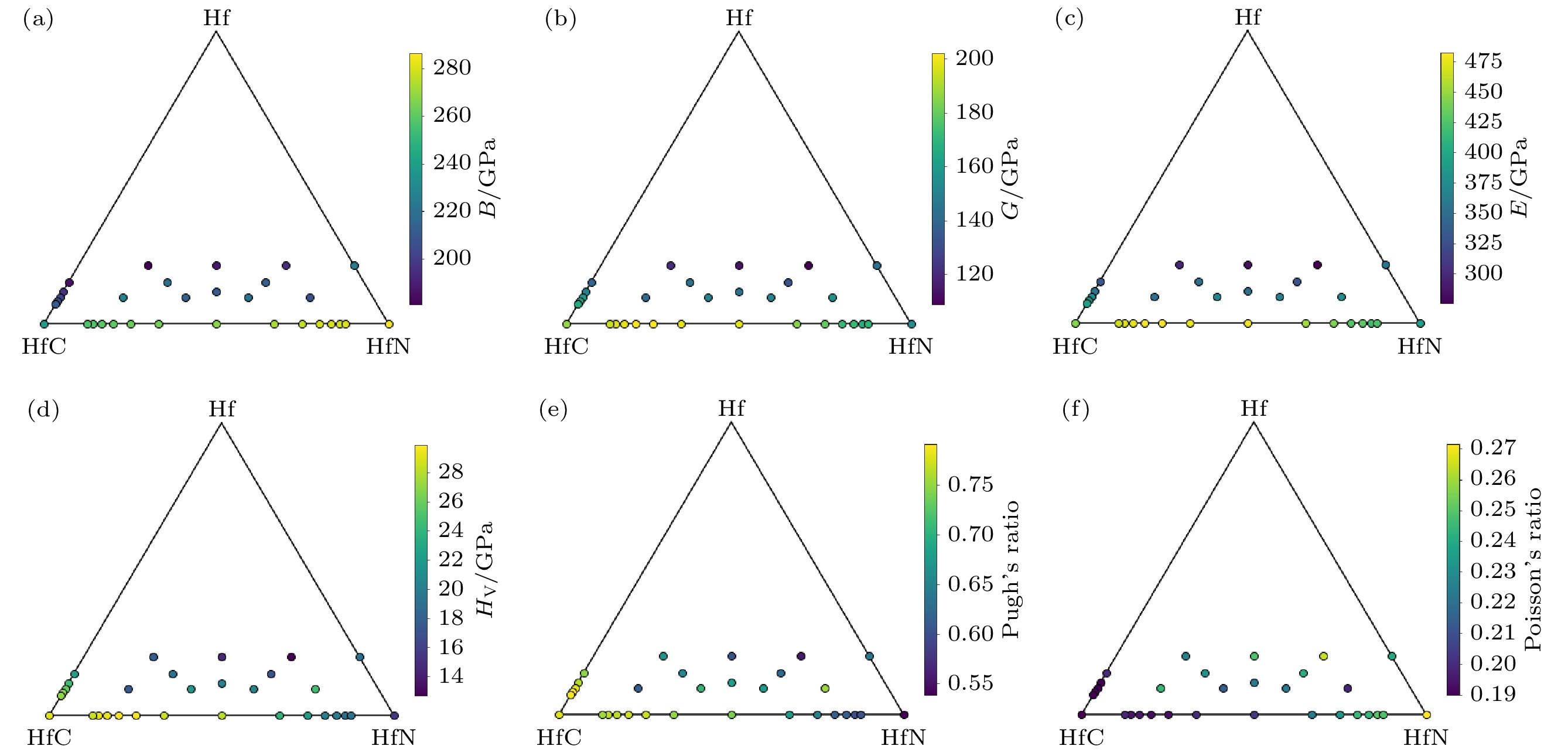
Fig. 3. Phonon dispersion curves of (a) Hf₆C₄N-$C2 $/m, (b) Hf₆C₃N-$C2 $, (c) Hf₆C₃N₂-$C2 $/m, (d) Hf₃CN-$C2 $, (e) Hf₆C₂N₃-$C2 $, (f) Hf₄CN₂-Cmmm, (g) Hf₆CN₃-$C2 $/m, (h) Hf₆CN₄-$C2 $/m. They are all dynamical stable because no imaginary frequencies were found in Brillouin zone.

下载: 全尺寸图片幻灯片

图 4 三元Hf-HfC-HfN体系的力学性质-组分相图　(a) 体模量(B); (b) 剪切模量(G ); (c) 弹性模量(E ); (d) 维氏硬度(H_V); (e) Pugh比(G/B); (f) 泊松比(μ)

Fig. 4. Mechanical properties-composition diagrams of ternary Hf-HfC-HfN system: (a) Bulk modulus (B); (b) shear modulus (G ); (c) elastic modulus (E ); (d) Vickers hardness (H_V); (e) Pugh’s ratio (G/B); (f) Poisson’s ratio (μ).

下载: 全尺寸图片幻灯片

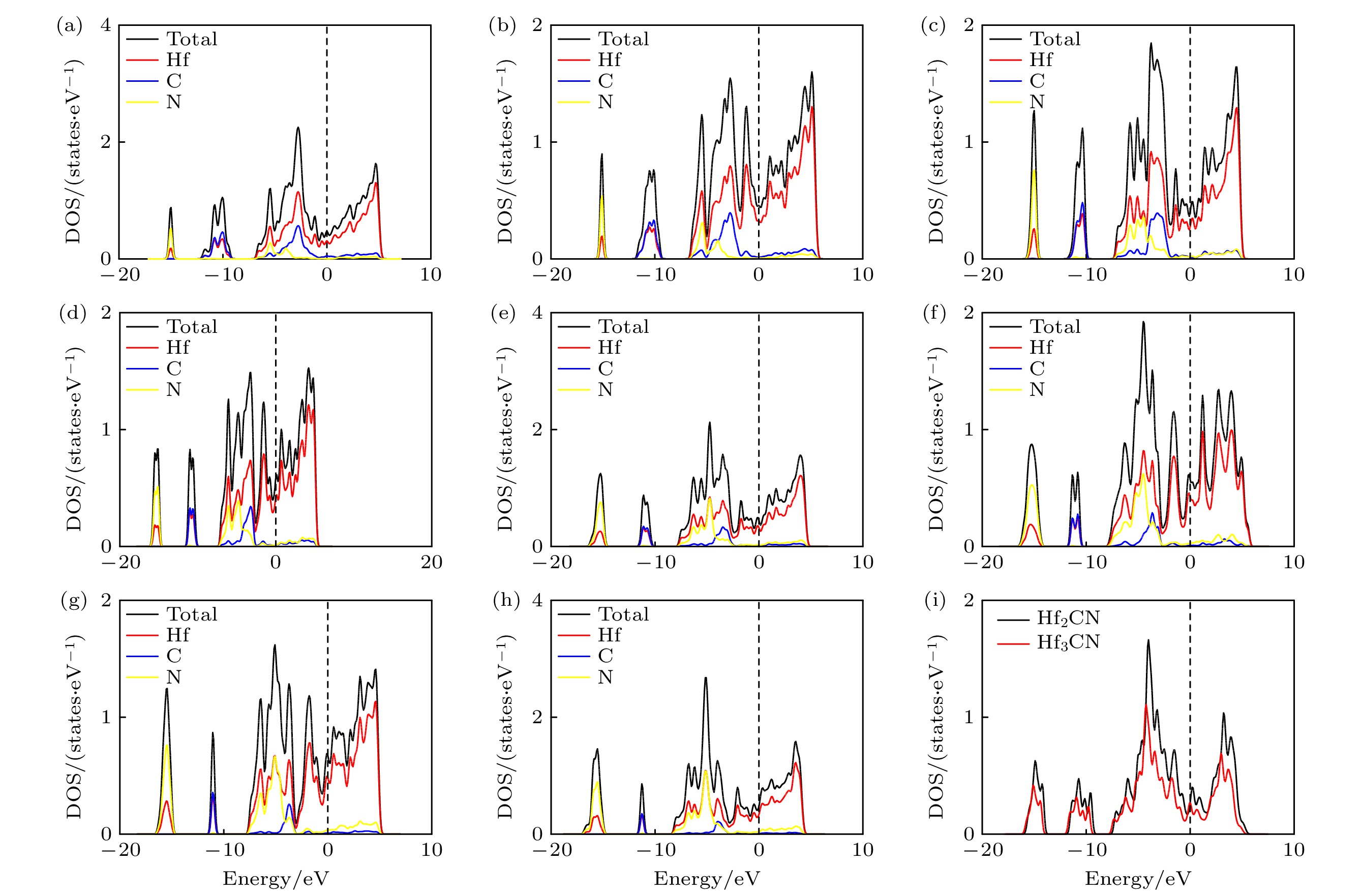
图 5 (a) Hf₆C₄N-$C2 $/m, (b) Hf₆C₃N-$C2 $, (c) Hf₆C₃N₂-$C2 $/m, (d) Hf₃CN-$C2 $, (e) Hf₆C₂N₃-$C2 $, (f) Hf₄CN₂-Cmmm, (g) Hf₆CN₃-$C2 $/m和(h) Hf₆CN₄-$C2 $/m的态密度和分态密度; (i) Hf₃CN和Hf₂CN的总态密度对比; 其中Fermi能级位于0 eV

Fig. 5. Density of state (DOS) and partial density of state (PDOS) normalized by per HfC_xN_y of (a) Hf₆C₄N-$C2 $/m, (b) Hf₆C₃N-$C2 $, (c) Hf₆C₃N₂-$C2 $/m, (d) Hf₃CN-$C2 $, (e) Hf₆C₂N₃-$C2 $, (f) Hf₄CN₂-Cmmm, (g) Hf₆CN₃-$C2 $/m and (h) Hf₆CN₄-$C2 $/m; (i) the total DOS of Hf₃CN and Hf₂CN normalized by per HfC_xN_y. The Fermi level is at 0 eV.

下载: 全尺寸图片幻灯片

图 6 Hf-C-N化合物的晶体轨道哈密顿分布(–COHP), Fermi能级位于0 eV

Fig. 6. Crystal orbital Hamilton populations (–COHP) of Hf-C-N compounds. The Fermi level is at 0 eV.

下载: 全尺寸图片幻灯片

表 1 Hf-C-N空位有序结构的空间群、晶格常数、反应焓ΔH (eV/atom)、Hf原子的配位数(CN) 和空位浓度(CV)

Table 1. Space group, lattice constants, the enthalpy of reaction ΔH (eV/atom), coordination number (CN) of Hf and the concentration of vacancy (CV) of Hf-C-N vacancy ordered structures.

Compound	Space group	Lattice constants/Å	ΔH/(eV·atom^–1)	CN	CV
Hf₆C₄N	$C2 $/m	a = 5.679, b = 9.799, c = 5.671, β = 70.6^o	–0.0899	5	1/6
Hf₆C₃N	$C2 $	a = 5.658, b = 9.763, c = 9.262, β = 144.8^o	–0.0980	4	1/3
Hf₆C₃N₂	$C2 $m	a = 5.660, b = 9.783, c = 5.619, β = 109.6^o	–0.1038	5	1/6
Hf₃CN	$C2 $	a = 5.632, b = 9.705, c = 5.625, β = 109.8^o	–0.1107	4	1/3
Hf₆C₂N₃	$C2 $	a = 5.624, b = 9.725, c = 5.602, β = 109.6^o	–0.1047	5	1/6
Hf₄CN₂	Cmmm	a = 6.427, b = 9.147, c = 3.235	–0.1082	4/5	1/4
Hf₆CN₃	$C2 $/m	a = 5.592, b = 9.658, c = 6.455, β = 125.3^o	–0.0894	4	1/3
Hf₆CN₄	$C2 $/m	a = 5.580, b = 9.681, c = 5.587, β = 70.3^o	–0.0815	5	1/6

下载: 导出CSV

表 2 Hf-C-N空位有序结构的弹性常数C_ij (单位: GPa)

Table 2. Calculated elastic constants C_ij (in GPa) of Hf-C-N vacancy ordered structures.

Compounds	C₁₁	C₂₂	C₃₃	C₄₄	C₅₅	C₆₆	C₁₂	C₁₃	C₂₃
Hf₆C₄N-$C2 $/m	414.3	406.6	415.6	158.0	170.6	148.7	94.1	116.1	104.5
Hf₆C₃N-$C2 $	358.5	362.8	352.2	100.0	114.3	132.3	87.5	98.3	91.6
Hf₆C₃N₂-$C2 $/m	414.6	417.4	407.6	152.2	157.6	147.8	111.9	115.0	116.3
Hf₃CN-$C2 $	354.5	363.5	348.7	90.6	103.6	128.7	102.1	109.5	101.3
Hf₆C₂N₃-$C2 $	409.7	418.7	418.1	149.6	160.2	148.9	123.4	122.9	126.5
Hf₄CN₂-Cmmm	373.4	368.8	406.8	142.2	133.1	135.8	146.4	112.0	124.4
Hf₆CN₃-$C2 $/m	361.1	358.4	351.7	84.9	99.8	124.9	108.1	121.7	114.2
Hf₆CN₄-$C2 $/m	401.2	414.1	403.5	146.5	157.2	139.8	134.0	139.9	147.8

下载: 导出CSV

表 3 Hf-C-N空位有序结构和HfC_1–xN_x^[19]的力学性质—体模量(B)、剪切模量(G )、弹性模量(E )、泊松比(μ)、Pugh比(G/B)、维氏硬度(H_V)等

Table 3. Mechanical properties—bulk modulus (B), shear modulus (G ), elastic modulus (E ), Poisson’s ratio (μ), Pugh’s ratio (G/B), Vickers hardness (H_V) of Hf-C-N vacancy ordered structures and HfC_1–xN_x^[19].

Compound	B /GPa	G /GPa	E /GPa	μ	G/B	H_V /GPa
Hf₆C₄N	229.0	140.8	350.6	0.2449	0.6148	17.5
Hf₅C₄N^[19]	260.6	201.3	480.3	0.1928	0.7727	29.9
Hf₆C₃N	180.9	121.5	297.9	0.2256	0.6717	17.8
Hf₄C₃N^[19]	262.2	202.1	482.4	0.1934	0.7707	29.9
Hf₆C₃N₂	214.0	151.1	366.9	0.2143	0.7059	22.1
Hf₃CN	188.0	113.4	283.3	0.2489	0.6031	14.6
Hf₂CN^[19]	268.1	198.5	477.6	0.2031	0.7403	28.1
Hf₆C₂N₃	221.3	149.7	366.6	0.2239	0.6766	20.7
Hf₄CN₂	212.7	132.8	329.7	0.2417	0.6242	17.1
Hf₃CN₂^[19]	272.8	185.1	452.8	0.2233	0.6786	23.9
Hf₆CN₃	195.4	108.9	275.6	0.2650	0.5574	12.7
Hf₄CN₃^[19]	276.2	179.6	442.8	0.2328	0.6504	22.2
Hf₆CN₄	207.2	156.1	374.4	0.1989	0.7535	24.6
Hf₅CN₄^[19]	279.0	171.5	427.0	0.2449	0.6147	20.0

下载: 导出CSV

表 4 Hf-C-N化合物的晶体轨道哈密顿分布的积分值(–ICOHP)

Table 4. Integrated crystal orbital Hamilton populations (–ICOHP) of Hf-C-N compounds.

Compound	–ICOHP			Compound	–ICOHP
Compound	Hf—C	Hf—N	Hf—Hf	Compound	Hf—C	Hf—N	Hf—Hf
Hf₆C₄N	3.373	3.567	0.529	Hf₆C₃N₂	3.181	2.990	0.571
Hf₅C₄N	3.373	3.033	0.459	Hf₄CN₂	3.474	3.111	0.650
Hf₆C₃N	3.350	3.067	0.718	Hf₃CN₂	3.551	3.091	0.541
Hf₄C₃N	3.319	3.029	0.454	Hf₆CN₃	3.408	3.211	0.570
Hf₆C₃N₂	3.607	3.103	0.530	Hf₄CN₃	3.321	3.159	0.520
Hf₃CN	3.277	3.211	0.737	Hf₆CN₄	3.675	3.179	0.591
Hf₂CN	3.483	2.802	0.490	Hf₅CN₄	3.319	3.017	0.500

下载: 导出CSV

map

[1]	Squire T, Marschall J 2010 J. Eur. Ceram. Soc. 30 2239 Google Scholar
[2]	Opeka M M, Talmy I G, Zaykosk J A 2004 J. Mater. Sci. 39 5887 Google Scholar
[3]	Levine S R, Opila E J, Halbig M C, Kiser J D, Singh M, Salem J A 2002 J. Eur. Ceram. Soc. 22 2757 Google Scholar
[4]	Ushakov SV, Navrotsky A 2012 J. Am. Ceram. Soc. 95 1463 Google Scholar
[5]	Grill A, Aron P R 1983 Thin Solid Films 108 173 Google Scholar
[6]	Helmersson U, Todorova S, Barnett S A, Sundgren J E, Markert L C, Greene J E 1987 J. Appl. Phys. 62 481 Google Scholar
[7]	Mirkarimi P B, Hultman L, Barnett S A 1990 Appl. Phys. Lett. 57 2654 Google Scholar
[8]	Veprek S, Veprek-Heijman M G J, Karvankova P, Prochazka J 2005 Thin Solid Films 476 1 Google Scholar
[9]	Hultman L, Bareno J, Flink A, Soderberg H, Larsson K, Petrova V, Oden M, Greene J E, Petrov I 2007 Phys. Rev. B 75 155437 Google Scholar
[10]	Shin C S, Gall D, Hellgren N, Patscheider J, Petrov I, Greene J E 2003 J. Appl. Phys. 93 6025 Google Scholar
[11]	Jhi S H, Louie S G, Cohen M L, Ihm J 2001 Phys. Rev. Lett. 86 3348 Google Scholar
[12]	Shin C S, Rudenja S, Gall D, Hellgren N, Lee T Y, Petrov I, Greene J E 2004 J. Appl. Phys. 95 356 Google Scholar
[13]	Lee T, Ohmori K, Shin C S, Cahill D G, Petrov I, Greene J E 2005 Phys. Rev. B 71 144106 Google Scholar
[14]	Holleck H 1986 J. Vac. Sci. Technol., A 4 2661 Google Scholar
[15]	Yang Q, Lengauer W, Koch T, Scheerer M, Smid I 2000 J. Alloys Compd. 309 L5 Google Scholar
[16]	Jhi S H, Ihm J, Louie S G, Cohen M L 1999 Nature 399 132 Google Scholar
[17]	Feng W, Cui S, Hu H, Zhang G, Lü Z 2011 Physica B 406 3631 Google Scholar
[18]	Balasubramanian K, Khare S V, Gall D 2018 Acta Mater. 152 175 Google Scholar
[19]	Peng J, Tikhonov E 2021 Comput. Mater. Sci. 195 110464 Google Scholar
[20]	Gusev A I, Rempel A A, Magerl A J 2001 Disorder and Order in Strongly Nonstoichiometric Compounds (Berlin Heidelberg: Springer) pp179−243
[21]	Gusev A I 1991 Physical Chemistry of Non stoichiometric Refractory Compounds (Moscow: Nauka) (in Russian)
[22]	Rudy E 1965 Ternary Phase Equilibria in Transition Metal-boron-carbon-silicon Systems. Part II. Ternary Systems. Vol. I. Ta-Hf-C system (Air Force Materials Laboratory, Wright-Patterson Air Force Base) pp38−60
[23]	Lipatnikov V N, Lengauer W, Ettmayer P, Keil E, Groboth G, Kny E 1997 J. Alloys Compd. 261 192 Google Scholar
[24]	Yu X X, Thompson G B, Weinberger C R 2015 J. Eur. Ceram. Soc. 35 95 Google Scholar
[25]	Yu X X, Weinberger C R, Thompson G B 2016 Comput. Mater. Sci. 112 318 Google Scholar
[26]	Yu X X, Weinberger C R, Thompson G B 2014 Acta Mater. 80 341 Google Scholar
[27]	Xie C, Liu N, Cheng X, Li D, Zeng Q 2016 J. Eur. Ceram. Soc. 36 3593 Google Scholar
[28]	Xie C, Oganov A R, Li D, Debela T T, Liu N, Dong D, Zeng Q 2016 Phys. Chem. Chem. Phys. 18 12299 Google Scholar
[29]	Zhang Y, Liu B, Wang J 2016 Sci. Rep. 5 18098 Google Scholar
[30]	Gunda N S H, Van der Ven A 2018 Phys. Rev. Mater. 2 083602 Google Scholar
[31]	Connolly J W D, Williams A R 1983 Phy. Rev. B 27 5169 Google Scholar
[32]	Weinberger C R, Thompson G B 2018 J. Am. Ceram. Soc. 101 4401 Google Scholar
[33]	Gusev A I, Rempel A A 1994 J. Phys. Chem. Solids 55 299 Google Scholar
[34]	Yu S, Zeng Q, Oganov A R, Frapper G, Zhang L 2015 Phys. Chem. Chem. Phys. 17 11763 Google Scholar
[35]	Yu S, Zeng Q, Oganov A R, Frapper G, Huang B, Niu H, Zhang L 2017 RSC Adv. 7 4697 Google Scholar
[36]	樊涛, 曾庆丰, 于树印 2016 65 118102 Google Scholar Fan T, Zeng Q F, Yu S Y 2016 Acta Phys. Sin. 65 118102 Google Scholar
[37]	Zhao Z L, Bao K, Tian F B, Duan D F, Liu B B, Cui T 2015 Phys. Chem. Chem. Phys. 17 22837 Google Scholar
[38]	Li D, Tian F B, Duan D F, Bao K, Chu B, Sha X, Liu B B, Cui T 2014 RSC Adv. 4 10133 Google Scholar
[39]	Oganov A R, Glass C W 2006 J. Chem. Phys. 124 244704 Google Scholar
[40]	Lyakhov A O, Oganov A R, Stokes H T, Zhu Q 2013 Comput. Phys. Commun. 184 1172 Google Scholar
[41]	Oganov A R, Lyakhov A O, Valle M 2011 Acc. Chem. Res. 44 227 Google Scholar
[42]	Rudy E 1970 J. Less-Common Met. 20 49 Google Scholar
[43]	Erniraliev A, Karimov I, Faizullaev F, Patiev M 1978 Kristallografiya 33 778
[44]	Karimov I, Em V T, Petrunin V F, Latergaus I S, Polishuk V S 1976 Materialy 12 1492
[45]	Em V T, Karimov I, Latergaus I S 1987 Metallofizika 9 113
[46]	Em V T, Tashmetov M Y 1996 Phys. Status Solidi B 198 571 Google Scholar
[47]	Binder S, Lengauer W, Ettmayer P, Bauer J, Debuigne J, Bohn M 1995 J. Alloys Compd. 217 128 Google Scholar
[48]	Hong Q J, van de Walle A 2015 Phys. Rev. B 92 020104 Google Scholar
[49]	Buinevich V S, Nepapushev A A, Moskovskikh D O, Trusov G V, Kuskov K V, Vadchenko S G, Rogachev A S, Mukasyan A S 2020 Ceram. Int. 46 16068 Google Scholar
[50]	Oganov A R 2011 Modern methods of crystal structure prediction (Weinheim: Wiley-VCR)
[51]	Kresse G, Furthmüller J 1996 Phys. Rev. B:Condens. Matter 54 11169 Google Scholar
[52]	Blöchl P E 1994 Phys. Rev. B:Condens. Matter 50 17953 Google Scholar
[53]	Perdew J P, Ruzsinszky A, Csonka G I, Vydrov O A, Scuseria G E, Constantin L A, Zhou X, Burke K 2008 Phys. Rev. Lett. 100 136406 Google Scholar
[54]	Voigt W 1928 Lehrbuch der Kristallphysik (Leipzig, Germany: B. G. Teubner)
[55]	Reuss A 1929 Z. Angew. Math. Mech. 9 49 Google Scholar
[56]	Hill R W 1952 Proc. Phys. Soc. London, Sect. A 65 349 Google Scholar
[57]	Chen X Q, Niu H, Li D, Li Y 2011 Intermetallics 19 1275 Google Scholar
[58]	Pugh S F 1954 Philos. Mag. 45 823 Google Scholar
[59]	Togo A, Oba F, Tanaka I 2008 Phys. Rev. B 78 134106 Google Scholar
[60]	Momma K, Izumi F 2011 J. Appl. Crystallogr. 44 1272 Google Scholar
[61]	Dronskowski R, Bloechl P E 1993 J. Phys. Chem. 97 8617 Google Scholar
[62]	Hinuma Y, Pizzi G, Kumagai Y, Oba F, Tanaka I 2017 Comput. Mater. Sci. 128 140 Google Scholar
[63]	Cowley R A 1976 Phys. Rev. B 13 4877 Google Scholar

[1]	计晨. 原子兰姆位移与超精细结构中的核结构效应. , 2024, 73(20): 202101. doi: 10.7498/aps.73.20241063
[2]	崔子纯, 杨莫涵, 阮晓鹏, 范晓丽, 周峰, 刘维民. 高通量计算二维材料界面摩擦. , 2023, 72(2): 026801. doi: 10.7498/aps.72.20221676
[3]	李君, 刘立胜, 徐爽, 张金咏. 单轴压缩下Ti₃B₄的力学、电学性能及变形机制的第一性原理研究. , 2020, 69(4): 043102. doi: 10.7498/aps.69.20191194
[4]	黄瑞, 李春, 金蔚, GeorgiosLefkidis, WolfgangHübner. 双磁性中心内嵌富勒烯Y₂C₂@C₈₂-C₂(1)中的超快自旋动力学行为. , 2019, 68(2): 023101. doi: 10.7498/aps.68.20181887
[5]	付宝勤, 侯氢, 汪俊, 丘明杰, 崔节超. 钨空位捕获氢及其解离过程的分子动力学. , 2019, 68(24): 240201. doi: 10.7498/aps.68.20190701
[6]	沙莎, 王伟丽, 吴宇昊, 魏炳波. 深过冷条件下Co7Mo6金属间化合物的枝晶生长和维氏硬度研究. , 2018, 67(4): 046402. doi: 10.7498/aps.67.20172156
[7]	王欣欣, 张颖, 周洪波, 王金龙. 铌对钨中氦行为影响的第一性原理研究. , 2014, 63(4): 046103. doi: 10.7498/aps.63.046103
[8]	牛海波, 陈光德, 伍叶龙, 耶红刚. 空位对纤锌矿型AlN自发极化影响的最大局域化Wannier函数方法研究. , 2014, 63(16): 167701. doi: 10.7498/aps.63.167701
[9]	黎军军, 赵学坪, 陶强, 黄晓庆, 朱品文, 崔田, 王欣. 二硼化钛的高温高压制备及其物性. , 2013, 62(2): 026202. doi: 10.7498/aps.62.026202
[10]	徐爽, 郭雅芳. 纳米铜薄膜塑性变形中空位型缺陷形核与演化的分子动力学研究. , 2013, 62(19): 196201. doi: 10.7498/aps.62.196201
[11]	魏哲, 袁健美, 李顺辉, 廖建, 毛宇亮. 含空位二维六角氮化硼电子和磁性质的密度泛函研究. , 2013, 62(20): 203101. doi: 10.7498/aps.62.203101
[12]	李宇波, 王骁, 戴庭舸, 袁广中, 杨杭生. 第一性原理计算研究立方氮化硼空位的电学和光学特性. , 2013, 62(7): 074201. doi: 10.7498/aps.62.074201
[13]	金硕, 孙璐. 带有碳杂质的钨中氢稳定性的第一性原理研究. , 2012, 61(4): 046104. doi: 10.7498/aps.61.046104
[14]	原鹏飞, 祝文军, 徐济安, 刘绍军, 经福谦. BeO高压相变和声子谱的第一性原理计算. , 2010, 59(12): 8755-8761. doi: 10.7498/aps.59.8755
[15]	李金, 桂贵, 孙立忠, 钟建新. 单轴大应变下二维六角氮化硼的结构变化. , 2010, 59(12): 8820-8828. doi: 10.7498/aps.59.8820
[16]	王超营, 王振清, 孟庆元. 空位的第一性原理及经验势函数的对比研究. , 2010, 59(5): 3370-3376. doi: 10.7498/aps.59.3370
[17]	顾娟, 王山鹰, 苟秉聪. Au和3d过渡金属元素混合团簇结构、电子结构和磁性的研究. , 2009, 58(5): 3338-3351. doi: 10.7498/aps.58.3338
[18]	宋庆功, 姜恩永, 裴海林, 康建海, 郭英. 插层化合物LixTiS2中Li离子-空位二维有序结构稳定性的第一性原理研究. , 2007, 56(8): 4817-4822. doi: 10.7498/aps.56.4817
[19]	张超, 王永亮, 颜超, 张庆瑜. 替位杂质对低能Pt原子与Pt(111)表面相互作用影响的分子动力学模拟. , 2006, 55(6): 2882-2891. doi: 10.7498/aps.55.2882
[20]	胡晓君, 戴永兵, 何贤昶, 沈荷生, 李荣斌. 空位在金刚石近(001)表面扩散的分子动力学模拟. , 2002, 51(6): 1388-1392. doi: 10.7498/aps.51.1388

计量

文章访问数: 6228
PDF下载量: 121
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板