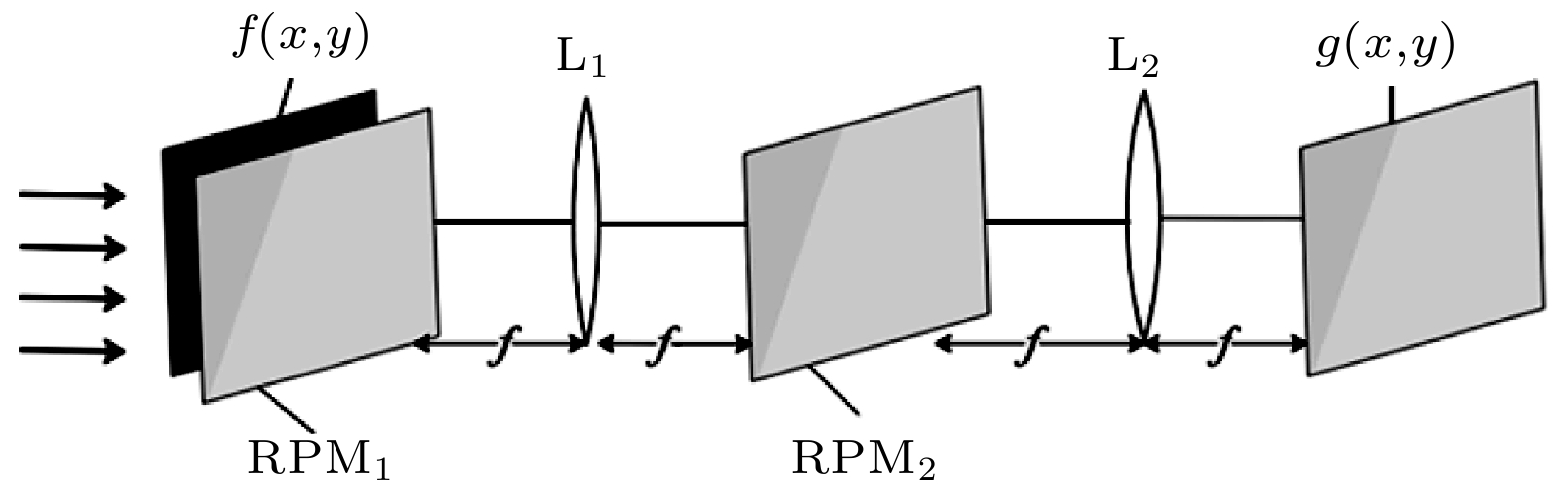
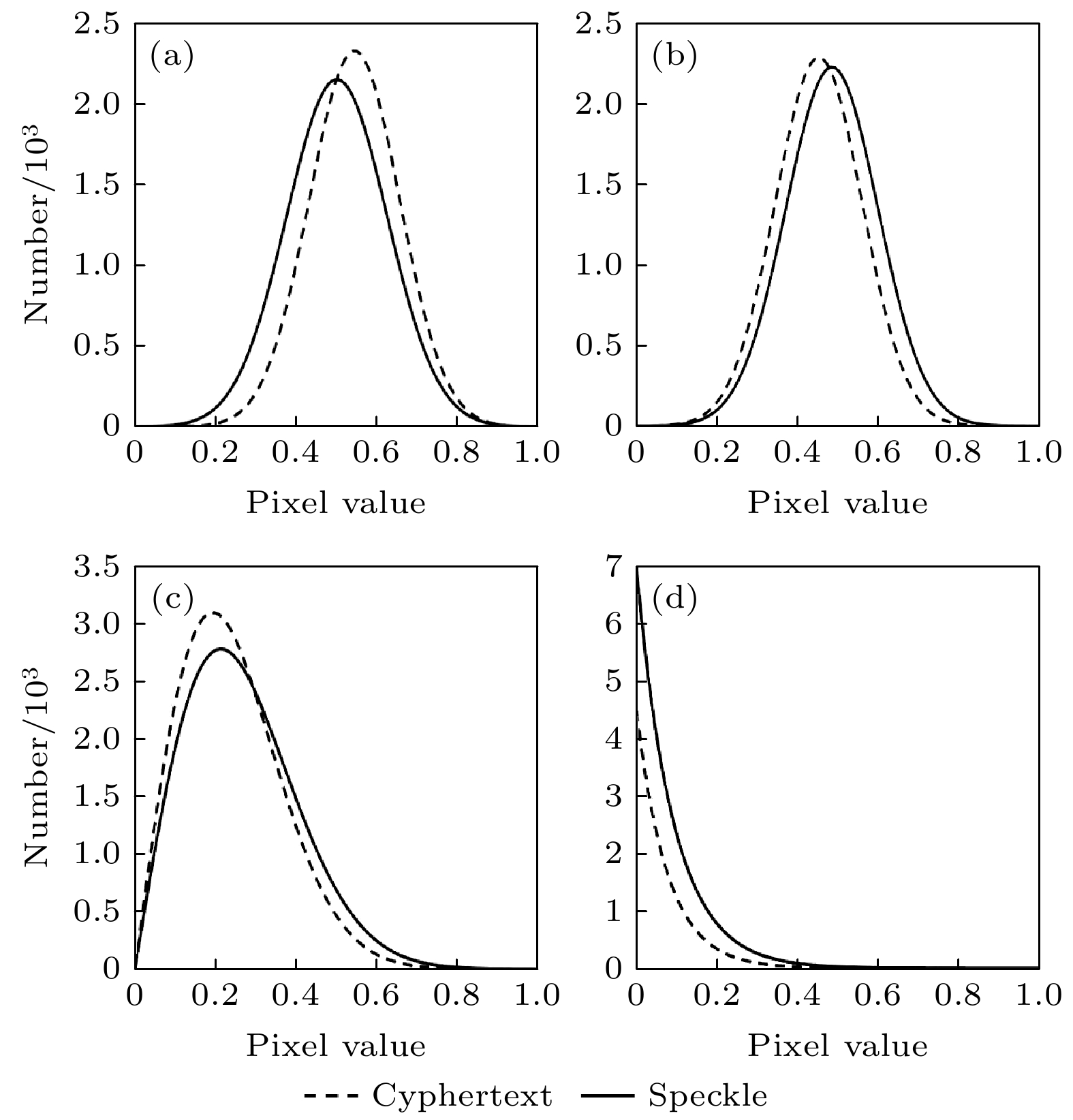
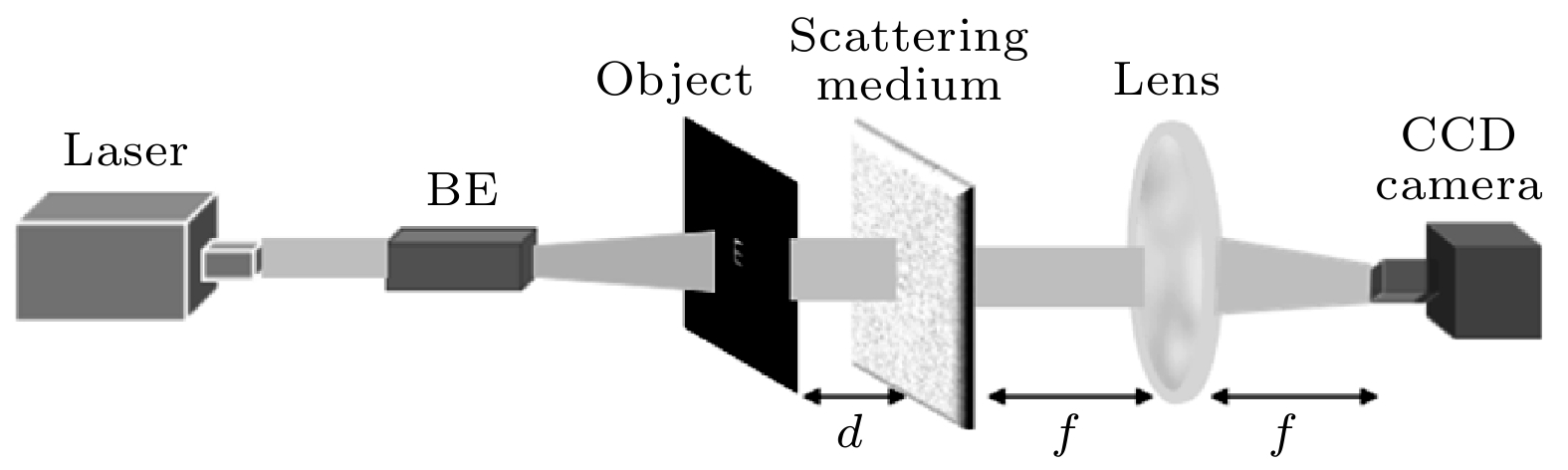
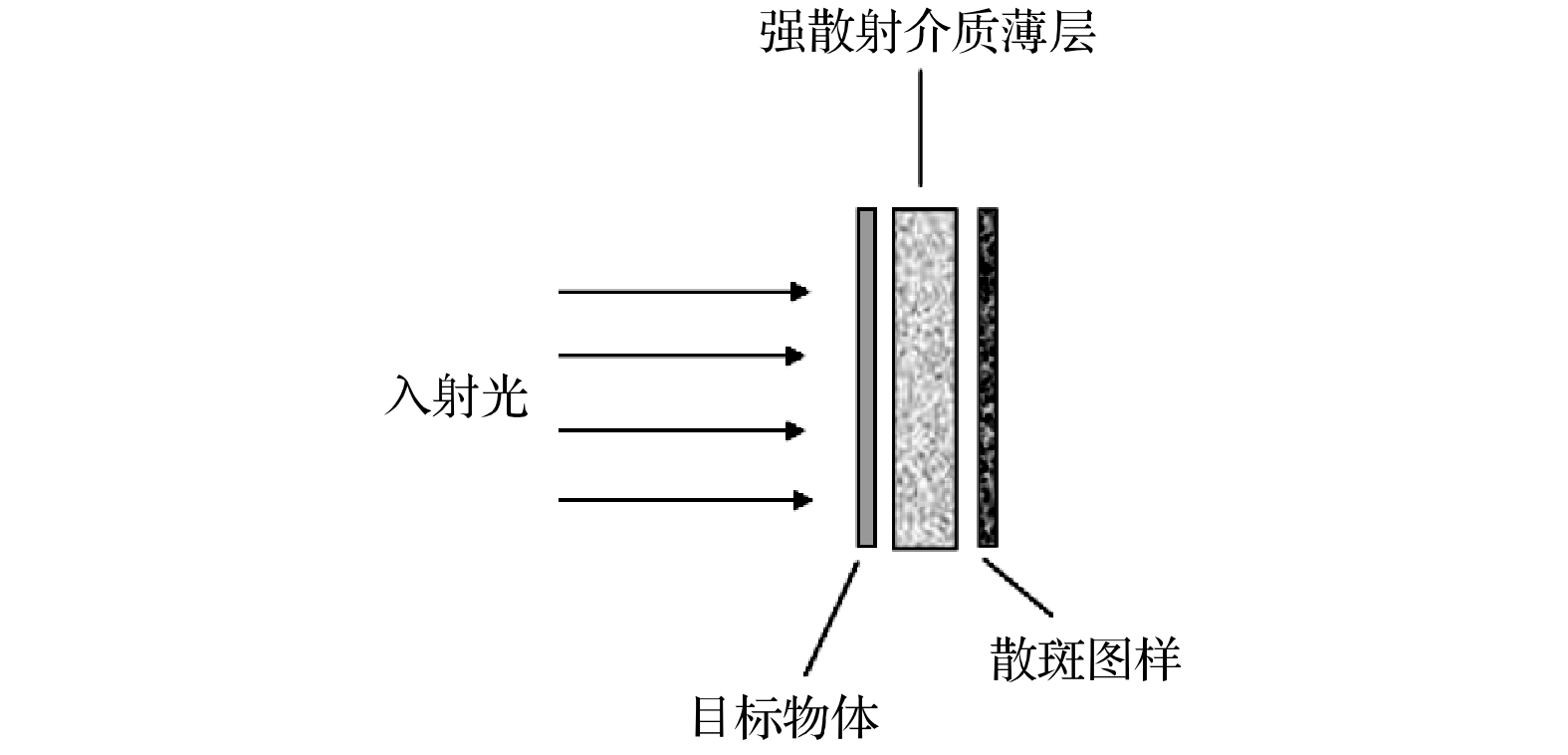
-
薄层强散射介质的散射系统只会引起入射光波的振幅和相位分布变化, 但不会导致总能量的衰减. 这一过程可以看成光波被散射系统编码的过程, 与双随机加密系统极为相似. 本文首先证明了载有目标信息的光波在通过薄层强散射介质的散射系统时所产生散斑的分布特性, 与双随机加密系统加密同一明文目标所得到的密文分布特性具有高度的相似性. 然后, 本文将该散射系统视为一个双随机加密系统, 并利用相位恢复算法精确地计算出该散射系统所对应的两块随机相位密钥, 同时证明了这两块密钥板还可以成功地从该散射系统所得到的其他任何散斑中恢复出对应的原始图像. 最后, 为了进一步证明二者的等价性, 本文使用一种适用于双随机加密系统的唯密文攻击方法, 成功地破解了薄层强散射介质的散射系统, 得到了较好结果.The scattering system through a highly scattering thin layer only affects the amplitude and phase distribution of incident light wave, but does not lead the total energy to be attenuated. This process can be regarded as a process that light wave is encoded by the scattering medium, which is similar to a double random phase encryption system. In this paper, firstly, it is proved that the distribution characteristics of speckle generated by the light wave carrying the target information through a strongly scattering thin layer are highly similar to the distribution characteristics of cyphertext obtained by the double random phase encryption system encrypting the same plaintext target. Therefore, the scattering system is seen as a double random phase encryption system, and the two random phase keys corresponding to the scattering system are calculated accurately by using the phase recovery algorithm. At the same time, it is proved that these two key boards can successfully reconstruct the original images corresponding to any other speckles obtained by the scattering system. Finally, a cyphertext-only attack method to attack a scattering system through a highly scattering thin layer is used to further prove the equivalence of two key boards and the good results are obtained. Since imaging through a scattering medium is an extremely complicated process, we actually simplify the corresponding process ideally. It should be noted that the equivalent system means that the incident-surface-to-exit-surface of scattering medium is equivalent to the incident-surface-to-exit-surface of DRPE system. However, in the actual process, there are still two diffraction processes: one is the diffraction process from the object to the incident surface and the other is the diffraction process from the output surface to the receiving surface. These two diffraction processes will cause the incident image and the output image of scattering medium to have a certain diffraction effect. We believe that under ideal conditions, due to the equivalence between the thin-layer strong scattering system and the DRPE system, theoretically all pure ciphertext attack methods applicable to the DRPE system can be applied to the speckle recovery of the thin-layer strong scattering system. In the future, it is possible to develop more methods of using system equivalence to crack the scattered light field. We hope this article can provide a new idea for scattering imaging.
-
Keywords:
- highly scattering system /
- double random phase encryption system /
- phase recovery algorithm /
- image reconstruction
[1] Mujumdar S, Ramachandran H 2004 Opt. Commun. 241 1
Google Scholar
[2] Wu P F, Liang Z, Zhao X, Su L, Song L P 2017 Appl. Optics. 56 3335
Google Scholar
[3] Nagar H, Dekel E, Kasimov D, Roichman Y 2018 Opt. Lett. 43 190
Google Scholar
[4] Katz O, Small E, Silberberg Y 2012 Nat. Photonics. 6 549
Google Scholar
[5] Wu T F, Dong J, Shao X P, Gigan S 2017 Opt. Express. 25 27182
Google Scholar
[6] Wu T F, Katz O, Shao X P, Gigan S 2016 Opt. Lett. 41 5003
Google Scholar
[7] Shao X P, Wu T F, Gong C M 2013 Opt. Eng. 52 113
[8] Cui M 2011 Opt. Lett. 36 870
Google Scholar
[9] Conkey D B, Caravaca-Aguirre A M, Piestun R 2012 Opt. Express. 20 1733
Google Scholar
[10] Liu J T, Wang J N, Li W, Sun X Y, Zhu L, Guo C F, Shao X P 2018 IEEE Photonics J. 10 1
[11] Chaigne T, Katz O, Boccara A C, Fink M, Bossy E, Gigan S 2013 Nat. Photonics 8 58
[12] 龚昌妹 2017 博士学位论文(西安: 西安电子科技大学)
Gong C M 2017 Ph .D. Dissertation (Xi’an: Xidian University) (in Chinese)
[13] Katz O, Heidmann P, Fink M, Gigan S 2014 Nat. Photonics. 8 784
[14] 宋洪胜, 程传福, 张宁玉, 任晓荣滕树云徐至展 2005 54 669
Google Scholar
Song H S, Cheng C F, Zhang N Y, Ren X R, Ten S Y, Xu Z Z 2005 Acta Phys. Sin. 54 669
Google Scholar
[15] Idell P S, Fienup J R, Goodman R S 1987 Opt. Lett. 12 858
Google Scholar
[16] Li G W, Yang W Q, Li D Y, Situ G H 2017 Opt. Express 25 8690
Google Scholar
[17] Guo C L, Liu S, Sheridan J T 2015 Appl. Optics. 54 4698
Google Scholar
[18] Lowenthal S, Arsenault H 1970 J. Opt. Soc. Am. 60 1478
Google Scholar
[19] Goodman J W 2000 Statistical Optics (New York: Wiley) pp320—390
[20] Refregier P, Javidi B 1995 Opt. Lett. 20 767
Google Scholar
[21] 吴腾飞 2018 博士学位论文 (西安: 西安电子科技大学)
Wu T F 2018 Ph. D. Dissertation (Xi’an: Xidian University) (in Chinese)
[22] 彭翔, 张鹏, 位恒政, 于斌 2006 55 1130
Google Scholar
Peng X, Zhang P, Wei H Z, Yu B 2006 Acta Phys. Sin. 55 1130
Google Scholar
-
图 3 散斑和密文的统计直方图 (a)实部; (b)虚部; (c)振幅; (d)强度
Fig. 3. Statistical distribution histogram of speckle and cyphertext: (a) Real part; (b) imaginary part; (c) amplitude (d) intensity.
图 4 (a)原始图像; (b) 经过强散射薄层后的散斑; (c)第一块密钥板; (d)第二块密钥板;(e)另一原始图像; (f)利用两块密钥板解密出的图像
Fig. 4. (a) Original image;(b) speckle suffered highly thin scatter layer; (c) first encryption key; (d) second encryption key; (e) another original image; (f) decrypted image by two keys.
图 5 (a)第一块随机相位板统计分布直方图;(b)第二块随机相位板统计分布直方图
Fig. 5. (a) The histogram of first random phase key; (b) the histogram of second random phase key.
图 7 (a)目标物体; (b)傅里叶域散斑强度; (c)ESD的估计值; (d)恢复出的目标图像
Fig. 7. (a) Original plaintext image; (b) Fourier-domain speckle intensity;(c) estimated ESD; (d) recovered plaintext image.
-
[1] Mujumdar S, Ramachandran H 2004 Opt. Commun. 241 1
Google Scholar
[2] Wu P F, Liang Z, Zhao X, Su L, Song L P 2017 Appl. Optics. 56 3335
Google Scholar
[3] Nagar H, Dekel E, Kasimov D, Roichman Y 2018 Opt. Lett. 43 190
Google Scholar
[4] Katz O, Small E, Silberberg Y 2012 Nat. Photonics. 6 549
Google Scholar
[5] Wu T F, Dong J, Shao X P, Gigan S 2017 Opt. Express. 25 27182
Google Scholar
[6] Wu T F, Katz O, Shao X P, Gigan S 2016 Opt. Lett. 41 5003
Google Scholar
[7] Shao X P, Wu T F, Gong C M 2013 Opt. Eng. 52 113
[8] Cui M 2011 Opt. Lett. 36 870
Google Scholar
[9] Conkey D B, Caravaca-Aguirre A M, Piestun R 2012 Opt. Express. 20 1733
Google Scholar
[10] Liu J T, Wang J N, Li W, Sun X Y, Zhu L, Guo C F, Shao X P 2018 IEEE Photonics J. 10 1
[11] Chaigne T, Katz O, Boccara A C, Fink M, Bossy E, Gigan S 2013 Nat. Photonics 8 58
[12] 龚昌妹 2017 博士学位论文(西安: 西安电子科技大学)
Gong C M 2017 Ph .D. Dissertation (Xi’an: Xidian University) (in Chinese)
[13] Katz O, Heidmann P, Fink M, Gigan S 2014 Nat. Photonics. 8 784
[14] 宋洪胜, 程传福, 张宁玉, 任晓荣滕树云徐至展 2005 54 669
Google Scholar
Song H S, Cheng C F, Zhang N Y, Ren X R, Ten S Y, Xu Z Z 2005 Acta Phys. Sin. 54 669
Google Scholar
[15] Idell P S, Fienup J R, Goodman R S 1987 Opt. Lett. 12 858
Google Scholar
[16] Li G W, Yang W Q, Li D Y, Situ G H 2017 Opt. Express 25 8690
Google Scholar
[17] Guo C L, Liu S, Sheridan J T 2015 Appl. Optics. 54 4698
Google Scholar
[18] Lowenthal S, Arsenault H 1970 J. Opt. Soc. Am. 60 1478
Google Scholar
[19] Goodman J W 2000 Statistical Optics (New York: Wiley) pp320—390
[20] Refregier P, Javidi B 1995 Opt. Lett. 20 767
Google Scholar
[21] 吴腾飞 2018 博士学位论文 (西安: 西安电子科技大学)
Wu T F 2018 Ph. D. Dissertation (Xi’an: Xidian University) (in Chinese)
[22] 彭翔, 张鹏, 位恒政, 于斌 2006 55 1130
Google Scholar
Peng X, Zhang P, Wei H Z, Yu B 2006 Acta Phys. Sin. 55 1130
Google Scholar
下载:
计量
- 文章访问数: 3713
- PDF下载量: 46
- 被引次数: 0
