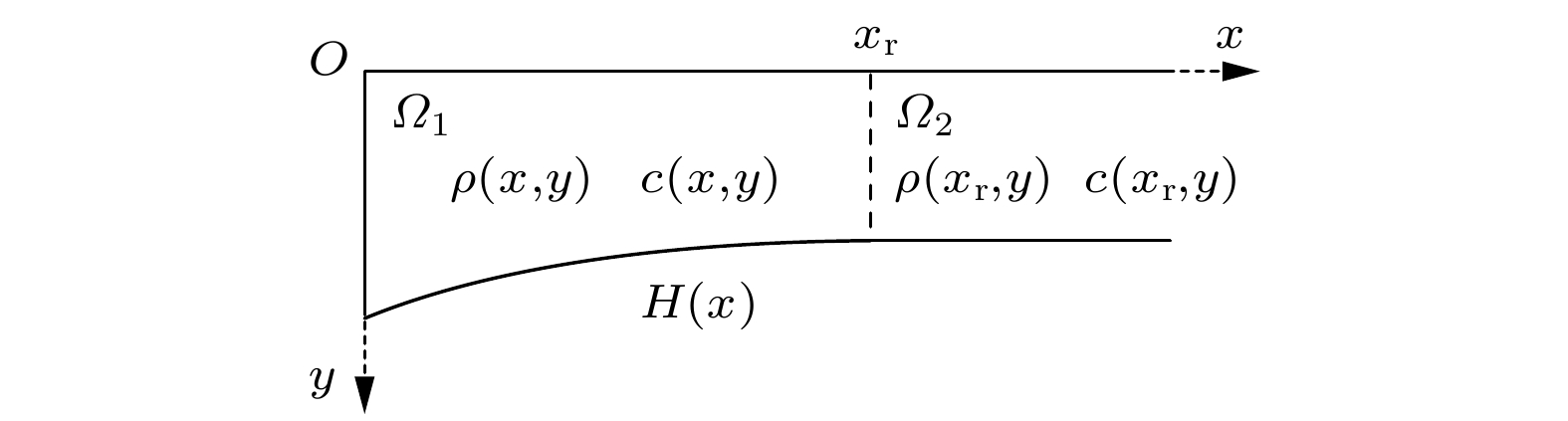
-
针对介质参数及海底边界水平变化波导中的声传播问题, 本文基于多模态导纳法提出一种能量守恒且便于数值稳定求解的耦合模态方法. 将声压表示为一组正交完备的本地本征函数之和, 对声压满足的Helmholtz方程在本地本征函数上作投影, 推导出关于声压模态系数的二阶耦合模态方程组. 耦合矩阵直观描述水平变化因素对模态耦合的贡献. 为避免直接求解二阶耦合模态方程组可能遇到的数值发散问题, 将其重构为两个耦合的一阶演化方程组, 引入导纳矩阵并使用Magnus数值积分方法获得稳定的声场解. 利用该耦合模态方法数值计算水平变化波导中的声场, 并与COMSOL参考解比较, 结果表明该耦合模态理论能够精确求解水平变化波导中的点源及分布源传播问题.The sound propagation problems in range-dependent waveguides are a common topic in underwater acoustics. The range-dependent factors, involving volumetric and bathymetric variations, significantly influence the propagation of sound energy and information. In this paper, a coupled-mode method based on the multimodal admittance method is presented for analyzing the sound propagation and scattering problems in range-dependent waveguides. The sound field is expanded in terms of a local basis with range-dependent modal amplitudes. The local basis corresponds to the transverse modes in a waveguide with constant physical parameters and constant cross section equal to the local cross section in the range-dependent waveguide. This local basis takes the advantage that it is easier to compute than the usual local modes which are the transverse modes in a waveguide with local physical parameters and constant cross-section equal to the local cross-section, especially for waveguides with complex environments. Projection of the Helmholtz equation that governs the sound pressure onto the local basis gives the second-order coupled mode equations for the modal amplitudes of the sound pressure. The correct boundary conditions are used in the derivation, giving rising to boundary matrices, in order to guarantee the conservation of energy among modes. The second-order coupled mode equations include coupled matrices and boundary matrices, which directly describe the effect of mode coupling due to contribution from volumetric variation (range-dependent physical parameters) and bathymetric variation (range-dependent boundaries). By introducing the admittance matrix, the second-order coupled mode equations are reduced to two sets of first-order evolution equations. The Magnus integration method is used to solve the first-order evolution equations. These first-order evolution equations allow us to obtain the numerical stable solutions and avoid the numerical divergence due to the exponential growth of evanescent modes. The numerical examples are presented for the waveguides with range-dependent physical parameters or range-dependent boundaries. The agreement between the results computed with the coupled mode method and COMSOL verifies the accuracy of the coupled mode method. Although the analysis and numerical implementation in this paper are based on two-dimensional waveguides in Cartesian coordinate system, it can be generally extended to study more complex waveguides.
[1] Pierce A D 1965 J. Acoust. Soc. Am. 37 19
Google Scholar
[2] Milder D M 1969 J. Acoust. Soc. Am. 46 1259
Google Scholar
[3] Shen J, Tang T, Wang L L 2011 Spectral Methods: Algorithms, Analysis and Applications (Berlin Heidelberg: Springer-Verlag) pp141−180
[4] Pagneux V, Amir N, Kergomard J 1996 J. Acoust. Soc. Am. 100 2034
Google Scholar
[5] Ciarlet P G 2002 The Finite Element Method for Elliptic Problems (New York: SIAM) pp36−55
[6] Alford R M, Kelly K R, Boore D M 1974 Geophysics 39 834
Google Scholar
[7] 杨春梅, 骆文于, 张仁和, 秦继兴 2013 62 094302
Google Scholar
Yang C M, Luo W Y, Zhang R H, Qin J X 2013 Acta Phys. Sin. 62 094302
Google Scholar
[8] Rutherford S R, Hawker K E 1981 J. Acoust. Soc. Am. 70 554
Google Scholar
[9] Fawcett J A 1992 J. Acoust. Soc. Am. 92 290
Google Scholar
[10] Abawi A T 2002 J. Acoust. Soc. Am. 111 160
Google Scholar
[11] 彭朝晖, 张仁和 2005 声学学报 30 97
Google Scholar
Peng Z H, Zhang R H 2005 Acta Acustica. 30 97
Google Scholar
[12] 莫亚枭, 朴胜春, 张海刚, 李丽 2014 63 214302
Google Scholar
Mo Y X, Piao S C, Zhang H G, Li L 2014 Acta Phys. Sin. 63 214302
Google Scholar
[13] Jensen F B, Kuperman W A, Porter M B, Schmidt H 2011 Computational Ocean Acoustics (New York: Springer) pp403−411
[14] Pagneux V 2010 J. Comput. Appl. Math. 234 1834
Google Scholar
[15] Félix S, Pagneux V 2001 J. Acoust. Soc. Am. 110 1329
Google Scholar
[16] Schiff J, Shnider S 1999 SIAM J. Numer. Anal. 36 1392
Google Scholar
[17] Lu Y Y, McLaughlin J R 1996 J. Acoust. Soc. Am. 100 1432
Google Scholar
[18] Pierce A D 1983 J. Acoust. Soc. Am. 74 1837
Google Scholar
[19] Shmelev A A, Lynch J F, Lin Y T, Schmidt H 2014 J. Acoust. Soc. Am. 135 2496
Google Scholar
[20] Evans R B 1986 J. Acoust. Soc. Am. 80 1414
Google Scholar
[21] Qin J X, Luo W Y, Zhang R H, Yang C M 2013 Chin. Phys. Lett. 30 074301
Google Scholar
[22] Félix S, Pagneux V 2002 Wave Motion 36 157
Google Scholar
[23] Maurel A, Mercier J F 2012 J. Acoust. Soc. Am. 131 1874
Google Scholar
[24] Maurel A, Mercier J F, Pagneux V 2014 Proc. R. Soc. A 470 20130448
Google Scholar
[25] Lu Y Y 2005 J. Comput. Appl. Math. 173 247
Google Scholar
[26] Li Q, Liu J, Guo W 2020 Chin. Phys. B 29 014303
Google Scholar
[27] Preisig J C, Duda T F 1997 IEEE J. Oceanic Eng. 22 256
Google Scholar
[28] Favraud G, Pagneux V 2015 Proc. R. Soc. A 471 20140782
Google Scholar
[29] Westwood E K, Koch R A 1999 J. Acoust. Soc. Am. 106 2513
Google Scholar
-
图 2 水平变化波导中的声场(声源为分布源, 频率为20 Hz) (a) 利用CMM计算得到的声压幅值分布, 截断数
$N = 10$ ; (b) 利用COMSOL计算得到的声压幅值分布; (c) 深度为20 m处, 声压幅值的水平分布; (d) 深度为50 m处, 声压幅值的水平分布Fig. 2. Sound fields in a range-dependent waveguide (the source is a distributed source at 20 Hz): (a) Sound field computed by CMM where the truncation number is
$N = 10$ ; (b) sound field computed with COMSOL; (c) sound field distribution along x direction at depth 20 m; (d) sound field distribution along x direction at depth 50 m.
图 3 水平变化波导中的声场(声源为位于
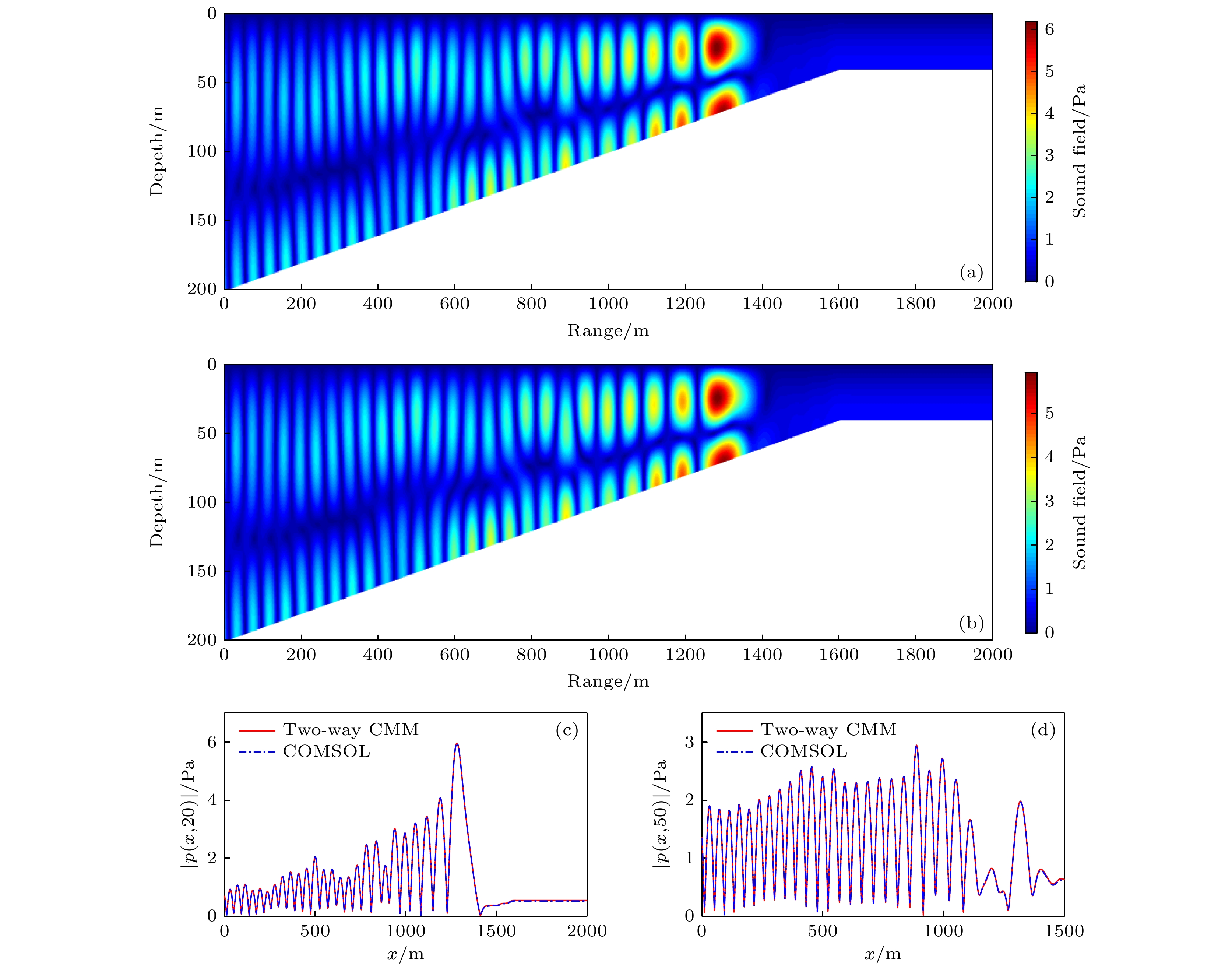
$(0, 10)$ m处的点源, 频率为20 Hz) (a) 利用双向CMM计算得到的声压幅值分布, 截断数$N = 50$ ; (b) 利用COMSOL计算得到的声压幅值分布; (c) 深度为71 m处, 声压幅值的水平分布; (d) 深度为101 m处, 声压幅值的水平分布Fig. 3. Sound fields in a range-dependent waveguide generated by a point source at
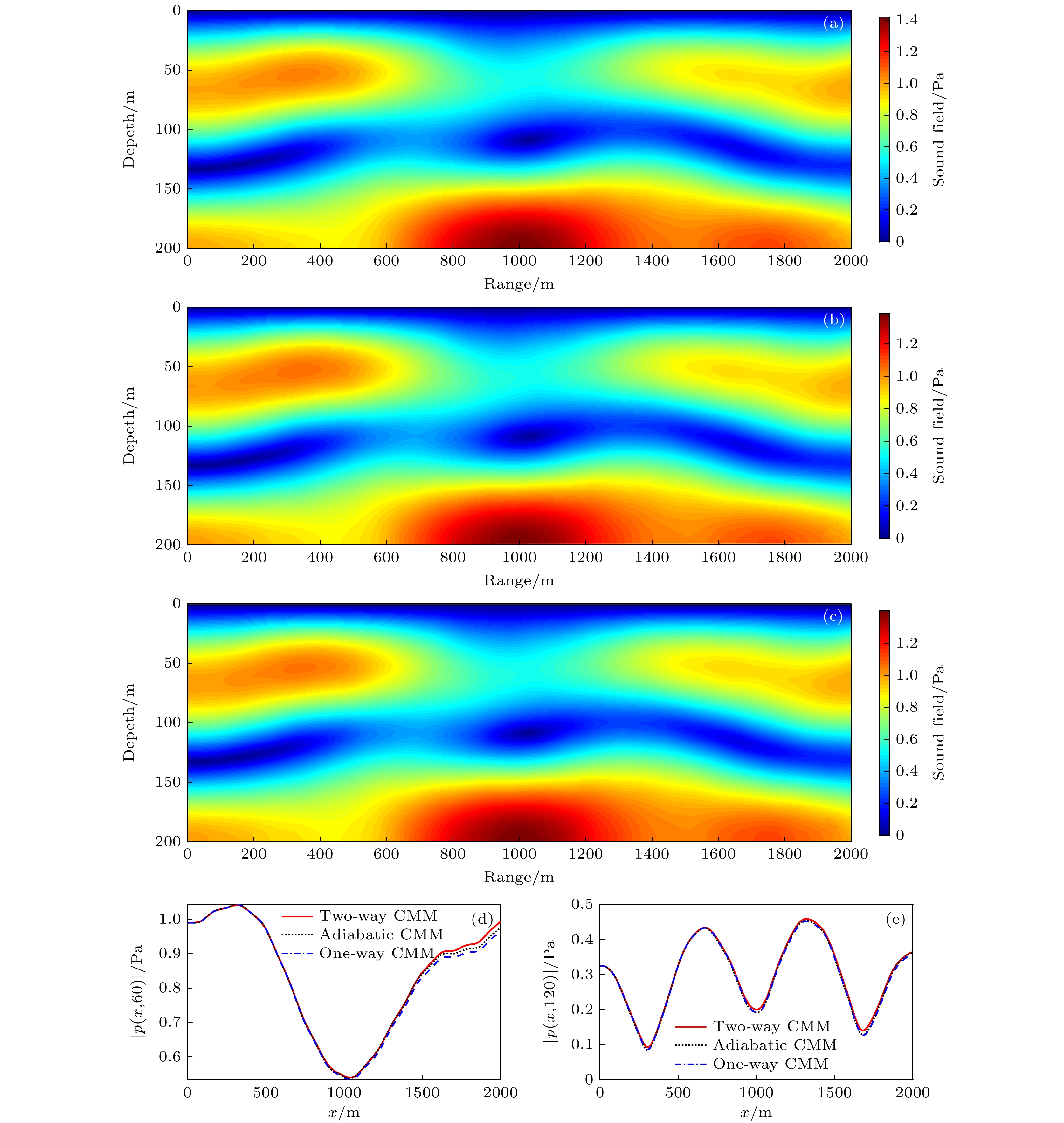
$(0, 10)$ m (the frequency is 20 Hz): (a) Sound field computed by CMM where the truncation number is$N = 50$ ; (b) sound field computed with COMSOL; (c) sound field distribution along x direction at depth 71 m; (d) sound field distribution along x direction at depth 101 m.
图 4 水平缓变波导中的声场(声源为分布源, 频率为20 Hz) (a) 利用双CMM计算得到的声压幅值分布; (b) 利用单向近似CMM计算得到的声压幅值分布; (c) 利用绝热近似CMM计算得到的声压幅值分布; (d) 深度为60 m处, 声压幅值的水平分布; (e) 深度为120 m处, 声压幅值的水平分布
Fig. 4. Sound fields in a waveguide with weak range dependence generated by a distributed source (the frequency is 20 Hz): (a) Sound field computed by two-way CMM; (b) sound field computed with one-way CMM; (c) sound field computed with adiabatic CMM; (d) sound field distribution along x direction at depth 60 m; (e) sound field distribution along x direction at depth 120 m.
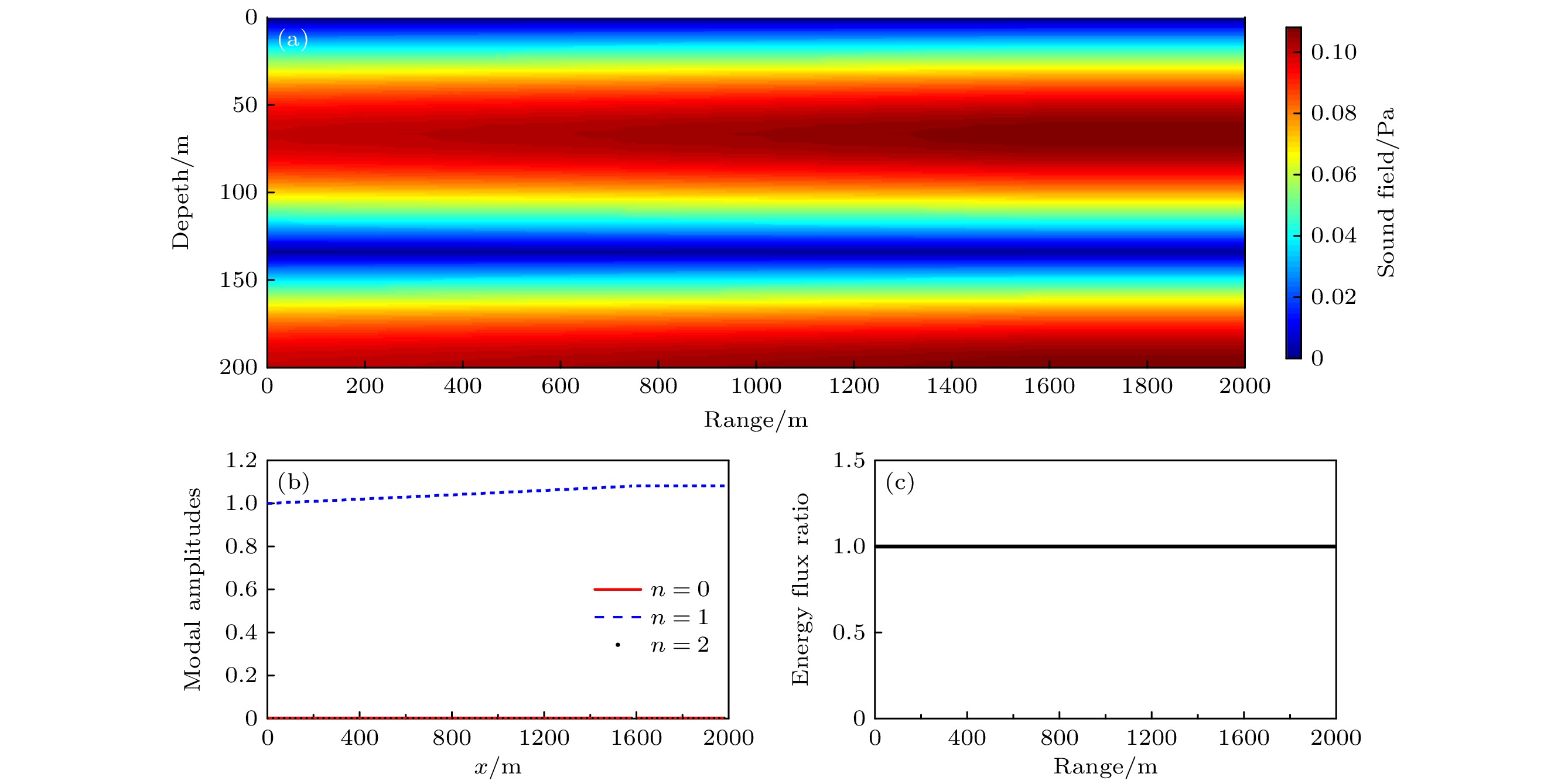
图 5 密度均匀、声速水平变化波导中的声传播(声源为第二阶模态, 频率为10 Hz) (a)声压幅值分布; (b)声压的模态系数的水平分布; (c)归一化能流
Fig. 5. Sound propagation in a waveguide with constant mass density and range-dependent sound speed (the source is the second local mode, and its frequency is 10 Hz): (a) Sound field; (b) modal amplitudes distribution; (c) normalized energy flux distribution.
图 6 密度均匀、声速及边界水平变化波导中的声传播(声源为第二阶简正波, 频率为10 Hz) (a)声压幅值分布; (b)声压的模态系数的水平分布; (c)归一化能流
Fig. 6. Sound propagation in a waveguide with constant mass density and range-dependent sound speed and boundary (the source is the second local mode and its frequency is 10 Hz): (a) Sound field; (b) modal amplitudes distribution; (c) normalized energy flux distribution.
图 9 浅海孤立子内波波导中的声传播(声源为第一阶简正波, 频率为100 Hz) (a)声压幅值分布; (b)前五阶简正波分量
Fig. 9. Sound propagation in a waveguide with an internal solitary wave (the incident wave is the first mode at 100 Hz): (a) Sound field; (b) modal amplitudes distribution.
-
[1] Pierce A D 1965 J. Acoust. Soc. Am. 37 19
Google Scholar
[2] Milder D M 1969 J. Acoust. Soc. Am. 46 1259
Google Scholar
[3] Shen J, Tang T, Wang L L 2011 Spectral Methods: Algorithms, Analysis and Applications (Berlin Heidelberg: Springer-Verlag) pp141−180
[4] Pagneux V, Amir N, Kergomard J 1996 J. Acoust. Soc. Am. 100 2034
Google Scholar
[5] Ciarlet P G 2002 The Finite Element Method for Elliptic Problems (New York: SIAM) pp36−55
[6] Alford R M, Kelly K R, Boore D M 1974 Geophysics 39 834
Google Scholar
[7] 杨春梅, 骆文于, 张仁和, 秦继兴 2013 62 094302
Google Scholar
Yang C M, Luo W Y, Zhang R H, Qin J X 2013 Acta Phys. Sin. 62 094302
Google Scholar
[8] Rutherford S R, Hawker K E 1981 J. Acoust. Soc. Am. 70 554
Google Scholar
[9] Fawcett J A 1992 J. Acoust. Soc. Am. 92 290
Google Scholar
[10] Abawi A T 2002 J. Acoust. Soc. Am. 111 160
Google Scholar
[11] 彭朝晖, 张仁和 2005 声学学报 30 97
Google Scholar
Peng Z H, Zhang R H 2005 Acta Acustica. 30 97
Google Scholar
[12] 莫亚枭, 朴胜春, 张海刚, 李丽 2014 63 214302
Google Scholar
Mo Y X, Piao S C, Zhang H G, Li L 2014 Acta Phys. Sin. 63 214302
Google Scholar
[13] Jensen F B, Kuperman W A, Porter M B, Schmidt H 2011 Computational Ocean Acoustics (New York: Springer) pp403−411
[14] Pagneux V 2010 J. Comput. Appl. Math. 234 1834
Google Scholar
[15] Félix S, Pagneux V 2001 J. Acoust. Soc. Am. 110 1329
Google Scholar
[16] Schiff J, Shnider S 1999 SIAM J. Numer. Anal. 36 1392
Google Scholar
[17] Lu Y Y, McLaughlin J R 1996 J. Acoust. Soc. Am. 100 1432
Google Scholar
[18] Pierce A D 1983 J. Acoust. Soc. Am. 74 1837
Google Scholar
[19] Shmelev A A, Lynch J F, Lin Y T, Schmidt H 2014 J. Acoust. Soc. Am. 135 2496
Google Scholar
[20] Evans R B 1986 J. Acoust. Soc. Am. 80 1414
Google Scholar
[21] Qin J X, Luo W Y, Zhang R H, Yang C M 2013 Chin. Phys. Lett. 30 074301
Google Scholar
[22] Félix S, Pagneux V 2002 Wave Motion 36 157
Google Scholar
[23] Maurel A, Mercier J F 2012 J. Acoust. Soc. Am. 131 1874
Google Scholar
[24] Maurel A, Mercier J F, Pagneux V 2014 Proc. R. Soc. A 470 20130448
Google Scholar
[25] Lu Y Y 2005 J. Comput. Appl. Math. 173 247
Google Scholar
[26] Li Q, Liu J, Guo W 2020 Chin. Phys. B 29 014303
Google Scholar
[27] Preisig J C, Duda T F 1997 IEEE J. Oceanic Eng. 22 256
Google Scholar
[28] Favraud G, Pagneux V 2015 Proc. R. Soc. A 471 20140782
Google Scholar
[29] Westwood E K, Koch R A 1999 J. Acoust. Soc. Am. 106 2513
Google Scholar
下载:
计量
- 文章访问数: 5717
- PDF下载量: 92
- 被引次数: 0
