石墨烯/铝基复合材料在纳米压痕过程中位错与石墨烯相互作用机制的模拟研究

汉芮岐; 宋海洋; 安敏荣; 李卫卫; 马佳丽

doi:10.7498/aps.70.20201591

摘要

石墨烯因其优异的力学性能已成为增强金属基复合材料的理想增强体. 然而, 目前对石墨烯/金属基复合材料在纳米压痕过程中嵌入石墨烯与位错之间的相互作用仍不清晰. 本文采用分子动力学模拟方法, 对90°, 45°和0°位向的石墨烯/铝基复合材料进行了纳米压痕模拟, 研究了压痕加载和卸载过程中石墨烯/铝基复合材料的位错形核及演化, 以获取不同位向的石墨烯与位错的相互作用机制, 并分析其对塑性区的影响. 研究发现, 石墨烯可以有效阻碍位错运动, 并且石墨烯会沿着位错滑移方向发生弹性变形. 在纳米压痕过程中, 位错与不同位向石墨烯之间的相互作用差异导致塑性区的变化趋势不同. 研究结果表明, 在石墨烯/铝基复合材料中, 位向不同的石墨烯对位错阻碍强度和方式不同, 且石墨烯位向为45°的复合材料的硬度高于其他模型. 此外, 石墨烯/铝基复合材料的位错线总长度的演化规律与石墨烯位向紧密相关. 本文研究可为设计和制备高性能石墨烯/金属基复合材料提供一定的理论指导.

关键词:

Abstract

Graphene has been thought to be an ideal reinforcement material for metal matrix composite due to its superior mechanical properties and unique two-dimensional geometry. However, the deformation mechanism of graphene/aluminum matrix composite is still unclear. In this paper, molecular dynamics simulation is used to elucidate the evolution details of the dislocation microstructure and the underlying interaction behavior between dislocation and graphene during nanoindentation of the graphene/aluminum matrix composite with various graphene orientations. To this end, four different cases, i.e. the pure aluminum and the graphene/aluminum matrix composite with the graphene orientation of 90°, 45° and 0° are examined, respectively. Based on the force-indentation depth curve, the interaction behavior between dislocation and graphene and its effect on the plastic zone are analyzed. The results indicate that the graphene can act as an effective dislocation motion barrier, and the elastic deformation of graphene can occur locally along the direction of dislocation slip. Using the visualization technique of dislocation extraction algorithm, the nucleation and propagation of dislocation are investigated. The results show that the differences in interaction behavior between dislocation and graphene with various orientations affect the spreading trend of the plastic zone and the blocking strength of graphene to dislocation. For the composite with the graphene orientations of 45° and 0°, the interaction between graphene and dislocation causes the number of dislocations to increase. Additionally, the plastic zone of the composite with the graphene orientation of 45° is tangent to two symmetrical graphene sheets. For the composite with the graphene orientation of 90°, the interaction between graphene and dislocation shortens the total length of the dislocation line, and the volume shrinkage of plastic zone is most significant after indenter retraction. Here, the hardness is also calculated to quantitatively evaluate the influence of graphene orientation on the mechanical properties of graphene/aluminum matrix composite. The hardness of the composite with the graphene orientation of 45° is highest, which is due to the decrease of the volume of the plastic zone and the increase of dislocation number. The decrease of the hardness of the composite with the graphene orientation of 90° is attributed to the reduction of dislocation number in the plastic zone. However, for the composite with the graphene orientation of 0°, the interaction between graphene and dislocation results in the softening effect, because of a wide range of elastic deformation in the graphene plane. The study can provide a certain theoretical guidance for designing and preparing the high-performance graphene/metal matrix composites.

Keywords:

作者及机构信息

西安石油大学材料科学与工程学院, 西安　710065

通信作者: 宋海洋, hysong@xsyu.edu.cn ; 安敏荣, amr_lr@126.com ;

基金项目: 国家自然科学基金(批准号: 11572259)、陕西省自然科学基金(批准号: 2018JM1013)、西安石油大学材料科学与工程省级优势学科项目(批准号: YS37020203)和西安石油大学研究生创新与实践能力培养项目(批准号: YCS18211006)资助的课题

Authors and contacts

College of Materials Science and Engineering, Xi’an Shiyou University, Xi’an 710065, China

Corresponding author: Song Hai-Yang, hysong@xsyu.edu.cn ; An Min-Rong, amr_lr@126.com ;

Funds: Project supported by the National Natural Science Foundation of China (Grant No. 11572259), the Natural Science Foundation of Shaanxi Province, China (Grant No. 2018JM1013), the Provincial Superiority Discipline of Materials Science and Engineering of Xi’an Shiyou University, China (Grant No. YS37020203), and the Program for Graduate Innovation Fund of Xi’an Shiyou University, China (Grant No. YCS18211006)

文章全文 : translate this paragraph

参考文献

[1]	Miracle D B 2005 Compos. Sci. Technol. 65 2526 Google Scholar
[2]	Tjong S C 2013 Mater. Sci. Eng., R 74 281 Google Scholar
[3]	Novoselov K S, Geim A K, Morozov S V, Jiang D, Zhang Y, Dubonos S V, Grigorieva I V, Firsov A A 2004 Science 306 666 Google Scholar
[4]	范冰冰, 郭焕焕, 李稳, 贾瑜, 张锐 2013 62 148101 Google Scholar Fan B B, Guo H H, Li W, Jia Y, Zhang R 2013 Acta Phys. Sin. 62 148101 Google Scholar
[5]	Zhong T, Li J, Zhang K 2019 J. Appl. Phys. 125 175110 Google Scholar
[6]	Kim Y, Lee J, Yeom M S, Shin J W, Kim H, Cui Y, Kysar J W, Hone J, Jung Y, Jeon S, Han S M 2013 Nat. Commun. 4 2114 Google Scholar
[7]	Bartolucci S F, Paras J, Rafiee M A, Rafiee J, Lee S, Kapoor D, Koratkar N 2011 Mater. Sci. Eng., A 528 7933 Google Scholar
[8]	Ovid’ko I A, Sheinerman A G 2014 J. Phys. D: Appl. Phys. 47 495302 Google Scholar
[9]	Li Z, Guo Q, Li Z, Fan G, Xiong D B, Su Y, Zhang J, Zhang D 2015 Nano Lett. 15 8077 Google Scholar
[10]	Zhao L, Guo Q, Li Z, Xiong D B, Osovski S, Su Y, Zhang D 2019 Int. J. Plast. 116 265 Google Scholar
[11]	马通, 谢红献 2020 69 130202 Google Scholar Ma T, Xian H X 2020 Acta Phys. Sin. 69 130202 Google Scholar
[12]	Lyu G J, Qiao J C, Yao Y, Pelletier J M, Rodney D, Morthomas J, Fusco C 2020 Scr. Mater. 174 39 Google Scholar
[13]	Zhou X, Bu W, Song S, Sansoz F, Huang X 2019 Mater. Des. 182 108093 Google Scholar
[14]	Du Y, Zhou Q, Jia Q, Shi Y, Wang H, Wang J 2020 Mater. Res. Lett. 8 357 Google Scholar
[15]	Charleston J, Agrawal A, Mirzaeifar R 2020 Comput. Mater. Sci. 178 109621 Google Scholar
[16]	Weng S, Ning H, Fu T, Hu N, Zhao Y, Huang C, Peng X 2018 Sci. Rep. 8 3089 Google Scholar
[17]	Shuang F, Aifantis K E 2020 Scr. Mater. 181 70 Google Scholar
[18]	Plimpton S 1995 J. Comput. Phys. 117 1 Google Scholar
[19]	Zha X H, Zhang R Q, Lin Z 2014 J. Chem. Phys. 141 064705 Google Scholar
[20]	Lee Y, Park J Y, Kim S Y, Jun S, Im S 2005 Mech. Mater. 37 1035 Google Scholar
[21]	Mishin Y, Farkas D, Mehl M J, Papaconstantopoulos D A 1999 Phys. Rev. B 59 3393 Google Scholar
[22]	Stuart S J, Tutein A B, Harrison J A 2000 J. Chem. Phys. 112 6472 Google Scholar
[23]	Silvestre N, Faria B, Canongia Lopes J N 2014 Compos. Sci. Technol. 90 16 Google Scholar
[24]	Zhou X, Liu X, Lei J, Yang Q 2020 Comput. Mater. Sci. 172 109342 Google Scholar
[25]	Stukowski A 2010 Model. Simul. Mater. Sci. Eng. 18 015012 Google Scholar
[26]	Faken D, Jónsson H 1994 Comput. Mater. Sci. 2 279 Google Scholar
[27]	Stukowski A, Bulatov V V, Arsenlis A 2012 Model. Simul. Mater. Sci. Eng. 20 085007 Google Scholar
[28]	Remington T P, Ruestes C J, Bringa E M, Remington B A, Lu C H, Kad B, Meyers M A 2014 Acta Mater. 78 378 Google Scholar
[29]	Jiao S, Tu W, Zhang P, Zhang W, Qin L, Sun Z, Chen J 2018 Comput. Mater. Sci. 143 384 Google Scholar
[30]	Chang S W, Nair A K, Buehler M J 2013 Philos. Mag. Lett. 93 196 Google Scholar
[31]	Mortazavi B, Rémond Y, Ahzi S, Toniazzo V 2012 Comput. Mater. Sci. 53 298 Google Scholar
[32]	Gao Y, Ruestes C J, Tramontina D R, Urbassek H M 2015 J. Mech. Phys. Solids 75 58 Google Scholar
[33]	李锐, 刘腾, 陈翔, 陈思聪, 符义红, 刘琳 2018 67 190202 Google Scholar Li R, Liu T, Chen X, Chen S C, Fu Y H, Liu L 2018 Acta Phys. Sin. 67 190202 Google Scholar
[34]	Taylor G I 1934 Proc. R. Soc. London, Ser. A 145 388 Google Scholar
[35]	Bagheripoor M, Klassen R 2020 Mech. Mater. 143 103311 Google Scholar
[36]	Vardanyan V H, Urbassek H M 2019 Comput. Mater. Sci. 170 109158 Google Scholar

施引文献

图 1 (a)纯铝的初始模型; 石墨烯的嵌入方位分别为(b) 90°, (c) 45°和(d) 0°的Gr/Al复合材料的初始模型, 其中蓝色原子为对称的石墨烯片, 绿色原子为铝基体

Fig. 1. (a) Initial model of the pure Al; initial model of the Gr/Al composites with graphene orientations of (b) 90°, (c) 45°, and (d) 0°, where blue atoms represent symmetrical graphene sheets and green atoms are Al matrix.

下载: 全尺寸图片幻灯片

图 2 加载过程中, 纯铝和Gr/Al复合材料的压痕力与压痕深度的关系

Fig. 2. Relationship between indentation force and indentation depth of the pure Al and the Gr/Al composites during the loading stage.

下载: 全尺寸图片幻灯片

图 3 加载过程中, 纯铝和Gr/Al复合材料在特征点b—f的位错线分布图

Fig. 3. Dislocation line distribution diagram of the pure Al and the Gr/Al composites at the characteristic points b–f during the loading stage.

下载: 全尺寸图片幻灯片

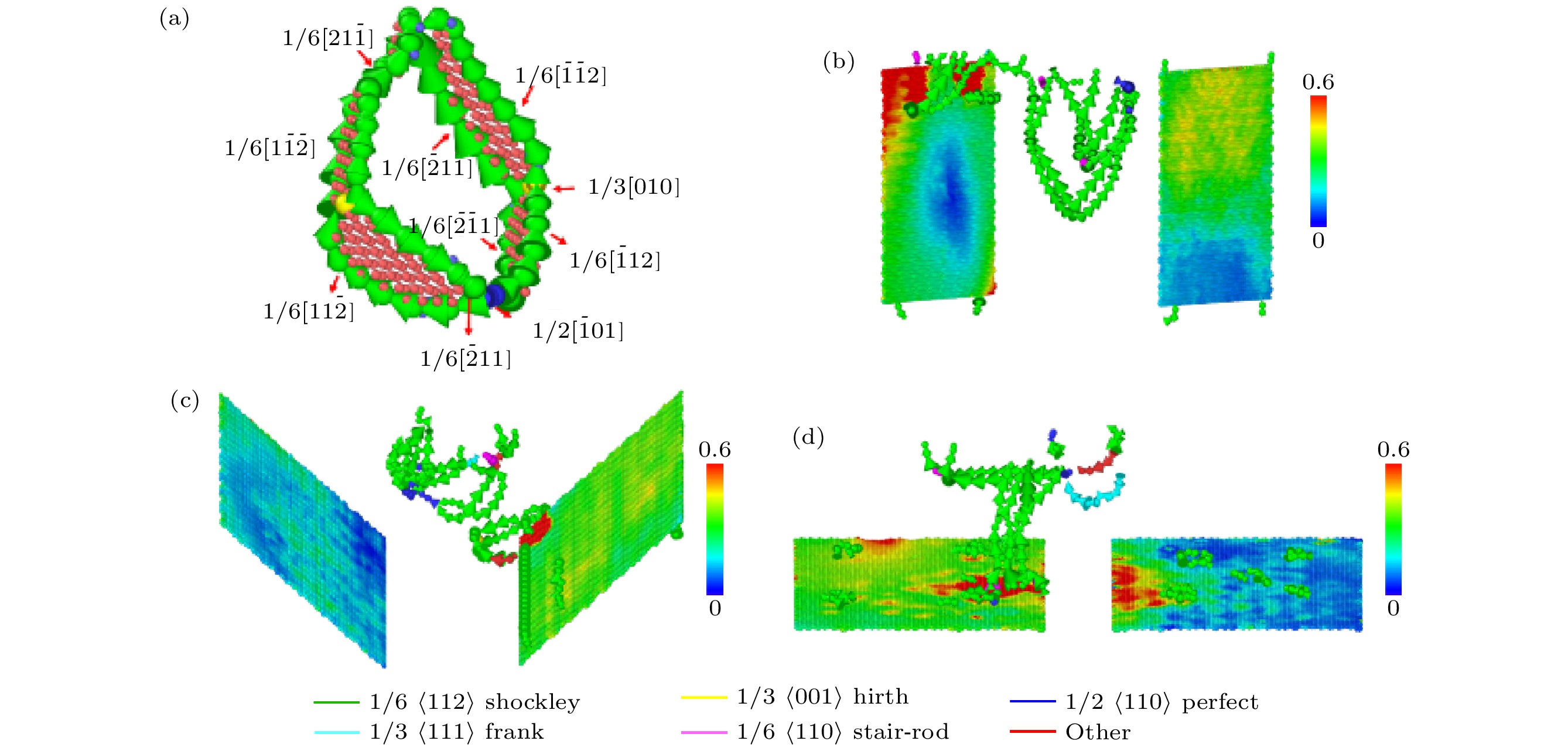
图 4 (a)棱柱形位错环的原子结构图; (b)—(d) Gr/Al复合材料在石墨烯嵌入位向分别为(b) 90°, (c) 45°和(d) 0°, 压痕深度分别为(b) 1.75 nm, (c) 1.59 nm和(d) 1.59 nm时的位错线分布和石墨烯的表面起伏情况

Fig. 4. (a) Atomic snapshot of prismatic dislocation loop; (b)–(d) dislocation line distribution of Gr/Al composites and in-plane height profile of graphene at the indentation depth of (b) 1.75 nm, (c) 1.59 nm, and (d) 1.59 nm, with graphene orientations of (b) 90°, (c) 45°, and (d) 0°.

下载: 全尺寸图片幻灯片

图 5 (a)卸载过程中, 纯铝和Gr/Al复合材料的压痕力与压痕深度的关系; (b) 卸载过程中, 纯铝和Gr/Al复合材料的总位错线长度的演化

Fig. 5. (a) Relationship between indentation force and indentation depth of the pure Al and the Gr/Al composites during the unloading stage; (b) evolution of total dislocation length of the pure Al and the Gr/Al composites during the unloading stage.

下载: 全尺寸图片幻灯片

图 6 卸载过程中, 纯铝和Gr/Al复合材料在不同压痕深度的位错线分布图

Fig. 6. Dislocation line distribution diagram of the pure Al and the Gr/Al composites at various depths during the unloading stage.

下载: 全尺寸图片幻灯片

图 7 纯铝和Gr/Al复合材料在压痕深度3.50和0.00 nm时的微结构, 蓝色虚线表示塑性区

Fig. 7. Microstructures of the pure Al and the Gr/Al composites at indentation depth 3.50 and 0.00 nm, where the blue dotted line indicates the plastic zone.

下载: 全尺寸图片幻灯片

图 8 Gr/Al复合材料的硬度随石墨烯嵌入方位的变化

Fig. 8. Relationship between the hardness of Gr/Al composites and different orientations of graphene.

下载: 全尺寸图片幻灯片

map

[1]	Miracle D B 2005 Compos. Sci. Technol. 65 2526 Google Scholar
[2]	Tjong S C 2013 Mater. Sci. Eng., R 74 281 Google Scholar
[3]	Novoselov K S, Geim A K, Morozov S V, Jiang D, Zhang Y, Dubonos S V, Grigorieva I V, Firsov A A 2004 Science 306 666 Google Scholar
[4]	范冰冰, 郭焕焕, 李稳, 贾瑜, 张锐 2013 62 148101 Google Scholar Fan B B, Guo H H, Li W, Jia Y, Zhang R 2013 Acta Phys. Sin. 62 148101 Google Scholar
[5]	Zhong T, Li J, Zhang K 2019 J. Appl. Phys. 125 175110 Google Scholar
[6]	Kim Y, Lee J, Yeom M S, Shin J W, Kim H, Cui Y, Kysar J W, Hone J, Jung Y, Jeon S, Han S M 2013 Nat. Commun. 4 2114 Google Scholar
[7]	Bartolucci S F, Paras J, Rafiee M A, Rafiee J, Lee S, Kapoor D, Koratkar N 2011 Mater. Sci. Eng., A 528 7933 Google Scholar
[8]	Ovid’ko I A, Sheinerman A G 2014 J. Phys. D: Appl. Phys. 47 495302 Google Scholar
[9]	Li Z, Guo Q, Li Z, Fan G, Xiong D B, Su Y, Zhang J, Zhang D 2015 Nano Lett. 15 8077 Google Scholar
[10]	Zhao L, Guo Q, Li Z, Xiong D B, Osovski S, Su Y, Zhang D 2019 Int. J. Plast. 116 265 Google Scholar
[11]	马通, 谢红献 2020 69 130202 Google Scholar Ma T, Xian H X 2020 Acta Phys. Sin. 69 130202 Google Scholar
[12]	Lyu G J, Qiao J C, Yao Y, Pelletier J M, Rodney D, Morthomas J, Fusco C 2020 Scr. Mater. 174 39 Google Scholar
[13]	Zhou X, Bu W, Song S, Sansoz F, Huang X 2019 Mater. Des. 182 108093 Google Scholar
[14]	Du Y, Zhou Q, Jia Q, Shi Y, Wang H, Wang J 2020 Mater. Res. Lett. 8 357 Google Scholar
[15]	Charleston J, Agrawal A, Mirzaeifar R 2020 Comput. Mater. Sci. 178 109621 Google Scholar
[16]	Weng S, Ning H, Fu T, Hu N, Zhao Y, Huang C, Peng X 2018 Sci. Rep. 8 3089 Google Scholar
[17]	Shuang F, Aifantis K E 2020 Scr. Mater. 181 70 Google Scholar
[18]	Plimpton S 1995 J. Comput. Phys. 117 1 Google Scholar
[19]	Zha X H, Zhang R Q, Lin Z 2014 J. Chem. Phys. 141 064705 Google Scholar
[20]	Lee Y, Park J Y, Kim S Y, Jun S, Im S 2005 Mech. Mater. 37 1035 Google Scholar
[21]	Mishin Y, Farkas D, Mehl M J, Papaconstantopoulos D A 1999 Phys. Rev. B 59 3393 Google Scholar
[22]	Stuart S J, Tutein A B, Harrison J A 2000 J. Chem. Phys. 112 6472 Google Scholar
[23]	Silvestre N, Faria B, Canongia Lopes J N 2014 Compos. Sci. Technol. 90 16 Google Scholar
[24]	Zhou X, Liu X, Lei J, Yang Q 2020 Comput. Mater. Sci. 172 109342 Google Scholar
[25]	Stukowski A 2010 Model. Simul. Mater. Sci. Eng. 18 015012 Google Scholar
[26]	Faken D, Jónsson H 1994 Comput. Mater. Sci. 2 279 Google Scholar
[27]	Stukowski A, Bulatov V V, Arsenlis A 2012 Model. Simul. Mater. Sci. Eng. 20 085007 Google Scholar
[28]	Remington T P, Ruestes C J, Bringa E M, Remington B A, Lu C H, Kad B, Meyers M A 2014 Acta Mater. 78 378 Google Scholar
[29]	Jiao S, Tu W, Zhang P, Zhang W, Qin L, Sun Z, Chen J 2018 Comput. Mater. Sci. 143 384 Google Scholar
[30]	Chang S W, Nair A K, Buehler M J 2013 Philos. Mag. Lett. 93 196 Google Scholar
[31]	Mortazavi B, Rémond Y, Ahzi S, Toniazzo V 2012 Comput. Mater. Sci. 53 298 Google Scholar
[32]	Gao Y, Ruestes C J, Tramontina D R, Urbassek H M 2015 J. Mech. Phys. Solids 75 58 Google Scholar
[33]	李锐, 刘腾, 陈翔, 陈思聪, 符义红, 刘琳 2018 67 190202 Google Scholar Li R, Liu T, Chen X, Chen S C, Fu Y H, Liu L 2018 Acta Phys. Sin. 67 190202 Google Scholar
[34]	Taylor G I 1934 Proc. R. Soc. London, Ser. A 145 388 Google Scholar
[35]	Bagheripoor M, Klassen R 2020 Mech. Mater. 143 103311 Google Scholar
[36]	Vardanyan V H, Urbassek H M 2019 Comput. Mater. Sci. 170 109158 Google Scholar

[1]	刘青阳, 徐青松, 李瑞. 氮掺杂对石墨烯摩擦学特性影响的分子动力学模拟. , 2022, 71(14): 146801. doi: 10.7498/aps.71.20212309
[2]	明知非, 宋海洋, 安敏荣. 基于分子动力学模拟的石墨烯镁基复合材料力学行为. , 2022, 71(8): 086201. doi: 10.7498/aps.71.20211753
[3]	陈晶晶, 邱小林, 李柯, 周丹, 袁军军. 纳米晶CoNiCrFeMn高熵合金力学性能的原子尺度分析. , 2022, 71(19): 199601. doi: 10.7498/aps.71.20220733
[4]	李兴欣, 李四平. 退火温度调控多层折叠石墨烯力学性能的分子动力学模拟. , 2020, 69(19): 196102. doi: 10.7498/aps.69.20200836
[5]	李锐, 刘腾, 陈翔, 陈思聪, 符义红, 刘琳. 界面结构对Cu/Ni多层膜纳米压痕特性影响的分子动力学模拟. , 2018, 67(19): 190202. doi: 10.7498/aps.67.20180958
[6]	杨文龙, 韩浚生, 王宇, 林家齐, 何国强, 孙洪国. 聚酰亚胺/功能化石墨烯复合材料力学性能及玻璃化转变温度的分子动力学模拟. , 2017, 66(22): 227101. doi: 10.7498/aps.66.227101
[7]	李艳茹, 何秋香, 王芳, 向浪, 钟建新, 孟利军. 金属纳米薄膜在石墨基底表面的动力学演化. , 2016, 65(3): 036804. doi: 10.7498/aps.65.036804
[8]	王晓媛, 赵丰鹏, 王杰, 闫亚宾. 金属有机框架材料力学、电学及其应变调控特性的第一原理研究. , 2016, 65(17): 178105. doi: 10.7498/aps.65.178105
[9]	林家齐, 李晓康, 杨文龙, 孙洪国, 谢志滨, 修翰江, 雷清泉. 聚酰亚胺/钽铌酸钾纳米颗粒复合材料结构与机械性能分子动力学模拟. , 2015, 64(12): 126202. doi: 10.7498/aps.64.126202
[10]	郑伯昱, 董慧龙, 陈非凡. 基于量子修正的石墨烯纳米带热导率分子动力学表征方法. , 2014, 63(7): 076501. doi: 10.7498/aps.63.076501
[11]	胡兴健, 郑百林, 胡腾越, 杨彪, 贺鹏飞, 岳珠峰. 考虑相界效应的Ni基单晶合金纳米压痕模拟. , 2014, 63(17): 176201. doi: 10.7498/aps.63.176201
[12]	李琳, 王暄, 孙伟峰, 雷清泉. 聚乙烯/银纳米颗粒复合物的分子动力学模拟研究. , 2013, 62(10): 106201. doi: 10.7498/aps.62.106201
[13]	孙伟峰, 王暄. 聚酰亚胺/铜纳米颗粒复合物的分子动力学模拟研究. , 2013, 62(18): 186202. doi: 10.7498/aps.62.186202
[14]	宋海洋, 李玉龙. 堆垛层错和温度对纳米多晶镁变形机理的影响. , 2012, 61(22): 226201. doi: 10.7498/aps.61.226201
[15]	王卫东, 郝跃, 纪翔, 易成龙, 牛翔宇. 不同温度条件下单层石墨烯纳米带弛豫性能的分子动力学研究. , 2012, 61(20): 200207. doi: 10.7498/aps.61.200207
[16]	李青坤, 孙毅, 周玉, 曾凡林. 第一性原理研究hcp-C3碳体环材料的力学性质. , 2012, 61(4): 043103. doi: 10.7498/aps.61.043103
[17]	权伟龙, 李红轩, 吉利, 赵飞, 杜雯, 周惠娣, 陈建敏. 类金刚石薄膜力学特性的分子动力学模拟. , 2010, 59(8): 5687-5691. doi: 10.7498/aps.59.5687
[18]	王华滔, 秦昭栋, 倪玉山, 张文. 不同晶体取向下纳米压痕的多尺度模拟. , 2009, 58(2): 1057-1063. doi: 10.7498/aps.58.1057
[19]	谢芳, 朱亚波, 张兆慧, 张林. 碳纳米管振荡的分子动力学模拟. , 2008, 57(9): 5833-5837. doi: 10.7498/aps.57.5833
[20]	李瑞, 胡元中, 王慧, 张宇军. 单壁碳纳米管在石墨基底上运动的分子动力学模拟. , 2006, 55(10): 5455-5459. doi: 10.7498/aps.55.5455

计量

文章访问数: 6519
PDF下载量: 168
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

石墨烯/铝基复合材料在纳米压痕过程中位错与石墨烯相互作用机制的模拟研究