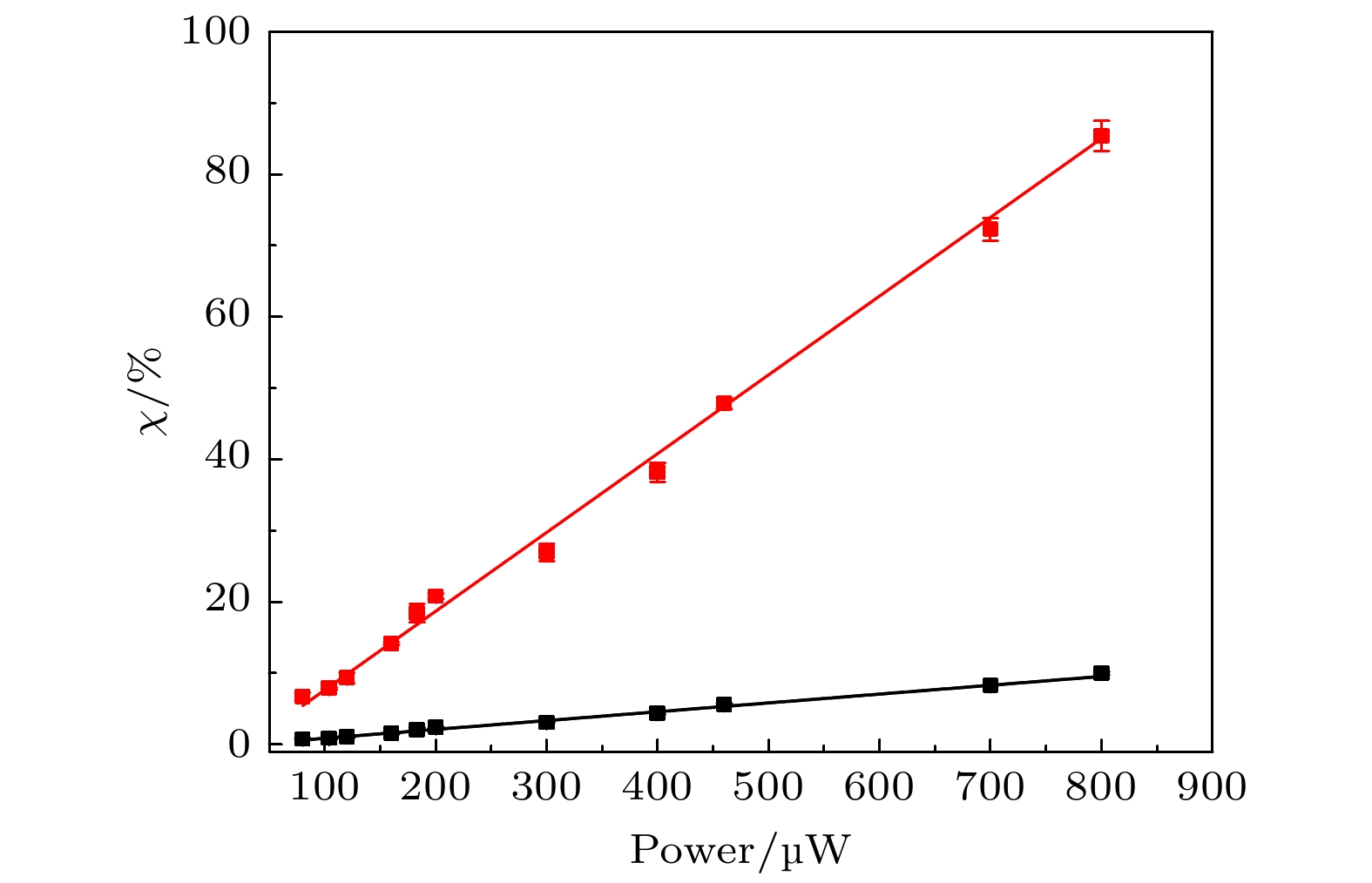
-
原子系综中的Duan-Lukin-Cirac-Zoller (DLCZ)过程是产生光与原子(量子界面)量子关联和纠缠的重要手段. 当一束写光与原子发生作用时, 将会产生斯托克斯(Stokes)光子的自发拉曼散射, 并同时产生一个自旋波(spin-wave)存储在原子系综中, 上述过程即为DLCZ量子记忆产生过程. 这一过程被广泛地研究. 本文将87Rb原子系综放入驻波腔, 并使Stokes光子与光学腔共振, 我们观察到有腔且锁定的情况下Stokes光子产生概率比无腔时增大了8.7倍. 在此条件下研究了Stokes光子产生概率和写光功率的关系, Stokes光子产生概率随写光功率线性增大.
-
关键词:
- Duan-Lukin-Cirac-Zoller方案 /
- 自发拉曼散射 /
- Stokes光子 /
- 驻波腔
The Duan-Lukin-Cirac-Zoller (DLCZ) process in the atomic ensemble is an important means to generate quantum correlation and entanglement between photons and atoms (quantum interface). When a write pulse acts on atoms, the DLCZ quantum memory process will be generated, which has been extensively studied. In the process a spontaneous Raman scattering (SRS) of a Stokes photon is generated, and a spin-wave excitation stored in the atomic ensemble is created at the same time. The higher probability of the generation of Stokes photons will cause more noise and reduce entanglement. On the contrary, the low generation probability of Stokes photons affects the success probability of entanglement distribution on a quantum repeater. How to increase generation probability of Stokes photons without causing more noise is an urgent problem to be resolved. In this work, a 87Rb atomic ensemble is placed in a standing wave cavity which resonates with the Stokes photon. This cavity has a trip length of 0.6 m and a free spectral range (FSR) of 256 MHz. The optical loss of all the optical elements in this cavity is 9%, of which 4% loss originates from the other optical elements and 5% loss from the vacuum chamber of the magneto-optical trap (MOT). The fineness of the cavity with the cold atoms is measured to be ~19.1. By calculating the total probability of Stokes photon emission out of the cavity, we derive the enhancement factor of this standing wave cavity when the cavity loss is l. When this cavity is locked with PDH frequency locking technique, we observe that the production probability of the Stokes photons is 8.7 times higher than that without cavity due to the optical cavity enhancement effect. Under this condition, the relationship between the generation probability of Stokes photons and the power of write beam is studied. The write excitation probability changes linearly with the power of write beam. This work provides an experimental solution to reducing the noise caused by time multimode operation in DLCZ scheme.-
Keywords:
- Duan-Lukin-Cirac-Zoller protocol /
- spontaneous Raman scattering (SRS) /
- Stokes photon /
- standing wave cavity
[1] Sangouard N, Simon C, de Riedmatten H, Gisin N 2011 Rev. Mod. Phys. 83 33
Google Scholar
[2] Yuan Z S, Chen Y A, Zhao B, Chen S, Schmiedmayer J, Pan J W 2008 Nature 454 1098
Google Scholar
[3] Duan L M, Lukin M D, Cirac J I, Zoller P 2001 Nature 414 413
Google Scholar
[4] Gisin N, Ribordy G, Tittle W, Zbinden H 2002 Rev. Mod. Phys. 74 145
Google Scholar
[5] Bao X H, Reingruber A, Dietrich P, Rui J, Dück A, Strassel T, Li L, Liu N L, Zhao B, Pan J W 2012 Nat. Phys. 8 517
Google Scholar
[6] Chen S, Chen Y A, Strassel T, Yuan Z S, Zhao B, Schmiedmayer J, Pan J W 2006 Phys. Rev. Lett. 97 173004
Google Scholar
[7] Chen S, Chen Y A, Zhao B, Yuan Z S, Schmiedmayer J, Pan J W 2007 Phys. Rev. Lett. 99 180505
Google Scholar
[8] Kuzmich A, Bowen W P, Boozer A D, Boca A, Chou C W, Duan L M, Kimble H J 2003 Nature 423 731
Google Scholar
[9] Matsukevich D N, Chaneliere T, Bhattacharya M, et al. 2005 Phys. Rev. Lett. 95 040405
Google Scholar
[10] Matsukevich D N, Chaneliere T, Jenkins S D, et al. 2006 Phys. Rev. Lett. 97 013601
Google Scholar
[11] Simon J, Tanji H, Thompson J K, Vuletic V 2007 Phys. Rev. Lett. 98 183601
Google Scholar
[12] Zhao B, Chen Y A, Bao X H, et al. 2008 Nat. Phys. 5 95
Google Scholar
[13] Zhao R, Dudin Y O, Jenkins S D, et al. 2008 Nat. Phys. 5 100
Google Scholar
[14] de Riedmatten H, Laurat J, Chou C W, et al. 2006 Phys. Rev. Lett. 97 113603
Google Scholar
[15] Matsukevich D N, Chaneliere T, Jenkins S D, Lan S Y, Kennedy T A, Kuzmich A 2006 Phys. Rev. Lett. 96 030405
Google Scholar
[16] Yang S J, Wang X J, Li J, Rui J, Bao X H, Pan J W 2015 Phys. Rev. Lett. 114 210501
Google Scholar
[17] Korzh B, Lim C C W, Houlmann R, et al. 2015 Nat. Photonics 9 163
Google Scholar
[18] Yin H L, Chen T Y, Yu Z W, et al. 2016 Phys. Rev. Lett. 117 190501
Google Scholar
[19] Collins M J, Xiong C, Rey I H, et al. 2013 Nat. Commun. 4 2582
Google Scholar
[20] Xiong C, Zhang X, Liu Z, et al. 2016 Nat. Commun. 7 10853
Google Scholar
[21] Tian L, Xu Z, Chen L, Ge W, Yuan H, Wen Y, Wang S, Li S, Wang H 2017 Phys. Rev. Lett. 119 130505
Google Scholar
[22] Wen Y, Zhou P, Xu Z, Yuan L, Zhang H, Wang S, Tian L, Li S, Wang H 2019 Phys. Rev. A 100 012342
Google Scholar
[23] Simon C, de Riedmatten H, Afzelius M 2010 Phys. Rev. A 82 010304(R
Google Scholar
[24] Heller L, Farrera P, Heinze G, de Riedmatten H 2020 Phys. Rev. Lett. 124 210504
Google Scholar
-
图 1
${}^{87}{\rm{Rb}}$ 实验能级图 (a)表示SRS中的写过程, W表示写光光场,${\sigma ^ + }$ (${\sigma ^ - }$ )代表左(右)旋圆偏振的Stokes光子Fig. 1. Relevant
${}^{87}{\rm{Rb}}$ atomic levels. (a) is the writing process of the SRS process, The coupling light field are writing light field(W),${\sigma ^ + }$ (${\sigma ^ - }$ ) represents left (right) polarization of Stokes.
图 2 实验装置图. 其中PZT代表压电陶瓷; CM表示腔镜; BS表示分束镜; Filter表示标准具滤波器;
$\lambda /4$ ,$\lambda /2$ 分别代表四分之一玻片和二分之一玻片; PBS为偏振分束棱镜; PD表示单光子探测器Fig. 2. Experimental setup. PZT represents the piezoelectric ceramic transducer; CM, cavity mirror; BS, beam splitter; Filter, F-P etalon;
$\lambda /4$ ,$\lambda /2$ , quarter wave plate and half wave plate; PBS, polarization beam splitter; PD, single photon detector.
图 3 实验时序图. 图中Cleaning为态制备过程, Write代表写过程, Locking表示腔锁定时序, MOT代表冷原子俘获过程
Fig. 3. Time sequence of experimental cycle. Cleaning, the state cleaning process; Write, the writing process; Locking, the locking cavity process; and MOT, the cold atom preparation process.
图 4 有无驻波腔时激发率随写光功率的变化对比
Fig. 4. Excitation probability as the function of power of write light field with cavity and without cavity.
-
[1] Sangouard N, Simon C, de Riedmatten H, Gisin N 2011 Rev. Mod. Phys. 83 33
Google Scholar
[2] Yuan Z S, Chen Y A, Zhao B, Chen S, Schmiedmayer J, Pan J W 2008 Nature 454 1098
Google Scholar
[3] Duan L M, Lukin M D, Cirac J I, Zoller P 2001 Nature 414 413
Google Scholar
[4] Gisin N, Ribordy G, Tittle W, Zbinden H 2002 Rev. Mod. Phys. 74 145
Google Scholar
[5] Bao X H, Reingruber A, Dietrich P, Rui J, Dück A, Strassel T, Li L, Liu N L, Zhao B, Pan J W 2012 Nat. Phys. 8 517
Google Scholar
[6] Chen S, Chen Y A, Strassel T, Yuan Z S, Zhao B, Schmiedmayer J, Pan J W 2006 Phys. Rev. Lett. 97 173004
Google Scholar
[7] Chen S, Chen Y A, Zhao B, Yuan Z S, Schmiedmayer J, Pan J W 2007 Phys. Rev. Lett. 99 180505
Google Scholar
[8] Kuzmich A, Bowen W P, Boozer A D, Boca A, Chou C W, Duan L M, Kimble H J 2003 Nature 423 731
Google Scholar
[9] Matsukevich D N, Chaneliere T, Bhattacharya M, et al. 2005 Phys. Rev. Lett. 95 040405
Google Scholar
[10] Matsukevich D N, Chaneliere T, Jenkins S D, et al. 2006 Phys. Rev. Lett. 97 013601
Google Scholar
[11] Simon J, Tanji H, Thompson J K, Vuletic V 2007 Phys. Rev. Lett. 98 183601
Google Scholar
[12] Zhao B, Chen Y A, Bao X H, et al. 2008 Nat. Phys. 5 95
Google Scholar
[13] Zhao R, Dudin Y O, Jenkins S D, et al. 2008 Nat. Phys. 5 100
Google Scholar
[14] de Riedmatten H, Laurat J, Chou C W, et al. 2006 Phys. Rev. Lett. 97 113603
Google Scholar
[15] Matsukevich D N, Chaneliere T, Jenkins S D, Lan S Y, Kennedy T A, Kuzmich A 2006 Phys. Rev. Lett. 96 030405
Google Scholar
[16] Yang S J, Wang X J, Li J, Rui J, Bao X H, Pan J W 2015 Phys. Rev. Lett. 114 210501
Google Scholar
[17] Korzh B, Lim C C W, Houlmann R, et al. 2015 Nat. Photonics 9 163
Google Scholar
[18] Yin H L, Chen T Y, Yu Z W, et al. 2016 Phys. Rev. Lett. 117 190501
Google Scholar
[19] Collins M J, Xiong C, Rey I H, et al. 2013 Nat. Commun. 4 2582
Google Scholar
[20] Xiong C, Zhang X, Liu Z, et al. 2016 Nat. Commun. 7 10853
Google Scholar
[21] Tian L, Xu Z, Chen L, Ge W, Yuan H, Wen Y, Wang S, Li S, Wang H 2017 Phys. Rev. Lett. 119 130505
Google Scholar
[22] Wen Y, Zhou P, Xu Z, Yuan L, Zhang H, Wang S, Tian L, Li S, Wang H 2019 Phys. Rev. A 100 012342
Google Scholar
[23] Simon C, de Riedmatten H, Afzelius M 2010 Phys. Rev. A 82 010304(R
Google Scholar
[24] Heller L, Farrera P, Heinze G, de Riedmatten H 2020 Phys. Rev. Lett. 124 210504
Google Scholar
下载:
计量
- 文章访问数: 5393
- PDF下载量: 122
- 被引次数: 0
