基于通信序列熵的复杂网络传输容量

马金龙; 张俊峰; 张冬雯; 张红斌

doi:10.7498/aps.70.20201300

摘要

网络的传输性能在一定程度上依赖于网络的拓扑结构. 本文从结构信息的角度分析复杂网络的传输动力学行为, 寻找影响网络传输容量的信息结构测度指标. 通信序列熵可以有效地量化网络的整体结构信息, 为了表征网络整体传输能力, 把通信序列熵引入到复杂网络传输动力学分析中, 研究网络的通信序列熵与传输性能之间的关联特性, 分析这种相关性存在的内在机理. 分别在BA无标度和WS小世界网络模型上进行仿真, 结果显示: 网络的通信序列熵与其传输容量存在密切关联性, 随着通信序列熵的增加, 网络拓扑结构的均匀性随之增强, 传输容量明显增加. 网络的传输容量是通信序列熵的单调递增函数, 与通信序列熵成正关联关系. 通信序列熵可有效评估网络的传输容量, 本结论可为设计高传输容量网络提供理论依据.

关键词:

Abstract

The transmission performance of the network depends to a certain extent on the topology of the network. This article analyzes the traffic dynamics of complex networks from the perspective of structural information, and looks for information structure measurement indicators that affect network traffic capacity. Existing research shows that the communicability sequence entropy of complex networks can effectively quantify the overall structure of the network. Based on this measurement, the difference between networks can be effectively quantified, and the connotation of sequence entropy of communicability can be explained. Communication sequence entropy can effectively quantify the overall structure information of the network. In order to characterize the overall traffic capacity of the network, the communication sequence entropy is introduced into the phenomenon of complex network congestion, the correlation between the network communication sequence entropy and the transmission performance is studied, and the internal mechanism of this correlation is analyzed. Simulations in BA scale-free network model and WS small-world network model show that the communication sequence entropy of the network is closely related to its traffic capacity. As the communication sequence entropy increases, the uniformity of the network topology will increase, and the traffic capacity will increase significantly. The traffic capacity of the network is a monotonically increasing function of the entropy of the communication sequence, and is positively correlated with the entropy of the communication sequence. The communication sequence entropy of the network can effectively evaluate the traffic capacity of the network. This conclusion can provide a theoretical basis for the design of a high traffic capacity network and help provide an effective strategy for the design of the high traffic capacity of the network, which can be optimized by increasing the communication sequence entropy.

Keywords:

作者及机构信息

河北科技大学信息科学与工程学院, 石家庄　050018

通信作者: 马金龙, mzjinlong@163.com

基金项目: 2020年度河北省军民融合发展研究课题(批准号: HB20JMRH008)、教育部人文社科基金(批准号: 19YJAZH069)、国家自然科学基金(批准号: 61672206, 61572170)、河北省科技支撑计划(批准号: 18210109D, 20310701D)和河北省高层次人才资助项目(批准号: A2016002015)资助的课题

Authors and contacts

School of Information Science and Engineering, Hebei University of Science and Technology, Shijiazhuang 050018, China

Corresponding author: Ma Jin-Long, mzjinlong@163.com

Funds: Project supported by the 2020 Military-Civilian Integration Development Research Project of Hebei Province, China (Grant No. HB20JMRH008), the Humanities and Social Sciences Fund of the Ministry of Education of China (Grant No. 19YJAZH069), the National Natural Science Foundation of China (Grant Nos. 61672206, 61572170), the Science and Technology Support Program of Hebei Province, China (Grant Nos. 18210109D, 20310701D), and the High Level Talent Funding Project of Hebei Province, China (Grant No. A2016002015)

文章全文 : translate this paragraph

参考文献

[1]	Wu G H, Yang H J, Pan J H 2018 Mod. Phys. Lett. B 9 1850137 Google Scholar
[2]	Kumari S, Singh A 2019 Mod. Phys. Lett. B 1 13 Google Scholar
[3]	Jiang L R, Jin X Y, Xia Y X, Ouyang B, Wu D P, Chen X 2014 Int. J. Distrib. Sens. Netw. 1155 764698 Google Scholar
[4]	Tu H C, Xia Y X, Wu J J, Zhou X 2019 Physica A 9 17
[5]	Bianchin G, Pasqualetti F 2020 IEEE Trans. Intell. Transp. 3013 3024 Google Scholar
[6]	Serok N, Levy O, Havlin S, Blumenfeld-Lieberthal E 2019 EPB: Urban Analytics and City Science 1362 1376 Google Scholar
[7]	Li H J, Wang H, Chen L N 2014 Europhys. Lett. 108 68009 Google Scholar
[8]	Xiang J, Wang Z Z, Li H J, Zhang Y, Li F, Dong L P, Li J M, Guo L J 2017 J. Stat. Mech. Theory Exp. 5 053213 Google Scholar
[9]	Chen G, Kong R, Wang Y X 2020 Physica A 540 123002 Google Scholar
[10]	Barabási A L, Albert R 1999 Science 509 512 Google Scholar
[11]	Watts D J, Strogatz S H 1998 Nature 440 442
[12]	Tan F, Wu J J, Xia Y X, Tse C K 2014 Phys. Rev. E 89 062813 Google Scholar
[13]	杨卓璇, 马源培, 李慧嘉 2020 聊城大学学报 (自然科学版) 12 26 Yang Z X, Ma Y P, Li H J 2020 Journal of Liaocheng University (Social Science Edition) 12 26
[14]	马源培, 杨卓璇, 李慧嘉 2020 聊城大学学报(自然科学版) 26 32 Ma Y P, Yang Z X, Li H J 2020 Journal of Liaocheng University (Social Science Edition) 26 32
[15]	Guimerà R, Díaz-Guilera A, Vega-Redondo F, Cabrales A, Arenas A 2002 Phys. Rev. Lett. 89 248701 Google Scholar
[16]	Zhao L, Lai Y C, Park K, Ye N 2005 Phys. Rev. E 71 026125 Google Scholar
[17]	孙磊, 李荣, 靳聪, 陈孝国 2015 科技导报 86 89 Google Scholar Sun L, Li R, Jin C, Chen X G 2015 Science and Technology Review 86 89 Google Scholar
[18]	Chen Z H, Wu J J, Rong Z H, Tse C K 2018 Physica A 191 201
[19]	Cai J, Wang Y, Liu Y, Luo J Z, Wei W G, Xu X P 2018 Future Gener. Comp. Syst. 765 771 Google Scholar
[20]	蔡君, 余顺争 2013 62 058901 Google Scholar Cai J, Yu S Z 2013 Acta Phys. Sin. 62 058901 Google Scholar
[21]	Chen R B, Cui W, Pu C L, Li J, Ji B, Gakis K, Pardalos P M 2018 Physica A 524 532 Google Scholar
[22]	Cui J B, Xiang J, Liu Y, Hu K, Tang Y 2020 J. Phys. Soc. Jpn. 89 014802 Google Scholar
[23]	DuBois T, Eubank S, Srinivasan A 2012 Electron. J. Comb. 1 19
[24]	Hu K, Liu C, Hu T, Tang Y 2010 J. Phys. A: Math. Theor. 43 175101 Google Scholar
[25]	Huang W, Tommy W S C 2010 J. Stat. Mech. Theory Exp. 1 12 Google Scholar
[26]	Jiang Z Y, Liang M G, Guo D C 2011 Int. J. Mod. Phys. C 1211 1226 Google Scholar
[27]	Jiang Z Y, Liang M G, An W J 2014 Physica A 379 385 Google Scholar
[28]	Jiang Z Y, Liang M G, Guo D C 2013 Mod. Phys. Lett. B 8 1350056 Google Scholar
[29]	陈乐瑞, 潘秋萍, 孔金生 2016 计算机系统应用 145 148 Google Scholar Chen L R, Pan Q P, Kong J S 2016 Computer Systems and Applications 145 148 Google Scholar
[30]	孙中悦, 贾兴华 2017 计算机工程 75 78 Google Scholar Sun Z Y, Jia X H 2017 Computer Engineering 75 78 Google Scholar
[31]	Wang D, Liu E W, Liu D, Qu X Y, Ma R F, Wang P, Liu X C 2015 IEEE Commun. Lett. 2110 2113 Google Scholar
[32]	Zhang G Q, Wang D, Li G J 2007 Phys. Rev. E 76 017101 Google Scholar
[33]	Zhang S, Liang M G, Jiang Z Y, Wu J J 2014 Int. J. Mod. Phys. C 6 1450014 Google Scholar
[34]	Zhang Z H, Liu S Y, Yang Y Q, Bai Y G 2019 Cluster Comput. 7687 7694
[35]	申弢, 黄树红, 韩守木, 杨叔子 2001 机械工程学报 94 98 Shen T, Huang S H, Han S M, Yang S Z 2001 Journal of Mechanical Engineering 94 98
[36]	赵荣珍, 张优云 2004 振动、测试与诊断 180 187 Zhao R Z, Zhang Y Y 2004 Journal of Vibration, Measurement and Diagnosis 180 187
[37]	王治忠, 钱龙龙, 韩闯, 师丽 2020 计算机应用 608 615 Google Scholar Wang Z Z, Qian L L, Han C, Shi L 2020 Journal of Computer Applications 608 615 Google Scholar
[38]	Wang B, Tang H W, Guo C H, Xiu Z L 2006 Physica A 363 591 Google Scholar
[39]	吴俊, 谭跃进, 邓宏钟, 朱大智 2007 系统工程理论与实践 101 105 Wu J, Tan Y J, Deng H Z, Zhu D Z 2007 Syst. Engin. Theo. Prac. 101 105
[40]	蔡萌, 杜海峰, 任义科, 费尔德曼 2011 60 110513 Google Scholar Cai M, Du H F, Ren Y K, Marcus W F 2011 Acta Phys. Sin. 60 110513 Google Scholar
[41]	蔡萌, 杜海峰, 费尔德曼 2014 63 060504 Google Scholar Cai M, Du H F, Marcus W F 2014 Acta Phys. Sin. 63 060504 Google Scholar
[42]	胡钢, 徐翔, 高浩, 过秀成 2020 系统工程理论与实践 714 725 Google Scholar Hu G, Xu X, Gao H, Guo X C 2020 Syst. Engin. Theo. Prac. 714 725 Google Scholar
[43]	Chen D, Shi D D, Qin M, Xu S M, Pan G J 2018 Phys. Rev. E 98 012319 Google Scholar
[44]	陈单, 石丹丹, 潘贵军 2019 物理学报 68 118901 Google Scholar Chen D, Shi D D, Pan G J 2019 Acta Phys. Sin. 68 118901 Google Scholar
[45]	石丹丹, 陈单, 龙慧敏, 王承科, 潘贵军 2019 中国科学:物理学力学天文学 49 070502 Google Scholar Shi D D, Chen D, Long H M, Wang C K, Pan G J 2019 Science China Physics, Mechanics and Astronomy 49 070502 Google Scholar
[46]	Estrada E, Hatano N 2008 Phys. Rev. E 77 036111 Google Scholar
[47]	Estrada E 2012 Linear Algebra Appl. 4317 4328 Google Scholar
[48]	Estrada E, Hatano N, Benzi M 2012 Phys. Rep. 89 119 Google Scholar
[49]	Mukherjee G, Manna S S 2005 Phys. Rev. E 71 066108 Google Scholar
[50]	Zhou T, Yan G, Wang B H, Fu Z Q, Hu B, Zhu C P, Wang W X 2006 Dyam. Cont. Dis. Ser. B 13 463
[51]	Barthélemy M 2004 EurPhys. J. B 163 168 Google Scholar
[52]	Holme P, Kim B J, Yoon C N, Han S K 2002 Phys. Rev. E 65 066109 Google Scholar
[53]	Jiang Z Y, Liang M G 2012 Mod. Phys. Lett. B 29 1250195 Google Scholar
[54]	Yan G, Zhou T, Hu B, Fu Z Q, Wang B H 2006 Phys. Rev. E 73 046108 Google Scholar

施引文献

图 1 网络的通信序列熵S_N与网络的度分布P(k)之间的关系图　(a) BA无标度网络; (b) WS小世界网络

Fig. 1. Rrelationship between the network’s communication sequence entropy S_N and the network’s degree distribution P(k): (a) BA scale-free network; (b) WS small world network.

下载: 全尺寸图片幻灯片

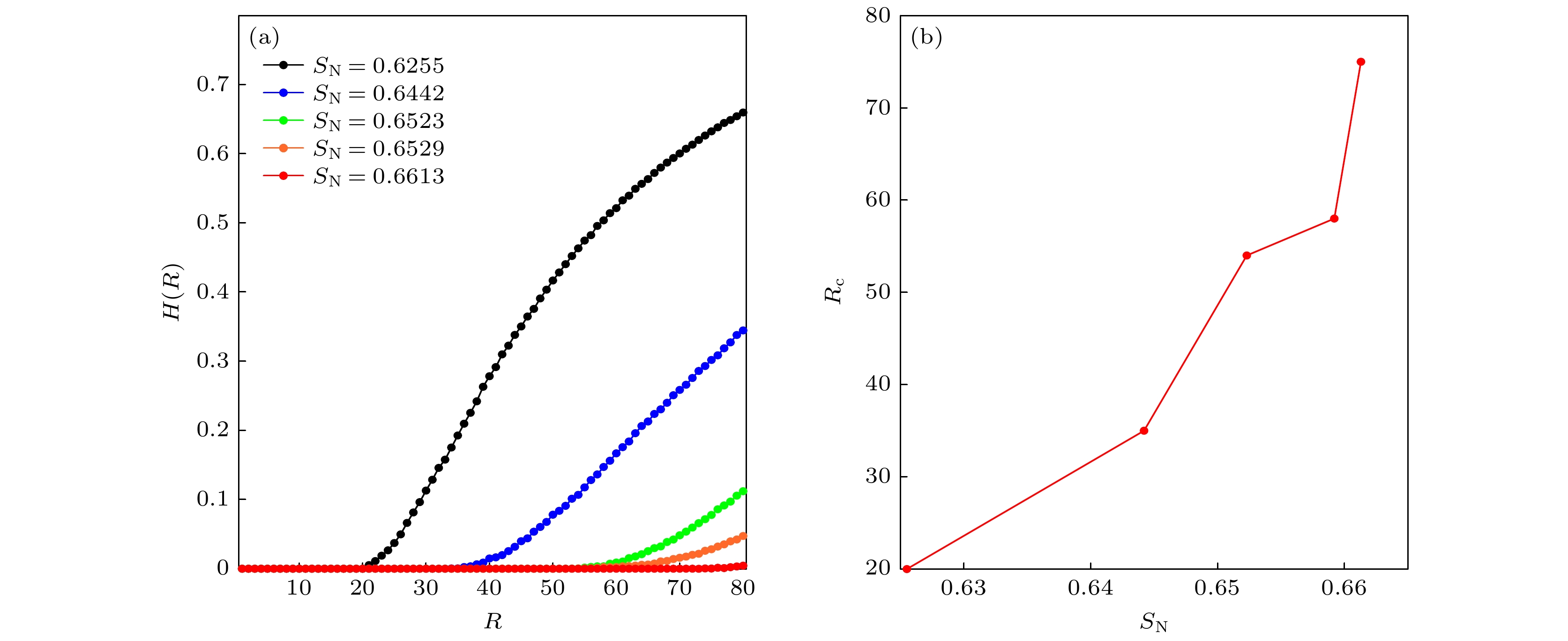
图 2 (a)不同的通信序列熵的BA无标度网络下, 有序参数H(R)与数据包生成率R的关系; (b) BA无标度网络通信序列熵$S_{\rm N}$与传输容量$R_{\rm c}$的关系. 采用的路由策略为有效路由策略

Fig. 2. (a) Relationship between the order parameter H(R) and the packet generation rate R under BA scale-free network with different communication sequence entropy; (b) relationship between BA scale-free network communication sequence entropy$S_{\rm N}$ and traffic capacity $R_{\rm c}$. The routing strategy adopted is an effective routing strategy.

下载: 全尺寸图片幻灯片

图 3 (a)不同的通信序列熵的WS小世界网络下, 有序参数H(R)与数据包生成率R的关系; (b) WS小世界网络通信序列熵$S_{\rm N}$与传输容量$R_{\rm c}$的关系. 采用的路由策略为有效路由策略

Fig. 3. (a) Relationship between the order parameters $H(R)$and the packet generation rate R under the WS small world network with different communication sequence entropy; (b) relationship between WS small world network communication sequence entropy$S_{\rm N}$ and traffic capacity $R_{\rm c}$. The routing strategy adopted is an effective routing strategy.

下载: 全尺寸图片幻灯片

图 4 数据包负载 (traffic load) 在网络中节点度值上的分布情况　(a) BA无标度网络; (b) WS小世界网络

Fig. 4. Distribution of traffic load on degree value of nodes in the network: (a) BA scale-free network; (b) WS small world network.

下载: 全尺寸图片幻灯片

图 5 网络的通信序列熵$S_{\rm N}$与平均路径长度$\left\langle {L} \right\rangle $的关系　(a) BA无标度网络; (b) WS小世界网络

Fig. 5. Relationship between communication sequence entropy S_N and average path length$\left\langle {L} \right\rangle $ in the network: (a) BA scale-free network; (b) WS small world network.

下载: 全尺寸图片幻灯片

图 6 网络的通信序列熵$S_{\rm N}$与节点的最大介数$B_{\rm {max}}$的关系　(a) BA无标度网络; (b) WS小世界网络

Fig. 6. Relationship between communication sequence entropy $S_{\rm N}$ and the maximum betweenness of nodes $B_{\rm {max}}$ in the network: (a) BA scale-free network; (b) WS small world network.

下载: 全尺寸图片幻灯片

map

[1]	Wu G H, Yang H J, Pan J H 2018 Mod. Phys. Lett. B 9 1850137 Google Scholar
[2]	Kumari S, Singh A 2019 Mod. Phys. Lett. B 1 13 Google Scholar
[3]	Jiang L R, Jin X Y, Xia Y X, Ouyang B, Wu D P, Chen X 2014 Int. J. Distrib. Sens. Netw. 1155 764698 Google Scholar
[4]	Tu H C, Xia Y X, Wu J J, Zhou X 2019 Physica A 9 17
[5]	Bianchin G, Pasqualetti F 2020 IEEE Trans. Intell. Transp. 3013 3024 Google Scholar
[6]	Serok N, Levy O, Havlin S, Blumenfeld-Lieberthal E 2019 EPB: Urban Analytics and City Science 1362 1376 Google Scholar
[7]	Li H J, Wang H, Chen L N 2014 Europhys. Lett. 108 68009 Google Scholar
[8]	Xiang J, Wang Z Z, Li H J, Zhang Y, Li F, Dong L P, Li J M, Guo L J 2017 J. Stat. Mech. Theory Exp. 5 053213 Google Scholar
[9]	Chen G, Kong R, Wang Y X 2020 Physica A 540 123002 Google Scholar
[10]	Barabási A L, Albert R 1999 Science 509 512 Google Scholar
[11]	Watts D J, Strogatz S H 1998 Nature 440 442
[12]	Tan F, Wu J J, Xia Y X, Tse C K 2014 Phys. Rev. E 89 062813 Google Scholar
[13]	杨卓璇, 马源培, 李慧嘉 2020 聊城大学学报 (自然科学版) 12 26 Yang Z X, Ma Y P, Li H J 2020 Journal of Liaocheng University (Social Science Edition) 12 26
[14]	马源培, 杨卓璇, 李慧嘉 2020 聊城大学学报(自然科学版) 26 32 Ma Y P, Yang Z X, Li H J 2020 Journal of Liaocheng University (Social Science Edition) 26 32
[15]	Guimerà R, Díaz-Guilera A, Vega-Redondo F, Cabrales A, Arenas A 2002 Phys. Rev. Lett. 89 248701 Google Scholar
[16]	Zhao L, Lai Y C, Park K, Ye N 2005 Phys. Rev. E 71 026125 Google Scholar
[17]	孙磊, 李荣, 靳聪, 陈孝国 2015 科技导报 86 89 Google Scholar Sun L, Li R, Jin C, Chen X G 2015 Science and Technology Review 86 89 Google Scholar
[18]	Chen Z H, Wu J J, Rong Z H, Tse C K 2018 Physica A 191 201
[19]	Cai J, Wang Y, Liu Y, Luo J Z, Wei W G, Xu X P 2018 Future Gener. Comp. Syst. 765 771 Google Scholar
[20]	蔡君, 余顺争 2013 62 058901 Google Scholar Cai J, Yu S Z 2013 Acta Phys. Sin. 62 058901 Google Scholar
[21]	Chen R B, Cui W, Pu C L, Li J, Ji B, Gakis K, Pardalos P M 2018 Physica A 524 532 Google Scholar
[22]	Cui J B, Xiang J, Liu Y, Hu K, Tang Y 2020 J. Phys. Soc. Jpn. 89 014802 Google Scholar
[23]	DuBois T, Eubank S, Srinivasan A 2012 Electron. J. Comb. 1 19
[24]	Hu K, Liu C, Hu T, Tang Y 2010 J. Phys. A: Math. Theor. 43 175101 Google Scholar
[25]	Huang W, Tommy W S C 2010 J. Stat. Mech. Theory Exp. 1 12 Google Scholar
[26]	Jiang Z Y, Liang M G, Guo D C 2011 Int. J. Mod. Phys. C 1211 1226 Google Scholar
[27]	Jiang Z Y, Liang M G, An W J 2014 Physica A 379 385 Google Scholar
[28]	Jiang Z Y, Liang M G, Guo D C 2013 Mod. Phys. Lett. B 8 1350056 Google Scholar
[29]	陈乐瑞, 潘秋萍, 孔金生 2016 计算机系统应用 145 148 Google Scholar Chen L R, Pan Q P, Kong J S 2016 Computer Systems and Applications 145 148 Google Scholar
[30]	孙中悦, 贾兴华 2017 计算机工程 75 78 Google Scholar Sun Z Y, Jia X H 2017 Computer Engineering 75 78 Google Scholar
[31]	Wang D, Liu E W, Liu D, Qu X Y, Ma R F, Wang P, Liu X C 2015 IEEE Commun. Lett. 2110 2113 Google Scholar
[32]	Zhang G Q, Wang D, Li G J 2007 Phys. Rev. E 76 017101 Google Scholar
[33]	Zhang S, Liang M G, Jiang Z Y, Wu J J 2014 Int. J. Mod. Phys. C 6 1450014 Google Scholar
[34]	Zhang Z H, Liu S Y, Yang Y Q, Bai Y G 2019 Cluster Comput. 7687 7694
[35]	申弢, 黄树红, 韩守木, 杨叔子 2001 机械工程学报 94 98 Shen T, Huang S H, Han S M, Yang S Z 2001 Journal of Mechanical Engineering 94 98
[36]	赵荣珍, 张优云 2004 振动、测试与诊断 180 187 Zhao R Z, Zhang Y Y 2004 Journal of Vibration, Measurement and Diagnosis 180 187
[37]	王治忠, 钱龙龙, 韩闯, 师丽 2020 计算机应用 608 615 Google Scholar Wang Z Z, Qian L L, Han C, Shi L 2020 Journal of Computer Applications 608 615 Google Scholar
[38]	Wang B, Tang H W, Guo C H, Xiu Z L 2006 Physica A 363 591 Google Scholar
[39]	吴俊, 谭跃进, 邓宏钟, 朱大智 2007 系统工程理论与实践 101 105 Wu J, Tan Y J, Deng H Z, Zhu D Z 2007 Syst. Engin. Theo. Prac. 101 105
[40]	蔡萌, 杜海峰, 任义科, 费尔德曼 2011 60 110513 Google Scholar Cai M, Du H F, Ren Y K, Marcus W F 2011 Acta Phys. Sin. 60 110513 Google Scholar
[41]	蔡萌, 杜海峰, 费尔德曼 2014 63 060504 Google Scholar Cai M, Du H F, Marcus W F 2014 Acta Phys. Sin. 63 060504 Google Scholar
[42]	胡钢, 徐翔, 高浩, 过秀成 2020 系统工程理论与实践 714 725 Google Scholar Hu G, Xu X, Gao H, Guo X C 2020 Syst. Engin. Theo. Prac. 714 725 Google Scholar
[43]	Chen D, Shi D D, Qin M, Xu S M, Pan G J 2018 Phys. Rev. E 98 012319 Google Scholar
[44]	陈单, 石丹丹, 潘贵军 2019 物理学报 68 118901 Google Scholar Chen D, Shi D D, Pan G J 2019 Acta Phys. Sin. 68 118901 Google Scholar
[45]	石丹丹, 陈单, 龙慧敏, 王承科, 潘贵军 2019 中国科学:物理学力学天文学 49 070502 Google Scholar Shi D D, Chen D, Long H M, Wang C K, Pan G J 2019 Science China Physics, Mechanics and Astronomy 49 070502 Google Scholar
[46]	Estrada E, Hatano N 2008 Phys. Rev. E 77 036111 Google Scholar
[47]	Estrada E 2012 Linear Algebra Appl. 4317 4328 Google Scholar
[48]	Estrada E, Hatano N, Benzi M 2012 Phys. Rep. 89 119 Google Scholar
[49]	Mukherjee G, Manna S S 2005 Phys. Rev. E 71 066108 Google Scholar
[50]	Zhou T, Yan G, Wang B H, Fu Z Q, Hu B, Zhu C P, Wang W X 2006 Dyam. Cont. Dis. Ser. B 13 463
[51]	Barthélemy M 2004 EurPhys. J. B 163 168 Google Scholar
[52]	Holme P, Kim B J, Yoon C N, Han S K 2002 Phys. Rev. E 65 066109 Google Scholar
[53]	Jiang Z Y, Liang M G 2012 Mod. Phys. Lett. B 29 1250195 Google Scholar
[54]	Yan G, Zhou T, Hu B, Fu Z Q, Wang B H 2006 Phys. Rev. E 73 046108 Google Scholar

[1]	汪亭亭, 梁宗文, 张若曦. 基于信息熵与迭代因子的复杂网络节点重要性评价方法. , 2023, 72(4): 048901. doi: 10.7498/aps.72.20221878
[2]	林泓, 夏永祥, 蒋路茸. 基于最短路径长度的空间网络路由. , 2022, 71(6): 068901. doi: 10.7498/aps.71.20211621
[3]	马金龙, 杜长峰, 隋伟, 许向阳. 基于耦合强度的双层网络数据传输能力. , 2020, 69(18): 188901. doi: 10.7498/aps.69.20200181
[4]	汪丽娜, 成媛媛, 臧臣瑞. 基于seasonal-trend-loess方法的符号化时间序列网络. , 2019, 68(23): 238901. doi: 10.7498/aps.68.20190794
[5]	陈单, 石丹丹, 潘贵军. 复杂网络电输运性能与通信序列熵之间的关联. , 2019, 68(11): 118901. doi: 10.7498/aps.68.20190230
[6]	李勇军, 尹超, 于会, 刘尊. 基于最大熵模型的微博传播网络中的链路预测. , 2016, 65(2): 020501. doi: 10.7498/aps.65.020501
[7]	李世宝, 娄琳琳, 陈瑞祥, 洪利. 一种复杂网络路由策略的普适优化算法. , 2014, 63(2): 028901. doi: 10.7498/aps.63.028901
[8]	刘伟彦, 刘斌. 基于局部路由策略的复杂网络拥塞控制. , 2014, 63(24): 248901. doi: 10.7498/aps.63.248901
[9]	蔡君, 余顺争. 一种有效提高无标度网络负载容量的管理策略. , 2013, 62(5): 058901. doi: 10.7498/aps.62.058901
[10]	周婷婷, 金宁德, 高忠科, 罗跃斌. 基于有限穿越可视图的时间序列网络模型. , 2012, 61(3): 030506. doi: 10.7498/aps.61.030506
[11]	高忠科, 金宁德, 杨丹, 翟路生, 杜萌. 多元时间序列复杂网络流型动力学分析. , 2012, 61(12): 120510. doi: 10.7498/aps.61.120510
[12]	高湘昀, 安海忠, 方伟. 基于复杂网络的时间序列双变量相关性波动研究. , 2012, 61(9): 098902. doi: 10.7498/aps.61.098902
[13]	王丹, 金小峥. 可调聚类系数加权无标度网络建模及其拥塞问题研究. , 2012, 61(22): 228901. doi: 10.7498/aps.61.228901
[14]	刘刚, 李永树. 基于引力场理论的复杂网络路由选择策略研究. , 2012, 61(24): 248901. doi: 10.7498/aps.61.248901
[15]	刘刚, 李永树. 基于引力约束的复杂网络拥塞问题研究. , 2012, 61(10): 108901. doi: 10.7498/aps.61.108901
[16]	宋玉蓉, 蒋国平. 具有非均匀传输和抗攻击差异的网络病毒传播模型. , 2010, 59(11): 7546-7551. doi: 10.7498/aps.59.7546
[17]	宋青松, 冯祖仁, 李人厚. 用于混沌时间序列预测的多簇回响状态网络. , 2009, 58(7): 5057-5064. doi: 10.7498/aps.58.5057
[18]	李涛, 裴文江, 王少平. 无标度复杂网络负载传输优化策略. , 2009, 58(9): 5903-5910. doi: 10.7498/aps.58.5903
[19]	陈华良, 刘忠信, 陈增强, 袁著祉. 复杂网络的一种加权路由策略研究. , 2009, 58(9): 6068-6073. doi: 10.7498/aps.58.6068
[20]	王丹, 于灏, 井元伟, 姜囡, 张嗣瀛. 基于感知流量算法的复杂网络拥塞问题研究. , 2009, 58(10): 6802-6808. doi: 10.7498/aps.58.6802

计量

文章访问数: 5977
PDF下载量: 141
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

基于通信序列熵的复杂网络传输容量