激光局域网络的混沌控制及并行队列同步

颜森林

doi:10.7498/aps.70.20201251

摘要

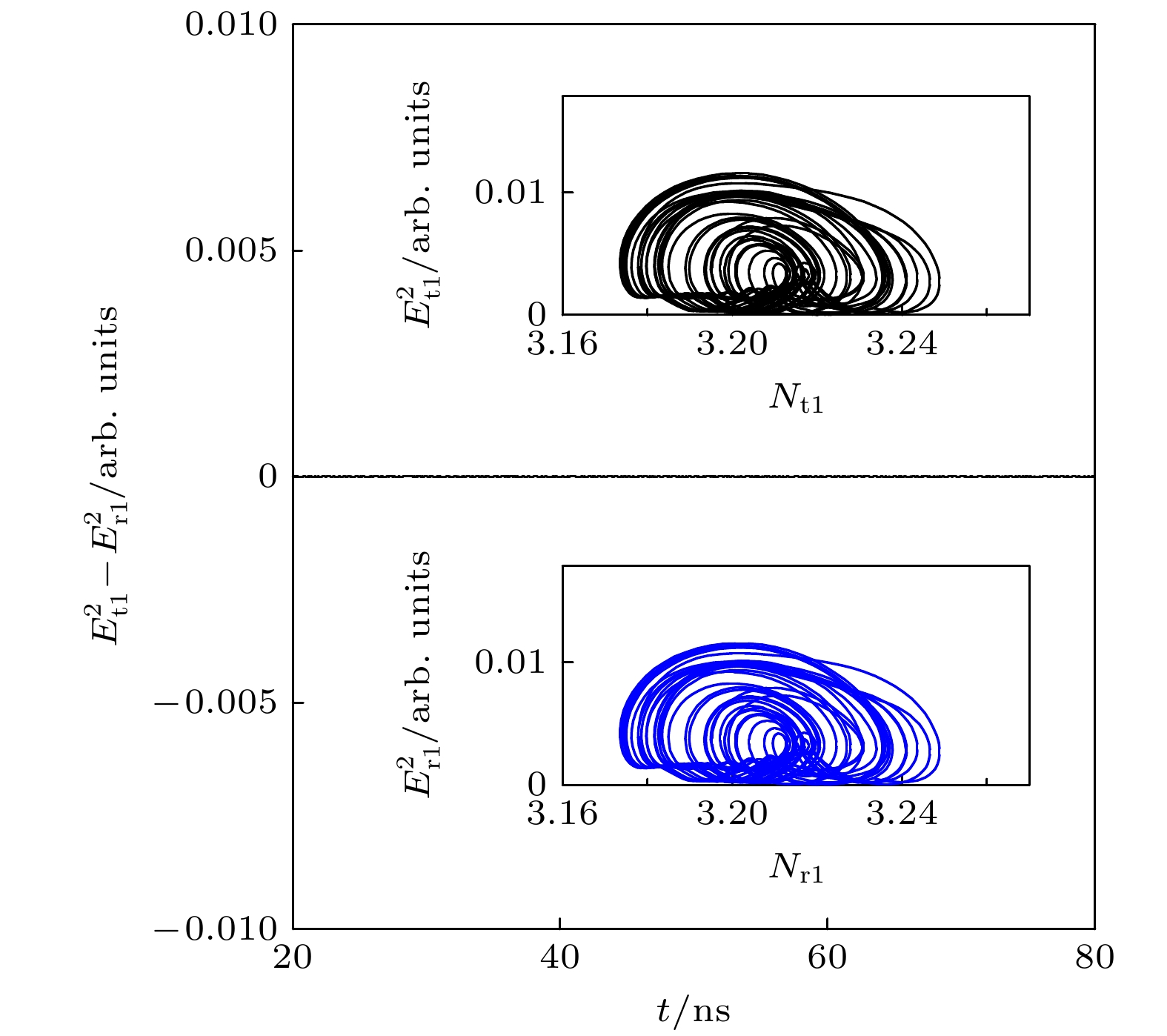
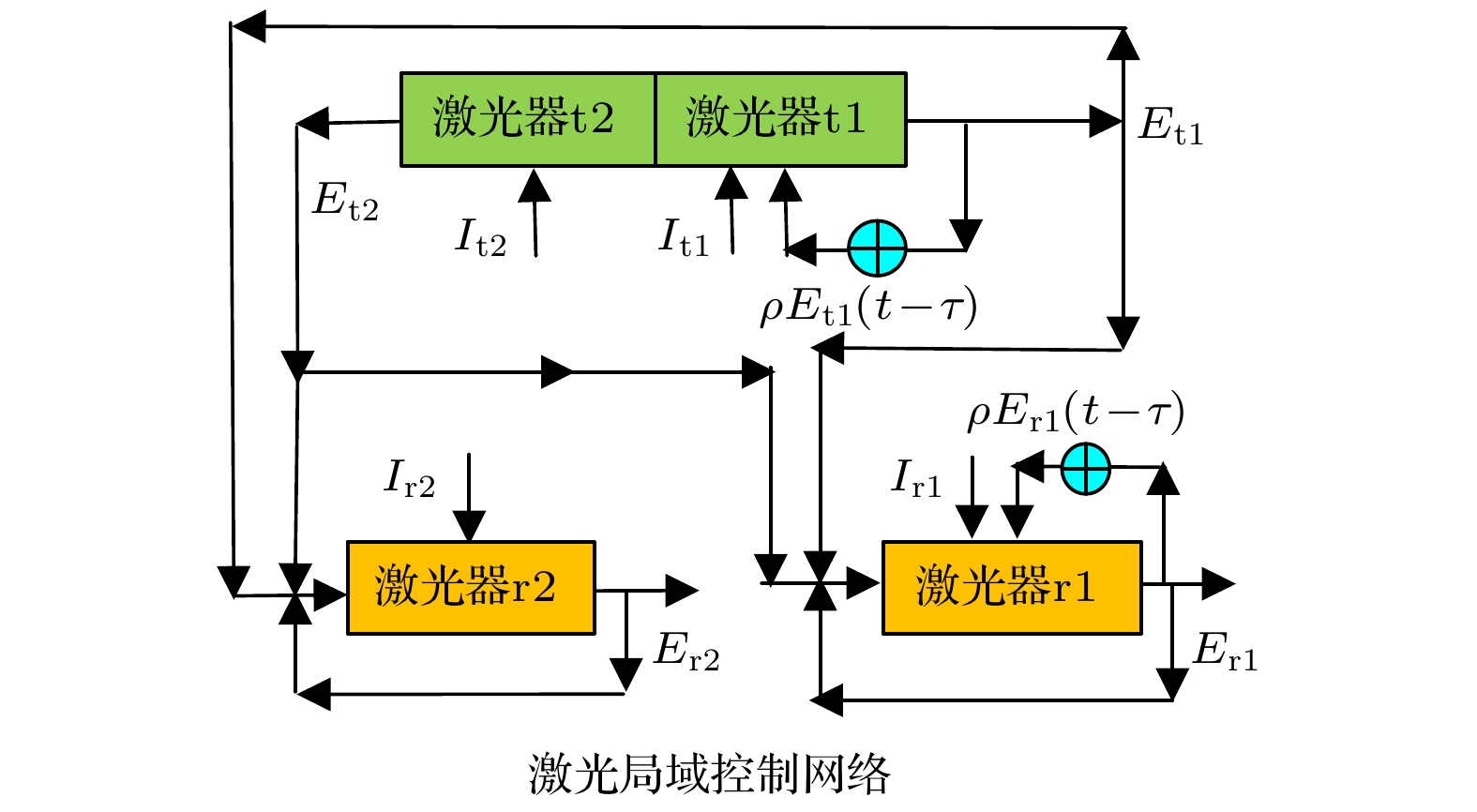
本文提出并研究了“单队列-双参数”光电延时反馈控制条件下的激光局域网络的混沌控制及串联的动力学行为的并行队列“交叉驱动-反馈”网络同步实现, 建立了该光学局域网络的数学物理控制模型. 通过含时延超越方程理论的分析, 预言了该光学局域网络是可以实现混沌控制的, 且网络两路结点队列是可以实现实时引导控制到多个类周期状态上的, 并通过并行队列同步方程理论证明并行串联队列同步是可以获得的. 结果发现在可控的激光局域网络两个并行串联队列光路上, 分别实现了网络队列结点的混沌控制并能够实现多个类周期的网络结点的并行串联队列同步, 实现了络网结点激光器的2周期、3周期、4周期等状态的并行队列同步, 以及其他多个类周期的队列并行同步和动态同步. 还发现了两个类周期并行队列网络同步控制区域. 本文还给出了激光局域网络“并行多点混沌载波同步发射及其在光学超宽带通信中应用”的一个案例并成功实现. 这是一种新型的激光混沌局域网络控制系统, 具有光局域网络光传送与光联接核心控制技术要素, 具有复杂动力学系统与网络的多变量、多空间维度及并行两路不同队列混沌控制技术特点, 还具有光网络超宽带通信功能等. 其研究结果对局域网络、光网络的控制与同步、激光技术以及混沌的研究具有重要的参考价值.

关键词:

混沌 /
控制 /
同步 /
局域网络 /
激光网络 /
周期

Abstract

In this work, we study the chaos-control and parallel queue synchronization of a laser local area network (LAN). We present and study specifically a “single-queue-double-parameter” method of the parallel series queue dynamic behavior synchronization of the controlled laser LAN under two optoelectronic delay feedback controllers, and establish the mathematical and physical model of the controlled laser LAN. The LAN node is composed of two space coupled lasers with different parameters and other two single lasers, where two lasers series produce two different parallel queues, which results in two different chains of LAN nodes. Optical LAN links are composed of two optical parallel-crossing paths and two photoelectric delay feedback controllers setting in two lasers of LAN, which creates a method of double-parameter control of LAN. Through the analysis of the stability theory of differential equation and the dynamic characteristic equation of coupled lasers of LAN, our mathematical theory demonstrates that the chaos-control of laser LAN can be achieved by two photoelectric delay feedback controllers adjusting photoelectric feedback levels and feedback delay time of one of the two coupled laser and another single laser, respectively. Making analysis of the stability theory of differential equation and the dynamic characteristic equation of LAN nodes in two queue chains, we demonstrate theoretically how to obtain synchronization in network nodes of the controlled LAN on two queue chains by controlling optical feedback levels, and by the photoelectric delay feedback controllers adjusting photoelectric feedback levels and feedback delay time, respectively. Using our numerical calculation of parallel queue synchronization, the node laser’s waveform and its phase space trajectory, we find that very lasers of network nodes of the controlled LAN can lead to the parallel queue synchronization of a double-period, a three-period, a four-period and other quasi-periods while these quasi-periodic synchronizations and dynamic synchronizations are controlled in two queue chains of LAN nodes when we let the photoelectric feedback level and the delay time shift on some parameters. We find also two controlled quasi-periodic parallel queue synchronization regions. This paper also presents an application case of laser LAN multi-point chaotic carrier synchronous emission and ultra-wideband communication. This is a new type of controlled laser LAN system, which has the core elements of optical LAN and the characteristics of multi-variable, multi-dimension and parallel queue chaos-control techniques of complex dynamic networks. It also has the function of optical network ultra-wideband communication. The results have important reference value for studying the LAN, optical network and its synchronization and control, laser technology and chaos.

Keywords:

作者及机构信息

颜森林

南京晓庄学院电子工程学院, 南京　211171

通信作者: 颜森林, senlinyan@163.com

Authors and contacts

Yan Sen-Lin

School of Electronic Engineering, Nanjing Xiaozhuang University, Nanjing 211171, China

Corresponding author: Yan Sen-Lin, senlinyan@163.com

文章全文 : translate this paragraph

参考文献

[1]	王顺天, 吴正茂, 吴加贵, 周立, 夏光琼 2015 64 154205 Google Scholar Wang S T, Wu Z M, Wu J G, Zhou L, Xia G Q 2015 Acta Phys. Sin. 64 154205 Google Scholar
[2]	钟东洲, 邓涛, 郑国梁 2014 63 070504 Google Scholar Zhong D Z, Deng T, Zheng G L 2014 Acta Phys. Sin. 63 070504 Google Scholar
[3]	李增, 冯玉玲, 王晓茜, 姚治海 2018 67 140501 Google Scholar Li Z, Feng Y L, Wang X Q, Yao Z H 2018 Acta Phys. Sin. 67 140501 Google Scholar
[4]	张浩, 郭星星, 项水英 2018 67 204202 Google Scholar Zhang H, Guo X X, Xiang S Y 2018 Acta Phys. Sin. 67 204202 Google Scholar
[5]	穆鹏华, 潘炜, 李念强, 闫连山, 罗斌, 邹喜华, 徐明峰 2015 64 124206 Google Scholar Mu P H, Pan W, Li N Q, Yan L S, Luo B, Zou X H, Xu M F 2015 Acta Phys. Sin. 64 124206 Google Scholar
[6]	Sciamanna, Shore K A 2015 Nat. Photon. 9 151 Google Scholar
[7]	Jiang N, Xue C, Liu D, Lv Y, Qiu K 2017 Opt. Lett. 42 1055 Google Scholar
[8]	Yi L, Ke J, Xia G, Hu W 2018 J. Opt. 20 024004 Google Scholar
[9]	Ning J, Anke Z, Shiqin L, Chenpeng X, Kun Q 2018 Opt. Express 26 32404 Google Scholar
[10]	Qiliang L, Dewang C, Qi B, Ran Z, Miao H 2019 Appl. Opt. 58 1715 Google Scholar
[11]	Fu Y, Cheng M, Jiang X, Deng L, Ke C, Fu S, ang M, Zhang M, Shum P, Liu D 2018 Nonlin. Dyn. 94 1949 Google Scholar
[12]	Ott E, Grebogi C, Yorke J A 1990 Phys. Rev. Lett. 64 1196 Google Scholar
[13]	张旭东, 朱萍, 谢小平, 何国光 2013 62 210506 Google Scholar Zhang X D, Zhu P, Xie X P, He G G 2013 Acta Phys. Sin. 62 210506 Google Scholar
[14]	谭文, 王耀南, 刘祖润, 周少武 2002 51 2463 Google Scholar Tan W, Wang Y N, Liu Z R, Zhou S W 2002 Acta Phys. Sin. 51 2463 Google Scholar
[15]	关新平, 范正平, 彭海朋, 王益群 2001 50 2108 Google Scholar Guan X P, Fan Z P, Peng H P, Wang Y Q 2001 Acta Phys. Sin. 50 2108 Google Scholar
[16]	Levy G, Hardy A 1998 IEEE J. Quant. Eletron. 34 1 Google Scholar
[17]	Labate A, Ciofini M, Meucci R 1998 Phys. Rev. E 57 5230 Google Scholar
[18]	Yan S L 2009 Chin. Sci. Bull. 54 1158 Google Scholar
[19]	Yan S L 2009 J. Mod. Opt. 56 539 Google Scholar
[20]	Yan S L 2016 Chin. Phys. B 25 090504 Google Scholar
[21]	颜森林 2015 64 240505 Google Scholar Yan S L 2015 Acta Phys. Sin. 64 240505 Google Scholar
[22]	Wang A B, Yang Y B, Wang B J, Zhang B B, Li L, Wang Y C 2013 Opt. Express 21 8701 Google Scholar
[23]	Xiang S, Pan W, Zhang L, Wen A, Shang L, Zhang, Lin L 2014 Opt. Commun. 324 38 Google Scholar
[24]	姬玉林, 郭晓敏, 李璞, 刘香莲, 张建国, 郭龑强 2018 中国激光 45 1008001 Google Scholar Ji Y L, Guo X M, Li P, Liu X L, Zhang J G, Guo Y Q 2018 Chinese Journal of Lasers 45 1008001 Google Scholar
[25]	张胜海, 杨华, 钱兴中 2004 53 3706 Google Scholar Zhang S H, Yang H, Qian X Z 2004 Acta Phys. Sin. 53 3706 Google Scholar
[26]	吕翎, 商锦玉, 朱佳博, 沈娜, 柳爽, 张新 2012 61 140504 Google Scholar Lü L, Shang J Y, Zhu J B, Shen N, Liu S, Zhang X 2012 Acta Phys. Sin. 61 140504 Google Scholar
[27]	李春来, 杨本珊, 黄乐, 冯婷, 何瑶, 邹卯荣 2015 64 030504 Google Scholar Li C L, Yang B S, Huang L Feng T, He Y, Zou M R 2015 Acta Phys. Sin. 64 030504 Google Scholar
[28]	祝金川, 李成仁, 齐笳羽, 任旭东, 岳喜爽 2011 60 104213 Google Scholar Zhu J C, Li C R, Qi J Y, Ren X D, Yue S X 2011 Acta Phys. Sin. 60 104213 Google Scholar
[29]	范文华, 田小建, 于永力, 陈菊芳, 罗红娥 2005 55 5105 Google Scholar Fan W H, Tian X J, Yu Y L, Chen J F, Luo H E 2005 Acta Phys. Sin. 55 5105 Google Scholar
[30]	秦洁, 于洪洁 2007 56 6828 Google Scholar Qin J, YU H J 2007 Acta Phys. Sin. 56 6828 Google Scholar
[31]	孙娟, 李晓霞, 张金浩, 申玉卓, 李艳雨 2017 66 188901 Google Scholar Sun J, Li X X, Zhang J H, Shen Y Z, Li Y Y 2017 Acta Phys. Sin. 66 188901 Google Scholar
[32]	李春来, 禹思敏, 罗晓曙 2012 61 110502 Google Scholar Li C L, Yu S M, Luo X S 2012 Acta Phys. Sin. 61 110502 Google Scholar
[33]	孔江涛, 黄健, 龚建兴, 李尔玉 2018 67 098901 Google Scholar Kong J T, Huang J, Gong J X, Li E Y 2018 Acta Phys. Sin. 67 098901 Google Scholar
[34]	梁义, 王兴元 2013 62 018901 Google Scholar Liang Y, Wang X Y 2013 Acta Phys. Sin. 62 018901 Google Scholar
[35]	Yin C Y, Wang B H, Wang W X, Chen G R 2008 Phys. Rev. E 77 027102 Google Scholar
[36]	Liu W, Shi P 2019 Automatica 101 345 Google Scholar
[37]	Mulet J, Mirasso C, Heil T, Fischer I 2004 J. Opt. B: Quantum Semiclass. Opt. 6 97 Google Scholar
[38]	Hill M T, De Waardt H, Dorren H J S 2001 IEEE J. Quantum Electron. 37 405 Google Scholar
[39]	Zhang W L, Pan W, Luo B, Li X F, Zou X H, Wang M Y 2007 J. Opt. Soc. Am. B 24 1276 Google Scholar
[40]	Hong Y H 2015 IEEE J. Select. Topics Quantum Electron. 21 1801007 Google Scholar
[41]	颜森林 2019 68 170502 Google Scholar Yan S L 2019 Acta Phys. Sin. 68 170502 Google Scholar

施引文献

图 1 激光局域控制网络图, ⊕表示光电转换控制器

Fig. 1. A controlled laser local area network. Signal ⊕ is the photoelectric controller.

下载: 全尺寸图片幻灯片

图 2 激光器t1与r1链路混沌同步

Fig. 2. Chaotic laser t1 synchronizes with the laser r1.

下载: 全尺寸图片幻灯片

图 3 激光器t2与r2链路混沌同步

Fig. 3. Chaotic laser t2 synchronizes with the laser r2.

下载: 全尺寸图片幻灯片

图 4 激光器t1与r1取得9周期同步

Fig. 4. The laser t1 synchronizes with the laser r1 at a 9-periodic state.

下载: 全尺寸图片幻灯片

图 5 激光器t2与r2取得6周期同步

Fig. 5. The laser t2 synchronizes with the laser r2 at a 6-periodic state.

下载: 全尺寸图片幻灯片

图 6 激光器t1与r1取得2周期同步

Fig. 6. The laser t1 synchronizes with the laser r1 at a 2-periodic state.

下载: 全尺寸图片幻灯片

图 7 激光器t2与r2取得2周期同步

Fig. 7. The laser t2 synchronizes with the laser r2 at another 2-periodic state.

下载: 全尺寸图片幻灯片

图 8 激光器t1与r1取得4周期同步

Fig. 8. The laser t1 synchronizes with the laser r1 at a 4-periodic state.

下载: 全尺寸图片幻灯片

图 9 激光器t2与r2取得4周期同步

Fig. 9. The laser t2 synchronizes with the laser r2 at another 4-periodic state.

下载: 全尺寸图片幻灯片

图 10 激光器t1与r1取得6周期同步

Fig. 10. The laser t1 synchronizes with the laser r1 at a 6-periodic state.

下载: 全尺寸图片幻灯片

图 11 激光器t2与r2取得5周期同步

Fig. 11. The laser t2 synchronizes with the laser r2 at a 5-periodic state.

下载: 全尺寸图片幻灯片

图 12 激光器t1与r1取得类周期动态同步

Fig. 12. The laser t1 synchronizes dynamically with the laser r1 in quasi-periodicity.

下载: 全尺寸图片幻灯片

图 13 激光器t2与r2取得类周期动态同步

Fig. 13. The laser t2 synchronizes dynamically with the laser r2 in quasi-periodicity.

下载: 全尺寸图片幻灯片

图 14 激光器t1超宽带通信

Fig. 14. The laser t1 performs an ultra-wideband communication.

下载: 全尺寸图片幻灯片

图 15 激光器r1又一个超宽带通信

Fig. 15. The laser r1 performs another ultra-wideband communication.

下载: 全尺寸图片幻灯片

图 16 激光器t1与r1取得混沌同步发射

Fig. 16. The lasers t1 and r1 emit synchronously two same chaotic carriers.

下载: 全尺寸图片幻灯片

表 1 激光器参量

Table 1. Laser parameters.

参量	值	参量	值
腔长 L/μm	350	俄歇复合因子C/(cm⁶·s^–1)	3.5 × 10^–29
腔宽 w/μm	2	饱和光子场振幅\|E_s\|/m^–3/2	1.6619 × 10¹¹
腔厚 d/μm	0.15	增益常数 α/cm²	2.3 × 10^–16
压缩和限制因子Γ	0.29	光线宽增强因子 β_c	6
群速度折射率n_g	3.8	耦合驱动系数 k	0.055
光子损耗系数 α_m/ cm^–1	49	频率差 Δω/(Rad·s^–1)	2π × 10^–9
非辐射复合速率 A_nr/s^–1	1.0 × 10⁸	激光透明时载流子密度 n_th/cm^–3	1.2 × 10¹⁸
辐射复合因子 B/(cm³·s^–1)	1.2 × 10^–10	光在腔内来回一周的时间 τ_L/s	8.8667 × 10^–12
驱动电流 I_{t1, t2}/ mA	34, 30	光反馈系数 k_r	0.15

下载: 导出CSV

map

[1]	王顺天, 吴正茂, 吴加贵, 周立, 夏光琼 2015 64 154205 Google Scholar Wang S T, Wu Z M, Wu J G, Zhou L, Xia G Q 2015 Acta Phys. Sin. 64 154205 Google Scholar
[2]	钟东洲, 邓涛, 郑国梁 2014 63 070504 Google Scholar Zhong D Z, Deng T, Zheng G L 2014 Acta Phys. Sin. 63 070504 Google Scholar
[3]	李增, 冯玉玲, 王晓茜, 姚治海 2018 67 140501 Google Scholar Li Z, Feng Y L, Wang X Q, Yao Z H 2018 Acta Phys. Sin. 67 140501 Google Scholar
[4]	张浩, 郭星星, 项水英 2018 67 204202 Google Scholar Zhang H, Guo X X, Xiang S Y 2018 Acta Phys. Sin. 67 204202 Google Scholar
[5]	穆鹏华, 潘炜, 李念强, 闫连山, 罗斌, 邹喜华, 徐明峰 2015 64 124206 Google Scholar Mu P H, Pan W, Li N Q, Yan L S, Luo B, Zou X H, Xu M F 2015 Acta Phys. Sin. 64 124206 Google Scholar
[6]	Sciamanna, Shore K A 2015 Nat. Photon. 9 151 Google Scholar
[7]	Jiang N, Xue C, Liu D, Lv Y, Qiu K 2017 Opt. Lett. 42 1055 Google Scholar
[8]	Yi L, Ke J, Xia G, Hu W 2018 J. Opt. 20 024004 Google Scholar
[9]	Ning J, Anke Z, Shiqin L, Chenpeng X, Kun Q 2018 Opt. Express 26 32404 Google Scholar
[10]	Qiliang L, Dewang C, Qi B, Ran Z, Miao H 2019 Appl. Opt. 58 1715 Google Scholar
[11]	Fu Y, Cheng M, Jiang X, Deng L, Ke C, Fu S, ang M, Zhang M, Shum P, Liu D 2018 Nonlin. Dyn. 94 1949 Google Scholar
[12]	Ott E, Grebogi C, Yorke J A 1990 Phys. Rev. Lett. 64 1196 Google Scholar
[13]	张旭东, 朱萍, 谢小平, 何国光 2013 62 210506 Google Scholar Zhang X D, Zhu P, Xie X P, He G G 2013 Acta Phys. Sin. 62 210506 Google Scholar
[14]	谭文, 王耀南, 刘祖润, 周少武 2002 51 2463 Google Scholar Tan W, Wang Y N, Liu Z R, Zhou S W 2002 Acta Phys. Sin. 51 2463 Google Scholar
[15]	关新平, 范正平, 彭海朋, 王益群 2001 50 2108 Google Scholar Guan X P, Fan Z P, Peng H P, Wang Y Q 2001 Acta Phys. Sin. 50 2108 Google Scholar
[16]	Levy G, Hardy A 1998 IEEE J. Quant. Eletron. 34 1 Google Scholar
[17]	Labate A, Ciofini M, Meucci R 1998 Phys. Rev. E 57 5230 Google Scholar
[18]	Yan S L 2009 Chin. Sci. Bull. 54 1158 Google Scholar
[19]	Yan S L 2009 J. Mod. Opt. 56 539 Google Scholar
[20]	Yan S L 2016 Chin. Phys. B 25 090504 Google Scholar
[21]	颜森林 2015 64 240505 Google Scholar Yan S L 2015 Acta Phys. Sin. 64 240505 Google Scholar
[22]	Wang A B, Yang Y B, Wang B J, Zhang B B, Li L, Wang Y C 2013 Opt. Express 21 8701 Google Scholar
[23]	Xiang S, Pan W, Zhang L, Wen A, Shang L, Zhang, Lin L 2014 Opt. Commun. 324 38 Google Scholar
[24]	姬玉林, 郭晓敏, 李璞, 刘香莲, 张建国, 郭龑强 2018 中国激光 45 1008001 Google Scholar Ji Y L, Guo X M, Li P, Liu X L, Zhang J G, Guo Y Q 2018 Chinese Journal of Lasers 45 1008001 Google Scholar
[25]	张胜海, 杨华, 钱兴中 2004 53 3706 Google Scholar Zhang S H, Yang H, Qian X Z 2004 Acta Phys. Sin. 53 3706 Google Scholar
[26]	吕翎, 商锦玉, 朱佳博, 沈娜, 柳爽, 张新 2012 61 140504 Google Scholar Lü L, Shang J Y, Zhu J B, Shen N, Liu S, Zhang X 2012 Acta Phys. Sin. 61 140504 Google Scholar
[27]	李春来, 杨本珊, 黄乐, 冯婷, 何瑶, 邹卯荣 2015 64 030504 Google Scholar Li C L, Yang B S, Huang L Feng T, He Y, Zou M R 2015 Acta Phys. Sin. 64 030504 Google Scholar
[28]	祝金川, 李成仁, 齐笳羽, 任旭东, 岳喜爽 2011 60 104213 Google Scholar Zhu J C, Li C R, Qi J Y, Ren X D, Yue S X 2011 Acta Phys. Sin. 60 104213 Google Scholar
[29]	范文华, 田小建, 于永力, 陈菊芳, 罗红娥 2005 55 5105 Google Scholar Fan W H, Tian X J, Yu Y L, Chen J F, Luo H E 2005 Acta Phys. Sin. 55 5105 Google Scholar
[30]	秦洁, 于洪洁 2007 56 6828 Google Scholar Qin J, YU H J 2007 Acta Phys. Sin. 56 6828 Google Scholar
[31]	孙娟, 李晓霞, 张金浩, 申玉卓, 李艳雨 2017 66 188901 Google Scholar Sun J, Li X X, Zhang J H, Shen Y Z, Li Y Y 2017 Acta Phys. Sin. 66 188901 Google Scholar
[32]	李春来, 禹思敏, 罗晓曙 2012 61 110502 Google Scholar Li C L, Yu S M, Luo X S 2012 Acta Phys. Sin. 61 110502 Google Scholar
[33]	孔江涛, 黄健, 龚建兴, 李尔玉 2018 67 098901 Google Scholar Kong J T, Huang J, Gong J X, Li E Y 2018 Acta Phys. Sin. 67 098901 Google Scholar
[34]	梁义, 王兴元 2013 62 018901 Google Scholar Liang Y, Wang X Y 2013 Acta Phys. Sin. 62 018901 Google Scholar
[35]	Yin C Y, Wang B H, Wang W X, Chen G R 2008 Phys. Rev. E 77 027102 Google Scholar
[36]	Liu W, Shi P 2019 Automatica 101 345 Google Scholar
[37]	Mulet J, Mirasso C, Heil T, Fischer I 2004 J. Opt. B: Quantum Semiclass. Opt. 6 97 Google Scholar
[38]	Hill M T, De Waardt H, Dorren H J S 2001 IEEE J. Quantum Electron. 37 405 Google Scholar
[39]	Zhang W L, Pan W, Luo B, Li X F, Zou X H, Wang M Y 2007 J. Opt. Soc. Am. B 24 1276 Google Scholar
[40]	Hong Y H 2015 IEEE J. Select. Topics Quantum Electron. 21 1801007 Google Scholar
[41]	颜森林 2019 68 170502 Google Scholar Yan S L 2019 Acta Phys. Sin. 68 170502 Google Scholar

[1]	颜森林. 激光混沌并行串联同步及其在中继器保密通信系统中的应用. , 2019, 68(17): 170502. doi: 10.7498/aps.68.20190212
[2]	颜森林. 半导体激光器混沌法拉第效应控制方法. , 2015, 64(24): 240505. doi: 10.7498/aps.64.240505
[3]	李雨珊, 吕翎, 刘烨, 刘硕, 闫兵兵, 常欢, 周佳楠. 复杂网络时空混沌同步的Backstepping设计. , 2013, 62(2): 020513. doi: 10.7498/aps.62.020513
[4]	颜森林. 激光混沌并联同步及其在全光逻辑门中的应用研究. , 2013, 62(23): 230504. doi: 10.7498/aps.62.230504
[5]	郑艳斌, 宋煜, 杜宝祥, 潘晶, 丁群. 一种混沌密码序列周期特性检测新方法. , 2012, 61(23): 230501. doi: 10.7498/aps.61.230501
[6]	颜森林. 外部光注入空间耦合半导体激光器高维混沌系统的增频与控制研究. , 2012, 61(16): 160505. doi: 10.7498/aps.61.160505
[7]	吕翎, 李钢, 商锦玉, 沈娜, 张新, 柳爽, 朱佳博. 最近邻耦合网络的时空混沌同步研究. , 2010, 59(9): 5966-5971. doi: 10.7498/aps.59.5966
[8]	吕翎, 邹家蕊, 杨明, 孟乐, 郭丽, 柴元. 大规模富社团网络的时空混沌同步. , 2010, 59(10): 6864-6870. doi: 10.7498/aps.59.6864
[9]	敬晓丹, 吕翎. 非线性耦合完全网络的时空混沌同步. , 2009, 58(11): 7539-7543. doi: 10.7498/aps.58.7539
[10]	颜森林. 外腔延时反馈半导体激光器混沌偏振可调控制方法研究. , 2008, 57(11): 6878-6882. doi: 10.7498/aps.57.6878
[11]	颜森林. 半导体激光器混沌光电延时负反馈控制方法研究. , 2008, 57(4): 2100-2106. doi: 10.7498/aps.57.2100
[12]	颜森林. 延时反馈半导体激光器双劈控制混沌方法研究. , 2008, 57(5): 2827-2831. doi: 10.7498/aps.57.2827
[13]	罗润梓. 一个新混沌系统的脉冲控制与同步. , 2007, 56(10): 5655-5660. doi: 10.7498/aps.56.5655
[14]	王占山, 张化光, 王智良. 一类混沌神经网络的全局同步. , 2006, 55(6): 2687-2693. doi: 10.7498/aps.55.2687
[15]	颜森林, 汪胜前. 激光混沌串联同步以及混沌中继器系统理论研究. , 2006, 55(4): 1687-1695. doi: 10.7498/aps.55.1687
[16]	颜森林. 注入半导体激光器混沌相位周期控制方法研究. , 2006, 55(10): 5109-5114. doi: 10.7498/aps.55.5109
[17]	颜森林. 量子阱激光器混沌相位控制同步以及编码研究. , 2005, 54(3): 1098-1104. doi: 10.7498/aps.54.1098
[18]	颜森林, 迟泽英, 陈文建, 王泽农. 激光混沌同步和解码以及优化. , 2004, 53(6): 1704-1709. doi: 10.7498/aps.53.1704
[19]	尹逊和, 任勇, 山秀明. 广义Hénon映射的滑模变结构控制同步. , 2002, 51(9): 1949-1953. doi: 10.7498/aps.51.1949
[20]	高金峰, 马西奎, 罗先觉. 实现连续时间标量混沌信号同步的自适应控制方法. , 2000, 49(7): 1235-1240. doi: 10.7498/aps.49.1235

计量

文章访问数: 4848
PDF下载量: 61
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

激光局域网络的混沌控制及并行队列同步