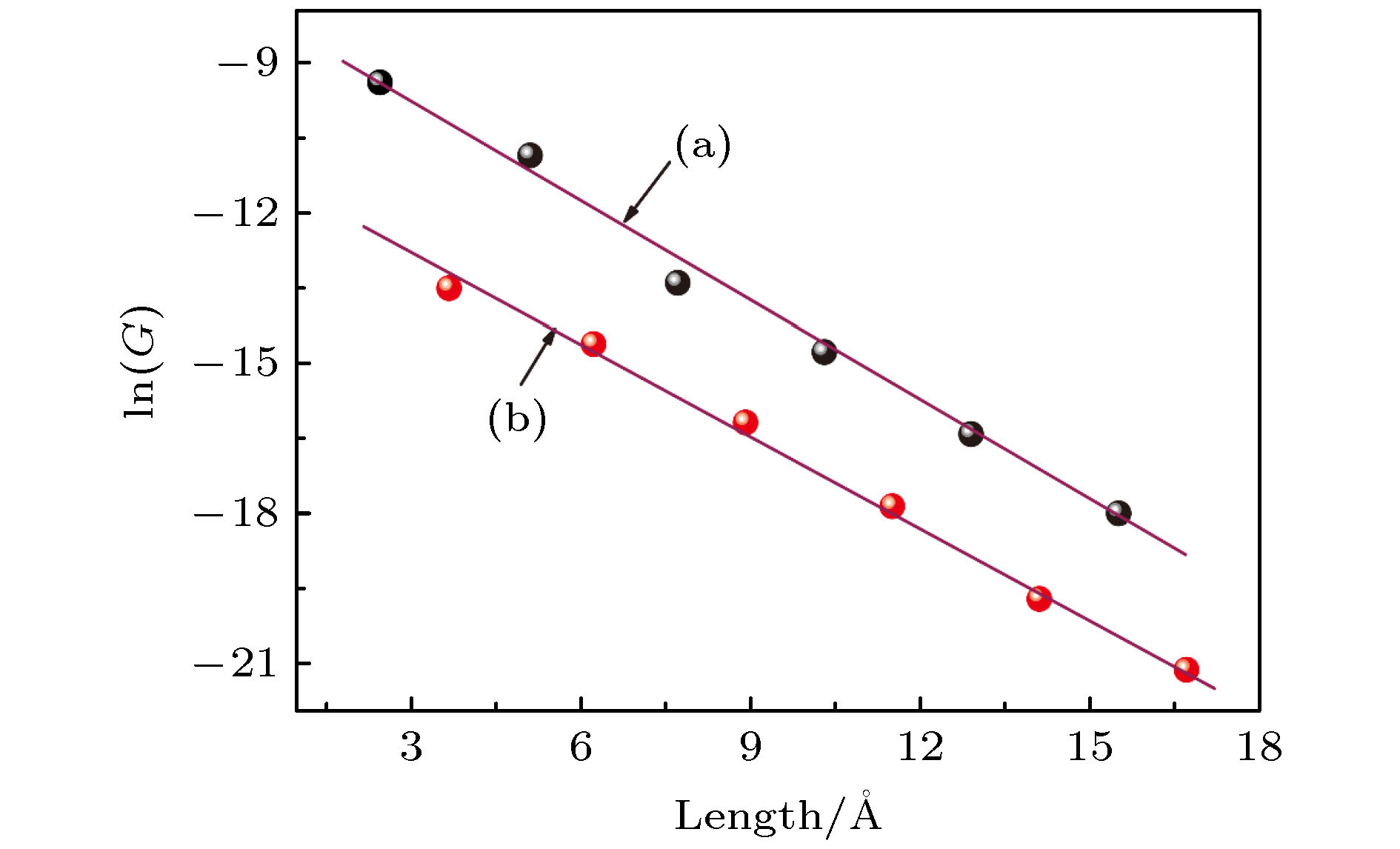
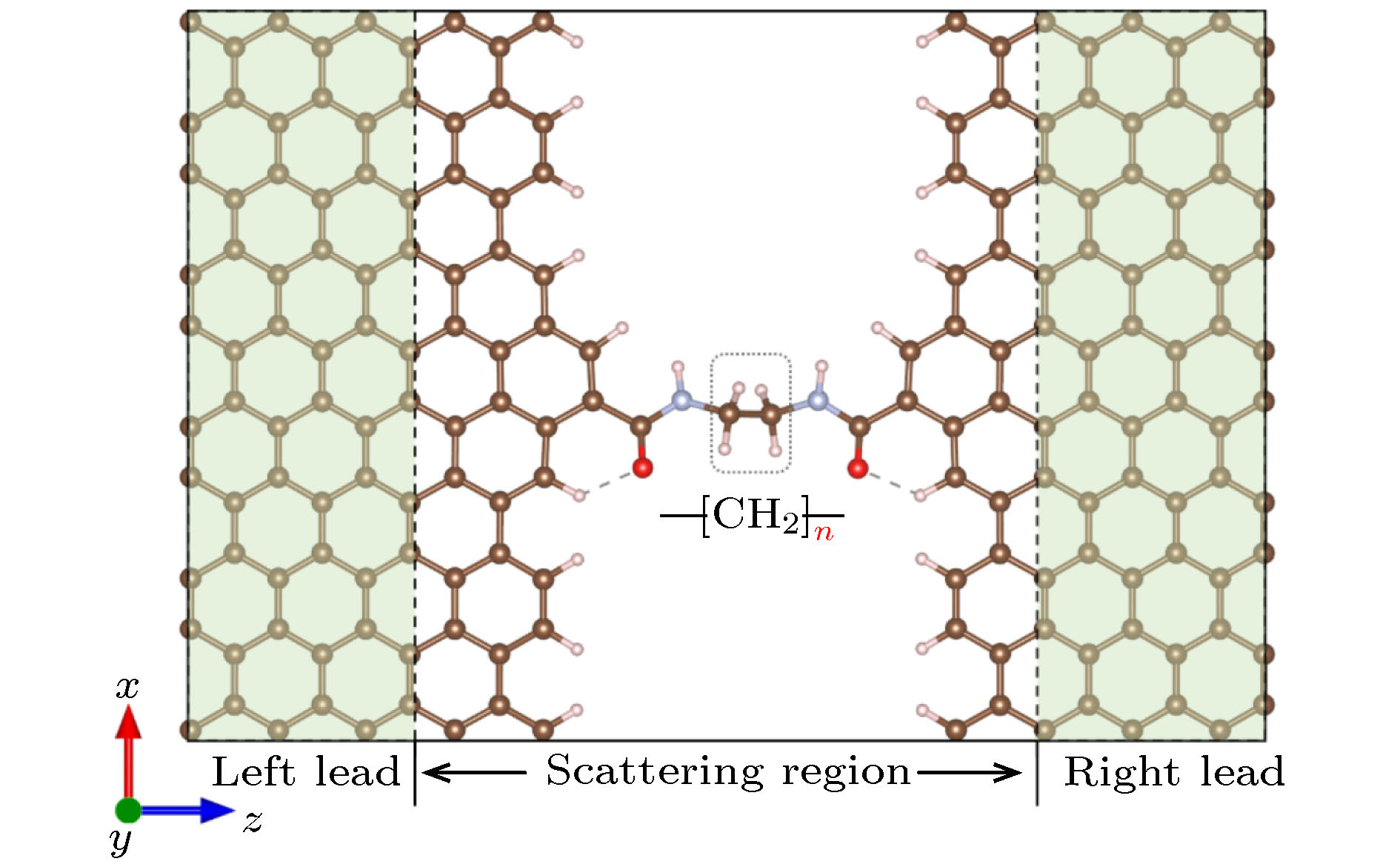
-
一维非共轭烷烃链虽不具富电子或少电子特征, 但常存在于单分子器件或多肽、蛋白质等生物分子中, 对电子传输产生重要影响. 为理解这类物质的电子输运特征, 本研究设计了一维线性非共轭(CH2)n分子结模型, 并利用密度泛函理论结合非平衡态格林函数的方法, 对(CH2)n(n = 1—12)线性分子链与两个石墨烯电极耦合而成的分子结进行了第一性原理计算. 结果表明, CH2分子链随着n值的变化, 其电导值表现出明显的奇偶振荡现象, 并且随着链长的增加呈指数级的衰减, 这一结果与实验研究取得了很好的一致性, 为理解和设计性能更加优良的单分子器件提供了重要理论依据.Although the one-dimensional non-conjugated alkane chain, which has an important influence on the electron transport process, does not possess the characteristics of electron-rich and electron-deficient, it often exists in single-molecule devices and biological molecules such as peptides and proteins. In order to understand the electron transport characteristics of alkane chain, a one-dimensional linear non-conjugate (CH2)n molecular junction model is designed in this study. Subsequently, we conduct the systematic study of the electronic transport behavior of (CH2)n (n = 1–12) molecular linear chain coupling to two graphene electrodes, based on the density functional theory and nonequilibrium Green’s function formalism. The results reveal that the structure and conductance of CH2 chain are highly sensitive to the odevity of CH2 unit. When the value of n is odd, the groups of CH2 extend in a zigzag way from the left electrode to the right electrode in the plane of graphene, while the value of n is even, what is different is that the groups of CH2 are arranged above and below the electrode plane. For this reason, the odd-even behavior of conductance occurs in the (CH2)n (n = 1–12) molecular chain. Furthermore, n is also an important factor to affect their transport properties (odd or even behavior of conductance). The longer the (CH2)n chain, the deeper the suppression in transmission spectrum and the lower the equilibrium conductance. What is more, the conductance decreases exponentially with the increase of molecular length, with a decay constant β of 0.67 and 0.60 for odd and even, respectively, which is in good agreement with the experimental research. Additionally, by analyzing their eigenchannels of odd and even (CH2)n molecular chain, we find that the coplanar σ electron with graphene electrode makes a major contribution to the electronic transport channel. The current-voltage curve of (CH2)n molecular chain exhibits nonlinearity, implying their semiconductor characteristics. The interesting mechanical and electronic transport properties are expected to conduce to further experimental synthesis, design and operation of the single molecular nanodevices.
-
Keywords:
- methylene /
- first-principles calculation /
- electron transport /
- non-equilibrium Green’s function
[1] Xin N, Guan J, Zhou C, Chen X, Gu C, Li Y, Ratner M A, Nitzan A, Stoddart J F, Guo X 2019 Nat. Rev. Phy. 1 211
Google Scholar
[2] Wen B, Cao M, Lu M, Cao W, Shi H, Liu J, Wang X, Jin H, Fang X, Wang W, Yuan J 2014 Adv. Mater. 26 3484
Google Scholar
[3] Cao M-S, Wang X X, Zhang M, Cao W Q, Fang X Y, Yuan J 2020 Adv. Mater. 32 1907156
Google Scholar
[4] Balci O, Polat E O, Kakenov N, Kocabas C 2015 Nat. Commun. 6 6628
Google Scholar
[5] Meng L, Xin N, Hu C, Wang J, Gui B, Shi J, Wang C, Shen C, Zhang G, Guo H, Meng S, Guo X 2019 Nat. Commun. 10 1450
Google Scholar
[6] Li Y, Zhao L, Yao Y, Guo X 2019 ACS Appl Bio Mater 3 68
Google Scholar
[7] Zhou C, Li X, Gong Z, Jia C, Lin Y, Gu C, He G, Zhong Y, Yang J, Guo X 2018 Nat. Commun. 9 807
Google Scholar
[8] Li Y, Yang C, Guo X 2020 Acc. Chem. Res. 53 159
Google Scholar
[9] Jia C, Migliore A, Xin N, Huang S, Wang J, Yang Q, Wang S, Chen H, Wang D, Feng B, Liu Z, Zhang G, Qu D H, Tian H, Ratner M A, Xu H Q, Nitzan A, Guo X 2016 Science 352 1443
Google Scholar
[10] Zotti L A, Cuevas J C 2018 ACS Omega 3 3778
Google Scholar
[11] Guo C, Yu X, Refaely-Abramson S, Sepunaru L, Bendikov T, Pecht I, Kronik L, Vilan A, Sheves M, Cahen D 2016 Proc. Natl. Acad. Sci. U. S. A. 113 10785
Google Scholar
[12] Schosser W M, Zotti L A, Cuevas J C, Pauly F 2019 J. Chem. Phys. 150 174705
Google Scholar
[13] Mu Y, Zhou Y, Zhang T, Zeng Z-Y, Cheng Y 2017 J. Chem. Eng. Data 62 3889
Google Scholar
[14] Liu F T, Cheng Y, Yang F-B, Chen X R 2014 Physica E 56 96
Google Scholar
[15] 贺园园, 程娜, 赵健伟 2017 化学学报 75 893
Google Scholar
He Y Y, Cheng N, Zhao J W 2017 Acta Chim. Sin. 75 893
Google Scholar
[16] 左敏, 廖文虎, 吴丹, 林丽娥 2019 68 237302
Google Scholar
Zuo M, Liao W H, Wu D, Lin L E 2019 Acta Phys. Sin. 68 237302
Google Scholar
[17] 刘南舒, 周思, 赵纪军 2019 物理化学学报 35 1142
Google Scholar
Liu N S, Zhou S, Zhao J J 2019 Acta Phys.Chem. Sin. 35 1142
Google Scholar
[18] Fang X Y, Yu X X, Zheng H M, Jin H B, Wang L, Cao M-S 2015 Phys. Lett. A 379 2245
Google Scholar
[19] Malen J A, Doak P, Baheti K, Tilley T D, Segalman R A, Majumdar A 2009 Nano Lett. 9 1164
Google Scholar
[20] Soler J M, Artacho E, Gale J D, García A, Junquera J, Ordejón P, Sánchez-Portal D 2002 J. Phys.: Condens. Matter 14 2745
Google Scholar
[21] Artacho E, Anglada E, Diéguez O, Gale J D, García A, Junquera J, Martin R M, Ordejón P, Pruneda J M, Sánchez-Portal D, Soler J M 2008 J. Phys.: Condens. Matter 20 064208
Google Scholar
[22] García A, Papior N, Akhtar A, Artacho E, Blum V, Bosoni E, Brandimarte P, Brandbyge M, Cerdá J I, Corsetti F, Cuadrado R, Dikan V, Ferrer J, Gale J, García-Fernández P, García-Suárez V M, García S, Huhs G, Illera S, Korytár R, Koval P, Lebedeva I, Lin L, López-Tarifa P, Mayo S G, Mohr S, Ordejón P, Postnikov A, Pouillon Y, Pruneda M, Robles R, Sánchez-Portal D, Soler J M, Ullah R, Yu V W-z, Junquera J 2020 J. Chem. Phys. 152 204108
Google Scholar
[23] Perdew J P, Burke K, Ernzerhof M 1996 Phys. Rev. Lett. 77 3865
Google Scholar
[24] Troullier N, Martins J L 1991 Phys. Rev. B 43 1993
Google Scholar
[25] Brandbyge M, Mozos J L, Ordejón P, Taylor J, Stokbro K 2002 Phys. Rev. B 65 165401
Google Scholar
[26] Frederiksen T, Paulsson M, Brandbyge M, Jauho A P 2007 Phys. Rev. B 75 205413
Google Scholar
[27] Momma K, Izumi F 2011 J. Appl. Crystallogr. 44 1272
Google Scholar
[28] Lang N D, Avouris P 1998 Phys. Rev. Lett. 81 3515
Google Scholar
[29] Li Y J, Li S L, Gong P, Li Y L, Fang X Y, Jia Y H, Cao M-S 2018 Physica E 104 247
Google Scholar
[30] 陈熙, 张胜利 2018 物理化学学报 34 1061
Google Scholar
Chen X, Zhang S L 2018 Acta Phys.Chem. Sin. 34 1061
Google Scholar
[31] 柳福提, 张淑华, 程艳, 陈向荣, 程晓洪 2016 65 106201
Google Scholar
Liu F T, Zhang S H, Cheng Y, Chen X R, Cheng X H 2016 Acta Phys. Sin. 65 106201
Google Scholar
-
图 1 (CH2)n分子结(n = 1−12)计算模型示意图(金色球: 碳原子C, 红色球: 氧原子O, 灰色球: 氮原子N, 淡粉色球: 氢原子H)
Fig. 1. Schematic illustration of (CH2)n (n = 1−12) molecule junction (golden ball: carbon atom, red ball, oxygen atom, grey ball: nitrogen atom, light pink ball: hydrogen atom).
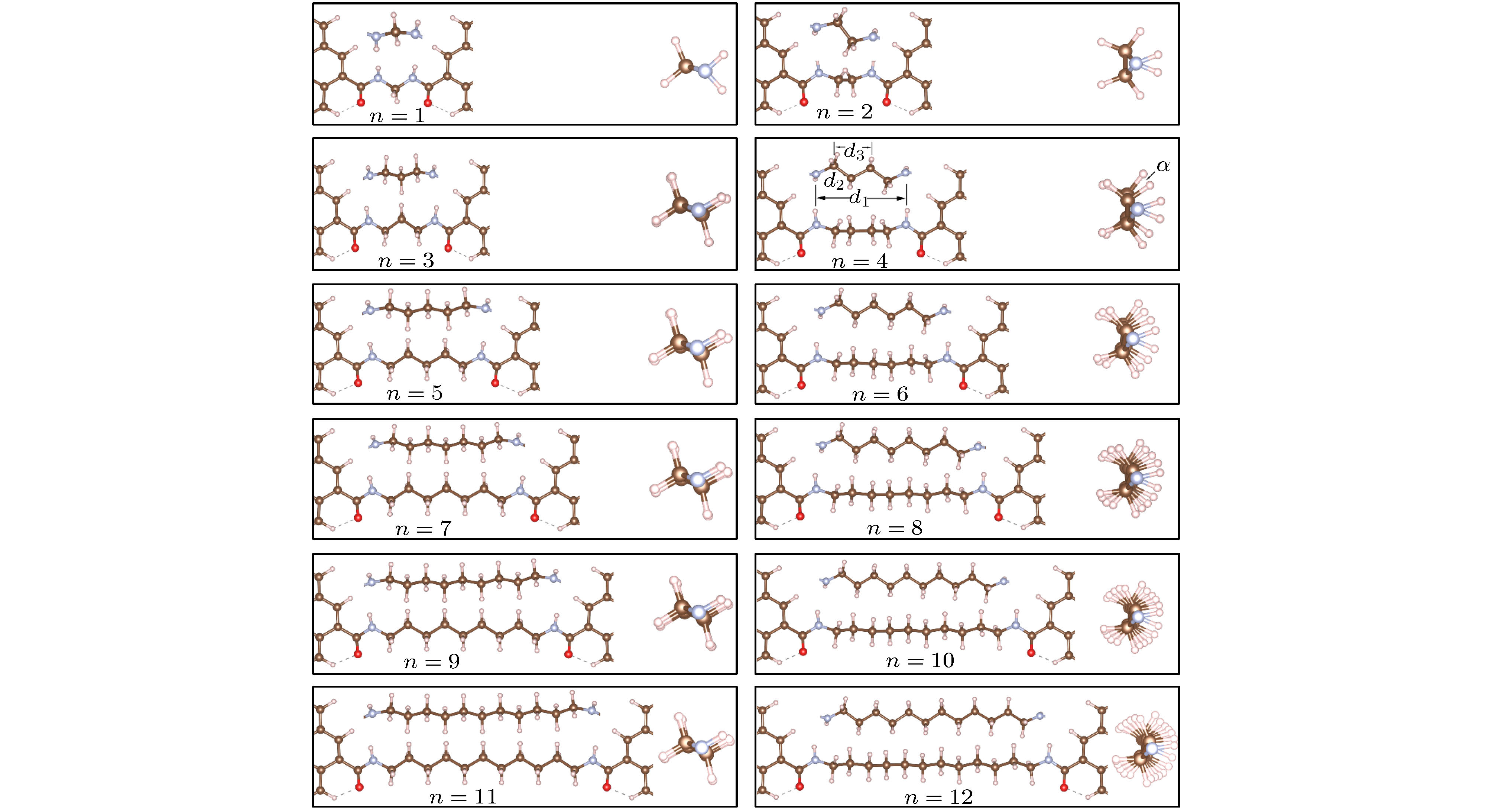
图 2 (CH2)n分子结(n = 1−12)稳定结构图(每个图中下方为沿y轴方向的俯视图, 上方和右方插图分别为沿x和z轴方向的侧视图, 坐标方向和小球颜色说明见图1)
Fig. 2. The stable structure of (CH2)n (n = 1−12) molecule junction (on each diagram, the bottom figure is a top view along y axis, the upper and right side inset is a side view along x and z axis, respectively. Coordinate direction and color description of the ball are shown in Fig. 1).
图 3 奇数 (a)和偶数(b) (CH2)n分子结在零偏压下的透射谱图
Fig. 3. Transmission coefficient as a function of energy for odd (a) and even (b) (CH2)n molecule junction under zero external bias.
图 4 奇数 (a)和偶数(b) (CH2)n分子结零偏压电导与分子链长度关系图
Fig. 4. The plot of conductance versus chain length for odd (a) and even (b) molecular junction of (CH2)n at the bias of 0 V.
图 5 奇数 (a)和偶数(b) (CH2)n分子结导电通道图(上方插图为沿x轴的侧视图, 蓝色和黄色区域分别代表得失电荷密度)
Fig. 5. The eigenchannels of odd (a) and even (b) molecular junction of (CH2)n (The upper inset is a side view along x axis, blue and yellow areas denote the gain and loss of electron density)
图 6 奇数 (a)和偶数(b) (CH2)n分子结在不同电压下的电流图
Fig. 6. The current of odd (a) and even (b) (CH2)n molecular junction under different external bias.
表 1 (CH2)n分子结(n = 1—12)的平均键长、键角和结合能(d1, d2, d3, α如图2所示)
Table 1. The average bond length, bond angle and binding energy in (CH2)n (n = 1–12) molecule junction (the bond length of d1, d2, d3 and the bond angle α are shown in Fig. 2).
n d1N—N /Å d2C—C /Å d3C—C /Å α/(°) ΔE/eV 1 2.44 — — — –10.90 2 3.67 1.55 — — –11.04 3 5.10 1.55 2.54 2.25 –11.12 4 6.22 1.53 2.55 18.81 –11.45 5 7.71 1.55 2.63 0.91 –11.52 6 8.91 1.54 2.59 15.12 –11.55 7 10.30 1.55 2.62 0.41 –11.66 8 11.51 1.54 2.60 14.61 –11.57 9 12.90 1.55 2.62 0.80 –11.69 10 14.11 1.54 2.61 14.93 –11.60 11 15.51 1.55 2.62 1.85 –11.72 12 16.71 1.54 2.61 14.19 –11.60 
下载: 导出CSV
-
[1] Xin N, Guan J, Zhou C, Chen X, Gu C, Li Y, Ratner M A, Nitzan A, Stoddart J F, Guo X 2019 Nat. Rev. Phy. 1 211
Google Scholar
[2] Wen B, Cao M, Lu M, Cao W, Shi H, Liu J, Wang X, Jin H, Fang X, Wang W, Yuan J 2014 Adv. Mater. 26 3484
Google Scholar
[3] Cao M-S, Wang X X, Zhang M, Cao W Q, Fang X Y, Yuan J 2020 Adv. Mater. 32 1907156
Google Scholar
[4] Balci O, Polat E O, Kakenov N, Kocabas C 2015 Nat. Commun. 6 6628
Google Scholar
[5] Meng L, Xin N, Hu C, Wang J, Gui B, Shi J, Wang C, Shen C, Zhang G, Guo H, Meng S, Guo X 2019 Nat. Commun. 10 1450
Google Scholar
[6] Li Y, Zhao L, Yao Y, Guo X 2019 ACS Appl Bio Mater 3 68
Google Scholar
[7] Zhou C, Li X, Gong Z, Jia C, Lin Y, Gu C, He G, Zhong Y, Yang J, Guo X 2018 Nat. Commun. 9 807
Google Scholar
[8] Li Y, Yang C, Guo X 2020 Acc. Chem. Res. 53 159
Google Scholar
[9] Jia C, Migliore A, Xin N, Huang S, Wang J, Yang Q, Wang S, Chen H, Wang D, Feng B, Liu Z, Zhang G, Qu D H, Tian H, Ratner M A, Xu H Q, Nitzan A, Guo X 2016 Science 352 1443
Google Scholar
[10] Zotti L A, Cuevas J C 2018 ACS Omega 3 3778
Google Scholar
[11] Guo C, Yu X, Refaely-Abramson S, Sepunaru L, Bendikov T, Pecht I, Kronik L, Vilan A, Sheves M, Cahen D 2016 Proc. Natl. Acad. Sci. U. S. A. 113 10785
Google Scholar
[12] Schosser W M, Zotti L A, Cuevas J C, Pauly F 2019 J. Chem. Phys. 150 174705
Google Scholar
[13] Mu Y, Zhou Y, Zhang T, Zeng Z-Y, Cheng Y 2017 J. Chem. Eng. Data 62 3889
Google Scholar
[14] Liu F T, Cheng Y, Yang F-B, Chen X R 2014 Physica E 56 96
Google Scholar
[15] 贺园园, 程娜, 赵健伟 2017 化学学报 75 893
Google Scholar
He Y Y, Cheng N, Zhao J W 2017 Acta Chim. Sin. 75 893
Google Scholar
[16] 左敏, 廖文虎, 吴丹, 林丽娥 2019 68 237302
Google Scholar
Zuo M, Liao W H, Wu D, Lin L E 2019 Acta Phys. Sin. 68 237302
Google Scholar
[17] 刘南舒, 周思, 赵纪军 2019 物理化学学报 35 1142
Google Scholar
Liu N S, Zhou S, Zhao J J 2019 Acta Phys.Chem. Sin. 35 1142
Google Scholar
[18] Fang X Y, Yu X X, Zheng H M, Jin H B, Wang L, Cao M-S 2015 Phys. Lett. A 379 2245
Google Scholar
[19] Malen J A, Doak P, Baheti K, Tilley T D, Segalman R A, Majumdar A 2009 Nano Lett. 9 1164
Google Scholar
[20] Soler J M, Artacho E, Gale J D, García A, Junquera J, Ordejón P, Sánchez-Portal D 2002 J. Phys.: Condens. Matter 14 2745
Google Scholar
[21] Artacho E, Anglada E, Diéguez O, Gale J D, García A, Junquera J, Martin R M, Ordejón P, Pruneda J M, Sánchez-Portal D, Soler J M 2008 J. Phys.: Condens. Matter 20 064208
Google Scholar
[22] García A, Papior N, Akhtar A, Artacho E, Blum V, Bosoni E, Brandimarte P, Brandbyge M, Cerdá J I, Corsetti F, Cuadrado R, Dikan V, Ferrer J, Gale J, García-Fernández P, García-Suárez V M, García S, Huhs G, Illera S, Korytár R, Koval P, Lebedeva I, Lin L, López-Tarifa P, Mayo S G, Mohr S, Ordejón P, Postnikov A, Pouillon Y, Pruneda M, Robles R, Sánchez-Portal D, Soler J M, Ullah R, Yu V W-z, Junquera J 2020 J. Chem. Phys. 152 204108
Google Scholar
[23] Perdew J P, Burke K, Ernzerhof M 1996 Phys. Rev. Lett. 77 3865
Google Scholar
[24] Troullier N, Martins J L 1991 Phys. Rev. B 43 1993
Google Scholar
[25] Brandbyge M, Mozos J L, Ordejón P, Taylor J, Stokbro K 2002 Phys. Rev. B 65 165401
Google Scholar
[26] Frederiksen T, Paulsson M, Brandbyge M, Jauho A P 2007 Phys. Rev. B 75 205413
Google Scholar
[27] Momma K, Izumi F 2011 J. Appl. Crystallogr. 44 1272
Google Scholar
[28] Lang N D, Avouris P 1998 Phys. Rev. Lett. 81 3515
Google Scholar
[29] Li Y J, Li S L, Gong P, Li Y L, Fang X Y, Jia Y H, Cao M-S 2018 Physica E 104 247
Google Scholar
[30] 陈熙, 张胜利 2018 物理化学学报 34 1061
Google Scholar
Chen X, Zhang S L 2018 Acta Phys.Chem. Sin. 34 1061
Google Scholar
[31] 柳福提, 张淑华, 程艳, 陈向荣, 程晓洪 2016 65 106201
Google Scholar
Liu F T, Zhang S H, Cheng Y, Chen X R, Cheng X H 2016 Acta Phys. Sin. 65 106201
Google Scholar
下载:
计量
- 文章访问数: 5110
- PDF下载量: 80
- 被引次数: 0
