-
量子密钥分发融合经典通信方案将连续变量量子密钥分发和经典通信合并到了一起, 为将来在现有的光网络上同时进行密钥分发和经典通信提供了一个有效的方法. 然而, 在量子信号上叠加一个经典信号将会给连续变量量子密钥分发系统引入过噪声从而大大降低系统的性能. 本文提出基于光前置放大器的量子密钥分发融合经典通信方案, 即在接收端插入光前置放大器来提升系统的性能. 首先, 在相同比特误码率条件下, 光前置放大器对信号的放大能够降低对发送端经典信号调制振幅的要求, 从而降低经典信号对量子信号的噪声影响; 其次, 光前置放大器能够补偿接收端探测器的不完美; 再次, 对于本地本振光的情形, 放大器还能放大弱相位参考脉冲, 从而降低参考脉冲散粒噪声带来的相位过噪声. 在实际可达到的系统参数下, 数值仿真结果表明本文提出的方案相比于原方案在安全密钥率和传输距离上都有很好的提升. 这些结果表明本方案为量子密钥分发融合经典通信方案的进一步发展和实际应用提供了一个十分有效而实用的方法.
-
关键词:
- 连续变量 /
- 量子密钥分发融合经典通信 /
- 光前置放大器
That the simultaneous quantum key distribution and classical communication (SQCC) scheme are combined with the continuous variable quantum key distribution (CVQKD) and the classical communication together, will provide an effective method to implement the simultaneous CVQKD and the classical communication in the existing optical networks in the future. However, superimposing a classical signal on the quantum signal will introduce excess noise into the CVQKD system, thus greatly reducing the performance of the system. In this paper, a novel scheme of SQCC based on optical preamplifier (OPA) is proposed, that is, the OPA is inserted into the receiver to improve the performance of the system. On the one hand, under the condition of the same bit error rate, the amplification of the signal by the OPA can reduce the requirement for the modulation amplitude of the classical signal at the sending end, thereby reducing the noise effect of the classical signal on the quantum signal. On the other hand, the OPA can compensate for the imperfection of the receiver detector. Moreover, in the case of locally generated local oscillator, the amplifier can also amplify the weak phase reference pulse, and thus reducing the phase excess noise caused by the shot noise of the weak phase reference pulse. Numerical simulation results show that the proposed scheme has better performance than the original scheme in the sense of security key rate and transmission distance. These results show that this scheme provides an effective and practical method for the further development and practical application of the SQCC scheme.-
Keywords:
- continuous variable /
- simultaneous quantum key distribution and classical communication /
- optical preamplifier
[1] 李剑, 陈彦桦, 潘泽世, 孙风琪, 李娜, 黎蕾蕾 2016 3 030302
Google Scholar
Li J, Chen Y H, Pan Z S, Sun F Q, Li N, Li L L 2016 Acta Phys. Sin. 3 030302
Google Scholar
[2] 苗二龙, 莫小范, 桂有珍, 韩正甫, 郭光灿 2004 53 2123
Google Scholar
Miao E L, Mo X F, Gui Y Z, Han Z F, Guo G C 2004 Acta Phys. Sin. 53 2123
Google Scholar
[3] 曹正文, 张爽浩, 冯晓毅, 赵光, 柴庚, 李东伟 2017 66 020301
Google Scholar
Cao Z W, Zhang S H, Peng X Y, Zhao G, Chai G, Li D W 2017 Acta Phys. Sin. 66 020301
Google Scholar
[4] Lo H K, Curty M, Tamaki K 2014 Nat. Photonics 8 595
Google Scholar
[5] Braunstein S L, van Loock P 2005 Rev. Mod. Phys. 77 513
Google Scholar
[6] Pirandola S, Andersen U L, Banchi L, Berta M, Bunandar D, Colbeck R, Englund D, Gehring T, Lupo C, Ottaviani C, Pereira J L, Razavi M, Shaari J S, Tomamichel M, Usenko V C, Vallone G, Villoresi P, Wallden P 2020 Adv. Opt. Photon. 12 1012
[7] Bennett C H, Brassard G 1984 Proceedings of IEEE International Conference on Computers Systems, and Signal Processing Bangalore, India, December 10–12, 1984 p175
[8] Grosshans F, Grangier P 2002 Phys. Rev. Lett. 88 057902
Google Scholar
[9] Leverrier A, Grosshans F, Grangier P 2010 Phys. Rev. A 81 062343
Google Scholar
[10] Leverrier A 2015 Phys. Rev. Lett. 114 070501
Google Scholar
[11] Qi B, Lougovski P, Pooser R, Grice W, Bobrek M 2015 Phys. Rev. X 5 041009
Google Scholar
[12] Huang D, Huang P, Lin D K, Wang C, Zeng G H 2015 Opt. Lett. 40 3695
Google Scholar
[13] Huang D, Huang P, Lin D, Zeng G 2016 Sci. Rep. 6 19201
Google Scholar
[14] Huang D, Lin D K, Wang C, Liu W Q, Fang S H, Peng J Y, Huang P, Zeng G H 2015 Opt. Express 23 17511
Google Scholar
[15] Zhang Y C, Chen Z Y, Pirandola S, Wang X Y, Zhou C, Chu B J, Zhao Y J, Xu B J, Yu S, Guo H 2020 Phys. Rev. Lett. 125 010502
Google Scholar
[16] Fossier S, Diamanti E, Debuisschert T, Villing A, Tuallebrouri R, Grangier P 2009 New J. Phys. 11 045023
Google Scholar
[17] Huang D, Huang P, Li H, Wang T, Zhou Y, Zeng G 2016 Opt. Lett. 41 3511
Google Scholar
[18] Qi B, Zhu W, Qian L, Lo H K 2010 New J. Phys. 12 103042
Google Scholar
[19] Kumar R, Qin H, Alleaume R 2015 New J. Phys. 17 043027
Google Scholar
[20] Eriksson T A, Puttnam B J, Rademacher G, Luís R S, Fujiwara M, Takeoka M, Awaji Y, Sasaki M, Wada N 2019 IEEE Photonics Technol. Lett. 31 467
Google Scholar
[21] Qi B 2016 Phys. Rev. A 94 042340
Google Scholar
[22] Qi B, Lim C C W 2018 Phys. Rev. Appl. 9 054008
Google Scholar
[23] Yang C, Ma C, Hu L, He G 2018 Int. J. Theor. Phys. 57 2775
Google Scholar
[24] Wu X, Wang Y, Liao Q, Zhong H, Guo Y 2019 Entropy 21 333
Google Scholar
[25] Wu X D, Wang Y J, Huang D, Guo Y 2020 Front. Phys. 15 31601
Google Scholar
[26] Pan D, Ng S X, Ruan D, Yin L, Long G, Hanzo L 2020 Phys. Rev. A 101 012343
Google Scholar
[27] Guo Y, Liao Q, Wang Y, Huang D, Huang P, Zeng G 2017 Phys. Rev. A 95 032304
Google Scholar
[28] Zhong H, Wang Y J, Wang X D, Liao Q, Wu X D, Guo Y 2018 Entropy 20 578
Google Scholar
[29] Wu X D, Wang Y J, Zhong H, Liao Q, Guo Y 2019 Front. Phys. 14 41501
Google Scholar
[30] Guo Y, Ye W, Zhong H, Liao Q 2019 Phys. Rev. A 99 032327
Google Scholar
[31] Ye W, Zhong H, Liao Q, Huang D, Hu L, Guo Y 2019 Opt. Express 27 17186
Google Scholar
[32] 叶炜, 郭迎, 夏莹, 钟海, 张欢, 丁建枝, 胡利云 2020 69 060301
Google Scholar
Ye W, Guo Y, Xia Y, Zhong H, Zhang H, Ding J Z, Hu L Y 2020 Acta Phys. Sin. 69 060301
Google Scholar
[33] Fossier S, Diamanti E, Debuisschert T, Tualle-Brouri R, Grangier P 2009 J. Phys. B: At. Mol. Opt. Phys. 42 114014
Google Scholar
[34] Lodewyck J, Bloch M, García-Patrón R, Fossier S, Karpov E, Diamanti E, Debuisschert T, Cerf N J, Tualle-Brouri R, McLaughlin S W, Grangier P 2007 Phys. Rev. A 76 042305
Google Scholar
-
图 1 基于前置光放大器的SQCC方案示意图. GM, 高斯调制; VOA, 可调光衰减器; SMF, 单模光纤; PC, 偏振控制器; OPA, 光前置放大器; Hom, 零差探测; Het, 外差探测
Fig. 1. Schematic of the OPA-based SQCC scheme. GM, Gaussian modulation; VOA, variable optical attenuator; SMF, single-mode fiber; PC, polarization controller; OPA, optical preamplifier; Hom, homodyne detection; Het, heterodyne detection.
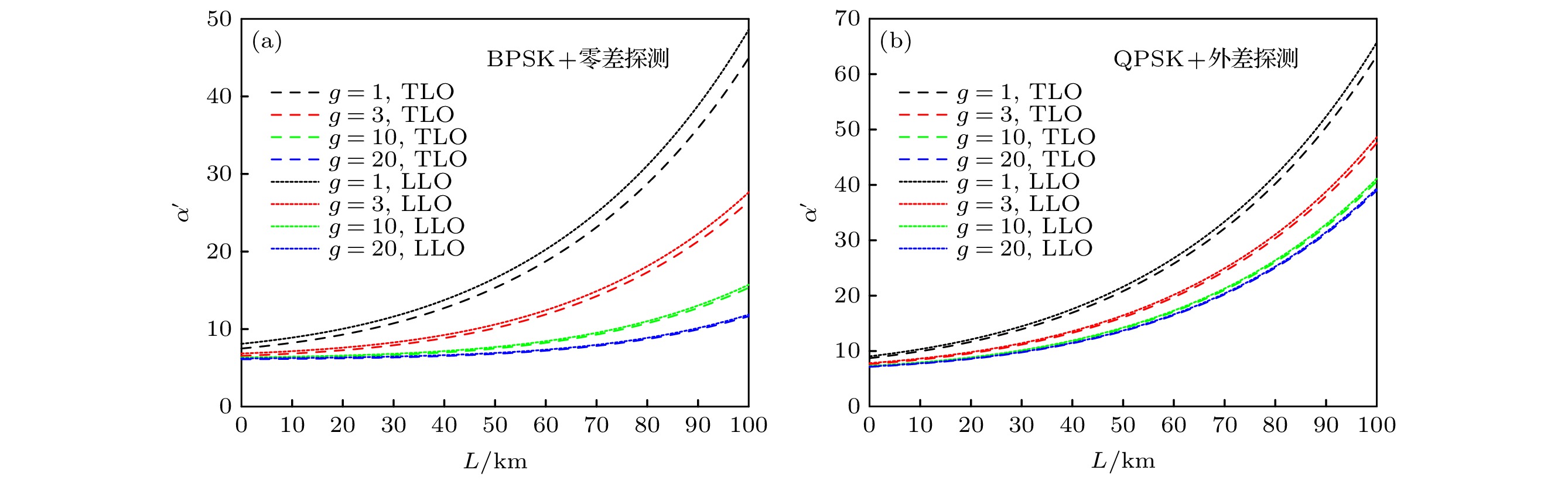
图 2 BER达到
$10^{-9}$ 所需要的相空间位移$\alpha$ 与距离的函数关系 (a) 基于PSA的零差探测情况下的结果; (b) 基于PIA的外差探测情况下的结果. 仿真参数设定如下:$V_{\rm A}= 4$ ,$\gamma$ = 0.2 dB/km,$\eta$ = 0.5,$\xi_{\rm {ele}} = 0.1$ ,$\Delta t = 10^{-9}$ s,$\tau_{\rm c} = 1$ µs,$\xi_0 = 0.01$ ,$N = 1.5$ ; 对于TLO方案,$\eta_{\rm A} = 65$ dB,$\eta_{\rm P} = 35$ dB,$n_{\rm {ref}}^{\rm B} = 10^6$ ,$\sigma_{\varphi} = 10^{-4}$ rad2; 对于LLO方案,$\eta_{\rm A} = 30$ dB,$\eta_{\rm P} = 30$ dB,$n_{\rm {ref}}^{\rm B} = 10^3$ ,$\sigma_{\rm I} = 10^{-4}$ rad2,$\sigma_{{\rm B}_0} = 2\times10^{-3}$ rad2Fig. 2. The needed phase space displacement
$\alpha'$ as a function of transmission distance while BER =$10^{-9}$ : (a) The results under the case of homodyne detection based on PSA; (b) the results under the case of heterodyne detection based on PIA. Simulation parameters are set as follows:$V_{\rm A}=4$ ,$\gamma$ = 0.2 dB/km,$\eta$ = 0.5,$\xi_{\rm {ele}} = 0.1$ ,$\Delta t = 10^{-9}$ s,$\tau_{\rm c} = 1$ µs,$\xi_0 = 0.01$ ,$N = 1.5$ ; for the scheme of TLO,$\eta_{\rm A} = 65$ dB,$\eta_{\rm P} = 35$ dB,$n_{\rm {ref}}^{\rm B} = 10^6$ ,$\sigma_{\varphi} = 10^{-4}$ rad2; for the scheme of LLO,$\eta_{\rm A} = 30$ dB,$\eta_{\rm P} = 30$ dB,$n_{\rm {ref}}^{\rm B} = 10^3$ ,$\sigma_{\rm I} = 10^{-4}$ rad2,$\sigma_{{\rm B}_0} = 2\times10^{-3}$ rad2.
图 3 基于OPA的SQCC方案安全密钥率与传输距离的关系 (a), (b) 当
$\sigma_{\varphi} = 10^{-4}$ rad2和$\sigma_{\rm I} = 10^{-4}$ rad2时, 基于PSA的零差探测和基于PIA的外差探测情形下的安全密钥率与传输距离的关系; (c), (d) 当$\sigma_{\varphi} = 10^{-5}$ rad2和$\sigma_{\rm I} = 10^{-5}$ rad2时, 与(a)和(b)同样情形下的仿真结果Fig. 3. The secure key rate as a function of transmission distance for the proposed OPA-based SQCC scheme: (a), (b) The secure key rate as a function of transmission distance for the PSA-based case with homodyne detection and the PIA-based case with heterodyne detection, while
$\sigma_{\varphi} = 10^{-4}$ rad2 and$\sigma_{\rm I} = 10^{-4}$ rad2; (c), (d) the simulation results for the same cases with (a) and (b), while$\sigma_{\varphi} = 10^{-5}$ rad2 and$\sigma_{\rm I} = 10^{-5}$ rad2. -
[1] 李剑, 陈彦桦, 潘泽世, 孙风琪, 李娜, 黎蕾蕾 2016 3 030302
Google Scholar
Li J, Chen Y H, Pan Z S, Sun F Q, Li N, Li L L 2016 Acta Phys. Sin. 3 030302
Google Scholar
[2] 苗二龙, 莫小范, 桂有珍, 韩正甫, 郭光灿 2004 53 2123
Google Scholar
Miao E L, Mo X F, Gui Y Z, Han Z F, Guo G C 2004 Acta Phys. Sin. 53 2123
Google Scholar
[3] 曹正文, 张爽浩, 冯晓毅, 赵光, 柴庚, 李东伟 2017 66 020301
Google Scholar
Cao Z W, Zhang S H, Peng X Y, Zhao G, Chai G, Li D W 2017 Acta Phys. Sin. 66 020301
Google Scholar
[4] Lo H K, Curty M, Tamaki K 2014 Nat. Photonics 8 595
Google Scholar
[5] Braunstein S L, van Loock P 2005 Rev. Mod. Phys. 77 513
Google Scholar
[6] Pirandola S, Andersen U L, Banchi L, Berta M, Bunandar D, Colbeck R, Englund D, Gehring T, Lupo C, Ottaviani C, Pereira J L, Razavi M, Shaari J S, Tomamichel M, Usenko V C, Vallone G, Villoresi P, Wallden P 2020 Adv. Opt. Photon. 12 1012
[7] Bennett C H, Brassard G 1984 Proceedings of IEEE International Conference on Computers Systems, and Signal Processing Bangalore, India, December 10–12, 1984 p175
[8] Grosshans F, Grangier P 2002 Phys. Rev. Lett. 88 057902
Google Scholar
[9] Leverrier A, Grosshans F, Grangier P 2010 Phys. Rev. A 81 062343
Google Scholar
[10] Leverrier A 2015 Phys. Rev. Lett. 114 070501
Google Scholar
[11] Qi B, Lougovski P, Pooser R, Grice W, Bobrek M 2015 Phys. Rev. X 5 041009
Google Scholar
[12] Huang D, Huang P, Lin D K, Wang C, Zeng G H 2015 Opt. Lett. 40 3695
Google Scholar
[13] Huang D, Huang P, Lin D, Zeng G 2016 Sci. Rep. 6 19201
Google Scholar
[14] Huang D, Lin D K, Wang C, Liu W Q, Fang S H, Peng J Y, Huang P, Zeng G H 2015 Opt. Express 23 17511
Google Scholar
[15] Zhang Y C, Chen Z Y, Pirandola S, Wang X Y, Zhou C, Chu B J, Zhao Y J, Xu B J, Yu S, Guo H 2020 Phys. Rev. Lett. 125 010502
Google Scholar
[16] Fossier S, Diamanti E, Debuisschert T, Villing A, Tuallebrouri R, Grangier P 2009 New J. Phys. 11 045023
Google Scholar
[17] Huang D, Huang P, Li H, Wang T, Zhou Y, Zeng G 2016 Opt. Lett. 41 3511
Google Scholar
[18] Qi B, Zhu W, Qian L, Lo H K 2010 New J. Phys. 12 103042
Google Scholar
[19] Kumar R, Qin H, Alleaume R 2015 New J. Phys. 17 043027
Google Scholar
[20] Eriksson T A, Puttnam B J, Rademacher G, Luís R S, Fujiwara M, Takeoka M, Awaji Y, Sasaki M, Wada N 2019 IEEE Photonics Technol. Lett. 31 467
Google Scholar
[21] Qi B 2016 Phys. Rev. A 94 042340
Google Scholar
[22] Qi B, Lim C C W 2018 Phys. Rev. Appl. 9 054008
Google Scholar
[23] Yang C, Ma C, Hu L, He G 2018 Int. J. Theor. Phys. 57 2775
Google Scholar
[24] Wu X, Wang Y, Liao Q, Zhong H, Guo Y 2019 Entropy 21 333
Google Scholar
[25] Wu X D, Wang Y J, Huang D, Guo Y 2020 Front. Phys. 15 31601
Google Scholar
[26] Pan D, Ng S X, Ruan D, Yin L, Long G, Hanzo L 2020 Phys. Rev. A 101 012343
Google Scholar
[27] Guo Y, Liao Q, Wang Y, Huang D, Huang P, Zeng G 2017 Phys. Rev. A 95 032304
Google Scholar
[28] Zhong H, Wang Y J, Wang X D, Liao Q, Wu X D, Guo Y 2018 Entropy 20 578
Google Scholar
[29] Wu X D, Wang Y J, Zhong H, Liao Q, Guo Y 2019 Front. Phys. 14 41501
Google Scholar
[30] Guo Y, Ye W, Zhong H, Liao Q 2019 Phys. Rev. A 99 032327
Google Scholar
[31] Ye W, Zhong H, Liao Q, Huang D, Hu L, Guo Y 2019 Opt. Express 27 17186
Google Scholar
[32] 叶炜, 郭迎, 夏莹, 钟海, 张欢, 丁建枝, 胡利云 2020 69 060301
Google Scholar
Ye W, Guo Y, Xia Y, Zhong H, Zhang H, Ding J Z, Hu L Y 2020 Acta Phys. Sin. 69 060301
Google Scholar
[33] Fossier S, Diamanti E, Debuisschert T, Tualle-Brouri R, Grangier P 2009 J. Phys. B: At. Mol. Opt. Phys. 42 114014
Google Scholar
[34] Lodewyck J, Bloch M, García-Patrón R, Fossier S, Karpov E, Diamanti E, Debuisschert T, Cerf N J, Tualle-Brouri R, McLaughlin S W, Grangier P 2007 Phys. Rev. A 76 042305
Google Scholar
下载:
计量
- 文章访问数: 5519
- PDF下载量: 96
- 被引次数: 0
