-
Fokas系统是最简单的二维空间非线性演化模型. 本文首先研究一种相似变换将该系统转换为长波-短波共振模型形式; 然后基于该相似变换和已知的长波-短波共振模型的有理形式解, 通过选择空间变量y的待定函数为Hermite函数, 得到了Fokas系统的一个有理函数表示的严格解析解; 进而选定合适自由参数给出了Fokas系统丰富的二维怪波激发, 并可对二维怪波的形状和幅度进行有效控制; 最后借助图示展现了二维怪波的传播特征. 本文提出的构造Fokas系统二维怪波的途径可以作为一种激发二维怪波现象的潜在物理机制, 并推广应用于其他(2 + 1)维非线性局域或非局域模型.
-
关键词:
- 二维怪波 /
- Fokas系统 /
- (2 + 1)非线性演化模型 /
- 相似变换
Rogue wave (RW) is one of the most fascinating phenomena in nature and has been observed recently in nonlinear optics and water wave tanks. It is considered as a large and spontaneous nonlinear wave and seems to appear from nowhere and disappear without a trace. The Fokas system is the simplest two-dimensional nonlinear evolution model. In this paper, we firstly study a similarity transformation for transforming the system into a long wave-short wave resonance model. Secondly, based on the similarity transformation and the known rational form solution of the long-wave-short-wave resonance model, we give the explicit expressions of the rational function form solutions by means of an undetermined function of the spatial variable y, which is selected as the Hermite function. Finally, we investigate the rich two-dimensional rogue wave excitation and discuss the control of its amplitude and shape, and reveal the propagation characteristics of two-dimensional rogue wave through graphical representation under choosing appropriate free parameter. The results show that the two-dimensional rogue wave structure is controlled by four parameters: ${\rho _0},\;n,\;k,\;{\rm{and}}\;\omega \left( {{\rm{or}}\;\alpha } \right)$ . The parameter$ {\rho _0}$ controls directly the amplitude of the two-dimensional rogue wave, and the larger the value of$ {\rho _0}$ , the greater the amplitude of the amplitude of the two-dimensional rogue wave is. The peak number of the two-dimensional rogue wave in the$(x,\;y)$ and$(y,\;t)$ plane depends on merely the parameter n but not on the parameter k. When$n = 0,\;1,\;2, \cdots$ , only single peak appears in the$(x,\;t)$ plane, but single peak, two peaks to three peaks appear in the$(x,\;y)$ and$(y,\;t)$ plane, respectively, for the two-dimensional rogue wave of Fokas system. We can find that the two-dimensional rogue wave occurs from the zero background in the$(x,\;t)$ plane, but the two-dimensional rogue wave appears from the line solitons in the$(x,\;y)$ plane and$(y,\;t)$ plane.It is worth pointing out that the rogue wave obtained here can be used to describe the possible physical mechanism of rogue wave phenomenon, and may have potential applications in other (2 + 1)-dimensional nonlinear local or nonlocal models. -
Keywords:
- two-dimensional rogue wave /
- Fokas system /
- (2 + 1) nonlinear wave model /
- similarity transformation
[1] Pelinovsky E and Kharf C 2008 Extreme Ocean Waves (Berlin: Springer)
[2] Solli R, Ropers C, Koonath P, Jalali B 2007 Nature 450 1054
Google Scholar
[3] Montina A, Bortolozzo U, Residori S, Arecchi F T 2009 Phys. Rev. Lett. 103 173901
Google Scholar
[4] Wabnitz S 2013 J. Opt. 15 064002
Google Scholar
[5] Moslem W M 2011 Phys. Plasm. 18 032301
Google Scholar
[6] Laveder D, Passot T T, Sulem P, Sánchez Arriaga G 2011 Phys. Lett. A 375 3997
Google Scholar
[7] Bludov Yu V, Konotop V V, Akhmediev N 2009 Phys. Rev. A 80 033610
Google Scholar
[8] Efimov V B, Ganshin A N, Kolmakov G V, Mcclintock P V E, Mezhov Deglin L P 2010 Eur. Phys. J. Special Topics 185 181
Google Scholar
[9] Shats M, Punzmann H, Xia H 2010 Phys. Rev. Lett. 104 104503
Google Scholar
[10] Xia H, Maimbourg T, Punzmann H, Shats M 2012 Phys. Rev. Lett. 109 114502
Google Scholar
[11] Vergeles S, Turitsyn S K 2011 Phys. Rev. A 83 061801
Google Scholar
[12] Stenflo L, Marklund M 2010 J. Plasma Phys. 76 293
Google Scholar
[13] Yan Z Y 2010 Commun. Theor. Phys. 54 947
Google Scholar
[14] Demircan A, Amiranashvili S, Brée C, Mahnke C, Mitschke F, Steinmeyer G 2012 Sci. Rep. 2 850
Google Scholar
[15] Driben R, Babushkin I 2012 Opt. Lett. 37 5157
Google Scholar
[16] Marsal N, Caullet V, Wolfersberger D, Sciamanna M 2014 Opt. Lett. 39 3690
Google Scholar
[17] Residori S, Bortolozzo U, Montina A, Lenzini F, Arecchi F T 2012 Fluctuation Noise Lett. 11 1240014
Google Scholar
[18] Soto Crespo J M, Grelu P, Akhmediev N 2011 Phys. Rev. E 84 016604
Google Scholar
[19] Zamora M. J, Garbin B, Barland S, Giudici M, Rios Leite J R, Masoller C, Tredicce J R 2013 Phys. Rev. A 87 035802
Google Scholar
[20] Lecaplain C, Grelu P, Soto Crespo J M, Akhmediev N 2012 Phys. Rev. Lett. 108 233901
Google Scholar
[21] Buccoliero D, Steffensen H, Ebendorff Heidepriem H, Monro T M, Bang O 2011 Opt. Express 19 17973
Google Scholar
[22] Finot C, Hammani K, Fatome J, Dudley J M, Millot G 2010 IEEE J. Quantum Electron. 46 205
Google Scholar
[23] Hammani K, Finot C 2012 Opt. Fiber Technol. 18 93
Google Scholar
[24] Majus D, Jukna V, Valiulis G, Faccio D, Dubietis A 2011 Phys. Rev. A 83 025802
Google Scholar
[25] Hammani K, Finot C, Millot G 2009 Opt. Lett. 34 1138
Google Scholar
[26] Antikainen A, Erkintalo M, Dudley J M, Genty G 2012 Nonlinearity 25 73
Google Scholar
[27] Akhmediev N, Dudley J M, Solli D R, Turitsyn S K 2013 J. Opt. 15 060201
Google Scholar
[28] Chabchoub A, Hoffmann N P, Akhmediev N 2011 Phys. Rev. Lett. 106 204502
Google Scholar
[29] Bailung H, Sharma S K, Nakamura Y 2011 Phys. Rev. Lett. 107 255005
Google Scholar
[30] Randoux S, Suret P 2012 Opt. Lett. 37 500
Google Scholar
[31] 潘昌昌, Baronio F, 陈世华 2020 69 010504
Google Scholar
Pan C C, Baronio F, Chen S H 2020 Acta Phys. Sin. 69 010504
Google Scholar
[32] 李再东, 郭奇奇 2020 69 017501
Google Scholar
Li Z D and Guo Q Q 2020 Acta Phys. Sin. 69 017501
Google Scholar
[33] 陈智敏, 段文山 2020 69 014701
Google Scholar
Chen Z M, Duan W S 2020 Acta Phys. Sin. 69 014701
Google Scholar
[34] 李淑青, 杨光晔, 李禄 2014 63 104215
Google Scholar
Li S Q, Yang G Y, Li L 2014 Acta Phys. Sin. 63 104215
Google Scholar
[35] 张解放, 戴朝卿 2016 65 050501
Google Scholar
Zhang J F, Dai C Q 2016 Acta Phys. Sin. 65 050501
Google Scholar
[36] 胡文成, 张解放, 赵辟, 楼吉辉 2013 62 024216
Google Scholar
Hu W C, Zhang J F, Zhao B, Lou J H 2013 Acta Phys. Sin. 62 024216
Google Scholar
[37] Fokas A S 1994 Inverse Problems 10 19
Google Scholar
[38] Chen J C, Chen Y 2014 J. Nonlinear Math. Phys. 21 454
Google Scholar
[39] Radha R, Lakshmanan M 1997 Chaos, Solitons and Fractals 8 17
Google Scholar
[40] Villarroel J, Prada J, Estévez P G 2009 Stud. Appl. Math. 122 395
Google Scholar
[41] Estévez P G 1999 J. Math. Phys. 40 1406
Google Scholar
[42] Rao J G, Wang L H, Zhang Y, He J S 2015 Commun. Theor. Phys. 64 605
Google Scholar
[43] Chen T T, Hu P Y, He J S 2019 Commun. Theor. Phys. 71 496
Google Scholar
[44] Rao J G, Mihalacheb D, Cheng Y, He J S 2019 Phys.Lett. A 383 1138
Google Scholar
[45] Yan Z Y 2011 J. Math. Anal. Appl. 380 689
[46] Benney D J 1976 Stud. Appl. Math. 55 93
Google Scholar
[47] Kivshar Yu S 1992 Opt. Lett. 17 1322
Google Scholar
[48] Chowdhury A, Tataronis J A 2008 Phys. Rev. Lett. 100 153905
Google Scholar
[49] Zakharov V E 1972 Sov. Phys. JETP 35 908
Google Scholar
[50] Benney D J 1977 Stud. Appl. Math. 56 81
Google Scholar
[51] Djordjevic V D, Redekopp L G 1977 J. Fluid Mech. 79 703
Google Scholar
[52] Ma Y C, Redekopp L G 1979 Phys. Fluids 22 1872
Google Scholar
[53] Chow K W, Chan H N, Kedziora D J, Grimshaw R H J 2013 J. Phys. Soc. Jpn. 82 074001
Google Scholar
[54] Chen S H, Grelu P, Soto Crespo J M 2014 Phys. Rev. E 89 011201
Google Scholar
[55] Abramowitz M, Stegun I A 1965 Handbook of Mathematical Functions (New York: Dover Publications)
-
图 1
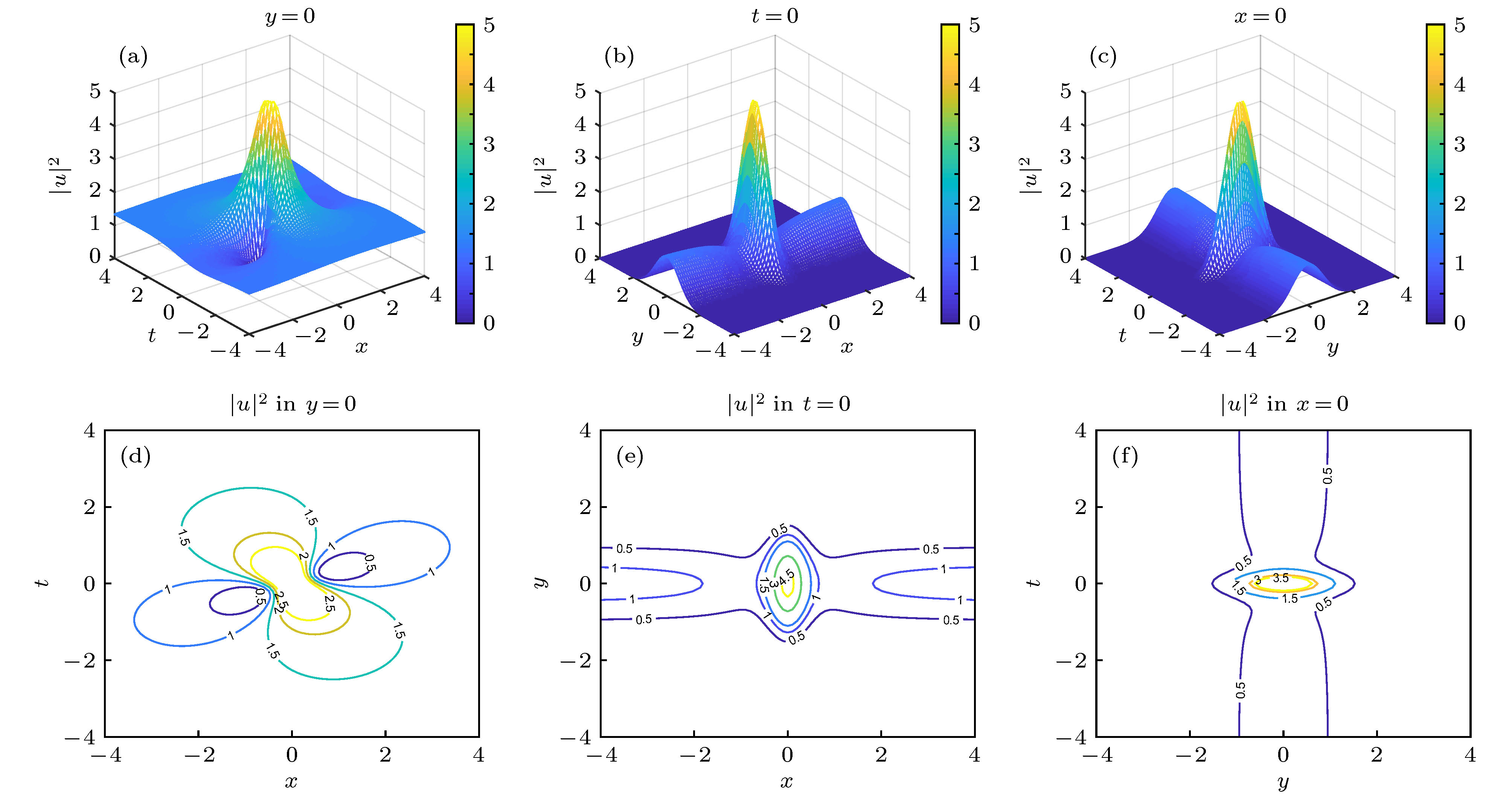
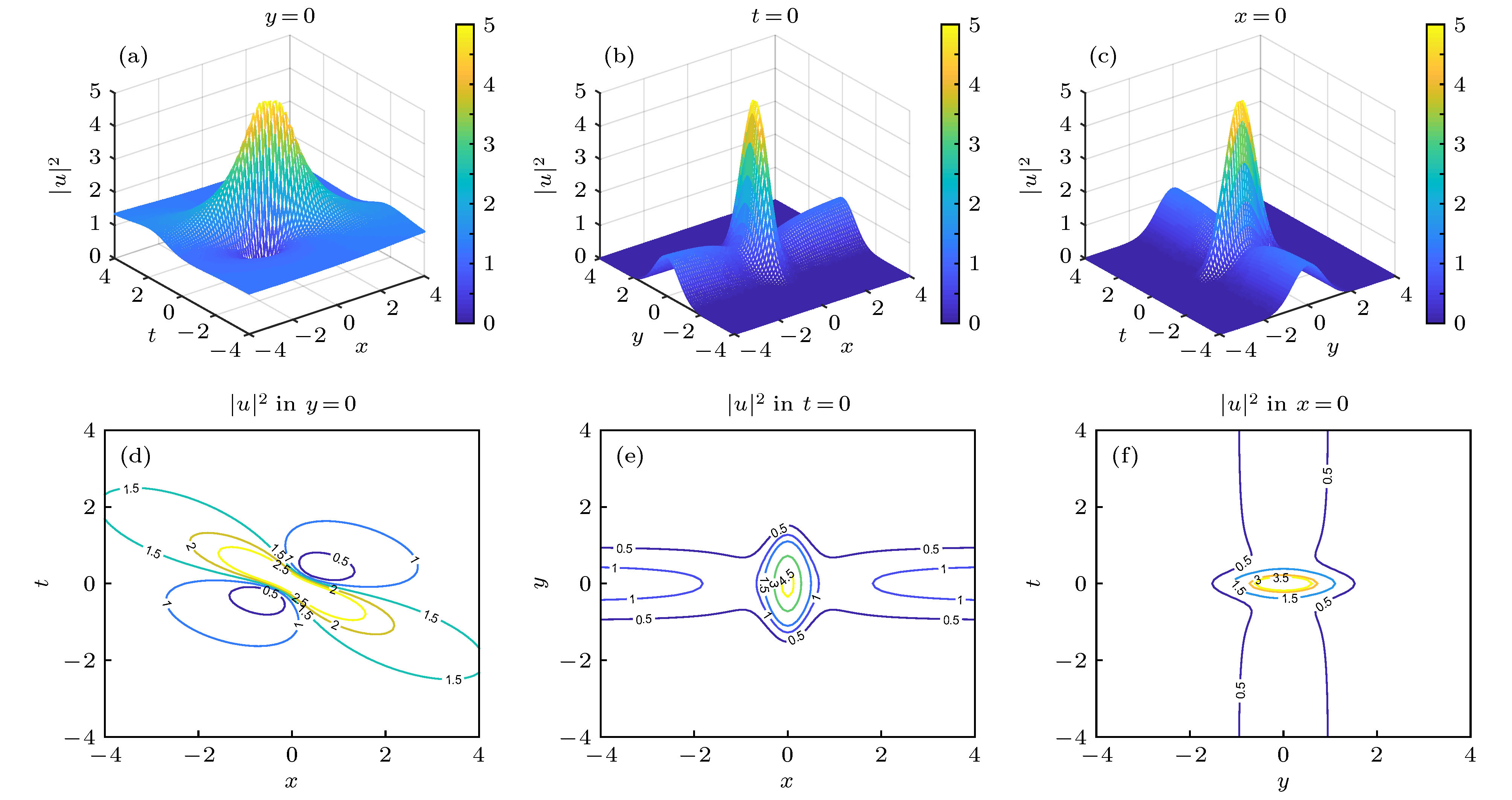
${\rho _0} = 1.5,\; \alpha = {\left| \omega \right|^{ - 1}} = 1,\; n = 0$ ,$k = 0$ 时, 由(22)式所确定的二维怪波激发 (a), (d)$y = 0$ 时在$\left( {x, t} \right)$ 平面上的演化图和相应的等高线图; (b), (e)$t = 0$ 时在$\left( {x, y} \right)$ 平面上的演化图和相应的等高线图; (c), (f)$x = 0$ 时在$\left( {y, t} \right)$ 平面的演化图和相应的等高线图Fig. 1. Cross-sections of two-dimensional rogue wave propagations (top row) and contour plots (bottom row) for the density distribution
${\left| {u\left( {x, y, t} \right)} \right|^2}$ given in Eq. (22) for${\rho _0} = 1.5,\; \alpha =$ ${\left| \omega \right|^{ - 1}} = 1,\; n = 0$ with$k = 0$ : (a), (d)$\left( {x, t} \right)$ -plan with$y = 0$ ; (b), (e)$\left( {x, y} \right)$ -space with$t = 0$ ; (c), (f)$\left( {y, t} \right)$ -plane with$x = 0$ .
图 2
${\rho _0} = 1.5,\; \alpha = {\left| \omega \right|^{ - 1}} = 1,\; n = 0$ ,$k = 1$ 时, 由(22)式所确定的二维怪波激发 (a), (d)$y = 0$ 时在$\left( {x, t} \right)$ 平面上的演化图和相应的等高线图; (b), (e)$t = 0$ 时在$\left( {x, y} \right)$ 平面上的演化图和相应的等高线图; (c), (f)$x = 0$ 时在$\left( {y, t} \right)$ 平面的演化图和相应的等高线图Fig. 2. Cross-sections of two-dimensional rogue wave propagations (top row) and contour plots (bottom row) for the density distribution
${\left| {u\left( {x, y, t} \right)} \right|^2}$ given in Eq. (22) for${\rho _0} = 1.5,\; \alpha = {\left| \omega \right|^{ - 1}} = 1,\; n = 0$ with$k = 1$ : (a), (d)$\left( {x, t} \right)$ -plane with$y = 0$ ; (b), (e)$\left( {x, y} \right)$ -space with$t = 0$ ; (c), (f)$\left( {y, t} \right)$ -plane with$x = 0$ .
图 3
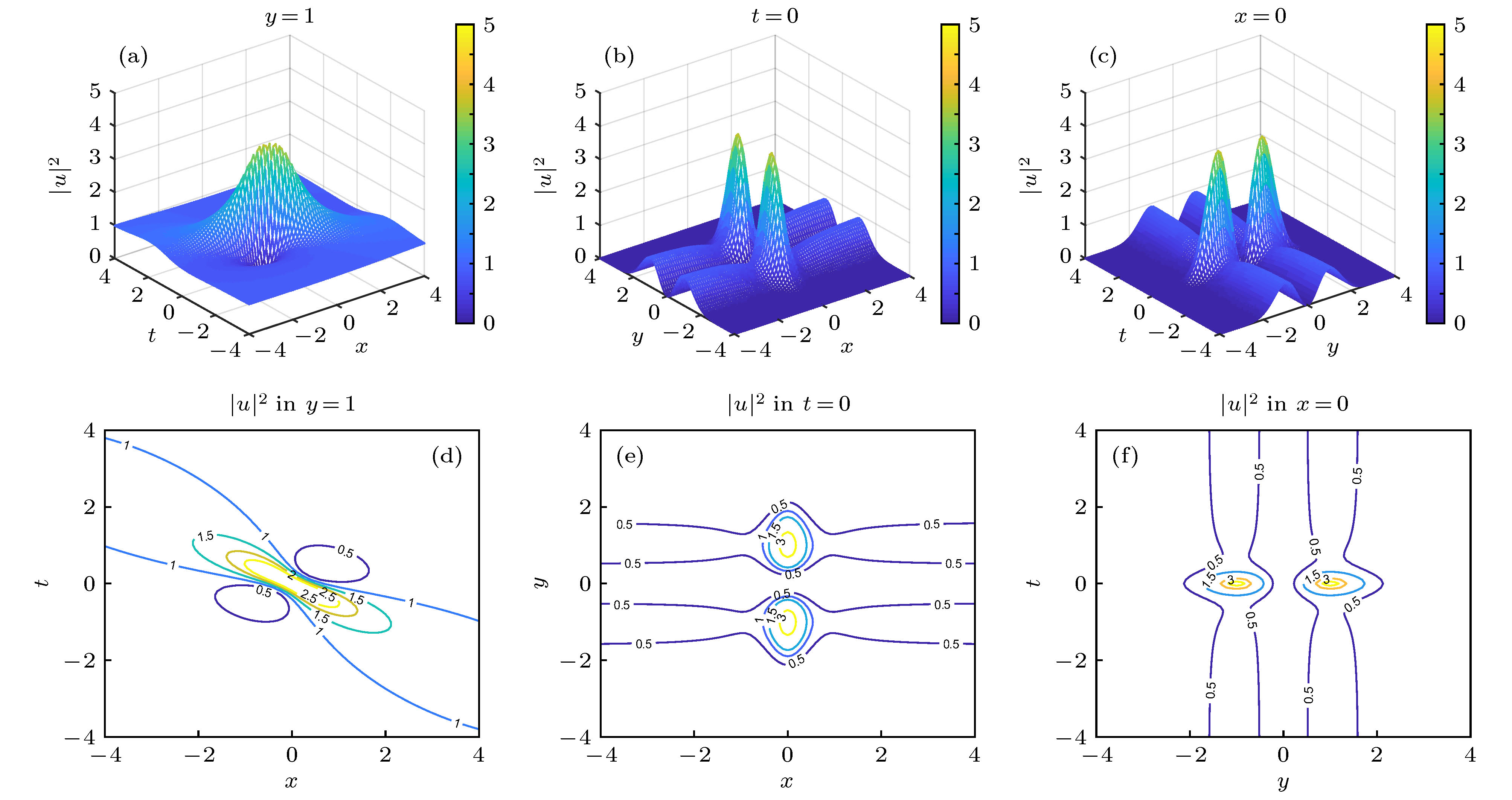
${\rho _0} = 1.5,\; \alpha = {\left| \omega \right|^{ - 1}} = 1,\; n = 1$ ,$k = 0$ 时, 由(22)式所确定的二维怪波激发 (a), (d)$y = 1$ 时在$\left( {x, t} \right)$ 平面上的演化图和相应的等高线图; (b), (e)$t = 0$ 时在$\left( {x, y} \right)$ 平面上的演化图和相应的等高线图; (c), (f)$ x=0 $ 时在$ (y, t) $ 平面的演化图和相应的等高线图Fig. 3. Cross-sections of two-dimensional rogue wave propagations (top row) and contour plots (bottom row) for the density distribution
${\left| {u\left( {x, y, t} \right)} \right|^2}$ given in Eq. (22) for${\rho _0} = 1.5,\; \alpha = {\left| \omega \right|^{ - 1}} = 1,\; n = 1$ with$k = 0$ : (a), (d)$\left( {x, t} \right)$ -plane with$y = 1$ ; (b), (e)$\left( {x, y} \right)$ -space with$t = 0$ ; (c), (f)$\left( {y, t} \right)$ -plane with$x = 0$ .
图 4
${\rho _0} = 1.5,\; \alpha = {\left| \omega \right|^{ - 1}} = 1$ ,$n = 1$ ,$k = 1$ 时, 由(22)式所确定的二维怪波激发 (a), (d)$y = 1$ 时在$\left( {x, t} \right)$ 平面上的演化图和相应的等高线图; (b), (e)$t = 0$ 时在$\left( {x, y} \right)$ 平面上的演化图和相应的等高线图; (c), (f)$x = 0$ 时在$\left( {y, t} \right)$ 平面的演化图和相应的等高线图Fig. 4. Cross-sections of two-dimensional rogue wave propagations (top row) and contour plots (bottom row) for the density distribution
${\left| {u\left( {x, y, t} \right)} \right|^2}$ given in Eq. (22) for${\rho _0} = 1.5$ ,$\alpha = {\left| \omega \right|^{ - 1}} = 1,\; n = 1$ with$k = 1$ : (a), (d)$\left( {x, t} \right)$ -plane with$y = 1$ ; (b), (e)$\left( {x, y} \right)$ -space with$t = 0$ ; (c), (f)$\left( {y, t} \right)$ -plane with$x = 0$ .
图 5
${\rho _0} = 1.5,\; \alpha = {\left| \omega \right|^{ - 1}} = 1,\; n = 2,\; k = 2$ 时, 由(22)式所确定的二维怪波激发 (a), (d)$y = 0$ 时在$\left( {x, t} \right)$ 平面上的演化图和相应的等高线图; (b), (e)$t = 0$ 时在$\left( {x, y} \right)$ 平面上的演化图和相应的等高线图; (c), (f)$x = 0$ 时在$\left( {y, t} \right)$ 平面的演化图和相应的等高线图Fig. 5. Cross-sections of two-dimensional rogue wave propagations (top row) and contour plots (bottom row) for the density distribution
${\left| {u\left( {x, y, t} \right)} \right|^2}$ given in Eq. (22) for${\rho _0} = 1.5,\; \alpha = {\left| \omega \right|^{ - 1}} = 1,\; n = 2$ with$k = 2$ : (a), (d)$\left( {x, t} \right)$ -plane with$y = 0$ ; (b), (e)$\left( {x, y} \right)$ -space with$t = 0$ ; (c), (f)$\left( {y, t} \right)$ -plane with$x = 0$ .
图 6 由(22)式确定的二维怪波在
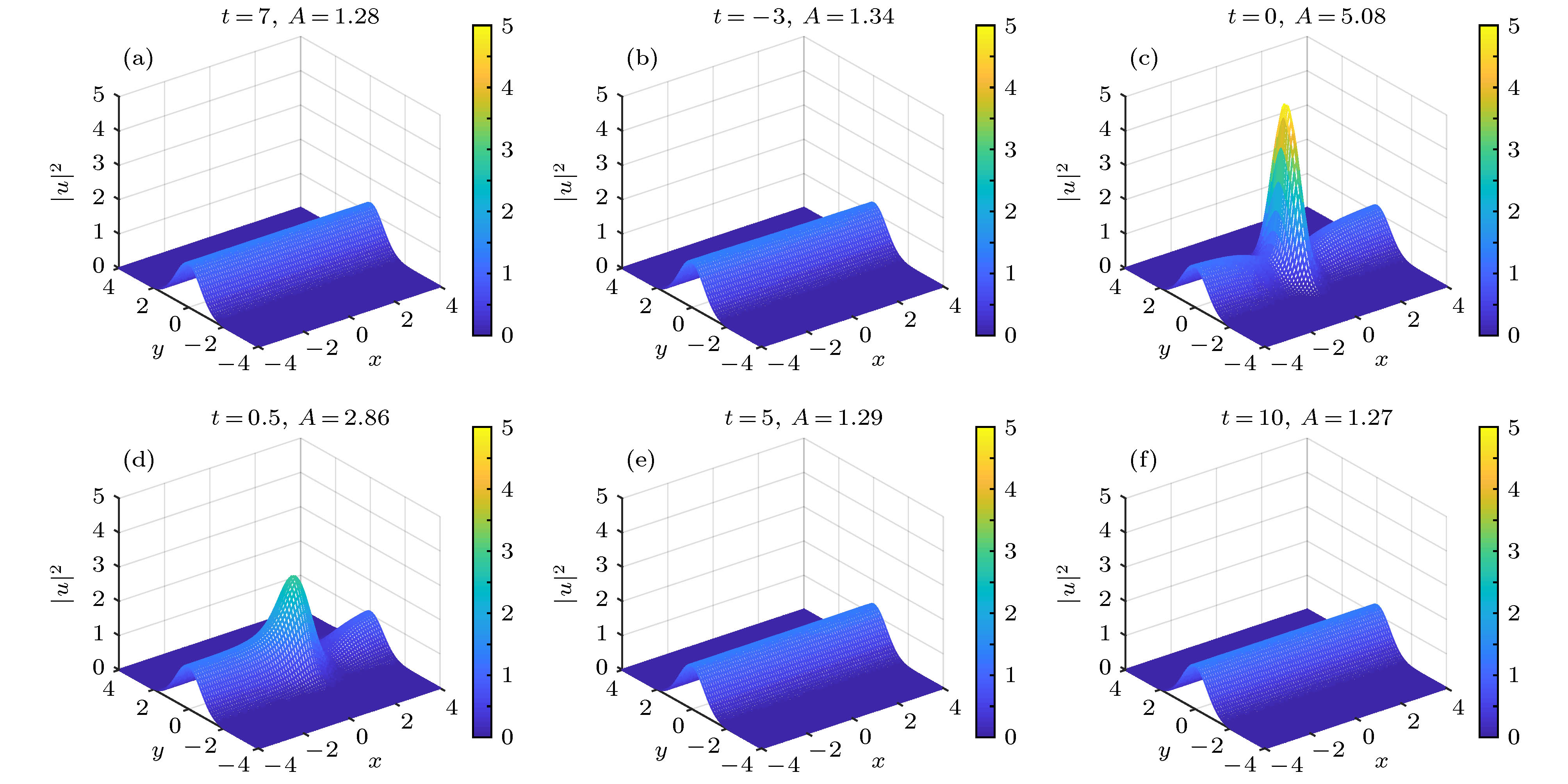
$\left( {x, t} \right)$ 平面上的演化(这里取${\rho _0}{{ = 1}}{{.5}}$ ,$\alpha = {\left| \omega \right|^{ - 1}} = 1,\; n = 0$ ,$k = 3$ ) (a)$t = - 7$ ; (b)$t = - 3$ ; (c)$t = 0$ ; (d)$t = 0.5$ ; (e)$t = 5$ ; (f)$t = 10$ Fig. 6. Cross-sections of two-dimensional wave propagations (top row) for the density distribution
${\left| {u\left( {x, y, t} \right)} \right|^2}$ given in Eq. (22) for${\rho _0} = 1.5,\; \alpha = {\left| \omega \right|^{ - 1}} = 1,\; n = 0$ with$k = 3$ : (a)$t = - 7$ ; (b)$t = - 3$ ; (c)$t = 0$ ; (d)$t = 0.5$ ; (e)$t = 5$ ; (f)$t = 10$ .
图 7 由(22)式确定的二维怪波在
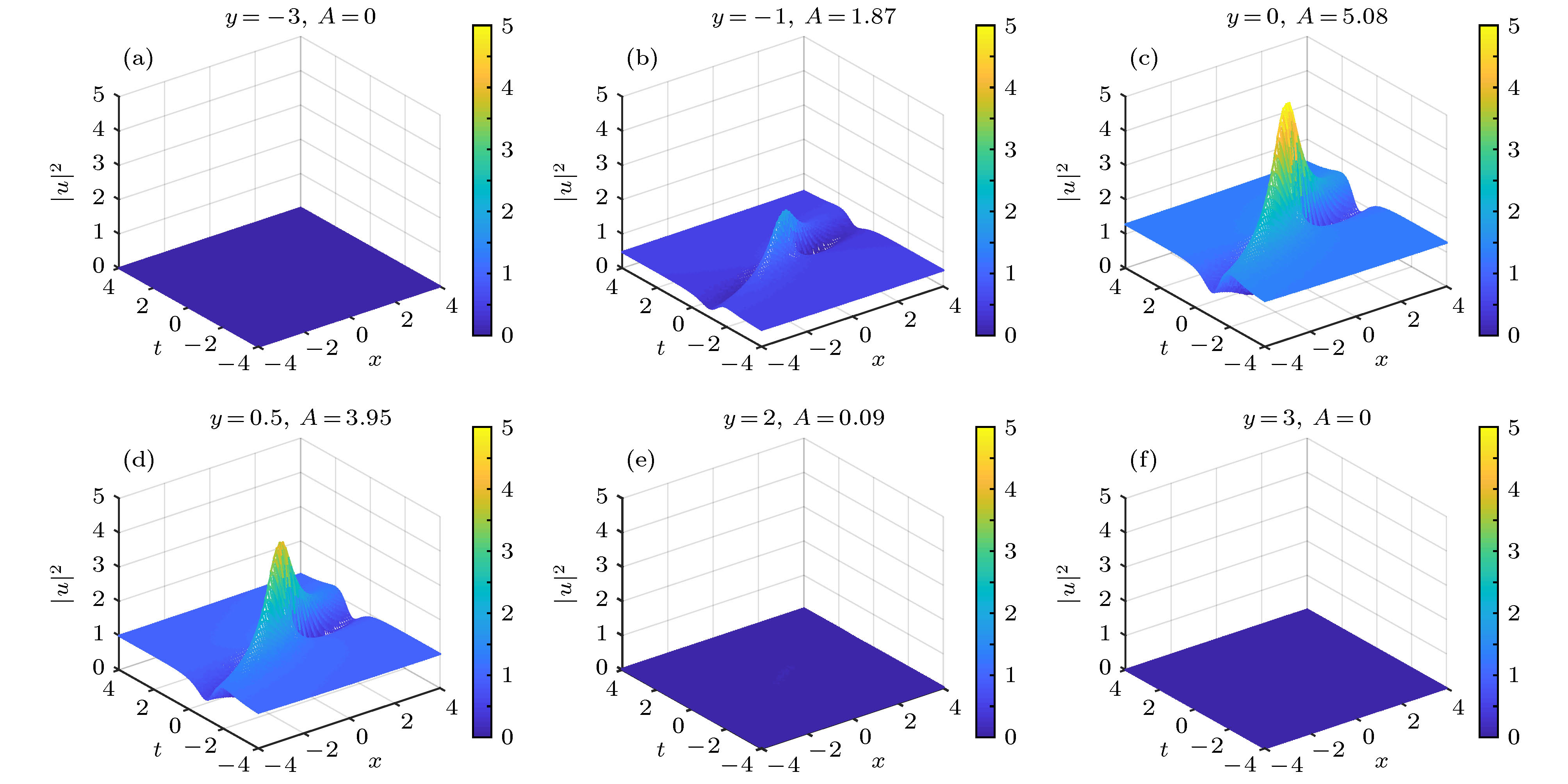
$\left( {x, t} \right)$ 平面上的演化(这里取${\rho _0}{{ = 1}}{{.5}}$ ,$\alpha = {\left| \omega \right|^{ - 1}} = 1,\; n = 0$ ,$k = 3$ ) (a)$y = - 3$ ; (b)$y = -1$ ; (c)$y = 0$ ; (d)$y = 0.5$ ; (e)$y = 2$ ; (f)$y = 3$ Fig. 7. Cross-sections of two-dimensional rogue wave propagations (top row) for the density distribution
${\left| {u\left( {x, y, t} \right)} \right|^2}$ given in Eq. (22) for${\rho _0} = 1.5,\; \alpha = {\left| \omega \right|^{ - 1}} = 1,\; n = 0$ with$k = 3$ : (a)$y = - 3$ ; (b)$y = - 1$ ; (c)$y = 0$ ; (d)$y = 0.5$ ; (e)$y = 2$ ; (f)$y = 3$ . -
[1] Pelinovsky E and Kharf C 2008 Extreme Ocean Waves (Berlin: Springer)
[2] Solli R, Ropers C, Koonath P, Jalali B 2007 Nature 450 1054
Google Scholar
[3] Montina A, Bortolozzo U, Residori S, Arecchi F T 2009 Phys. Rev. Lett. 103 173901
Google Scholar
[4] Wabnitz S 2013 J. Opt. 15 064002
Google Scholar
[5] Moslem W M 2011 Phys. Plasm. 18 032301
Google Scholar
[6] Laveder D, Passot T T, Sulem P, Sánchez Arriaga G 2011 Phys. Lett. A 375 3997
Google Scholar
[7] Bludov Yu V, Konotop V V, Akhmediev N 2009 Phys. Rev. A 80 033610
Google Scholar
[8] Efimov V B, Ganshin A N, Kolmakov G V, Mcclintock P V E, Mezhov Deglin L P 2010 Eur. Phys. J. Special Topics 185 181
Google Scholar
[9] Shats M, Punzmann H, Xia H 2010 Phys. Rev. Lett. 104 104503
Google Scholar
[10] Xia H, Maimbourg T, Punzmann H, Shats M 2012 Phys. Rev. Lett. 109 114502
Google Scholar
[11] Vergeles S, Turitsyn S K 2011 Phys. Rev. A 83 061801
Google Scholar
[12] Stenflo L, Marklund M 2010 J. Plasma Phys. 76 293
Google Scholar
[13] Yan Z Y 2010 Commun. Theor. Phys. 54 947
Google Scholar
[14] Demircan A, Amiranashvili S, Brée C, Mahnke C, Mitschke F, Steinmeyer G 2012 Sci. Rep. 2 850
Google Scholar
[15] Driben R, Babushkin I 2012 Opt. Lett. 37 5157
Google Scholar
[16] Marsal N, Caullet V, Wolfersberger D, Sciamanna M 2014 Opt. Lett. 39 3690
Google Scholar
[17] Residori S, Bortolozzo U, Montina A, Lenzini F, Arecchi F T 2012 Fluctuation Noise Lett. 11 1240014
Google Scholar
[18] Soto Crespo J M, Grelu P, Akhmediev N 2011 Phys. Rev. E 84 016604
Google Scholar
[19] Zamora M. J, Garbin B, Barland S, Giudici M, Rios Leite J R, Masoller C, Tredicce J R 2013 Phys. Rev. A 87 035802
Google Scholar
[20] Lecaplain C, Grelu P, Soto Crespo J M, Akhmediev N 2012 Phys. Rev. Lett. 108 233901
Google Scholar
[21] Buccoliero D, Steffensen H, Ebendorff Heidepriem H, Monro T M, Bang O 2011 Opt. Express 19 17973
Google Scholar
[22] Finot C, Hammani K, Fatome J, Dudley J M, Millot G 2010 IEEE J. Quantum Electron. 46 205
Google Scholar
[23] Hammani K, Finot C 2012 Opt. Fiber Technol. 18 93
Google Scholar
[24] Majus D, Jukna V, Valiulis G, Faccio D, Dubietis A 2011 Phys. Rev. A 83 025802
Google Scholar
[25] Hammani K, Finot C, Millot G 2009 Opt. Lett. 34 1138
Google Scholar
[26] Antikainen A, Erkintalo M, Dudley J M, Genty G 2012 Nonlinearity 25 73
Google Scholar
[27] Akhmediev N, Dudley J M, Solli D R, Turitsyn S K 2013 J. Opt. 15 060201
Google Scholar
[28] Chabchoub A, Hoffmann N P, Akhmediev N 2011 Phys. Rev. Lett. 106 204502
Google Scholar
[29] Bailung H, Sharma S K, Nakamura Y 2011 Phys. Rev. Lett. 107 255005
Google Scholar
[30] Randoux S, Suret P 2012 Opt. Lett. 37 500
Google Scholar
[31] 潘昌昌, Baronio F, 陈世华 2020 69 010504
Google Scholar
Pan C C, Baronio F, Chen S H 2020 Acta Phys. Sin. 69 010504
Google Scholar
[32] 李再东, 郭奇奇 2020 69 017501
Google Scholar
Li Z D and Guo Q Q 2020 Acta Phys. Sin. 69 017501
Google Scholar
[33] 陈智敏, 段文山 2020 69 014701
Google Scholar
Chen Z M, Duan W S 2020 Acta Phys. Sin. 69 014701
Google Scholar
[34] 李淑青, 杨光晔, 李禄 2014 63 104215
Google Scholar
Li S Q, Yang G Y, Li L 2014 Acta Phys. Sin. 63 104215
Google Scholar
[35] 张解放, 戴朝卿 2016 65 050501
Google Scholar
Zhang J F, Dai C Q 2016 Acta Phys. Sin. 65 050501
Google Scholar
[36] 胡文成, 张解放, 赵辟, 楼吉辉 2013 62 024216
Google Scholar
Hu W C, Zhang J F, Zhao B, Lou J H 2013 Acta Phys. Sin. 62 024216
Google Scholar
[37] Fokas A S 1994 Inverse Problems 10 19
Google Scholar
[38] Chen J C, Chen Y 2014 J. Nonlinear Math. Phys. 21 454
Google Scholar
[39] Radha R, Lakshmanan M 1997 Chaos, Solitons and Fractals 8 17
Google Scholar
[40] Villarroel J, Prada J, Estévez P G 2009 Stud. Appl. Math. 122 395
Google Scholar
[41] Estévez P G 1999 J. Math. Phys. 40 1406
Google Scholar
[42] Rao J G, Wang L H, Zhang Y, He J S 2015 Commun. Theor. Phys. 64 605
Google Scholar
[43] Chen T T, Hu P Y, He J S 2019 Commun. Theor. Phys. 71 496
Google Scholar
[44] Rao J G, Mihalacheb D, Cheng Y, He J S 2019 Phys.Lett. A 383 1138
Google Scholar
[45] Yan Z Y 2011 J. Math. Anal. Appl. 380 689
[46] Benney D J 1976 Stud. Appl. Math. 55 93
Google Scholar
[47] Kivshar Yu S 1992 Opt. Lett. 17 1322
Google Scholar
[48] Chowdhury A, Tataronis J A 2008 Phys. Rev. Lett. 100 153905
Google Scholar
[49] Zakharov V E 1972 Sov. Phys. JETP 35 908
Google Scholar
[50] Benney D J 1977 Stud. Appl. Math. 56 81
Google Scholar
[51] Djordjevic V D, Redekopp L G 1977 J. Fluid Mech. 79 703
Google Scholar
[52] Ma Y C, Redekopp L G 1979 Phys. Fluids 22 1872
Google Scholar
[53] Chow K W, Chan H N, Kedziora D J, Grimshaw R H J 2013 J. Phys. Soc. Jpn. 82 074001
Google Scholar
[54] Chen S H, Grelu P, Soto Crespo J M 2014 Phys. Rev. E 89 011201
Google Scholar
[55] Abramowitz M, Stegun I A 1965 Handbook of Mathematical Functions (New York: Dover Publications)
下载:
计量
- 文章访问数: 5624
- PDF下载量: 74
- 被引次数: 0
