-
由于电场强度能够影响铁电材料的极化强度和介电常数, 因此唯象系数
$ {a}_{0} $ 是电场强度的隐函数. 在铁电相区域, 唯象系数$ {a}_{0} $ 由铁电极化强度和介电常数倒数确定, 是电场的非线性函数. 在顺电相区域, 唯象系数$ {a}_{0} $ 由介电常数倒数确定, 也是电场的非线性函数. 本文研究了铁电共聚物、铁电三聚物和钛酸锶钡钙陶瓷的唯象系数与电场的关系, 发现唯象系数随电场的增加而增加, 最大约1倍. 电卡强度被用来表征电卡材料在电场作用下的电卡效应强弱, 通过研究电卡强度可以发现高效率的电卡材料. 本文通过热力学理论, 得到了电卡强度的解析表达式, 发现唯象系数、相变温度、极化强度、比热以及相变温度处的介电常数峰值, 对电卡强度具有明显的影响. 该表达式适用于一级相变材料、二级相变材料、以及弛豫型铁电体.As the electric field can affect the polarization and dielectric constant, the phenomenological coefficient a0 is an implicit function of electric field. The phenomenological coefficient a0 is determined by the polarization and the reciprocal of permittivity, and a nonlinear function of electric field in the ferroelectric phase regime. In the paraelectric phase regime, however, a0 is merely subjected to the reciprocal of permittivity, and also a nonlinear function of electric field. In this paper, we investigate the electric field dependence of phenomenological coefficient in ferroelectric copolymers, terpolymers and Ba0.85Ca0.05Sr0.1TiO3 ceramics. It is indicated that the phenomenological coefficient increases with the increasing electric field, the maximum value is obtained to be about 2 times the original value. Moreover, the electrocaloric strength is used to measure the magnitude of electrocaloric effect of electrocaloric materials in an external electric field. It can be used to find out novel and efficient electrocaloric materials through studying the electrocaloric strength. Based on the thermodynamic theory, the analytical expression of electrocaloric strength is deduced. It is found that the phenomenological coefficient, phase transition, specific heat capacity, and permittivity versus temperature peak value at the phase transition temperature have a clear influence on the electrocaloric strength. The expression can be applied to 1st order, 2nd order phase transition materials and relaxor ferroelectrics.-
Keywords:
- ferroelectrics /
- phase transition /
- electrocaloric effect /
- electrocaloric strength
[1] 莱因斯 M E, 格拉斯 A M 著 (钟维烈 译) 1989 铁电体及有关材料的原理和应用 (北京: 科学出版社) 第159—162页
Lines M E, Glass A M (translated by Zhong W L) 1989 Principles and Applications of Ferroelectrics and Related Materials (Beijing: Science Press) pp159–162 (in Chinese)
[2] Mischenko A S, Zhang Q, Scott J F, Whatmore R W, Mathur N D 2006 Science 311 1270
Google Scholar
[3] Neese B, Chu B J, Lu S G, Wang Y, Furman E, Zhang Q M 2008 Science 321 821
Google Scholar
[4] Correia T, Zhang Q 2014 Electrocaloric Materials: New Generation of Coolers (Berlin, Heidelberg, London: Springer Verlag) pp1–15
[5] Scott J F 2011 Ann. Rev. Mater. Res. 41 229
Google Scholar
[6] Lu S G, Zhang Q M 2012 J. Adv. Dielectr. 2 1230011
Google Scholar
[7] Okaya A, Barash L F 1962 Proc. IRE 50 2081
Google Scholar
[8] Lu S G, Neese B, Chu B J, Wang Y, Zhang Q M 2008 Appl. Phys. Lett. 93 042905
Google Scholar
[9] Lu S G, Xu Z K, Chen H D 2005 Phys. Rev. B 72 054120
Google Scholar
[10] Padmini P, Taylor T R, Lefevre M J, Nagra A S, York R A, Speck J S 1999 Appl. Phys. Lett. 75 3186
Google Scholar
[11] Zhi Y, Chen A, Guo R Y, Bhalla A S 2002 Appl. Phys. Lett. 81 1285
Google Scholar
[12] Ye H J, Qian X S, Jeong D Y, Zhang S J, Zhou Y, Shao W Z, Zhen L, Zhang Q M 2014 Appl. Phys. Lett. 105 152908
Google Scholar
[13] Amin A, Cross L E, Newnham R E 1981 Ferroelectrics 37 647
Google Scholar
[14] Rose M C, Cohen R E 2012 Phys. Rev. Lett. 109 209903
Google Scholar
[15] Buessem W R, Cross L E, Goswami A K 1966 J. Am. Ceram. Soc. 49 33
Google Scholar
[16] Lu S G, Rozic B, Kutnjiak Z, Zhang Q M 2011 Integr. Ferroelectr. 125 176
Google Scholar
[17] Inoue M, Tada Y, Suganuma K, Ishiguro H 2007 Polym. Degrad. Stab. 92 1833
Google Scholar
[18] Pelrine R, Kornbluh R, Pei Q B, Joseph J 2000 Science 287 836
Google Scholar
[19] 杨学良 2013 硕士学位论文 (天津: 天津师范大学)
Yang X L 2013 M. S. Thesis (Tianjin: Tianjin Normal University) (in Chinese)
[20] Lu S G, Zhang Q M 2009 Adv. Mater. 21 1983
Google Scholar
[21] Horchidan N, Ianculescu A, Vasilescu C, Deluca M, Musteata V, Ursic H, Frunza R, Malic B, Mitoseriu L 2014 J. Eur. Ceram. Soc. 34 3661
Google Scholar
[22] Moya X, Stern-Taulats E, Crossley S, González-Alonso D, Kar-Narayan S, Planes A, Mañosa L, Mathur N D 2013 Adv. Mater. 25 1360
Google Scholar
-
图 1 钛酸钡晶体极化强度(a)和介电常数倒数(b)在外电场作用下与温度的关系
Fig. 1. (a) Polarization and (b) reciprocal of permittivity of BaTiO3 as a function of temperature at various external electric fields.
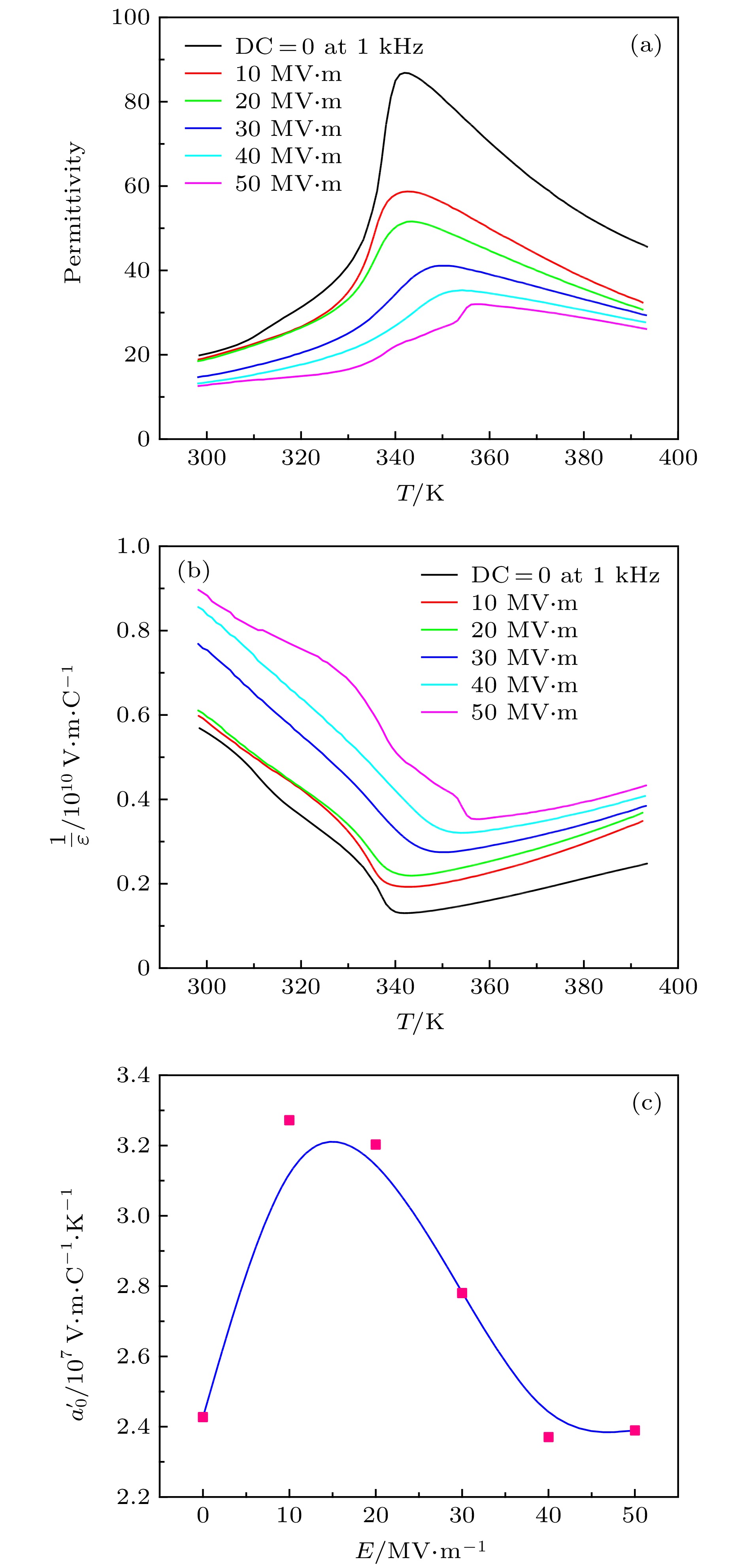
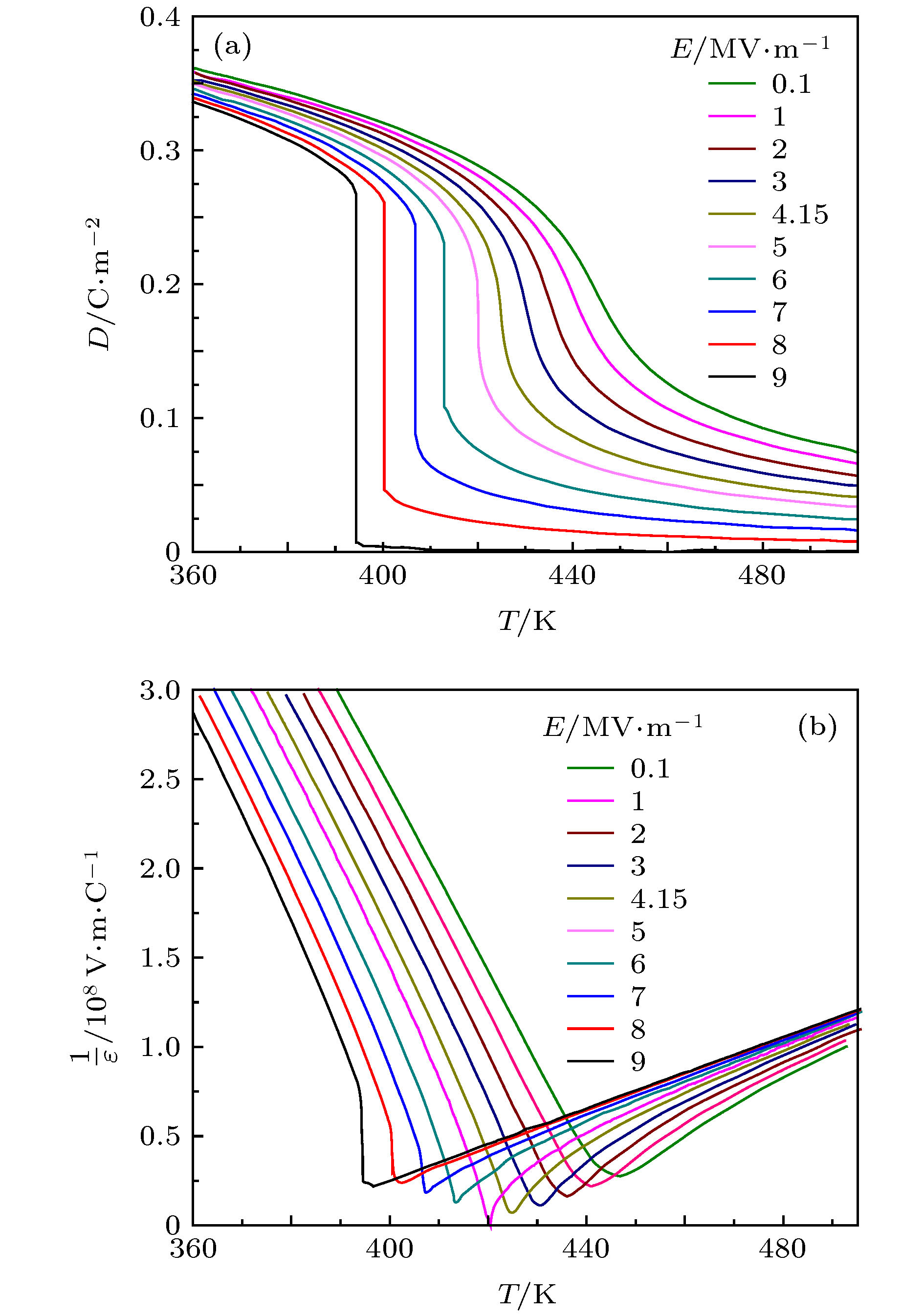
图 3 (a)聚(偏氟乙烯-三氟乙烯) 55 mol%/45 mol%共聚物介电常数与温度和电场的关系; (b)介电常数倒数与温度和电场的关系; (c)唯象系数
$ {a}_{0}' $ 与电场的关系, 图中实线是为了观察方便Fig. 3. (a) Permittivity of P(VDF-TrFE) 55 mol%/45 mol% as a function of electric field and temperature; (b) reciprocal of permittivity as a function of temperature and electric field; (c)
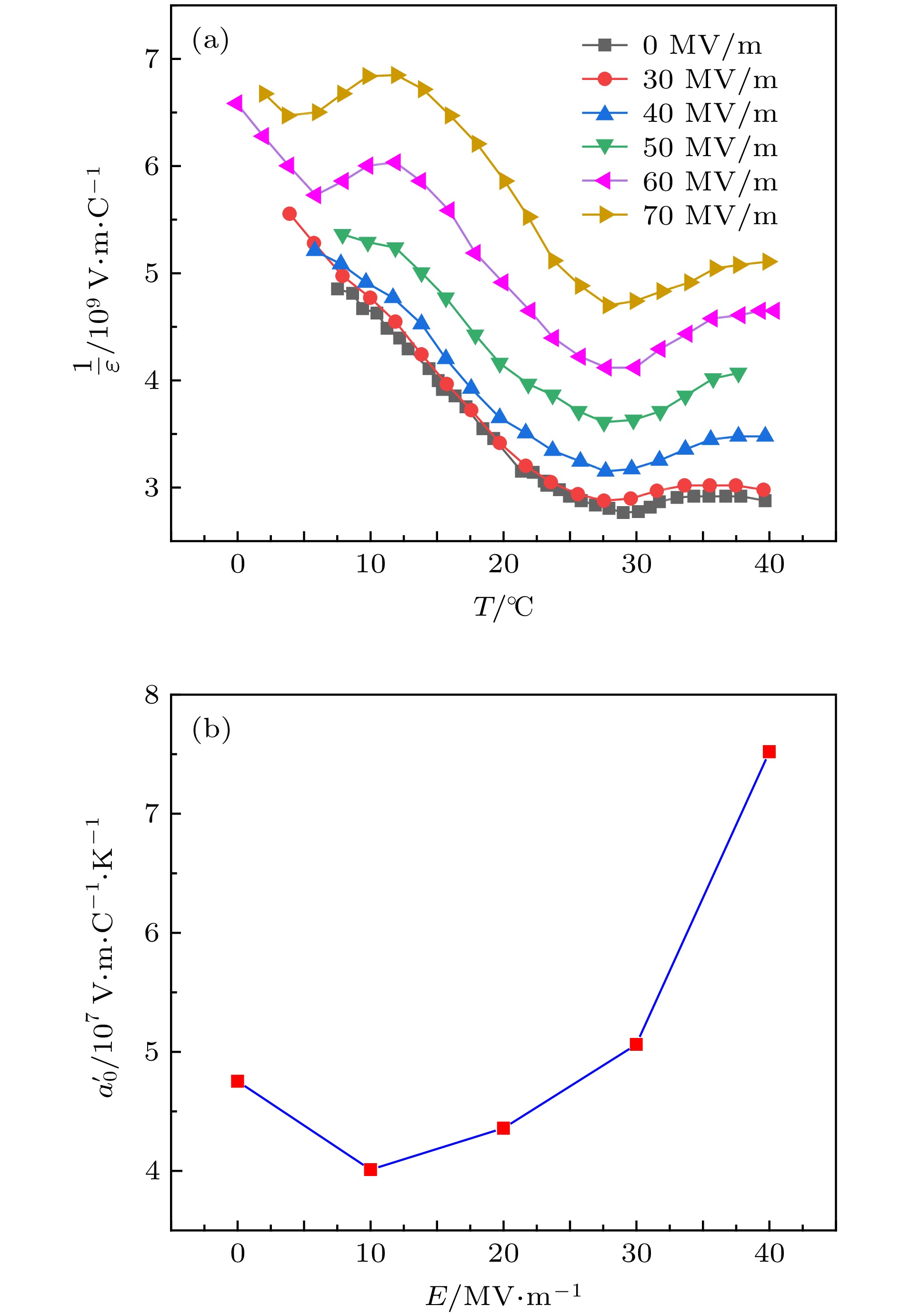
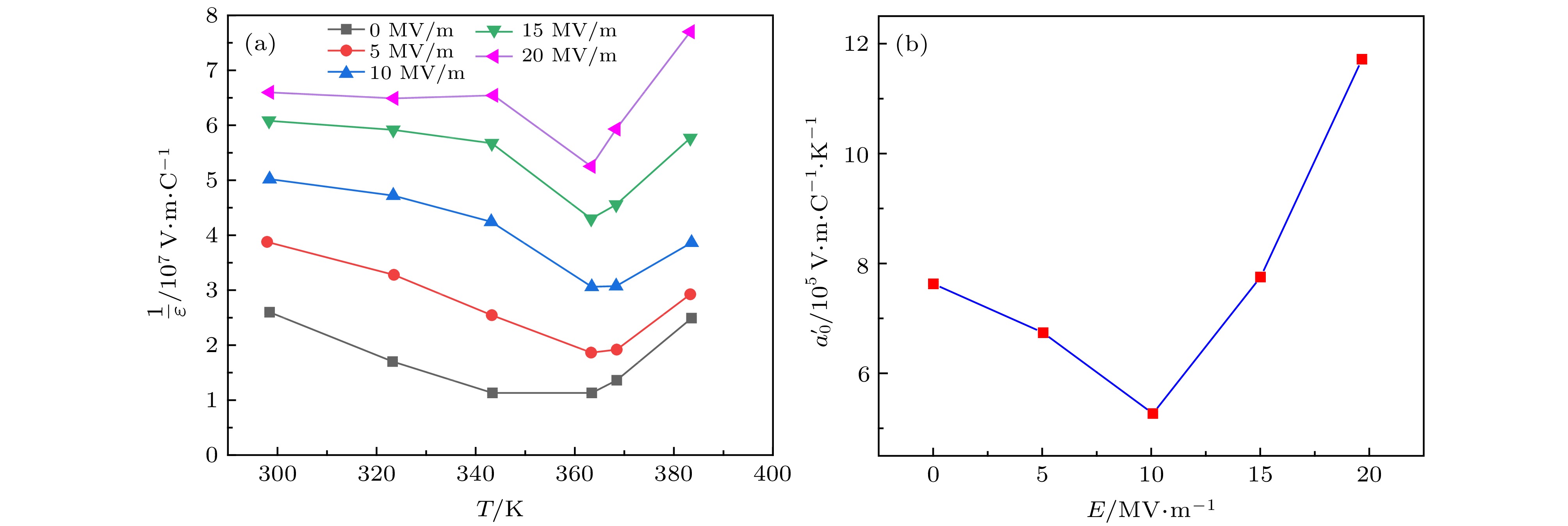
$ {a}_{0}' $ as a function of electric field and linear fitting, and the solid line occurred is guided for observation.
图 4 (a)聚(偏氟乙烯-三氟乙烯-氯氟乙烯) (P(VDF-TrFE-CFE)) 69.7 mol%/30.3 mol%/6.05 mol%三聚物介电常数倒数与温度和电场的关系; (b)相应的唯象系数
$ {a}_{0}' $ 与电场的关系Fig. 4. (a) Reciprocal of permittivity of the (P(VDF-TrFE-CFE)) 69.7 mol%/30.3 mol%/6.05 mol% as a function of temperature and electric field; (b) the corresponding
$ {a}_{0}' $ as a function of electric field.
图 5 (a) Ba0.85Ca0.05Sr0.1TiO3陶瓷介电常数倒数与温度和电场的函数关系; (b) 相应的唯象系数
$ {a}_{0}' $ 与电场的关系Fig. 5. (a) Reciprocal of permittivity of Ba0.85Ca0.05Sr0.1TiO3 ceramics as a function of temperature and electric field; (b) the corresponding
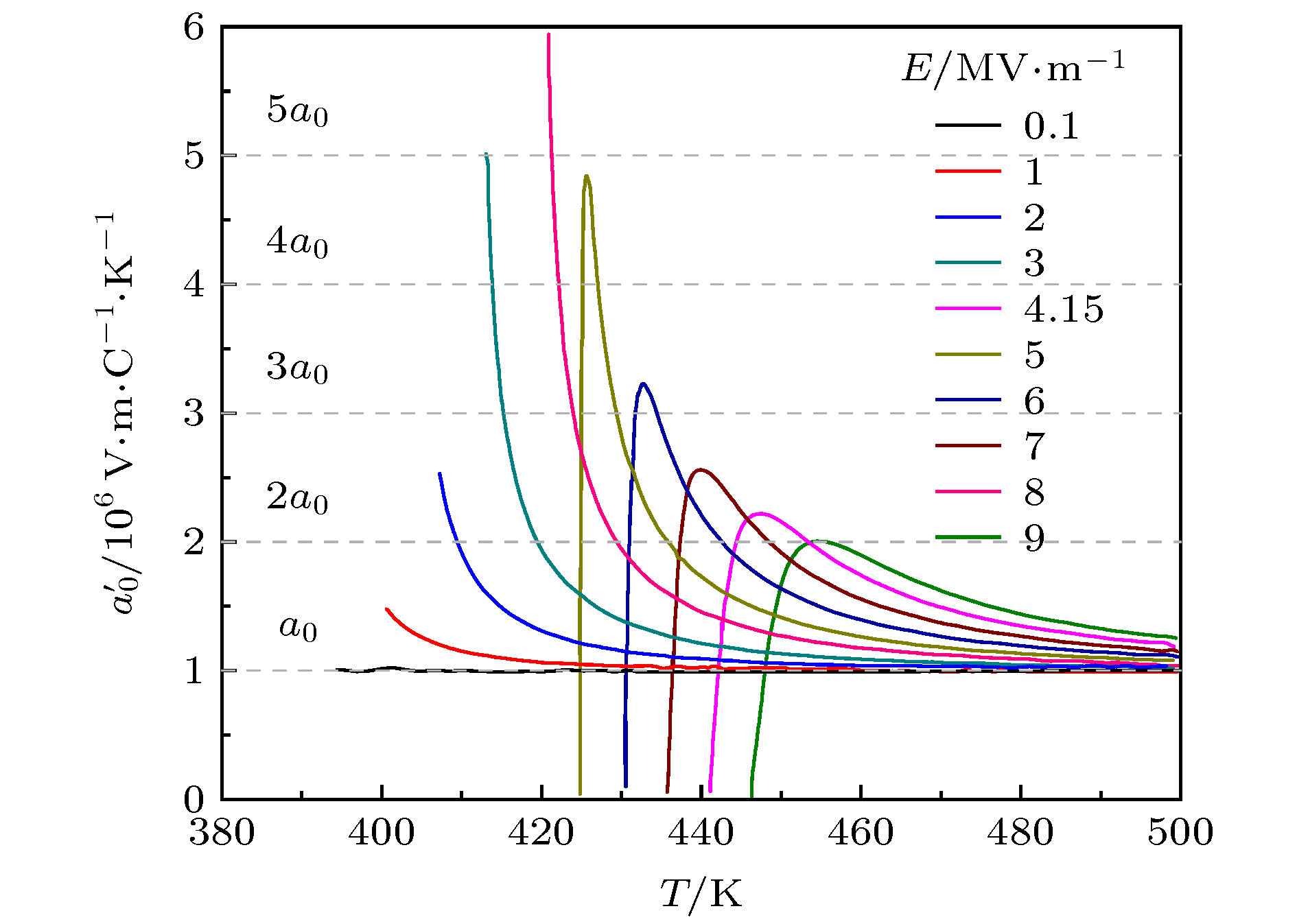
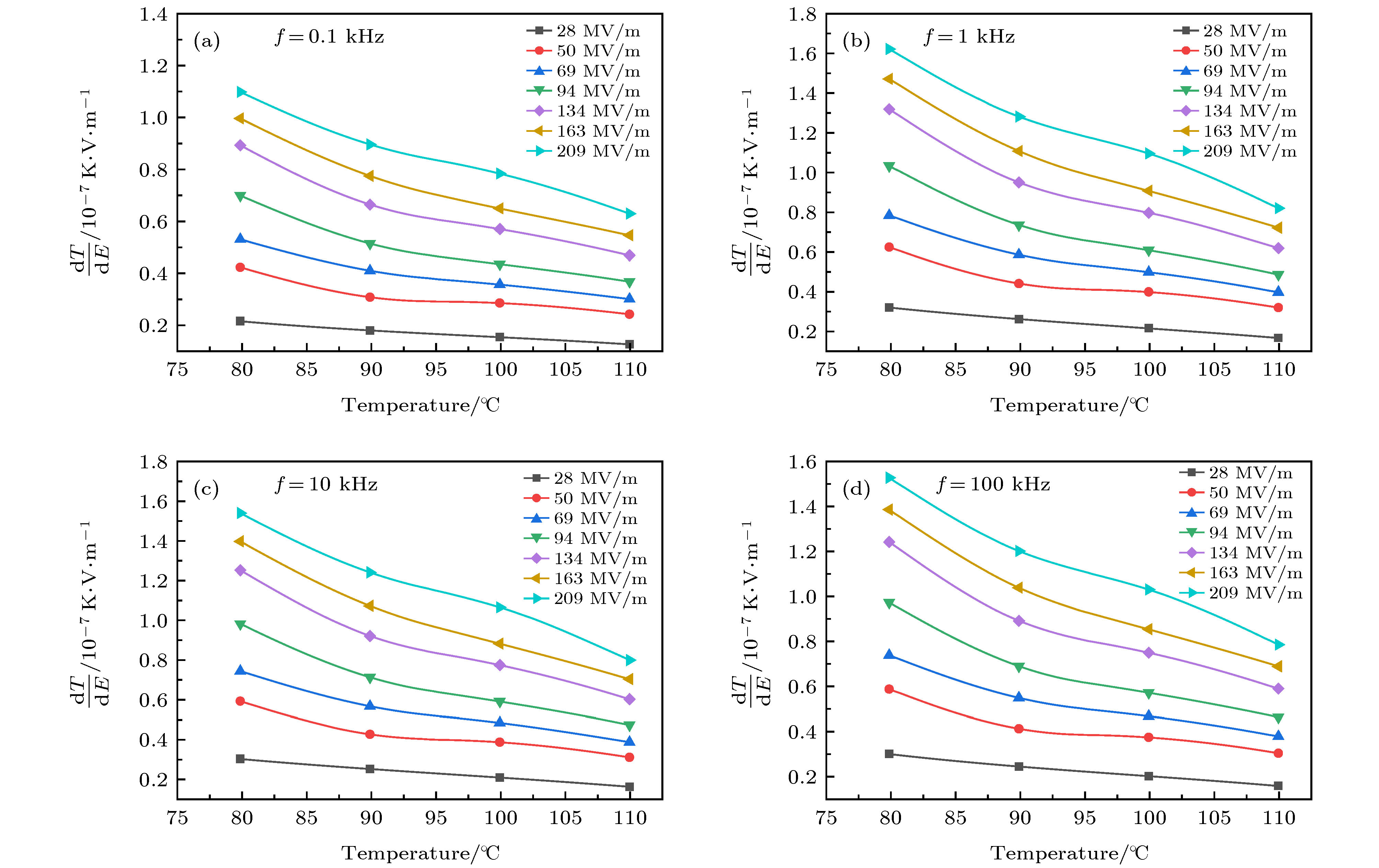
$ {a}_{0}' $ as a function of electric field.
图 6 聚(偏氟乙烯-三氟乙烯) 55 mol%/45 mol%共聚物的电卡强度(dT/dE)与温度、电场和频率的关系 (a) f = 0.1 kHz; (b) f = 1 kHz; (c) f = 10 kHz; (d) f = 100 kHz
Fig. 6. Electrocaloric strength (dT/dE) of P(VDF-TrFE) 55 mol%/45 mol% copolymer as a function of temperature, electric field and frequency: (a) f = 0.1 kHz; (b) f = 1 kHz; (c) f = 10 kHz; (d) f = 100 kHz
唯象系数符号 唯象系数数值 a0 1.15 × 106 b –5.24 × 109 c 2.16 × 1010 
下载: 导出CSV
-
[1] 莱因斯 M E, 格拉斯 A M 著 (钟维烈 译) 1989 铁电体及有关材料的原理和应用 (北京: 科学出版社) 第159—162页
Lines M E, Glass A M (translated by Zhong W L) 1989 Principles and Applications of Ferroelectrics and Related Materials (Beijing: Science Press) pp159–162 (in Chinese)
[2] Mischenko A S, Zhang Q, Scott J F, Whatmore R W, Mathur N D 2006 Science 311 1270
Google Scholar
[3] Neese B, Chu B J, Lu S G, Wang Y, Furman E, Zhang Q M 2008 Science 321 821
Google Scholar
[4] Correia T, Zhang Q 2014 Electrocaloric Materials: New Generation of Coolers (Berlin, Heidelberg, London: Springer Verlag) pp1–15
[5] Scott J F 2011 Ann. Rev. Mater. Res. 41 229
Google Scholar
[6] Lu S G, Zhang Q M 2012 J. Adv. Dielectr. 2 1230011
Google Scholar
[7] Okaya A, Barash L F 1962 Proc. IRE 50 2081
Google Scholar
[8] Lu S G, Neese B, Chu B J, Wang Y, Zhang Q M 2008 Appl. Phys. Lett. 93 042905
Google Scholar
[9] Lu S G, Xu Z K, Chen H D 2005 Phys. Rev. B 72 054120
Google Scholar
[10] Padmini P, Taylor T R, Lefevre M J, Nagra A S, York R A, Speck J S 1999 Appl. Phys. Lett. 75 3186
Google Scholar
[11] Zhi Y, Chen A, Guo R Y, Bhalla A S 2002 Appl. Phys. Lett. 81 1285
Google Scholar
[12] Ye H J, Qian X S, Jeong D Y, Zhang S J, Zhou Y, Shao W Z, Zhen L, Zhang Q M 2014 Appl. Phys. Lett. 105 152908
Google Scholar
[13] Amin A, Cross L E, Newnham R E 1981 Ferroelectrics 37 647
Google Scholar
[14] Rose M C, Cohen R E 2012 Phys. Rev. Lett. 109 209903
Google Scholar
[15] Buessem W R, Cross L E, Goswami A K 1966 J. Am. Ceram. Soc. 49 33
Google Scholar
[16] Lu S G, Rozic B, Kutnjiak Z, Zhang Q M 2011 Integr. Ferroelectr. 125 176
Google Scholar
[17] Inoue M, Tada Y, Suganuma K, Ishiguro H 2007 Polym. Degrad. Stab. 92 1833
Google Scholar
[18] Pelrine R, Kornbluh R, Pei Q B, Joseph J 2000 Science 287 836
Google Scholar
[19] 杨学良 2013 硕士学位论文 (天津: 天津师范大学)
Yang X L 2013 M. S. Thesis (Tianjin: Tianjin Normal University) (in Chinese)
[20] Lu S G, Zhang Q M 2009 Adv. Mater. 21 1983
Google Scholar
[21] Horchidan N, Ianculescu A, Vasilescu C, Deluca M, Musteata V, Ursic H, Frunza R, Malic B, Mitoseriu L 2014 J. Eur. Ceram. Soc. 34 3661
Google Scholar
[22] Moya X, Stern-Taulats E, Crossley S, González-Alonso D, Kar-Narayan S, Planes A, Mañosa L, Mathur N D 2013 Adv. Mater. 25 1360
Google Scholar
下载:
计量
- 文章访问数: 10211
- PDF下载量: 370
- 被引次数: 0
