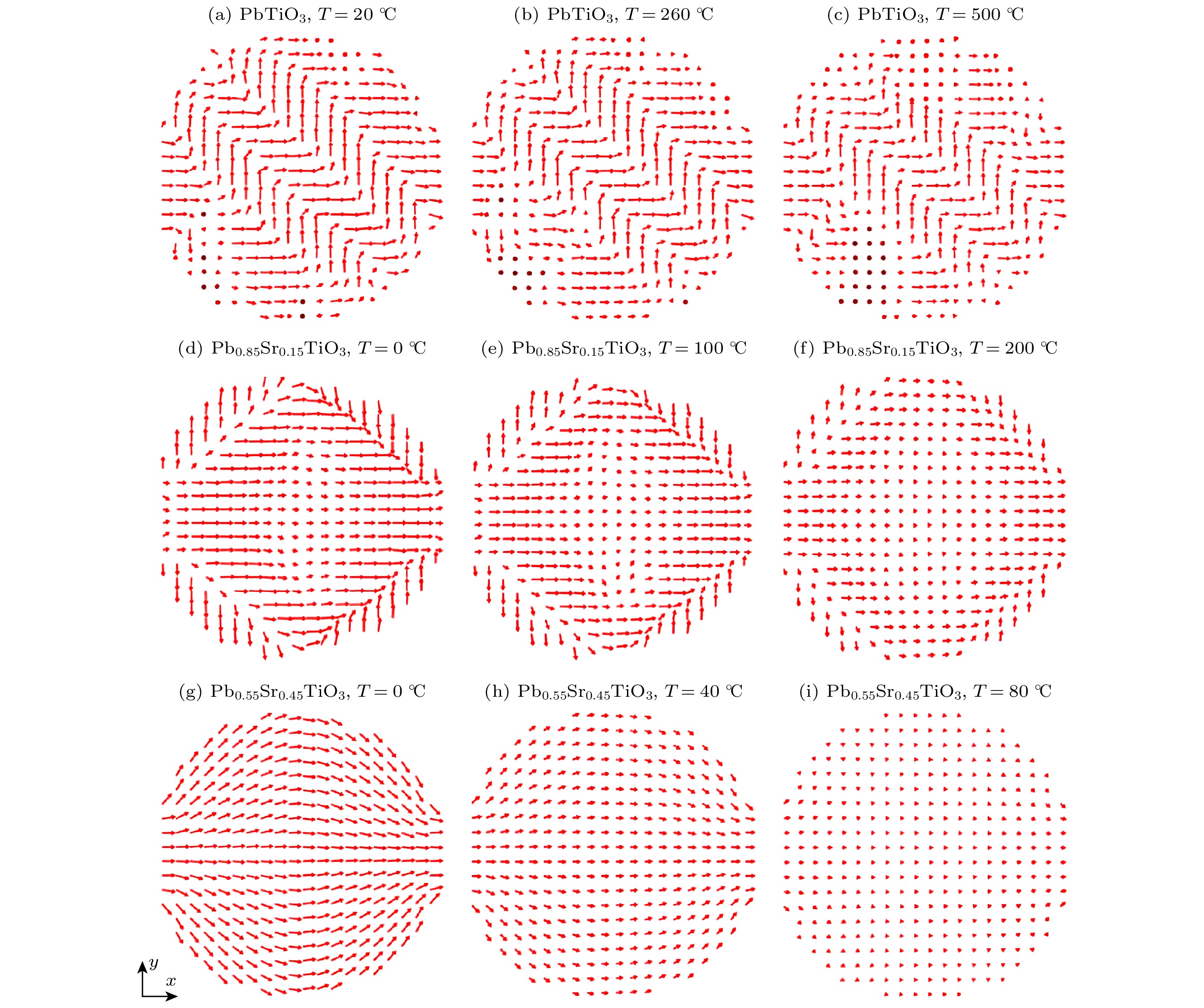
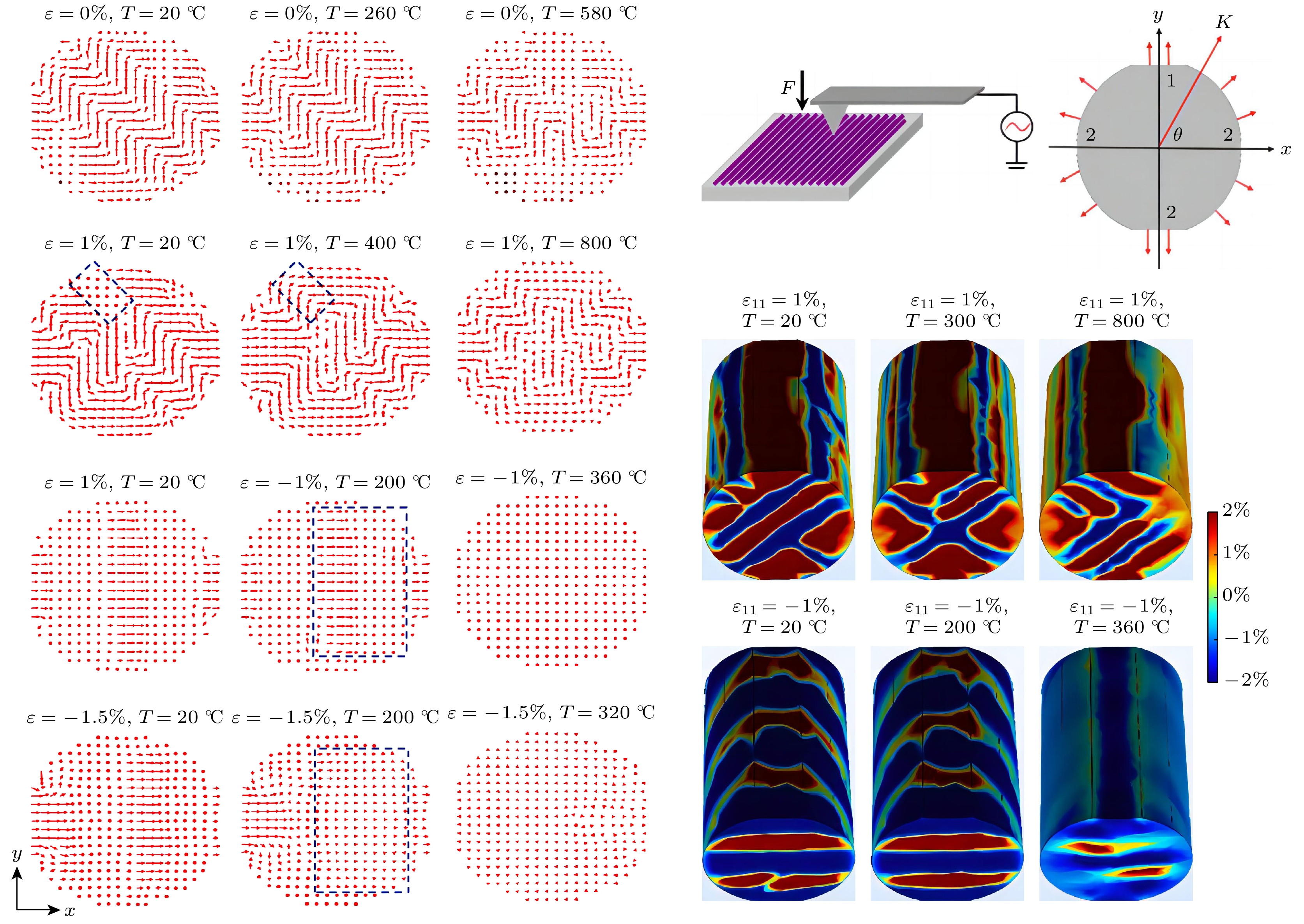
-
以铁电纳米线为填料的复合薄膜表现出了满足固态制冷需求的高绝热温变, 其平行分布填充的纳米线因和传统垂直分布的取向不同, 被认为是获得大电卡效应的关键因素, 然而其大电卡效应的内在机理尚不十分明确. 因此本文以PbTiO3纳米线为研究对象, 建立平行分布纳米线模型, 通过相场模拟研究表面应力和固溶改性对其电卡效应的影响. 结果表明, 表面应力和固溶改性能够分别调控纳米线相变温度并获取大的绝热温变, 并最终实现了在600 kV/cm电场下, 0—300 ℃的宽温度区间获得大于6 K绝热温变的效果. 同时结合三维畴结构的演变, 揭示了诱发不同畴翻转类型是平行分布纳米线结构获得大电卡效应的内在机理. 通过本研究为基于平行分布铁电纳米线电卡效应的固态制冷技术发展提供了有益的理论指导.Composite films with ferroelectric nanowires serving as fillers, exhibit high adiabatic temperature change to meet the requirement for solid-state refrigeration, and their parallel-distributed filled nanowires are considered to be the key factor because their orientation is different from the orientation of the conventional perpendicularly distributed filled nanowires. However, the underlying mechanism of the electrocaloric effect of parallel-distributed nanowires has not been well understood. In this paper, a parallel-distributed PbTiO3 nanowire model is established to investigate the effects of surface stress and solid solution modification on their electrocaloric effects through phase field simulations. The results show that an adiabatic temperature change of 5 K can be obtained near 200 ℃ with 1.5% compressive stress under an electric field of 260 kV/cm. In order to further reduce its operating temperature, the electrocaloric effects of PST nanowires with different Sr contents are calculated, and it is found that the lower the doping amount of Sr, the higher the phase transition temperature of PST nanowires is. When the doping amount of Sr is 0.45, the phase transition temperature of the nanowires can be reduced to near 100 ℃, and an adiabatic temperature change of more than 8 K can be obtained under an electric field of 600 kV/cm. Even in the low-temperature interval from 50 to 100 ℃ the nanowires exhibit an adiabatic temperature change close to 8 K. The nanowires are also characterized by an adiabatic temperature change in a low-temperature interval from 50 to 100 ℃. At the same time, by combining the evolution of the simulated three-dimensional domain structure, it is revealed that the underlying mechanism of the change of the electrocaloric effect under surface stress and solid solution modification is due to different types of domain transformations. Finally, the combinations of components and surface stresses corresponding to the maximum value of the electrocaloric effect at different operating temperatures are discussed and analyzed. The present study provides useful theoretical guidance for developing solid-state refrigeration based on parallel-distributed ferroelectric nanowires.
-
Keywords:
- electrocaloric effect /
- nanowires /
- surface stress /
- solid solution modification
[1] Neese B, Chu B J, Lu S G, Wang Y, Furman E, Zhang Q M 2008 Science 321 821
Google Scholar
[2] Valant M 2012 Prog. Mater. Sci. 57 980
Google Scholar
[3] 汤卉, 牛翔, 杨志朋, 彭小草, 赵小波, 姚英邦, 陶涛, 梁波, 唐新桂, 鲁圣国 2022 71 147701
Google Scholar
Tang H, Niu X, Yang Z P, Peng X C, Zhao X B, Yao Y B, Tao T, Liang B, Tang X G, Lu S G 2022 Acta Phys. Sin. 71 147701
Google Scholar
[4] Mischenko A S, Zhang Q, Scott J F, Whatmore R W, Mathu D N, Lu S G, Zhang Q M 2006 Science 311 1270
Google Scholar
[5] Kumar A, Kumar R, Singh K 2019 Phys. Status Solidi 216 1800786
Google Scholar
[6] 白刚, 韩宇航, 高存法 2022 71 097701
Google Scholar
Bai G, Han Y H, Gao C F 2022 Acta Phys. Sin. 71 097701
Google Scholar
[7] Ren Y Q, Qi J, Yu H D, Zhang Z, Song R Q, Song W L, Yuan B, Wang T H, Ren W J, Zhang Z D, Tong X, Li B 2022 Nat. Commun. 13 2293
Google Scholar
[8] Zhang G Z, Weng L X, Hu Z Y, Liu Y 2019 Adv. Mater. 31 1806642
Google Scholar
[9] Chen Y Q, En Y F, Huang Y, Kong X D, Zheng X J, Lu Y D 2011 Appl. Phys. Lett. 99 203106
Google Scholar
[10] Huang H B, Zhang G Z, Ma X Q, Liang D S, Wang J J, Liu Y, Wang Q, Chen L Q 2018 J. Am. Ceram. Soc. 101 1566
Google Scholar
[11] Zhu J, Chen H Y, Hou X, Xu L R, Wu H P, Wang J 2019 J. Appl. Phys. 125 234101
Google Scholar
[12] Xie B, Zhang H B, Zhang Q, Zang J D, Yang C, Wang Q P, Lia L Y, Jiang S L 2017 J. Mater. Chem. A 5 6070
Google Scholar
[13] 陶巍, 李鹏飞, 王海山 2011 机电技术 34 85
Google Scholar
Tao W, Li P F, Wang H S 2011 Mechatronic Technology 34 85
Google Scholar
[14] 仰大勇, 蒋兴宇 2008 合成纤维 37 5
Google Scholar
Yang D Y, Jiang X Y 2008 Synthetic Fibers 37 5
Google Scholar
[15] 刘迪, 王静, 王俊升 2020 69 127801
Google Scholar
Liu D, Wang J, Wang J S 2020 Acta Phys. Sin. 69 127801
Google Scholar
[16] Liu D, Zhao R, Jafri H M, Wang J S, Huang H B 2019 Appl. Phys. Lett. 114 112903
Google Scholar
[17] Haun M J, Furman E, Jang S J, Mckinstry H A, Cross L E 1987 J. Appl. Phys. 62 3331
Google Scholar
[18] Li Y L, Choudhury S, Haeni J H, et al. 2006 Phys. Rev. B 73 184112
Google Scholar
[19] Jain M, Majumder S B, Katiyar R S, Miranda F A, Van Keuls F W 2003 Appl. Phys. Lett. 821911
Google Scholar
[20] Zhu J, Chen J X, Chen H Y, Wu H P, Chen S W, Hu P Y 2022 Mech. Adv. Mater. Struc. 29 3763
Google Scholar
[21] Wang X Y, Chu R J, Dong Z C, Zhong C G, Huang Y Y, Min Y, Wang M, Zhou P X, Yuan G Q, Wei S N 2015 J. Alloys Compd. 649 261
Google Scholar
[22] Hou X, Wu H P, Li H Y, Chen H Y, Wang J 2018 J. Phys. Condens. Matter. 30 465401
Google Scholar
[23] Le V L, Hou X, Phan M H, Bui T Q, Wang J, Shimada T, Kitamura T, Dinh V H 2021 J. Phys. D Appl. Phys. 54 255307
Google Scholar
[24] Le V L, Vu N L, Ha M T, Bui T Q, Le V T, Nguyen T G, Dinh V H 2020 J. Appl. Phys. 127 214103
Google Scholar
-
图 2 纳米线模型的表面应力分布 (a) 纳米线薄膜的堆叠结构; (b)受力分析
Fig. 2. Surface stress distribution of nanowires model: (a) Stacked structure of nanowire films; (b) force analysis.
图 3 260 kV/cm电场作用下, 不同表面应力PTO纳米线的极化(a)和ΔT (b)随温度的变化
Fig. 3. Polarization (a) and ΔT (b) versus temperature of PTO nanowires with different surface strains at the electric field of 260 kV/cm
图 4 不同表面应力下PTO纳米线随温度变化的三维畴结构 (a)—(c) ε = 0; (d)—(f) ε = 1%; (g)—(i) ε = –1%; (j)—(l) ε = –1.5%
Fig. 4. Three-dimensional domain structure of PTO nanowires at different surface strains with temperature variation: (a)–(c) ε = 0; (d)–(f) ε = 1%; (g)–(i) ε = –1%; (j)–(l) ε = –1.5%.
图 5 不同表面应力下PTO纳米线随温度变化的ε11分布 (a)—(c) ε11 = 1%; (d)—(f) ε11 = –1%
Fig. 5. ε11 distribution of PTO nanowires at different surface strains with temperature variation: (a)–(c) ε11 = 1%; (d)–(f) ε11 = –1%.
图 6 在600 kV/cm电场作用下不同Pb/Sr比例纳米线的极化(a)和ΔT (b)随温度变化关系
Fig. 6. Polarization (a) and ΔT (b) versus temperature of nanowires with different Pb/Sr ratios at the electric field of 600 kV/cm.
图 7 不同Pb/Sr比的PST纳米线随温度变化的三维畴结构 (a)—(c) PTO; (d)—(f) Pb0.85Sr0.15TiO3; (g)—(i) Pb0.55Sr0.45TiO3
Fig. 7. Three-dimensional domain structure of PST nanowires at different Pb/Sr ratios with temperature variation: (a)–(c) PTO; (d)–(f) Pb0.85Sr0.15TiO3; (g)–(i) Pb0.55Sr0.45TiO3.
图 8 表面应力下不同Pb/Sr比的纳米线的最大ΔT (a)和工作温度(b)
Fig. 8. Maximum ΔT (a) and working temperature (b) of nanowires with different Pb/Sr ratios under surface strain.
-
[1] Neese B, Chu B J, Lu S G, Wang Y, Furman E, Zhang Q M 2008 Science 321 821
Google Scholar
[2] Valant M 2012 Prog. Mater. Sci. 57 980
Google Scholar
[3] 汤卉, 牛翔, 杨志朋, 彭小草, 赵小波, 姚英邦, 陶涛, 梁波, 唐新桂, 鲁圣国 2022 71 147701
Google Scholar
Tang H, Niu X, Yang Z P, Peng X C, Zhao X B, Yao Y B, Tao T, Liang B, Tang X G, Lu S G 2022 Acta Phys. Sin. 71 147701
Google Scholar
[4] Mischenko A S, Zhang Q, Scott J F, Whatmore R W, Mathu D N, Lu S G, Zhang Q M 2006 Science 311 1270
Google Scholar
[5] Kumar A, Kumar R, Singh K 2019 Phys. Status Solidi 216 1800786
Google Scholar
[6] 白刚, 韩宇航, 高存法 2022 71 097701
Google Scholar
Bai G, Han Y H, Gao C F 2022 Acta Phys. Sin. 71 097701
Google Scholar
[7] Ren Y Q, Qi J, Yu H D, Zhang Z, Song R Q, Song W L, Yuan B, Wang T H, Ren W J, Zhang Z D, Tong X, Li B 2022 Nat. Commun. 13 2293
Google Scholar
[8] Zhang G Z, Weng L X, Hu Z Y, Liu Y 2019 Adv. Mater. 31 1806642
Google Scholar
[9] Chen Y Q, En Y F, Huang Y, Kong X D, Zheng X J, Lu Y D 2011 Appl. Phys. Lett. 99 203106
Google Scholar
[10] Huang H B, Zhang G Z, Ma X Q, Liang D S, Wang J J, Liu Y, Wang Q, Chen L Q 2018 J. Am. Ceram. Soc. 101 1566
Google Scholar
[11] Zhu J, Chen H Y, Hou X, Xu L R, Wu H P, Wang J 2019 J. Appl. Phys. 125 234101
Google Scholar
[12] Xie B, Zhang H B, Zhang Q, Zang J D, Yang C, Wang Q P, Lia L Y, Jiang S L 2017 J. Mater. Chem. A 5 6070
Google Scholar
[13] 陶巍, 李鹏飞, 王海山 2011 机电技术 34 85
Google Scholar
Tao W, Li P F, Wang H S 2011 Mechatronic Technology 34 85
Google Scholar
[14] 仰大勇, 蒋兴宇 2008 合成纤维 37 5
Google Scholar
Yang D Y, Jiang X Y 2008 Synthetic Fibers 37 5
Google Scholar
[15] 刘迪, 王静, 王俊升 2020 69 127801
Google Scholar
Liu D, Wang J, Wang J S 2020 Acta Phys. Sin. 69 127801
Google Scholar
[16] Liu D, Zhao R, Jafri H M, Wang J S, Huang H B 2019 Appl. Phys. Lett. 114 112903
Google Scholar
[17] Haun M J, Furman E, Jang S J, Mckinstry H A, Cross L E 1987 J. Appl. Phys. 62 3331
Google Scholar
[18] Li Y L, Choudhury S, Haeni J H, et al. 2006 Phys. Rev. B 73 184112
Google Scholar
[19] Jain M, Majumder S B, Katiyar R S, Miranda F A, Van Keuls F W 2003 Appl. Phys. Lett. 821911
Google Scholar
[20] Zhu J, Chen J X, Chen H Y, Wu H P, Chen S W, Hu P Y 2022 Mech. Adv. Mater. Struc. 29 3763
Google Scholar
[21] Wang X Y, Chu R J, Dong Z C, Zhong C G, Huang Y Y, Min Y, Wang M, Zhou P X, Yuan G Q, Wei S N 2015 J. Alloys Compd. 649 261
Google Scholar
[22] Hou X, Wu H P, Li H Y, Chen H Y, Wang J 2018 J. Phys. Condens. Matter. 30 465401
Google Scholar
[23] Le V L, Hou X, Phan M H, Bui T Q, Wang J, Shimada T, Kitamura T, Dinh V H 2021 J. Phys. D Appl. Phys. 54 255307
Google Scholar
[24] Le V L, Vu N L, Ha M T, Bui T Q, Le V T, Nguyen T G, Dinh V H 2020 J. Appl. Phys. 127 214103
Google Scholar
下载:
计量
- 文章访问数: 1668
- PDF下载量: 57
- 被引次数: 0
