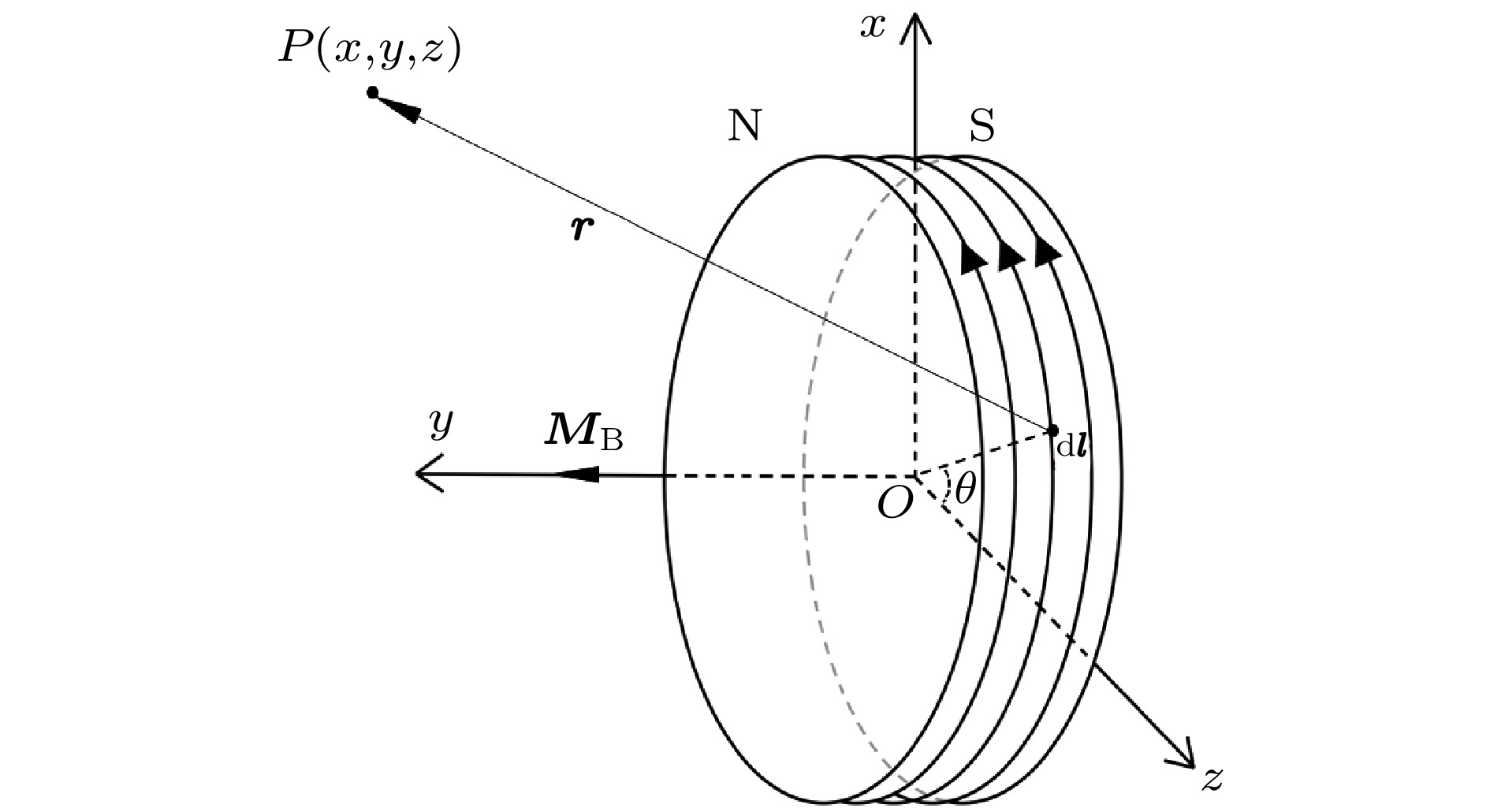
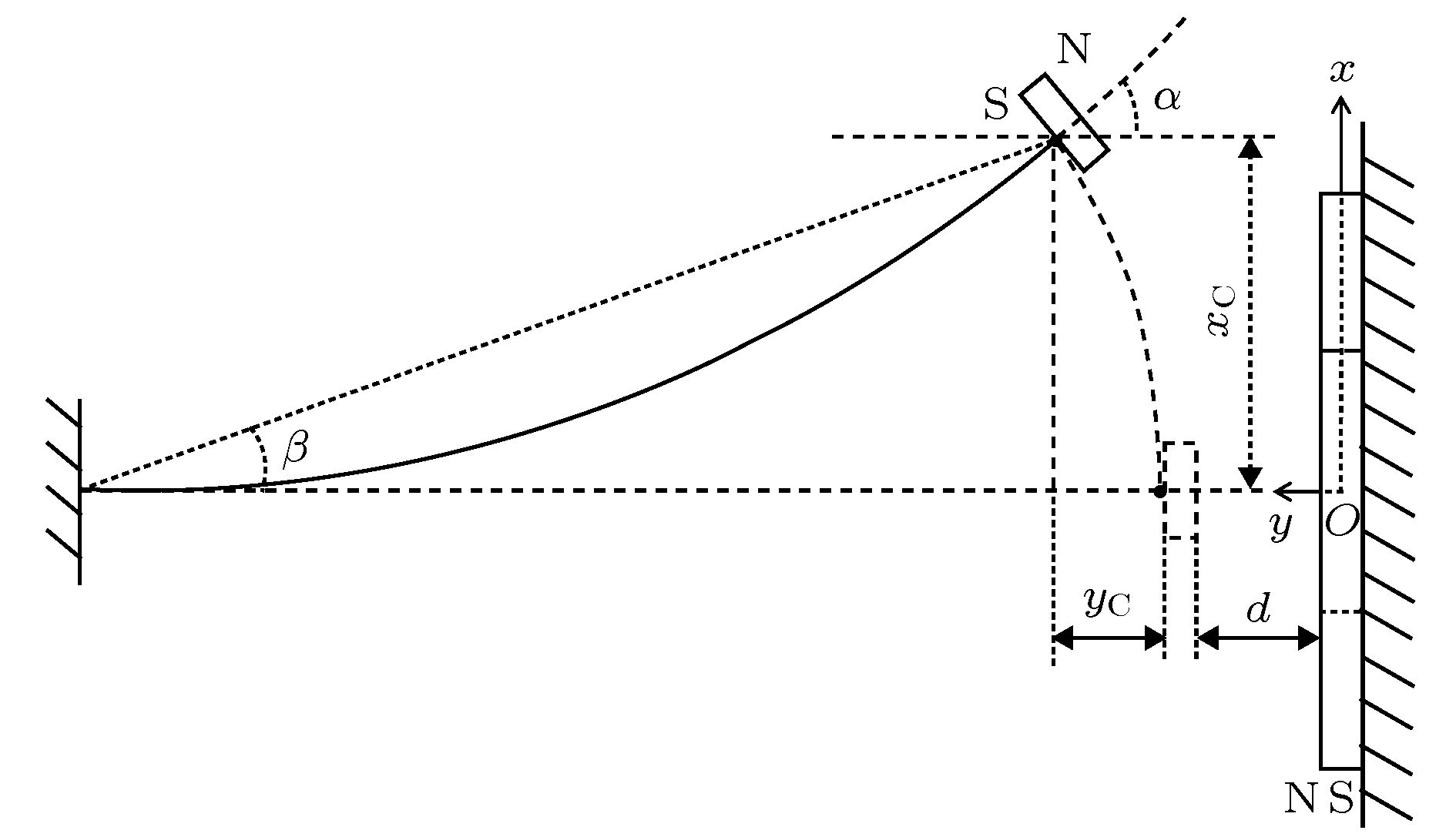
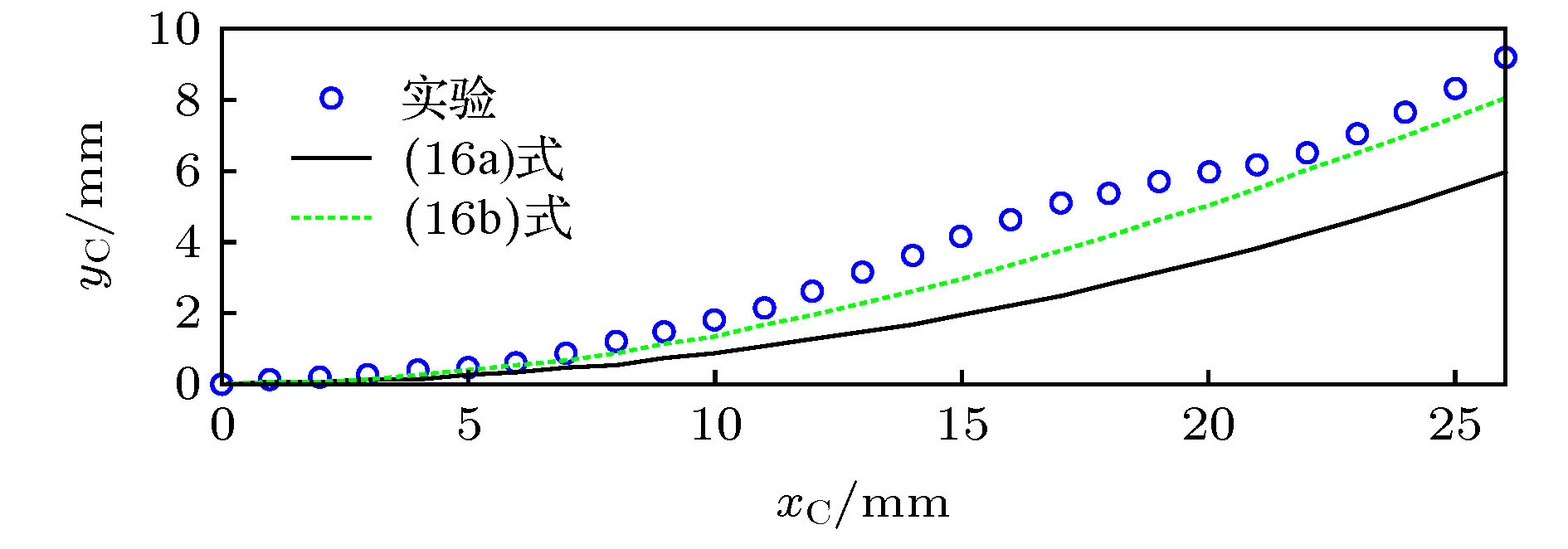
-
Multi-stable structures are deformable structures that can have large deformations under external excitation. Generally, multi-stable structures have at least two stable points and can jump from one to another. Because multi-stable structures have excellent nonlinear characteristics, they are widely used in many fields. In the field of energy harvesting, multi-stable structures are often obtained by means of cantilever beams. This is because the cantilever beam is simple to make, low in stiffness, and high in sensitivity, and can undergo large deformations under small excitation forces. Besides, by simply sticking magnets on its free end and its outside, various kinds of multi-stable characteristics can be constructed, such as bi-stable characteristics, tri-stable characteristics, quad-stable characteristics, etc. Furthermore, the cantilever beam and the magnet at its end can generally be simplified into an equivalent mass-spring-damping mechanical model, which is convenient for the analysis of system potential function and dynamics. In recent years, many vibration energy harvesters proposed by researchers have adopted the conventional multi-stable cantilever beams, which involve many bi-stable cantilever beams and tri-stable cantilever beams. However, if the cantilever beams need to introduce more stable points, the number of magnets required will also increase accordingly. As a result, the adjustable parameters are continuously increasing, which increases the complexity of structural optimization and the tediousness of dynamic analysis. In order to make up for the shortcomings of conventional multi-stable cantilever beams, in this paper we present a multi-stable cantilever beam with only two magnets, a ring magnet and a rectangular magnet. By changing the size of the rectangular magnet and the distance between the two magnets, this cantilever beam can have mono-stable, bi-stable, tri-stable or quad-stable characteristics. This multi-stable cantilever beam greatly simplifies the complexity of the system design, dynamic analysis, debugging and installation, and provides new ideas and technical methods for the design and application of the vibration energy harvester realized by the multi-stable cantilever beam. In this paper, firstly, the magnetizing current method is used to analyze the magnetic induction intensity of the ring magnet at any point in the three-dimensional coordinate system, and the simulation and experimental results prove its correctness. Secondly, two methods of calculating the position of the rectangular magnet at the free end of the cantilever beam are compared. Thirdly, the magnetic force between the ring magnet and the rectangular magnet is calculated and verified in experiment. Fourthly, the system potential functions under different structural parameters are analyzed and it is found that the change of the number of the stable points of the system is caused by the change of the magnetic force between the two magnets. Finally, the correctness of the number of stable points of the system under different parameters is verified in experiment and by dynamic simulations. -
Keywords:
- two magnets /
- multi-stable cantilever beam /
- magnetic force /
- potential function
[1] Daynes S, Weaver P M 2012 Smart Mater. Struct. 21 105019
Google Scholar
[2] Barbarino S, Bilgen O, Ajaj R M, Friswell M I, Inman D J 2011 J. Intel. Mat. Syst. Str. 22 823
Google Scholar
[3] 姜伟红 2018 硕士学位论文(哈尔滨: 哈尔滨工业大学)
Jiang W H 2018 M. S. Thesis (Harbin: Harbin Institute of Technology) (in Chinese)
[4] Diaconu C G, Weaver P M, Mattioni F 2008 Thin Wall. Struct. 46 689
Google Scholar
[5] Daynes S, Nall S J, Weaver P M, Potter K D, Margaris P, Mellor P H 2010 J. Aircraft 47 334
Google Scholar
[6] 沙山克·普利亚, 丹尼尔·茵曼(黄见秋, 黄庆安, 译) 2010 能量收集技术 (南京: 东南大学出版社) 第 1—4 页
Priya S, Inman D J (Translated by Huang J Q, Huang Q A) 2010 Energy Harvesting Technologies (Nanjing: Southeast University Press) pp1–4 (in Chinese)
[7] 卢有为, 单小彪, 袁江波, 谢涛 2010 机械设计与制造 5 118
Google Scholar
Lu Y W, Shan X B, Yuan J B, Xie T 2010 Machinery Design & Manufacture 5 118
Google Scholar
[8] 王治平, 刘俊标, 姜楠, 李博 2010 压电与声光 32 763
Wang Z P, Liu J B, Jiang N, Li B 2010 Piezoelectrics & Acoustooptics 32 763
[9] Challa V R, Prasad M G, Fisher F T 2009 Smart Mater. Struct. 18 095029
Google Scholar
[10] 陈仲生, 杨拥民 2011 60 074301
Google Scholar
Chen Z S, Yang Y M 2011 Acta Phys. Sin. 60 074301
Google Scholar
[11] Podder P, Amann A, Roy S 2015 Sensor Actuat. A-Phys. 227 39
Google Scholar
[12] Gao Y J, Leng Y G, Fan S B, Lai Z H 2014 Smart Mater. Struct. 23 095003
Google Scholar
[13] Leng Y G, Tan D, Liu J J, Zhang Y Y, Fan S B 2017 J. Sound Vib. 406 146
Google Scholar
[14] Zhou S X, Cao J Y, Inman D J, Lin J, Liu S S, Wang Z Z 2014 Appl. Energy 133 33
Google Scholar
[15] Deng W, Wang Y 2017 Mech. Syst. Signal Pr. 85 591
Google Scholar
[16] Roundy S, Wright P K, Rabaey J 2003 Comput. Commun. 26 1131
Google Scholar
[17] DuToit N E, Wardle B L 2005 Integr. Ferroelectri. 45 1126
[18] Roundy S, Wright P K 2004 Smart Mater. Struct. 13 1131
Google Scholar
[19] Agashe J S, Arnold D P 2008 J. Phys. D: Appl. Phys. 41 105001
Google Scholar
[20] 张雨阳, 冷永刚, 谭丹, 刘进军, 范胜波 2017 66 220502
Google Scholar
Zhang Y Y, Leng Y G, Tan D, Liu J J, Fan S B 2017 Acta Phys. Sin. 66 220502
Google Scholar
[21] 谭丹, 冷永刚, 范胜波, 高毓璣 2015 64 060502
Google Scholar
Tan D, Leng Y G, Fan S B, Gao Y J 2015 Acta Phys. Sin. 64 060502
Google Scholar
[22] Tan D, Leng Y G, Gao Y J 2015 Eur. Phys. J.: Spec. Top. 224 2839
Google Scholar
-
图 1 双磁铁多稳态悬臂梁 (a) 三稳状态; (b) 四稳状态
Fig. 1. Multi-stable cantilever beam with two magnets: (a) The state concluding three stable points; (b) the state concluding four stable points.
图 2 空间坐标系及圆形实心磁铁的磁化电流示意图
Fig. 2. Schematic diagram of there-dimension coordinate system and magnetizing currents on the surface of the circular magnet.
图 3 磁感应强度Bi, Bj随x的变化关系 (a) Bi随x的变化, y = 6.0 mm; (b) Bj随x的变化, y = 6.0 mm; (c) Bi随x的变化, y = 10.0 mm; (d) Bj随x的变化, y = 10.0 mm
Fig. 3. The curves of Bi and Bj varying with x: (a) The curves of Bi varying with x, y = 6.0 mm; (b) the curves of Bj varying with x, y = 6.0 mm; (c) the curves of Bi varying with x, y = 10.0 mm; (d) the curves of Bj varying with x, y = 10.0 mm.
图 4 磁感应强度测量系统 (a)Bi测量; (b)Bj测量
Fig. 4. Magnetic induction intensity measurement system: (a) The measurement of Bi; (b) the measurement of Bj.
图 5 悬臂梁弯曲状态及其矩形磁铁的坐标位置
Fig. 5. The position of the rectangular magnet in coordinate system when the cantilever beam is bent.
图 6 梁自由端磁铁位置的两种计算方法
Fig. 6. Two kinds of calculation of the position of the magnet at the free end of the beam.
图 8 矩形磁铁尺寸及磁化电流示意图
Fig. 8. Schematic diagram of the size of the rectangular magnet and the magnetizing currents on the surface of the rectangular magnet.
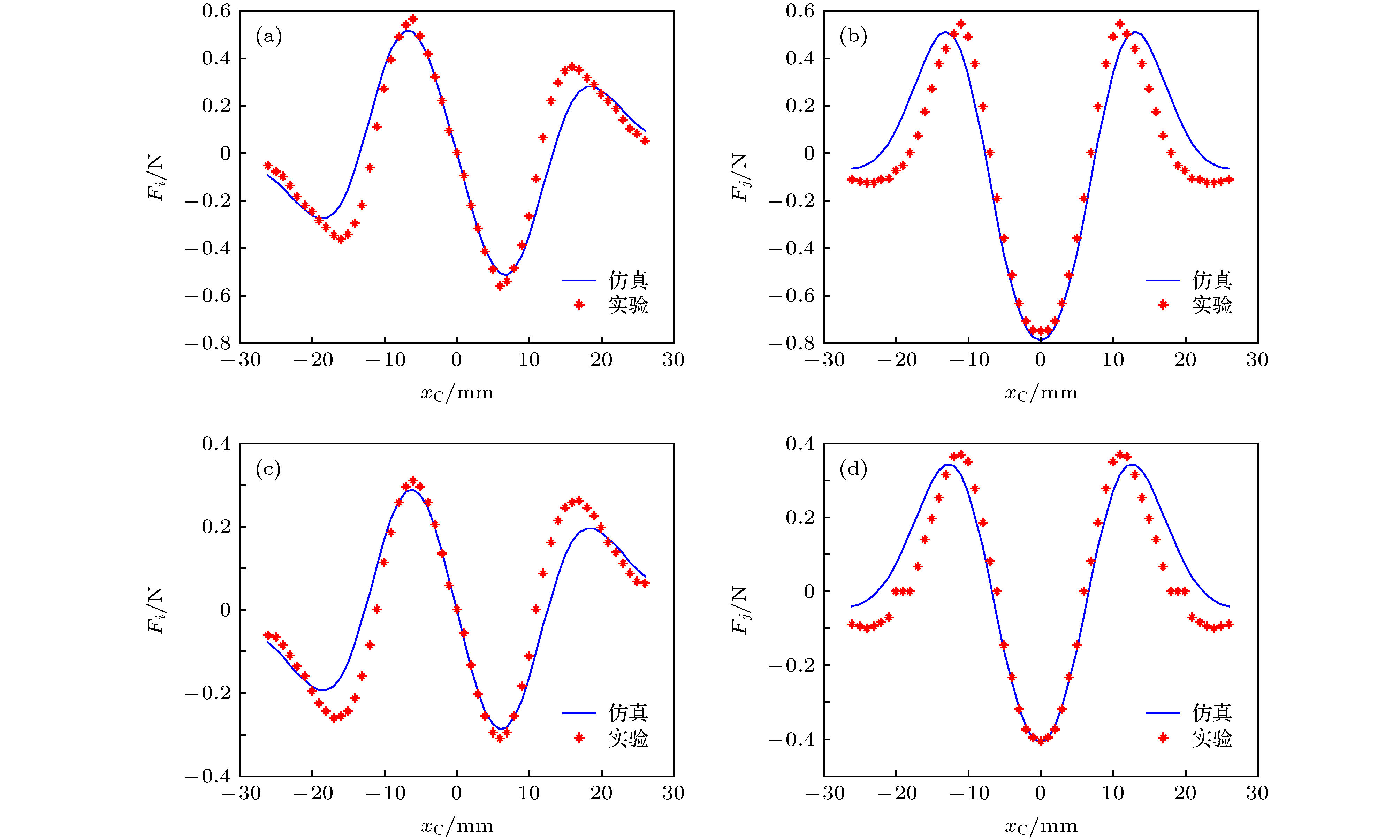
图 9 Fi, Fj随xC的变化关系 (a) Fi随xC的变化关系, d = 5.8 mm; (b)Fj随xC的变化关系, d = 5.8 mm; (c) Fi随xC的变化关系, d = 8.0 mm; (d) Fj随xC的变化关系, d = 8.0 mm
Fig. 9. The curves of Fi and Fj varying with xC: (a) The curves of Fi varying with xC, d = 5.8 mm; (b) the curves of Fj varying with xC, d = 5.8 mm; (c) the curves of Fi varying with xC, d = 8.0 mm; (d) the curves of Fj varying with xC, d = 8.0 mm.
图 10 磁力测量系统 (a) Fi 测量; (b) Fj测量
Fig. 10. Magnetic force measurement system: (a) The measurement of Fi; (b) the measurement of Fj.
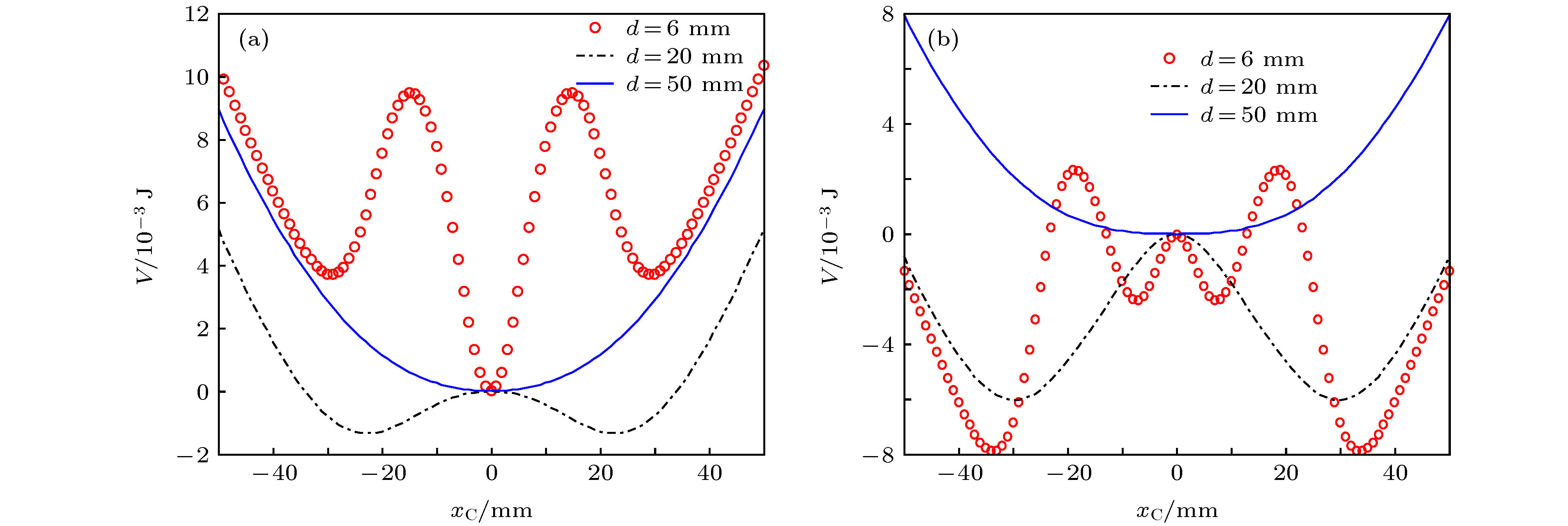
图 11 矩形磁铁(10 mm × 10 mm × 3 mm)与环形磁铁(40 mm (φ1) × 20 mm (φ2) × 3 mm)作用的系统势函数 (a)系统势函数三维图; (b)磁铁间距分别为d = 3 mm, d = 6 mm, d = 20 mm时系统势函数二维图
Fig. 11. The system potential function varying with d when the size of the rectangular magnet is 10 mm × 10 mm × 3 mm and the ring magnet is 40 mm (φ1) × 20 mm (φ2) × 3 mm: (a) Three dimensional diagram of system potential function; (b) two dimensional diagram of system potential function when d = 3 mm, d = 6 mm and d = 20 mm.
图 12 系统势函数随d的变化 (a)矩形磁铁尺寸为 20 mm × 20 mm × 3 mm; (b) 矩形磁铁尺寸为 30 mm × 30 mm × 3 mm
Fig. 12. The system potential function varying with d: (a) The size of the rectangular magnet is 20 mm × 20 mm × 3 mm; (b) the size of the rectangular magnet is 30 mm × 30 mm × 3 mm.
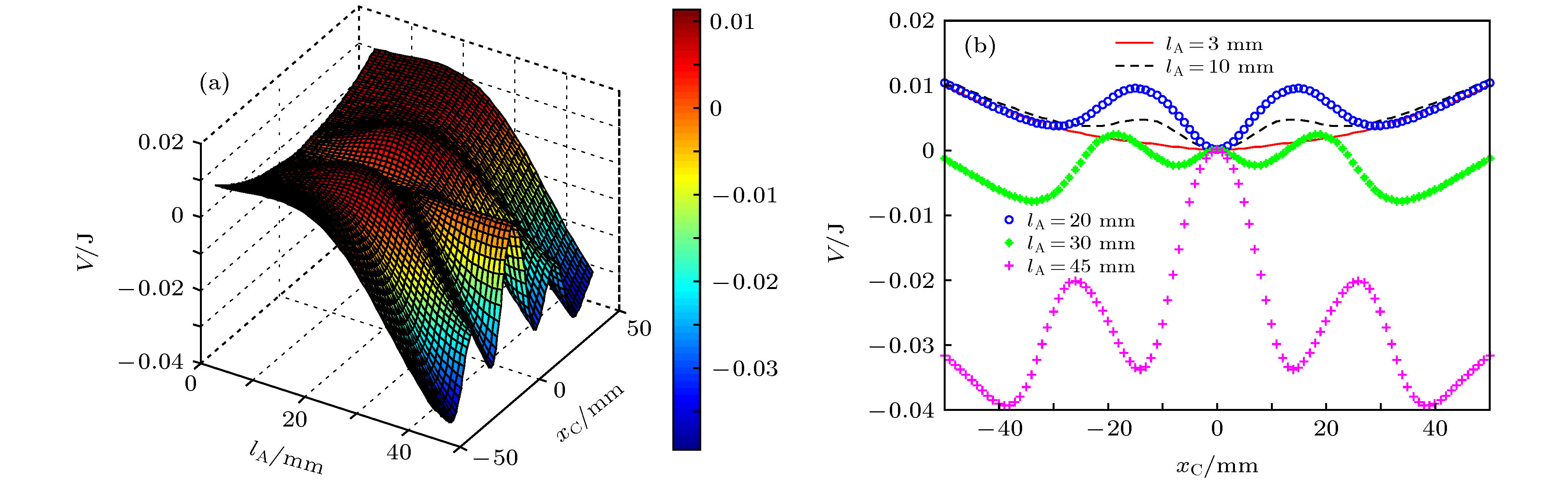
图 13 磁铁间距d = 6 mm, 不同矩形磁铁尺寸与环形磁铁(40 mm(φ1) × 20 mm(φ2) × 3 mm)作用的系统势函数 (a) 系统势函数三维图; (b) 矩形磁铁长度分别为lA = 3 mm, lA = 10 mm, lA = 20 mm, lA = 30 mm, lA = 45 mm时系统势函数二维图
Fig. 13. The system potential function varying with lA when d = 6 mm and the size of the ring magnet is 40 mm(φ1) × 20 mm(φ2) × 3 mm: (a) Three dimensional diagram of system potential function; (b) two dimensional diagram of system potential function when lA = 3 mm, lA = 10 mm, lA = 20 mm, lA = 30 mm and lA = 45 mm.
图 14 (a) lA = 20 mm和lA = 30 mm时, W2和W3随xC的变化关系;(b) lA = 20 mm和lA = 30 mm时, Fi随xC的变化
Fig. 14. (a) The curves of W2 and W3 varying with xC when lA = 20 mm and lA = 30 mm; (b) the curves of Fi varying with xC when lA = 20 mm and lA = 30 mm.
图 15 三稳结构 (a)中稳态点; (b)上稳态点
Fig. 15. The structure concluding three stable points: (a) The middle state point; (b) the upper stable point.
图 16 四稳结构 (a)上1稳态点; (b)上2稳态点
Fig. 16. The structure concluding four stable points: (a) The upper stable point 1; (b) the upper state point 2.
图 17 三稳振动响应 (a)时域图; (b)相位图
Fig. 17. The vibration response of the tri-stable cantilever beam: (a) The time domain chart; (b) the phase chart.
图 18 四稳振动响应 (a)时域图; (b)相位图
Fig. 18. The vibration response of the quad-stable cantilever beam: (a) The time domain chart; (b) the phase chart.
表 1 悬臂梁、矩形磁铁、环形磁铁的材料和参数
Table 1. Materials and parameters of cantilever beam, rectangular magnet, and ring magnet.
材料 参数 数值 悬臂梁材料: 矽钢 弹性模量EC/GPa 200 密度ρC/kg·m–3 7700 长度lC/mm 60 宽度wC/mm 10 厚度tC/mm 0.15 矩形磁铁材料:
Nd2Fe14B (牌号N35)密度ρA/kg·m–3 7500 长度lA/mm 10 宽度wA/mm 10 厚度tA/mm 3 磁化强度MA/A·m–1 6 × 105 环形磁铁材料:
Nd2Fe14B (牌号N35)密度ρB/kg·m–3 7500 厚度tB/mm 3 外环直径φ1/mm 40 内环直径φ2/mm 20 磁化强度MB/A·m–1 6 × 105 真空磁导率μ0/N·A–2 4π × 10–7 
下载: 导出CSV
表 2 实验器材及其型号
Table 2. Experimental equipments and models.
实验器材 型号 高斯计 BST100 推拉式测力计 HF-5 激光位移传感器 LK-G5001V
下载: 导出CSV
-
[1] Daynes S, Weaver P M 2012 Smart Mater. Struct. 21 105019
Google Scholar
[2] Barbarino S, Bilgen O, Ajaj R M, Friswell M I, Inman D J 2011 J. Intel. Mat. Syst. Str. 22 823
Google Scholar
[3] 姜伟红 2018 硕士学位论文(哈尔滨: 哈尔滨工业大学)
Jiang W H 2018 M. S. Thesis (Harbin: Harbin Institute of Technology) (in Chinese)
[4] Diaconu C G, Weaver P M, Mattioni F 2008 Thin Wall. Struct. 46 689
Google Scholar
[5] Daynes S, Nall S J, Weaver P M, Potter K D, Margaris P, Mellor P H 2010 J. Aircraft 47 334
Google Scholar
[6] 沙山克·普利亚, 丹尼尔·茵曼(黄见秋, 黄庆安, 译) 2010 能量收集技术 (南京: 东南大学出版社) 第 1—4 页
Priya S, Inman D J (Translated by Huang J Q, Huang Q A) 2010 Energy Harvesting Technologies (Nanjing: Southeast University Press) pp1–4 (in Chinese)
[7] 卢有为, 单小彪, 袁江波, 谢涛 2010 机械设计与制造 5 118
Google Scholar
Lu Y W, Shan X B, Yuan J B, Xie T 2010 Machinery Design & Manufacture 5 118
Google Scholar
[8] 王治平, 刘俊标, 姜楠, 李博 2010 压电与声光 32 763
Wang Z P, Liu J B, Jiang N, Li B 2010 Piezoelectrics & Acoustooptics 32 763
[9] Challa V R, Prasad M G, Fisher F T 2009 Smart Mater. Struct. 18 095029
Google Scholar
[10] 陈仲生, 杨拥民 2011 60 074301
Google Scholar
Chen Z S, Yang Y M 2011 Acta Phys. Sin. 60 074301
Google Scholar
[11] Podder P, Amann A, Roy S 2015 Sensor Actuat. A-Phys. 227 39
Google Scholar
[12] Gao Y J, Leng Y G, Fan S B, Lai Z H 2014 Smart Mater. Struct. 23 095003
Google Scholar
[13] Leng Y G, Tan D, Liu J J, Zhang Y Y, Fan S B 2017 J. Sound Vib. 406 146
Google Scholar
[14] Zhou S X, Cao J Y, Inman D J, Lin J, Liu S S, Wang Z Z 2014 Appl. Energy 133 33
Google Scholar
[15] Deng W, Wang Y 2017 Mech. Syst. Signal Pr. 85 591
Google Scholar
[16] Roundy S, Wright P K, Rabaey J 2003 Comput. Commun. 26 1131
Google Scholar
[17] DuToit N E, Wardle B L 2005 Integr. Ferroelectri. 45 1126
[18] Roundy S, Wright P K 2004 Smart Mater. Struct. 13 1131
Google Scholar
[19] Agashe J S, Arnold D P 2008 J. Phys. D: Appl. Phys. 41 105001
Google Scholar
[20] 张雨阳, 冷永刚, 谭丹, 刘进军, 范胜波 2017 66 220502
Google Scholar
Zhang Y Y, Leng Y G, Tan D, Liu J J, Fan S B 2017 Acta Phys. Sin. 66 220502
Google Scholar
[21] 谭丹, 冷永刚, 范胜波, 高毓璣 2015 64 060502
Google Scholar
Tan D, Leng Y G, Fan S B, Gao Y J 2015 Acta Phys. Sin. 64 060502
Google Scholar
[22] Tan D, Leng Y G, Gao Y J 2015 Eur. Phys. J.: Spec. Top. 224 2839
Google Scholar
下载:
计量
- 文章访问数: 8417
- PDF下载量: 174
- 被引次数: 0
