非晶态物质原子局域连接度与弛豫动力学

武振伟; 汪卫华

doi:10.7498/aps.69.20191870

摘要

非晶态物质的本质及形成过程是凝聚态物理领域最困难也是最有趣的问题之一. 非晶形成过程在原子结构上不会衍生出人们在传统晶体结构里所熟悉的长程有序性, 因此对于此类在自然界中广泛存在的物质形态, 至今还没有有效的实验表征手段和理论研究方法. 非晶态物质的原子结构及其构效关系的研究是凝聚态物理和材料科学等众多研究领域所关注的热点问题之一. 随着对非晶态物质物性研究的深入, 人们逐渐意识到非晶态物质中原子中程序对系统性质的重要影响, 建立以中程序为基础的结构-动力学关系对于理解玻璃及玻璃转变的本质起着重要的作用. 本文简要综述了基于图论提出的原子局域连接度这一新的结构序参量在液体和玻璃的结构及构效关系研究中的应用. 新的结构序参量从过去侧重于关注局域原子团簇的种类和分布, 转移到更加关注某一类具有特殊对称性的原子的空间连接情况, 即更多地尝试从原子中程序的角度来建立非晶态物质中的构效关系. 新的研究结果表明, 局域连接度可与非晶态物质中原子的短时或长时动力学行为、输运方式、以及振动模态等一系列物理性质建立联系.

关键词:

Abstract

For a long time, it has been well recognized that there exists a deep link between the fast vibrational excitations and the slow diffusive dynamics in glass-forming systems. However, it remains as an open question whether and how the short-time scale dynamics associated with vibrational intrabasin excitations is related to the long-time dynamics associated with diffusive interbasin hoppings. In this paper we briefly review the research progress that addresses this challenge. By identifying a structural order parameter—local connectivity of a particle which is defined as the number of nearest neighbors having the same local spatial symmetry, it is found that the local connectivity can tune and modulate both the short-time vibrational dynamics and the long-time relaxation dynamics of the studied particles in a model of metallic supercooled liquid. Furthermore, it reveals that the local connectivity leads the long-time decay of the correlation functions to change from stretched exponentials to compressed ones, indicating a dynamic crossover from diffusive to hyperdiffusive motions. This is the first time to report that in supercooled liquids the particles with particular spatial symmetry can present a faster-than-exponential relaxation that has so far only been reported in out-of-equilibrium materials. The recent results suggest a structural bridge to link the fast vibrational dynamics to the slow structural relaxation in glass-forming systems and extends the compressed exponential relaxation phenomenon from earlier reported out-of-equilibrium materials to the metastable supercooled liquids.

Keywords:

作者及机构信息

武振伟¹,
汪卫华²

1.
北京师范大学系统科学学院, 北京　100875

2.
中国科学院物理研究所, 北京　100190

通信作者: 武振伟, zwwu@bnu.edu.cn

Authors and contacts

Wu Zhen-Wei¹,
Wang Wei-Hua²

1.
School of Systems Science, Beijing Normal University, Beijing 100875, China

2.
Institute of Physics, Chinese Academy of Sciences, Beijing 100190, China

Corresponding author: Wu Zhen-Wei, zwwu@bnu.edu.cn

文章全文 : translate this paragraph

参考文献

[1]	Wang W H 2013 Prog. Phys. 33 177
[2]	Wang W H 2019 Prog. Mater. Sci. 106 100561 Google Scholar
[3]	Li M X, Zhao S F, Lu Z, Hirata A, Wen P, Bai H Y, Chen M, Schroers J, Liu Y, Wang W H 2019 Nature 569 99 Google Scholar
[4]	Anderson P W 1995 Science 267 1611 Google Scholar
[5]	Debenedetti P G, Stillinger F H 2001 Nature 410 259 Google Scholar
[6]	Cheng Y Q, Ma E 2011 Prog. Mater. Sci. 56 379 Google Scholar
[7]	李茂枝 2017 66 176107 Google Scholar Li M Z 2017 Acta Phys. Sin. 66 176107 Google Scholar
[8]	管鹏飞, 王兵, 吴义成, 张珊, 尚宝双, 胡远超, 苏锐, 刘琪 2017 66 176112 Google Scholar Guan P F, Wang B, Wu Y C, Zhang S, Shang B S, Hu Y C, Su R, Liu Q 2017 Acta Phys. Sin. 66 176112 Google Scholar
[9]	Yang X, Liu R, Yang M, Wang W H, Chen K 2016 Phys. Rev. Lett. 116 238003 Google Scholar
[10]	Schoenholz S S, Cubuk E D, Sussman D M, Kaxiras E, Liu A J 2016 Nat. Phys. 12 469 Google Scholar
[11]	Tong H, Xu N 2014 Phys. Rev. E 90 010401 Google Scholar
[12]	Ning L, Liu P, Zong Y, Liu R, Yang M, Chen K 2019 Phys. Rev. Lett. 122 178002 Google Scholar
[13]	Li M, Wang C Z, Hao S G, Kramer M J, Ho K M 2009 Phys. Rev. B 80 184201 Google Scholar
[14]	Ma D, Stoica A D, Wang X L 2009 Nat. Mater. 8 30 Google Scholar
[15]	Liu X J, Xu Y, Hui X, Lu Z P, Li F, Chen G L, Lu J, Liu C T 2010 Phys. Rev. Lett. 105 155501 Google Scholar
[16]	Zeng Q, Sheng H, Ding Y, Wang L, Yang W, Jiang J Z, Mao W L, Mao H K 2011 Science 332 1404 Google Scholar
[17]	Lü Y J, Entel P 2011 Phys. Rev. B 84 104203 Google Scholar
[18]	Wu Z W, Li M Z, Wang W H, Liu K X 2015 Nat. Commun. 6 6035 Google Scholar
[19]	Pan S, Wu Z W, Wang W H, Li M Z, Xu L 2017 Sci. Rep. 7 39938 Google Scholar
[20]	武振伟, 李茂枝, 徐莉梅, 汪卫华 2017 66 176405 Google Scholar Wu Z W, Li M Z, Xu L M, Wang W H 2017 Acta Phys. Sin. 66 176405 Google Scholar
[21]	Liu X J, Wang S D, Wang H, Wu Y, Liu C T, Li M, Lu Z P 2018 Phys. Rev. B 97 134107 Google Scholar
[22]	Li F X, Kong J B, Li M Z 2018 Chin. Phys. B 27 056102 Google Scholar
[23]	Topological phase transition and topological phases of matter, the Royal Swedish Academy of Sciences https://www.nobel prize.org/uploads/2018/06/advanced-physicsprize2016.pdf [2019-12-10]
[24]	Cao Y, Li J, Kou B, Xia C, Li Z, Chen R, Xie H, Xiao T, Kob W, Hong L, Zhang J, Wang Y 2018 Nat. Commun. 9 2911 Google Scholar
[25]	Peng H L, Li M Z, Wang W H, Wang C -Z, Ho K M 2010 Appl. Phys. Lett. 96 021901 Google Scholar
[26]	Peng H L, Li M Z, Wang W H 2011 Phys. Rev. Lett. 106 135503 Google Scholar
[27]	Li M Z 2014 J. Mater. Sci. Technol. 30 551 Google Scholar
[28]	Hu Y C, Li F X, Li M Z, Bai H Y, Wang W H 2015 Nat. Commun. 6 8310 Google Scholar
[29]	Li F X, Li M Z 2017 J. Appl. Phys. 122 225103 Google Scholar
[30]	Wu Z W, Li M Z, Wang W H, Liu K X 2013 Phys. Rev. B 88 054202 Google Scholar
[31]	Wu Z W, Li F X, Huo C W, Li M Z, Wang W H, Liu K X 2016 Sci. Rep. 6 35967 Google Scholar
[32]	Wu Z W, Li M Z, Wang W H, Song W J, Liu K X 2013 J. Chem. Phys. 138 074502 Google Scholar
[33]	Jiang S Q, Wu Z W, Li M Z 2016 J. Chem. Phys. 144 154502 Google Scholar
[34]	Zhang H P, Wang F R, Li M Z 2019 J. Phys. Chem. B 123 1149 Google Scholar
[35]	Xu L, Kumar P, Buldyrev S V, Chen S H, Poole P H, Sciortino F, Stanley H E 2005 Proc. Natl. Acad. Sci. 102 16558 Google Scholar
[36]	Xu L, Buldyrev S V, Angell C A, Stanley H E 2006 Phys. Rev. E 74 31108 Google Scholar
[37]	李任重, 武振伟, 徐莉梅 2017 66 176410 Google Scholar Li R Z, Wu Z W, Xu L M 2017 Acta Phys. Sin. 66 176410 Google Scholar
[38]	孙保安, 王利峰, 邵建华 2017 66 178103 Google Scholar Sun B A, Wang L F, Shao J H 2017 Acta Phys. Sin. 66 178103 Google Scholar
[39]	王峥, 汪卫华 2017 66 176103 Google Scholar Wang Z, Wang W H 2017 Acta Phys. Sin. 66 176103 Google Scholar
[40]	袁晨晨 2017 66 176402 Google Scholar Yuan C C 2017 Acta Phys. Sin. 66 176402 Google Scholar
[41]	Lad K N, Jakse N, Pasturel A 2017 J. Chem. Phys. 146 124502 Google Scholar
[42]	Mendelev M I, Sordelet D J, Kramer M J 2007 J. Appl. Phys. 102 043501 Google Scholar
[43]	Plimpton S 1995 J. Comput. Phys. 117 1 Google Scholar
[44]	Newman M E J 2003 SIAM Review 45 167 Google Scholar
[45]	Kob W, Andersen H C 1995 Phys. Rev. E 51 4626
[46]	Kob W, Andersen H C 1995 Phys. Rev. E 52 4134 Google Scholar
[47]	Yuan C C, Yang F, Kargl F, Holland-Moritz D, Simeoni G G, Meyer A 2015 Phys. Rev. B 91 214203
[48]	Francesco S 2005 J. Stat. Mech. 2005 P05015
[49]	Wu Z W, Kob W, Wang W H, Xu L 2018 Nat. Commun. 9 5334 Google Scholar
[50]	Zhang L, Zheng J, Wang Y, Zhang L, Jin Z, Hong L, Wang Y, Zhang J 2017 Nat. Commun. 8 67 Google Scholar
[51]	陈科 2017 66 178201 Google Scholar Chen K 2017 Acta Phys. Sin. 66 178201 Google Scholar
[52]	Yang J, Wang Y J, Ma E, Zaccone A, Dai L H, Jiang M Q 2019 Phys. Rev. Lett. 122 015501 Google Scholar
[53]	Wang L, Ninarello A, Guan P, Berthier L, Szamel G, Flenner E 2019 Nat. Commun. 10 26 Google Scholar
[54]	Ediger M D, Angell C A, Nagel S R 1996 J. Phys. Chem. 100 13200 Google Scholar
[55]	Kob W 1999 J. Phys: Condens. Matter 11 R85 Google Scholar
[56]	Ruta B, Baldi G, Chushkin Y, Rufflé B, Cristofolini L, Fontana A, Zanatta M, Nazzani F 2014 Nat. Commun. 5 3939 Google Scholar
[57]	Ruta B, Baldi G, Scarponi F, Fioretto D, Giordano V M, Monaco G 2012 J. Chem. Phys. 137 214502 Google Scholar
[58]	Cipelletti L, Manley S, Ball R C, Weitz D A 2000 Phys. Rev. Lett. 84 2275 Google Scholar
[59]	Ballesta P, Duri A, Cipelletti L 2008 Nat. Phys. 4 550 Google Scholar
[60]	Caronna C, Chushkin Y, Madsen A, Cupane A 2008 Phys. Rev. Lett. 100 055702 Google Scholar
[61]	Guo H, Bourret G, Corbierre M K, Rucareanu S, Lennox R B, Laaziri K, Piche L, Sutton M, Harden J L, Leheny R L 2009 Phys. Rev. Lett. 102 075702 Google Scholar
[62]	Angell C A 1995 Science 267 1924 Google Scholar
[63]	Horbach J, Kob W, Binder K, Angell C A 1996 Phys. Rev. E 54 R5897 Google Scholar
[64]	Kob W, Barrat J-L 1997 Phys. Rev. Lett. 78 4581 Google Scholar
[65]	Horbach J, Kob W, Binder K 2001 Eur. Phys. J. B 19 531 Google Scholar
[66]	Sastry S, Austen Angell C 2003 Nat. Mater. 2 739 Google Scholar
[67]	Sette F, Krisch M H, Masciovecchio C, Ruocco G, Monaco G 1998 Science 280 1550 Google Scholar
[68]	Sokolov A P, Rössler E, Kisliuk A, Quitmann D 1993 Phys. Rev. Lett. 71 2062 Google Scholar
[69]	Scopigno T, Ruocco G, Sette F, Monaco G 2003 Science 302 849 Google Scholar
[70]	Shintani H, Tanaka H 2008 Nat. Mater. 7 870 Google Scholar
[71]	Huang B, Zhu Z G, Ge T P, Bai H Y, Sun B A, Yang Y, Liu C T, Wang W H 2016 Acta Mater. 110 73 Google Scholar
[72]	Luo P, Li Y Z, Bai H Y, Wen P, Wang W H 2016 Phys. Rev. Lett. 116 175901 Google Scholar
[73]	Finney J L 1977 Nature 266 309 Google Scholar
[74]	Sheng H W, Luo W K, Alamgir F M, Bai J M, Ma E 2006 Nature 439 419 Google Scholar
[75]	Wakeda M, Shibutani Y 2010 Acta Mater 58 3963 Google Scholar
[76]	Hansen J, McDonald I 2006 Theory of Simple Liquids (3rd Ed.) (London; Burlingtong, MA: Elsevier Academic Press) p185
[77]	Binder K, Kob W 2011 Glassy Materials and Disordered Solids: An Introduction to Their Statistical Mechanics (Revised Edition) (Singapore: World Scientific) pp35−79
[78]	Zhang Y, Wang C Z, Zhang F, Mendelev M I, Kramer M J, Ho K M 2014 Appl. Phys. Lett. 105 061905 Google Scholar
[79]	Luo P, Wen P, Bai H Y, Ruta B, Wang W H 2017 Phys. Rev. Lett. 118 225901 Google Scholar
[80]	Desgranges C, Delhommelle J 2019 Phys. Rev. Lett. 123 195701 Google Scholar
[81]	Desgranges C, Delhommelle J 2018 Phys. Rev. Lett. 120 115701 Google Scholar
[82]	Bi Q L, Lü Y J, Wang W H 2018 Phys. Rev. Lett. 120 155501 Google Scholar

施引文献

图 1 静态结构因子S(q)的数值计算结果二维示意图 (a)无序结构; (b)有序晶体结构

Fig. 1. Structure factor S(q) obtained in computer simulation: (a) For disordered structure; (b) for ordered crystal structure.

下载: 全尺寸图片幻灯片

图 2 液态Cu₅₀Zr₅₀在1000 K下的静态结构因子S(q) (图中对不同计算方式得到的结果进行了对比)

Fig. 2. Structure factors S(q) of liquid Cu₅₀Zr₅₀ at 1000 K, obtained with different protocols.

下载: 全尺寸图片幻灯片

图 3 图或网络的示例以及它的邻接矩阵^[44]

Fig. 3. A small example graph (or network) with its adjacency matrix^[44].

下载: 全尺寸图片幻灯片

图 4 CuZr合金中Cu原子和Zr原子在1000 K下的均方位移

Fig. 4. Mean-square displacement for Cu/Zr atoms in liquid CuZr alloy at 1000 K.

下载: 全尺寸图片幻灯片

图 5 相干散射函数F(q, t)和自散射函数F_s(q, t)在不同q下的比较　(a) q = 0.6 Å^－1; (b) q = 2.8 Å^－1

Fig. 5. Comparison between F(q, t) and F_s(q, t) at different q values: (a) q = 0.6 Å^－1; (b) q = 2.8 Å^－1.

下载: 全尺寸图片幻灯片

图 6 针对CuZr玻璃的不同粒子数及不同计算方法所获得的振动态密度D(ω)的比较, 及对玻色峰的展示^[49]

Fig. 6. Vibrational density of states for CuZr glass with different protocols, and the test for the present of a boson peak^[49].

下载: 全尺寸图片幻灯片

图 7 CuZr金属玻璃10 K下通过对其原子的速度自关联函数进行傅里叶变换所得到的振动态密度, 数据表明10 K下系统内部已经几乎不存在可能影响到D(ω)的老化过程

Fig. 7. Vibrational density of states obtained by calculation of the time Fourier transformation of the velocity auto-correlation function. It can be seen that there is no apparent aging effect at 10 K.

下载: 全尺寸图片幻灯片

图 8 局域连接度定义的示意图(指定原子的最近邻原子中, 与指定原子具有相同局域对称性(用相同的颜色表示)的原子的总数即为指定原子的连接度)

Fig. 8. Illustration of the definition of particles with different connectivities k : Particles in blue are the center of an icosahedral-like cluster.

下载: 全尺寸图片幻灯片

图 9 不同温度下二十面体中心原子的连接度的分布^[49] (a) T = 1100 K; (b) T = 1000 K; (c) T = 950 K

Fig. 9. Probability that an icosahedron is of type k^[49]: (a) T = 1100 K; (b) T = 1000 K; (c) T = 950 K.

下载: 全尺寸图片幻灯片

图 10 Cu₅₀Zr₅₀在不同温度下的静态结构因子S(q)^[49]

Fig. 10. The q-dependence of the partial structure factors for three temperatures considered^[49].

下载: 全尺寸图片幻灯片

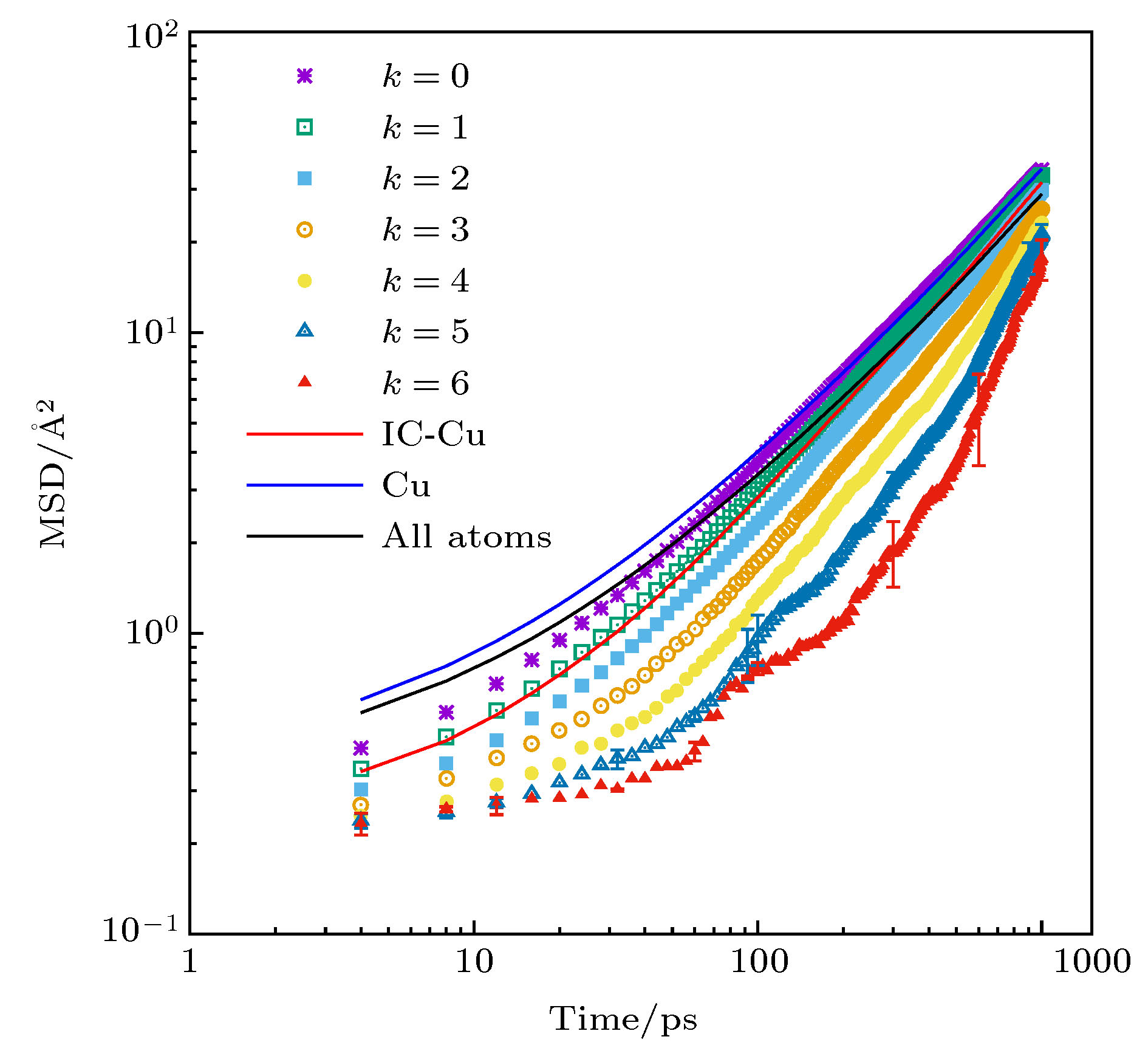
图 11 具有不同k值的粒子的自散射函数(SISF)^[49], 图中黑色实线为唯象模型((9)式)的拟合结果, 图的右上角给出SISF曲线的整体形状; 其他类型粒子的SISF曲线也一并在图中给出, 以方便对比

Fig. 11. Short-time behavior of the self-intermediate scattering function of particles with different local connectivity k (symbols)^[49]. The wave-vector is q = 2.8 Å^–1 and T = 1000 K. The solid lines are fits to the data with Eq. (9). Also included is F_s(q, t) for the Cu atoms in an icosahedral cluster (dashed red line), the Cu atoms not in an icosahedral cluster (blue dashed line), and all Cu atoms (green). The black dashed line is the correlation function averaged over all atoms. The upper inset shows the same data in a larger time interval.

下载: 全尺寸图片幻灯片

图 12 具有不同k值原子的振动态密度D(ω)

Fig. 12. Vibrational density of states of particles with different local connectivity k.

下载: 全尺寸图片幻灯片

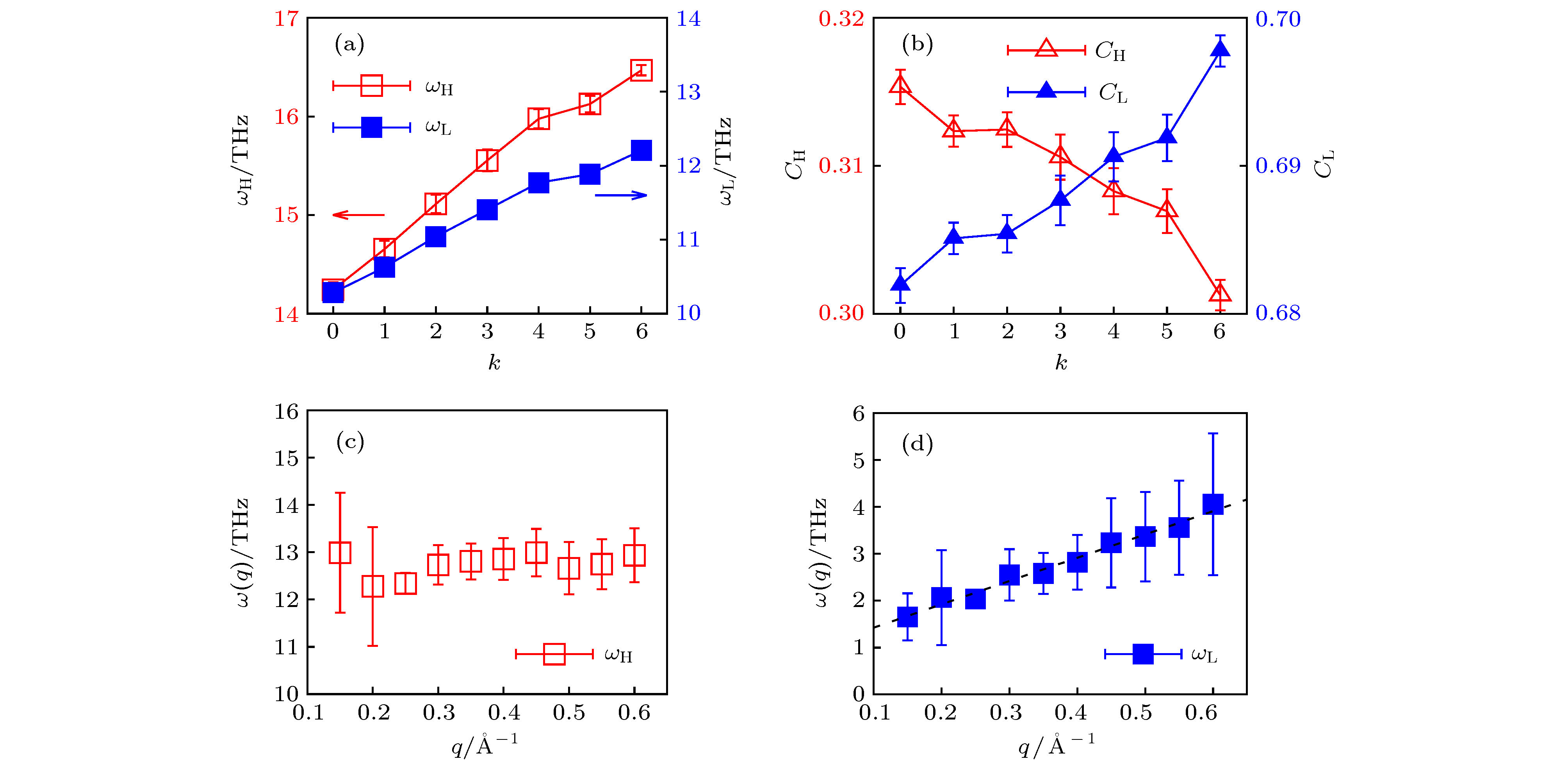
图 13 (a) ω_H和ω_L与局域连接度k均成正相关关系^[49]; (b) 随着k值的增加, 权重因子C_L上升而C_H降低; (c) 高频模式ω_H(q)的波矢q无关性表明其局域模式的特征; (d) ω_L(q)所具有的色散关系表明它是一种扩展性质的模式, 图中黑色虚线为相应数据点的线性拟合

Fig. 13. (a) Both the high and low frequency modes, ω_H and ω_L, increases with increasing k^[49]; (b) the fraction of motion C_L/H increases for ω_L and decreases for ω_H; (c) the high frequency mode ω_H(q) is approximately q-independent, characteristic of localization of the vibrational modes; (d) the low frequency mode ω_L(q) increases monotonically with increasing q, characteristic of collective dynamics.

下载: 全尺寸图片幻灯片

图 14 (a) 具有不同k值的粒子在q = 2.8 Å^–1下的长时动力学弛豫曲线, 图中黑色实线为KWW公式拟合所得^[49]; (b) 不同波矢q下的形状因子β与k值的关系, β值的变化预示着动力学行为从拉伸e指数弛豫到压缩e指数形式的转变, 转变的有无及具体位置与波矢q密切相关

Fig. 14. (a) Long-time decay of the correlation functions at q = 2.8 Å^–1 for particles with different k values^[49]. The black solid lines are the Kohlrausch-Williams-Watt (KWW) fits. (b) The k dependence of the exponent β. The variation of β reveals a dynamic crossover from stretched (β < 1) exponential relaxation to compressed (β > 1) one. It can be seen that the cross-over from stretched to compressed exponential depends on q.

下载: 全尺寸图片幻灯片

图 15 弛豫时间τ与波矢q之间的关系, 为了更好地区分1/q scaling和1/q² scaling, 这里把数据重新表述成了qτ与q之间的关系^[49]

Fig. 15. Wave vector q dependence of the relaxation time τ of the final decay of F_s(q, t) for particles having different local connectivities^[49]. Here we show qτ as a function of q to make it simpler to see the 1/q law and to distinguish it from the 1/q² law.

下载: 全尺寸图片幻灯片

图 16 1000 K下标记为不同类型的原子的均方位移曲线^[49]

Fig. 16. Mean squared displacement for different type of atoms at 1000 K^[49]

下载: 全尺寸图片幻灯片

map

[1]	Wang W H 2013 Prog. Phys. 33 177
[2]	Wang W H 2019 Prog. Mater. Sci. 106 100561 Google Scholar
[3]	Li M X, Zhao S F, Lu Z, Hirata A, Wen P, Bai H Y, Chen M, Schroers J, Liu Y, Wang W H 2019 Nature 569 99 Google Scholar
[4]	Anderson P W 1995 Science 267 1611 Google Scholar
[5]	Debenedetti P G, Stillinger F H 2001 Nature 410 259 Google Scholar
[6]	Cheng Y Q, Ma E 2011 Prog. Mater. Sci. 56 379 Google Scholar
[7]	李茂枝 2017 66 176107 Google Scholar Li M Z 2017 Acta Phys. Sin. 66 176107 Google Scholar
[8]	管鹏飞, 王兵, 吴义成, 张珊, 尚宝双, 胡远超, 苏锐, 刘琪 2017 66 176112 Google Scholar Guan P F, Wang B, Wu Y C, Zhang S, Shang B S, Hu Y C, Su R, Liu Q 2017 Acta Phys. Sin. 66 176112 Google Scholar
[9]	Yang X, Liu R, Yang M, Wang W H, Chen K 2016 Phys. Rev. Lett. 116 238003 Google Scholar
[10]	Schoenholz S S, Cubuk E D, Sussman D M, Kaxiras E, Liu A J 2016 Nat. Phys. 12 469 Google Scholar
[11]	Tong H, Xu N 2014 Phys. Rev. E 90 010401 Google Scholar
[12]	Ning L, Liu P, Zong Y, Liu R, Yang M, Chen K 2019 Phys. Rev. Lett. 122 178002 Google Scholar
[13]	Li M, Wang C Z, Hao S G, Kramer M J, Ho K M 2009 Phys. Rev. B 80 184201 Google Scholar
[14]	Ma D, Stoica A D, Wang X L 2009 Nat. Mater. 8 30 Google Scholar
[15]	Liu X J, Xu Y, Hui X, Lu Z P, Li F, Chen G L, Lu J, Liu C T 2010 Phys. Rev. Lett. 105 155501 Google Scholar
[16]	Zeng Q, Sheng H, Ding Y, Wang L, Yang W, Jiang J Z, Mao W L, Mao H K 2011 Science 332 1404 Google Scholar
[17]	Lü Y J, Entel P 2011 Phys. Rev. B 84 104203 Google Scholar
[18]	Wu Z W, Li M Z, Wang W H, Liu K X 2015 Nat. Commun. 6 6035 Google Scholar
[19]	Pan S, Wu Z W, Wang W H, Li M Z, Xu L 2017 Sci. Rep. 7 39938 Google Scholar
[20]	武振伟, 李茂枝, 徐莉梅, 汪卫华 2017 66 176405 Google Scholar Wu Z W, Li M Z, Xu L M, Wang W H 2017 Acta Phys. Sin. 66 176405 Google Scholar
[21]	Liu X J, Wang S D, Wang H, Wu Y, Liu C T, Li M, Lu Z P 2018 Phys. Rev. B 97 134107 Google Scholar
[22]	Li F X, Kong J B, Li M Z 2018 Chin. Phys. B 27 056102 Google Scholar
[23]	Topological phase transition and topological phases of matter, the Royal Swedish Academy of Sciences https://www.nobel prize.org/uploads/2018/06/advanced-physicsprize2016.pdf [2019-12-10]
[24]	Cao Y, Li J, Kou B, Xia C, Li Z, Chen R, Xie H, Xiao T, Kob W, Hong L, Zhang J, Wang Y 2018 Nat. Commun. 9 2911 Google Scholar
[25]	Peng H L, Li M Z, Wang W H, Wang C -Z, Ho K M 2010 Appl. Phys. Lett. 96 021901 Google Scholar
[26]	Peng H L, Li M Z, Wang W H 2011 Phys. Rev. Lett. 106 135503 Google Scholar
[27]	Li M Z 2014 J. Mater. Sci. Technol. 30 551 Google Scholar
[28]	Hu Y C, Li F X, Li M Z, Bai H Y, Wang W H 2015 Nat. Commun. 6 8310 Google Scholar
[29]	Li F X, Li M Z 2017 J. Appl. Phys. 122 225103 Google Scholar
[30]	Wu Z W, Li M Z, Wang W H, Liu K X 2013 Phys. Rev. B 88 054202 Google Scholar
[31]	Wu Z W, Li F X, Huo C W, Li M Z, Wang W H, Liu K X 2016 Sci. Rep. 6 35967 Google Scholar
[32]	Wu Z W, Li M Z, Wang W H, Song W J, Liu K X 2013 J. Chem. Phys. 138 074502 Google Scholar
[33]	Jiang S Q, Wu Z W, Li M Z 2016 J. Chem. Phys. 144 154502 Google Scholar
[34]	Zhang H P, Wang F R, Li M Z 2019 J. Phys. Chem. B 123 1149 Google Scholar
[35]	Xu L, Kumar P, Buldyrev S V, Chen S H, Poole P H, Sciortino F, Stanley H E 2005 Proc. Natl. Acad. Sci. 102 16558 Google Scholar
[36]	Xu L, Buldyrev S V, Angell C A, Stanley H E 2006 Phys. Rev. E 74 31108 Google Scholar
[37]	李任重, 武振伟, 徐莉梅 2017 66 176410 Google Scholar Li R Z, Wu Z W, Xu L M 2017 Acta Phys. Sin. 66 176410 Google Scholar
[38]	孙保安, 王利峰, 邵建华 2017 66 178103 Google Scholar Sun B A, Wang L F, Shao J H 2017 Acta Phys. Sin. 66 178103 Google Scholar
[39]	王峥, 汪卫华 2017 66 176103 Google Scholar Wang Z, Wang W H 2017 Acta Phys. Sin. 66 176103 Google Scholar
[40]	袁晨晨 2017 66 176402 Google Scholar Yuan C C 2017 Acta Phys. Sin. 66 176402 Google Scholar
[41]	Lad K N, Jakse N, Pasturel A 2017 J. Chem. Phys. 146 124502 Google Scholar
[42]	Mendelev M I, Sordelet D J, Kramer M J 2007 J. Appl. Phys. 102 043501 Google Scholar
[43]	Plimpton S 1995 J. Comput. Phys. 117 1 Google Scholar
[44]	Newman M E J 2003 SIAM Review 45 167 Google Scholar
[45]	Kob W, Andersen H C 1995 Phys. Rev. E 51 4626
[46]	Kob W, Andersen H C 1995 Phys. Rev. E 52 4134 Google Scholar
[47]	Yuan C C, Yang F, Kargl F, Holland-Moritz D, Simeoni G G, Meyer A 2015 Phys. Rev. B 91 214203
[48]	Francesco S 2005 J. Stat. Mech. 2005 P05015
[49]	Wu Z W, Kob W, Wang W H, Xu L 2018 Nat. Commun. 9 5334 Google Scholar
[50]	Zhang L, Zheng J, Wang Y, Zhang L, Jin Z, Hong L, Wang Y, Zhang J 2017 Nat. Commun. 8 67 Google Scholar
[51]	陈科 2017 66 178201 Google Scholar Chen K 2017 Acta Phys. Sin. 66 178201 Google Scholar
[52]	Yang J, Wang Y J, Ma E, Zaccone A, Dai L H, Jiang M Q 2019 Phys. Rev. Lett. 122 015501 Google Scholar
[53]	Wang L, Ninarello A, Guan P, Berthier L, Szamel G, Flenner E 2019 Nat. Commun. 10 26 Google Scholar
[54]	Ediger M D, Angell C A, Nagel S R 1996 J. Phys. Chem. 100 13200 Google Scholar
[55]	Kob W 1999 J. Phys: Condens. Matter 11 R85 Google Scholar
[56]	Ruta B, Baldi G, Chushkin Y, Rufflé B, Cristofolini L, Fontana A, Zanatta M, Nazzani F 2014 Nat. Commun. 5 3939 Google Scholar
[57]	Ruta B, Baldi G, Scarponi F, Fioretto D, Giordano V M, Monaco G 2012 J. Chem. Phys. 137 214502 Google Scholar
[58]	Cipelletti L, Manley S, Ball R C, Weitz D A 2000 Phys. Rev. Lett. 84 2275 Google Scholar
[59]	Ballesta P, Duri A, Cipelletti L 2008 Nat. Phys. 4 550 Google Scholar
[60]	Caronna C, Chushkin Y, Madsen A, Cupane A 2008 Phys. Rev. Lett. 100 055702 Google Scholar
[61]	Guo H, Bourret G, Corbierre M K, Rucareanu S, Lennox R B, Laaziri K, Piche L, Sutton M, Harden J L, Leheny R L 2009 Phys. Rev. Lett. 102 075702 Google Scholar
[62]	Angell C A 1995 Science 267 1924 Google Scholar
[63]	Horbach J, Kob W, Binder K, Angell C A 1996 Phys. Rev. E 54 R5897 Google Scholar
[64]	Kob W, Barrat J-L 1997 Phys. Rev. Lett. 78 4581 Google Scholar
[65]	Horbach J, Kob W, Binder K 2001 Eur. Phys. J. B 19 531 Google Scholar
[66]	Sastry S, Austen Angell C 2003 Nat. Mater. 2 739 Google Scholar
[67]	Sette F, Krisch M H, Masciovecchio C, Ruocco G, Monaco G 1998 Science 280 1550 Google Scholar
[68]	Sokolov A P, Rössler E, Kisliuk A, Quitmann D 1993 Phys. Rev. Lett. 71 2062 Google Scholar
[69]	Scopigno T, Ruocco G, Sette F, Monaco G 2003 Science 302 849 Google Scholar
[70]	Shintani H, Tanaka H 2008 Nat. Mater. 7 870 Google Scholar
[71]	Huang B, Zhu Z G, Ge T P, Bai H Y, Sun B A, Yang Y, Liu C T, Wang W H 2016 Acta Mater. 110 73 Google Scholar
[72]	Luo P, Li Y Z, Bai H Y, Wen P, Wang W H 2016 Phys. Rev. Lett. 116 175901 Google Scholar
[73]	Finney J L 1977 Nature 266 309 Google Scholar
[74]	Sheng H W, Luo W K, Alamgir F M, Bai J M, Ma E 2006 Nature 439 419 Google Scholar
[75]	Wakeda M, Shibutani Y 2010 Acta Mater 58 3963 Google Scholar
[76]	Hansen J, McDonald I 2006 Theory of Simple Liquids (3rd Ed.) (London; Burlingtong, MA: Elsevier Academic Press) p185
[77]	Binder K, Kob W 2011 Glassy Materials and Disordered Solids: An Introduction to Their Statistical Mechanics (Revised Edition) (Singapore: World Scientific) pp35−79
[78]	Zhang Y, Wang C Z, Zhang F, Mendelev M I, Kramer M J, Ho K M 2014 Appl. Phys. Lett. 105 061905 Google Scholar
[79]	Luo P, Wen P, Bai H Y, Ruta B, Wang W H 2017 Phys. Rev. Lett. 118 225901 Google Scholar
[80]	Desgranges C, Delhommelle J 2019 Phys. Rev. Lett. 123 195701 Google Scholar
[81]	Desgranges C, Delhommelle J 2018 Phys. Rev. Lett. 120 115701 Google Scholar
[82]	Bi Q L, Lü Y J, Wang W H 2018 Phys. Rev. Lett. 120 155501 Google Scholar

[1]	张剑, 郝奇, 张浪渟, 乔吉超. 不同力学激励形式探索La基非晶合金微观结构非均匀性. , 2024, 73(4): 046101. doi: 10.7498/aps.73.20231421
[2]	孟绍怡, 郝奇, 王兵, 段亚娟, 乔吉超. 冷却速率对La基非晶合金β弛豫行为和应力弛豫的影响. , 2024, 73(3): 036101. doi: 10.7498/aps.73.20231417
[3]	黄蓓蓓, 郝奇, 吕国建, 乔吉超. 锆基非晶合金的动态弛豫和应力松弛. , 2023, 72(13): 136101. doi: 10.7498/aps.72.20230181
[4]	孟绍怡, 郝奇, 吕国建, 乔吉超. La基非晶合金β弛豫行为: 退火和加载应变的影响. , 2023, 72(7): 076101. doi: 10.7498/aps.72.20222389
[5]	周边, 杨亮. 分子动力学模拟冷却速率对非晶合金结构与变形行为的影响. , 2020, 69(11): 116101. doi: 10.7498/aps.69.20191781
[6]	文大东, 邓永和, 戴雄英, 吴安如, 田泽安. 钽过冷液体等温晶化的原子层面机制. , 2020, 69(19): 196101. doi: 10.7498/aps.69.20200665
[7]	冯涛, Horst Hahn, Herbert Gleiter. 纳米结构非晶合金材料研究进展. , 2017, 66(17): 176110. doi: 10.7498/aps.66.176110
[8]	柳延辉. 非晶合金的高通量制备与表征. , 2017, 66(17): 176106. doi: 10.7498/aps.66.176106
[9]	柯海波, 蒲朕, 张培, 张鹏国, 徐宏扬, 黄火根, 刘天伟, 王英敏. 铀基非晶合金的发展现状. , 2017, 66(17): 176104. doi: 10.7498/aps.66.176104
[10]	平志海, 钟鸣, 龙志林. 基于逾渗理论的非晶合金屈服行为研究. , 2017, 66(18): 186101. doi: 10.7498/aps.66.186101
[11]	王峥, 汪卫华. 非晶合金中的流变单元. , 2017, 66(17): 176103. doi: 10.7498/aps.66.176103
[12]	卞西磊, 王刚. 非晶合金的离子辐照效应. , 2017, 66(17): 178101. doi: 10.7498/aps.66.178101
[13]	孙川琴, 黄海深, 毕庆玲, 吕勇军. 非晶态合金表面的水润湿动力学. , 2017, 66(17): 176101. doi: 10.7498/aps.66.176101
[14]	李茂枝. 非晶合金及合金液体的局域五次对称性. , 2017, 66(17): 176107. doi: 10.7498/aps.66.176107
[15]	刘丽霞, 侯兆阳, 刘让苏. 过冷液体钾形核初期微观动力学机理的模拟研究. , 2012, 61(5): 056101. doi: 10.7498/aps.61.056101
[16]	赵兴宇, 王丽娜, 樊小辉, 张丽丽, 卫来, 张晋鲁, 黄以能. 玻璃化转变的分子串模型中分子串弛豫模式的计算机模拟. , 2011, 60(3): 036403. doi: 10.7498/aps.60.036403
[17]	樊小辉, 赵兴宇, 王丽娜, 张丽丽, 周恒为, 张晋鲁, 黄以能. 分子串模型中空间弛豫模式的弛豫动力学的蒙特卡罗模拟. , 2011, 60(12): 126401. doi: 10.7498/aps.60.126401
[18]	闫志杰, 李金富, 周尧和, 仵彦卿. 压痕塑性变形诱导非晶合金的晶化. , 2007, 56(2): 999-1003. doi: 10.7498/aps.56.999
[19]	程伟东, 孙民华, 李佳云, 王爱屏, 孙永丽, 刘芳, 刘雄军. Cu60Zr30Ti10非晶合金弛豫和晶化过程的小角X射线散射研究. , 2006, 55(12): 6673-6676. doi: 10.7498/aps.55.6673
[20]	周效锋, 陶淑芬, 刘佐权, 阚家德, 李德修. Fe73.5Cu1Nb3Si13.5B9非晶合金的激波纳米晶化速率和晶化度的对比研究. , 2002, 51(2): 322-325. doi: 10.7498/aps.51.322

计量

文章访问数: 15048
PDF下载量: 675
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

非晶态物质原子局域连接度与弛豫动力学