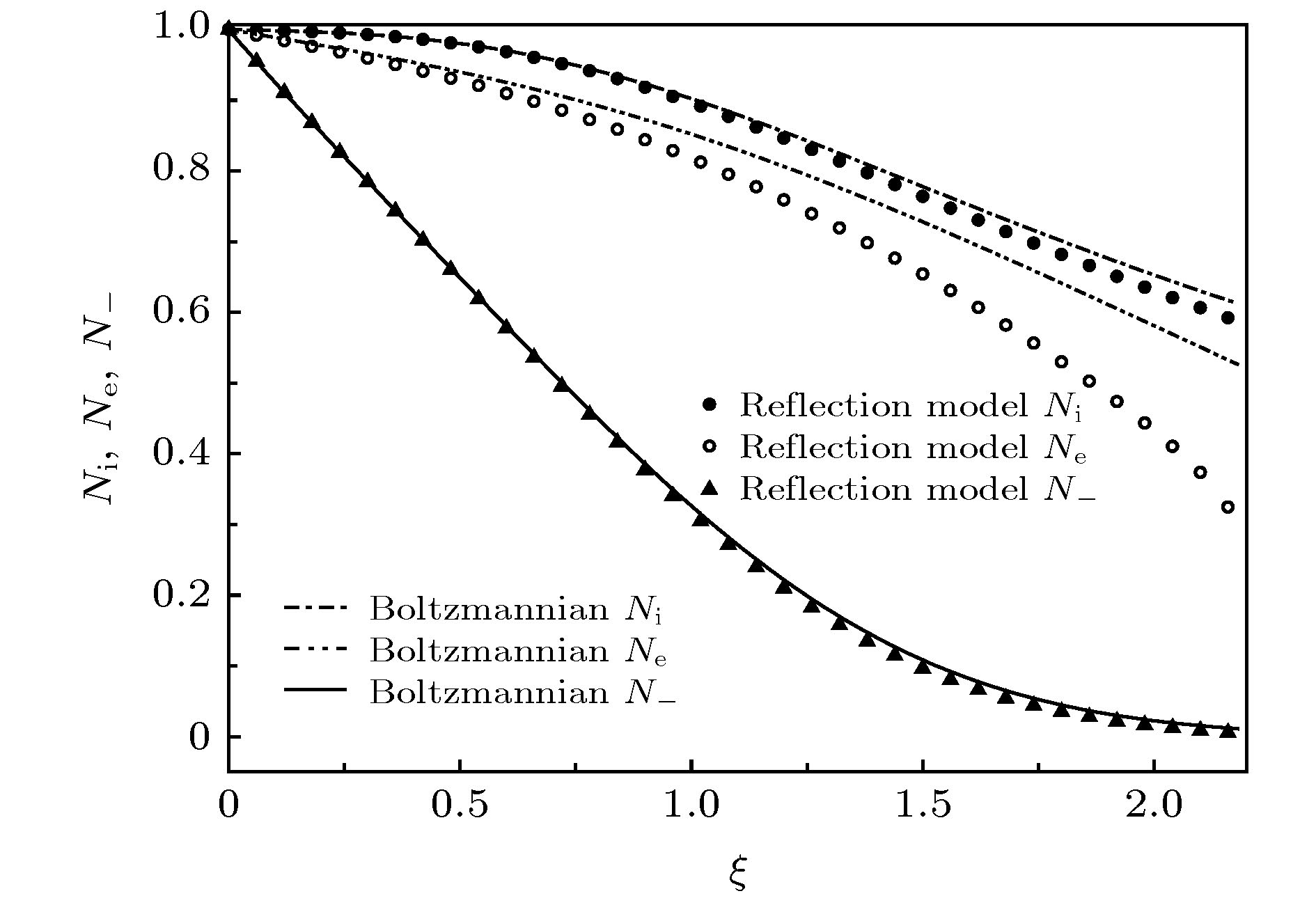
-
研究了鞘层中电子和负离子的反射运动对碰撞电负性磁鞘玻姆判据和鞘层结构的影响. 通过理论推导得到了考虑鞘层中电子和负离子的反射运动时鞘层玻姆判据表达式, 并通过数值模拟得到了电子和负离子采用玻尔兹曼模型和反射运动模型时离子马赫数的下限随参数的变化曲线以及鞘层中带电粒子密度的分布曲线. 结果表明, 电子和负离子的反射运动模型和玻尔兹曼模型离子马赫数的上限完全相同, 下限表达式不同, 反射运动模型中下限还与基板电势有关, 且随着基板电势值的增加而增大, 达到与玻尔兹曼分布中相同值后保持不变, 随着鞘边负离子浓度和温度的不同达到最大值的速度不同; 离子马赫数的下限在玻尔兹曼和反射运动模型中都随鞘边负离子浓度的增加和温度的降低而减小, 只是在反射运动模型中的最大值要小; 两种模型中离子马赫数的下限都随鞘边电场的增加而增加, 但在玻尔兹曼模型中增加得更快最终值更大; 两种模型离子马赫数的下限都随碰撞参数或磁场角度的增加而降低, 但在玻尔兹曼模型中降低更快, 随着碰撞参数或者磁场角度的增加两种模型中离子马赫数的下限趋于一致; 当基板电势值较小时, 电子和负离子的反射运动对鞘层结构影响较大, 当基板电势值较大时电子和负离子反射运动对鞘层中带电粒子密度分布的影响很小.The effects of the reflection of electrons and negative ions in magnetized electronegative and collisional plasma sheath on the Bohm criterion and the sheath structure are numerically investigated. The Bohm criterion expression of the sheath with considering the reflection of electrons and negative ions is derived theoretically. The lower limit of ion Mach number versus parameters and the distribution curve of charged particle density in sheath are obtained by numerical simulation when Boltzmannian model and reflection model are applied to electrons and negative ions. The results show that the upper limit of ion Mach number is identical to that of Boltzmannian model, but their lower limit expressions are different. The lower limit of ion Mach number in the reflection model is also related to the wall potential, and with the increase of the wall potential, ion Mach number first increases and then remains unchanged after reaching the same value as that from Boltzmannian model, and the speeds of their reaching the maximum values are different due to the difference in sheath edge negative ion concentration and temperature. In both Boltzmannian and the reflection model, the lower limit of the ion Mach number decreases with the concentration of the negative ion at the sheath edge increasing and the negative ion temperature decreasing, but the maximum value is smaller in the reflection model. The lower limit of ion Mach number for each of the two models increases with sheath edge electric field increasing, but increases faster and the final value is larger in Boltzmannian model. The lower limit of ion Mach number for each of the two models decreases with the increase of collision parameter or magnetic field angle, but decreases faster in Boltzmannian model with the increase of collision parameter or magnetic field angle. The lower limits of ion Mach number in the two models tend to be the same with the increase of magnetic field angle. When the wall potential is small, the reflection of electrons and negative ions has a great influence on the sheath structure. When the wall potential is large, the reflection of electrons and negative ions have little effect on the density distribution of charged particles in the sheath.
-
Keywords:
- reflection of electrons and negative ions /
- magnetized electronegative sheath /
- Bohm criterion /
- sheath structure
[1] Yamada H, Yoshida Z 1992 J. Plasma Phys. 48 229
Google Scholar
[2] Femandez Palop J I, Ballesteros J, Colomer V, Hemandez M A, Dengra A 1995 J. Appl. Phys. 77 2937
Google Scholar
[3] Femandez Palop J I, Colomer V, Ballesteros J, Hemandez M A, Dengra A 1996 Surf. Coat. Technol. 84 341
Google Scholar
[4] Amemiya H, Annaratone B M, Allen J E 1998 J. Plasma. Phys. 60 81
Google Scholar
[5] Ming L, Michael A V, Steven K D, Brett M J 2000 IEEE Trans. Plasma Sci. 28 248
Google Scholar
[6] WANG Z X, Liu J Y, Zou X, Liu Y, Wang X G 2003 Chin. Phys. Lett. 20 1537
Google Scholar
[7] Yasserian K, Aslaninejad M, Ghoranneviss M 2009 Phys. Plasmas 16 023504
Google Scholar
[8] Hatami M M, Shokri B, Niknam A R 2008 Phys. Plasmas 15 123501
Google Scholar
[9] Gong Y, Duan P, Zhang J H, Zou X, Liu J Y, Liu Y 2010 Chin. J. Comput. Phys. 27 883
[10] Liu J Y, Wang Z X, Wang X G 2003 Phys. Plasmas 10 3032
Google Scholar
[11] Ghomi H, Khoramabadi M, Shukla P K, Ghorannevis M 2010 J. Appl. Phys. 108 063302
Google Scholar
[12] Ghomi H, Khoramabadi M 2010 J. Plasma. Phys. 76 247
Google Scholar
[13] Zou X, Liu H P, Qiu M H, Sun X H 2011 Chin. Phys. Lett. 28 125201
Google Scholar
[14] Ghomi H Khoramabadi M 2011 J Fusion Energ 30 481
Google Scholar
[15] 刘惠平, 邹秀, 邹滨雁, 邱明辉 2012 61 035201
Google Scholar
Liu H P, Zou X, Zou B Y, Qiu M H 2012 Acta Phys. Sin. 61 035201
Google Scholar
[16] 邱明辉, 刘惠平, 邹秀 2012 61 155204
Google Scholar
Qiu M H, Liu H P, Zou X 2012 Acta Phys. Sin. 61 155204
Google Scholar
[17] Hatami M M, Shokri B 2013 Phys. Plasmas 20 033506
Google Scholar
[18] Li J J, Ma J X, Wei Z A 2013 Phys. Plasmas 20 063503
Google Scholar
[19] Yasserian K, Aslaninejad M, Borghei M, Eshghabadi M 2010 J. Theor. Appl. Phys. 4 26
[20] Yasserian K, Aslaninejad M 2012 Phys. Plasmas 19 073507
Google Scholar
[21] Shaw A K, Kar S, Goswami K S 2012 Phys. Plasmas 19 102108
Google Scholar
[22] Moulick R, Mahanta M K, Goswami K S 2013 Phys. Plasmas 20 094501
Google Scholar
[23] 刘惠平, 邹秀, 邹滨雁, 邱明辉 2016 65 245201
Google Scholar
Liu H P, Zou X, Zou B Y, Qiu M H 2016 Acta Phys. Sin. 65 245201
Google Scholar
[24] Sobolewski M A, Wang Y C, Goyette A 2017 J. Appl. Phys. 122 053302
Google Scholar
[25] Regodon G F, Femandez-Palop J I, Tejero-del-Caz A, Diaz-Cabrera J M, Carmona-Cabezas R, Ballesteros J 2018 Plasma Sources Sci. Technol. 2018 27
[26] Oudini N, Sirse N, Taccogna F, Ellingboe A R, Bendib A 2018 Phys. Plasmas 25 053510
Google Scholar
[27] Sternberg N, Poggie J 2004 IEEE Trans. Plasma Sci. 32 2217
Google Scholar
[28] Tskhakaya D D, Shukla P K, Eliasson B, Kuhn S 2005 Phys. Plasmas 12 103503
Google Scholar
[29] Pandey B P, Samarian A, Vladimirov S V 2007 Phys. Plasmas 14 093703
Google Scholar
[30] Zimmermann T M G, Coppins M, Allen J E 2009 Phys. Plasmas 16 043501
Google Scholar
[31] Zimmermann T M G, Coppins M, Allen J E 2010 Phys. Plasmas 17 022301
Google Scholar
[32] Krasheninnikova N S, Tang X, Roytershteyn V S 2010 Phys. Plasmas 17 057103
Google Scholar
[33] Sheehan J P, Hershkowitz N, Kaganovich I D, Wang H, Raitses Y, Barnat E V, Weatherford B R, Sydorenko D 2013 Phys. Rev. Lett. 111 075002
Google Scholar
[34] Sheehan J P, Kaganovich I D, Wang H, Sydorenko D, Raitses Y, Hershkowitz N 2014 Phys. Plasmas 21 063502
Google Scholar
[35] Wang T T, Ma J X, Wei Z A 2015 Phys. Plasmas 22 093505
Google Scholar
[36] Liu J Y, Wang F, Sun J Z 2011 Phys. Plasmas 18 013506
Google Scholar
[37] 邹秀, 邹滨雁, 籍延坤 2010 59 1902
Google Scholar
Zou X, Zou B Y, Ji Y K 2010 Acta Phys. Sin. 59 1902
Google Scholar
-
图 1 电负性等离子体磁鞘模型示意图
Fig. 1. Geometry of the electronegative magnetized plasma sheath model.
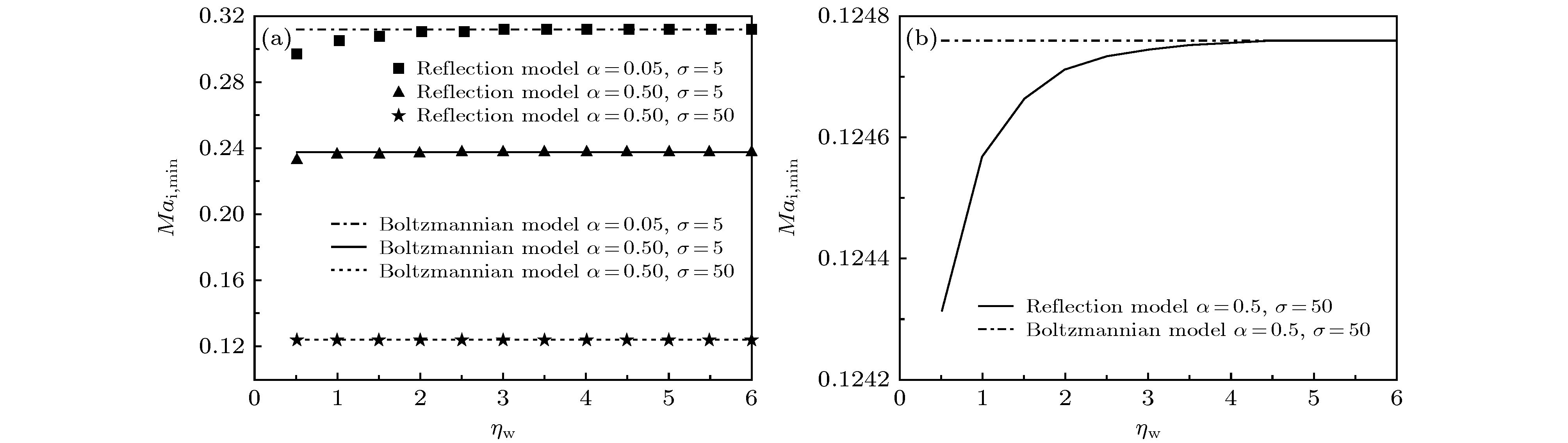
图 2 负离子浓度和温度对离子马赫数下限的影响(
$\nu = 0.1$ ,$B = 0.1 \;{\rm T}$ ,$\theta = {30^ \circ }$ ,${E_0} = 0.05$ ,${\eta _{\rm{w}}} = 0.3$ ) (a)玻尔兹曼模型; (b)反射模型Fig. 2. The effects of negative ions concentration and temperature on the lower limit of ion Mach number (
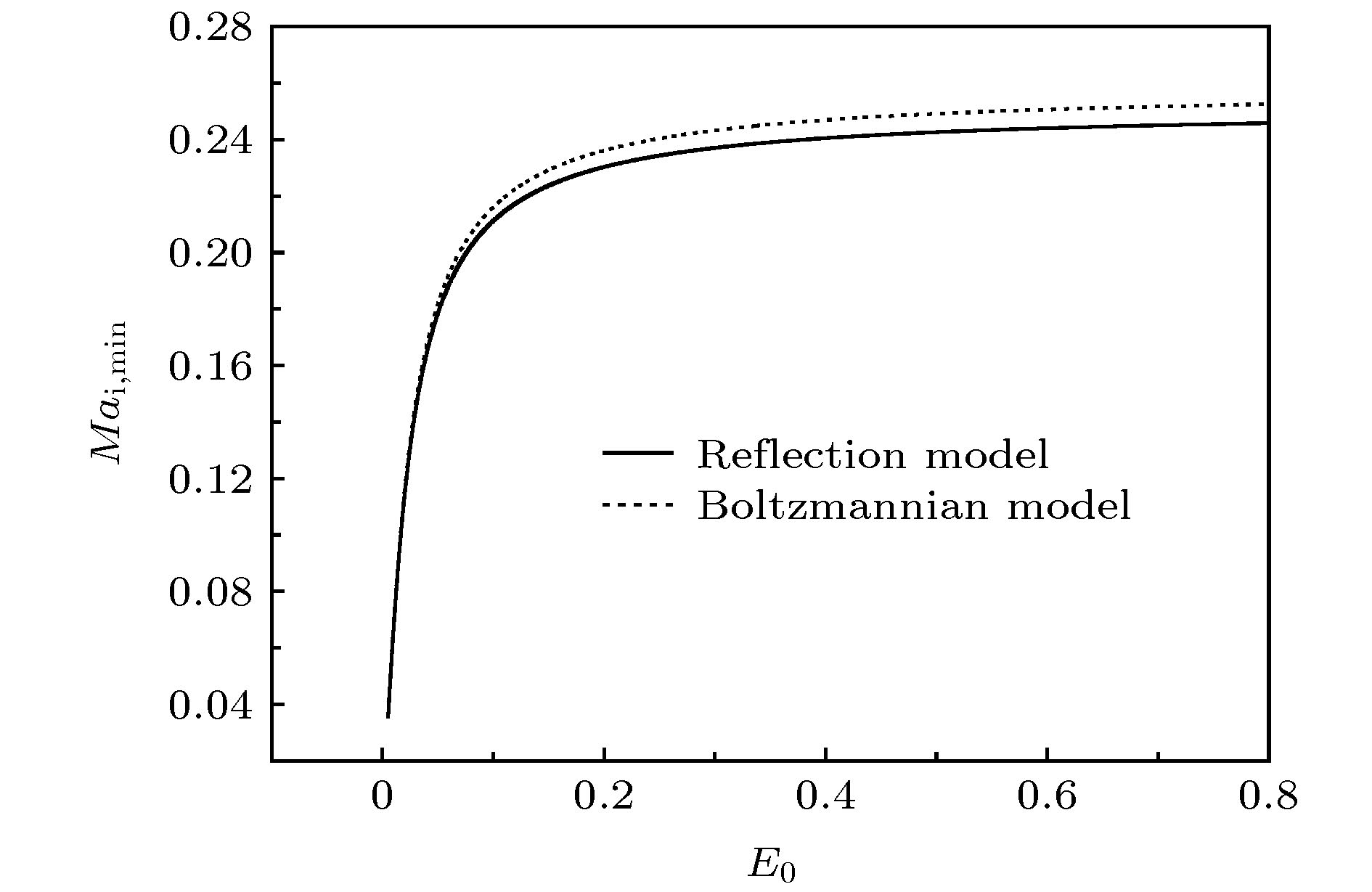
$\nu = 0.1$ ,$B = 0.1 \;{\rm T}$ ,$\theta = {30^ \circ }$ ,${E_0} = 0.05$ ,${\eta _{\rm{w}}} = 0.3$ ): (a) Boltzmannian model; (b) reflection model.
图 3 基板电势对离子马赫数下限的影响 (a)整体; (b)局部 (
$\nu = 0.1$ ,$ B = 0.1 \;{\rm T}$ ,$\theta = {30^ \circ }$ ,${E_0} = 0.05$ )Fig. 3. The effect of wall potential on the lower limit of ion Mach number: (a) Whole; (b) part (
$\nu = 0.1$ ,$B = 0.1 \;{\rm T}$ ,$\theta = {30^ \circ }$ ,${E_0} = 0.05$ ).
图 4 鞘边电场对离子马赫数下限的影响(
$\nu = 0.1$ ,$B = 0.1 \;{\rm T}$ ,$\theta = {30^ \circ }$ ,$\alpha = 0.2$ ,$\sigma = 50$ ,${\eta _{\rm{w}}} = 0.3$ )Fig. 4. The effect of the sheath edge electric field on the lower limit of ion Mach number (
$\nu = 0.1$ ,$B = 0.1 \;{\rm T}$ ,$\theta = {30^ \circ }$ ,$\alpha = 0.2$ ,$\sigma = 50$ ,${\eta _{\rm{w}}} = 0.3$ ).
图 5 碰撞参数对离子马赫数下限的影响(
${E_0} = 0.05$ ,$B = 0.1 \;{\rm T}$ ,$\theta = {30^ \circ }$ ,$\alpha = 0.2$ ,$\sigma = 50$ ,${\eta _{\rm{w}}} = 0.3$ )Fig. 5. The effect of collision parameter on the lower limit of ion Mach number (
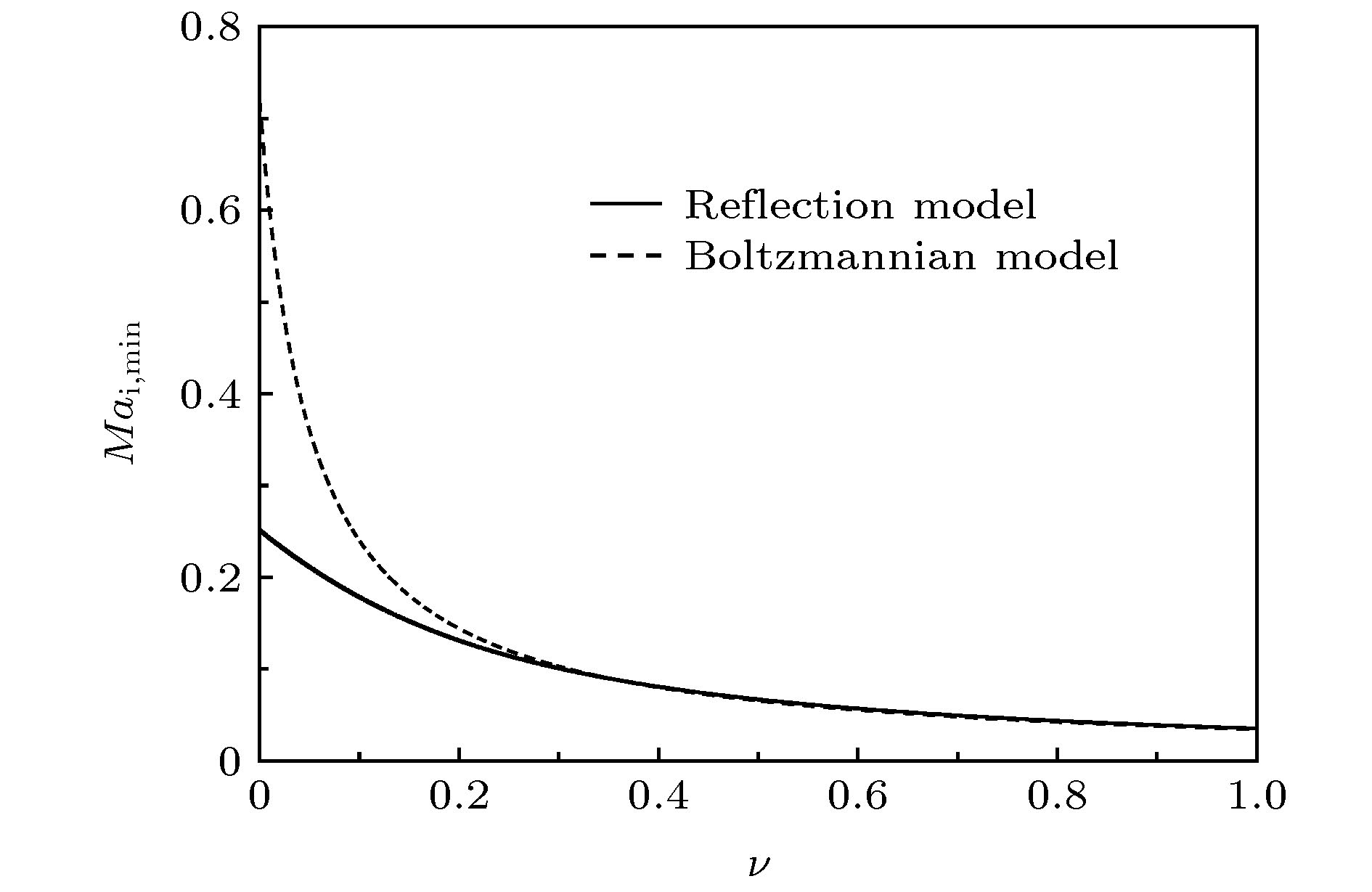
${E_0} = 0.05$ ,$B = 0.1 \;{\rm T}$ ,$\theta = {30^ \circ }$ ,$\alpha = 0.2$ ,$\sigma = 50$ ,${\eta _{\rm{w}}} = 0.3$ ).
图 6 磁场角度对离子马赫数下限的影响(
${E_0} = 0.05$ ,$B = 0.1\;{\rm{ T}}$ ,$\nu = 0.1$ ,$\alpha = 0.2$ ,$\sigma = 50$ ,${\eta _{\rm{w}}} = 0.3$ )Fig. 6. The effect of magnetic field angle on the lower limit of ion Mach number (
${E_0} = 0.05$ ,$B = 0.1\;{\rm{ T}}$ ,$\nu = 0.1$ ,$\alpha = 0.2$ ,$\sigma = 50$ ,${\eta _{\rm{w}}} = 0.3$ ).
图 7 鞘层中带电粒子密度分布(
${\eta _{\rm{w}}} = 0.7$ )Fig. 7. The normalized charged particle density (
${\eta _{\rm{w}}} = 0.7$ ).
图 8 鞘层中带电粒子密度分布(
${\eta _{\rm{w}}} = 10$ )Fig. 8. The normalized charged particle density (
${\eta _{\rm{w}}} = 10$ ). -
[1] Yamada H, Yoshida Z 1992 J. Plasma Phys. 48 229
Google Scholar
[2] Femandez Palop J I, Ballesteros J, Colomer V, Hemandez M A, Dengra A 1995 J. Appl. Phys. 77 2937
Google Scholar
[3] Femandez Palop J I, Colomer V, Ballesteros J, Hemandez M A, Dengra A 1996 Surf. Coat. Technol. 84 341
Google Scholar
[4] Amemiya H, Annaratone B M, Allen J E 1998 J. Plasma. Phys. 60 81
Google Scholar
[5] Ming L, Michael A V, Steven K D, Brett M J 2000 IEEE Trans. Plasma Sci. 28 248
Google Scholar
[6] WANG Z X, Liu J Y, Zou X, Liu Y, Wang X G 2003 Chin. Phys. Lett. 20 1537
Google Scholar
[7] Yasserian K, Aslaninejad M, Ghoranneviss M 2009 Phys. Plasmas 16 023504
Google Scholar
[8] Hatami M M, Shokri B, Niknam A R 2008 Phys. Plasmas 15 123501
Google Scholar
[9] Gong Y, Duan P, Zhang J H, Zou X, Liu J Y, Liu Y 2010 Chin. J. Comput. Phys. 27 883
[10] Liu J Y, Wang Z X, Wang X G 2003 Phys. Plasmas 10 3032
Google Scholar
[11] Ghomi H, Khoramabadi M, Shukla P K, Ghorannevis M 2010 J. Appl. Phys. 108 063302
Google Scholar
[12] Ghomi H, Khoramabadi M 2010 J. Plasma. Phys. 76 247
Google Scholar
[13] Zou X, Liu H P, Qiu M H, Sun X H 2011 Chin. Phys. Lett. 28 125201
Google Scholar
[14] Ghomi H Khoramabadi M 2011 J Fusion Energ 30 481
Google Scholar
[15] 刘惠平, 邹秀, 邹滨雁, 邱明辉 2012 61 035201
Google Scholar
Liu H P, Zou X, Zou B Y, Qiu M H 2012 Acta Phys. Sin. 61 035201
Google Scholar
[16] 邱明辉, 刘惠平, 邹秀 2012 61 155204
Google Scholar
Qiu M H, Liu H P, Zou X 2012 Acta Phys. Sin. 61 155204
Google Scholar
[17] Hatami M M, Shokri B 2013 Phys. Plasmas 20 033506
Google Scholar
[18] Li J J, Ma J X, Wei Z A 2013 Phys. Plasmas 20 063503
Google Scholar
[19] Yasserian K, Aslaninejad M, Borghei M, Eshghabadi M 2010 J. Theor. Appl. Phys. 4 26
[20] Yasserian K, Aslaninejad M 2012 Phys. Plasmas 19 073507
Google Scholar
[21] Shaw A K, Kar S, Goswami K S 2012 Phys. Plasmas 19 102108
Google Scholar
[22] Moulick R, Mahanta M K, Goswami K S 2013 Phys. Plasmas 20 094501
Google Scholar
[23] 刘惠平, 邹秀, 邹滨雁, 邱明辉 2016 65 245201
Google Scholar
Liu H P, Zou X, Zou B Y, Qiu M H 2016 Acta Phys. Sin. 65 245201
Google Scholar
[24] Sobolewski M A, Wang Y C, Goyette A 2017 J. Appl. Phys. 122 053302
Google Scholar
[25] Regodon G F, Femandez-Palop J I, Tejero-del-Caz A, Diaz-Cabrera J M, Carmona-Cabezas R, Ballesteros J 2018 Plasma Sources Sci. Technol. 2018 27
[26] Oudini N, Sirse N, Taccogna F, Ellingboe A R, Bendib A 2018 Phys. Plasmas 25 053510
Google Scholar
[27] Sternberg N, Poggie J 2004 IEEE Trans. Plasma Sci. 32 2217
Google Scholar
[28] Tskhakaya D D, Shukla P K, Eliasson B, Kuhn S 2005 Phys. Plasmas 12 103503
Google Scholar
[29] Pandey B P, Samarian A, Vladimirov S V 2007 Phys. Plasmas 14 093703
Google Scholar
[30] Zimmermann T M G, Coppins M, Allen J E 2009 Phys. Plasmas 16 043501
Google Scholar
[31] Zimmermann T M G, Coppins M, Allen J E 2010 Phys. Plasmas 17 022301
Google Scholar
[32] Krasheninnikova N S, Tang X, Roytershteyn V S 2010 Phys. Plasmas 17 057103
Google Scholar
[33] Sheehan J P, Hershkowitz N, Kaganovich I D, Wang H, Raitses Y, Barnat E V, Weatherford B R, Sydorenko D 2013 Phys. Rev. Lett. 111 075002
Google Scholar
[34] Sheehan J P, Kaganovich I D, Wang H, Sydorenko D, Raitses Y, Hershkowitz N 2014 Phys. Plasmas 21 063502
Google Scholar
[35] Wang T T, Ma J X, Wei Z A 2015 Phys. Plasmas 22 093505
Google Scholar
[36] Liu J Y, Wang F, Sun J Z 2011 Phys. Plasmas 18 013506
Google Scholar
[37] 邹秀, 邹滨雁, 籍延坤 2010 59 1902
Google Scholar
Zou X, Zou B Y, Ji Y K 2010 Acta Phys. Sin. 59 1902
Google Scholar
下载:
计量
- 文章访问数: 6069
- PDF下载量: 124
- 被引次数: 0
