15 MA Z箍缩装置真空磁绝缘传输线鞘层电子流分析

龚振洲; 魏浩; 范思源; 洪亚平; 吴撼宇; 邱爱慈

doi:10.7498/aps.72.20221901

摘要

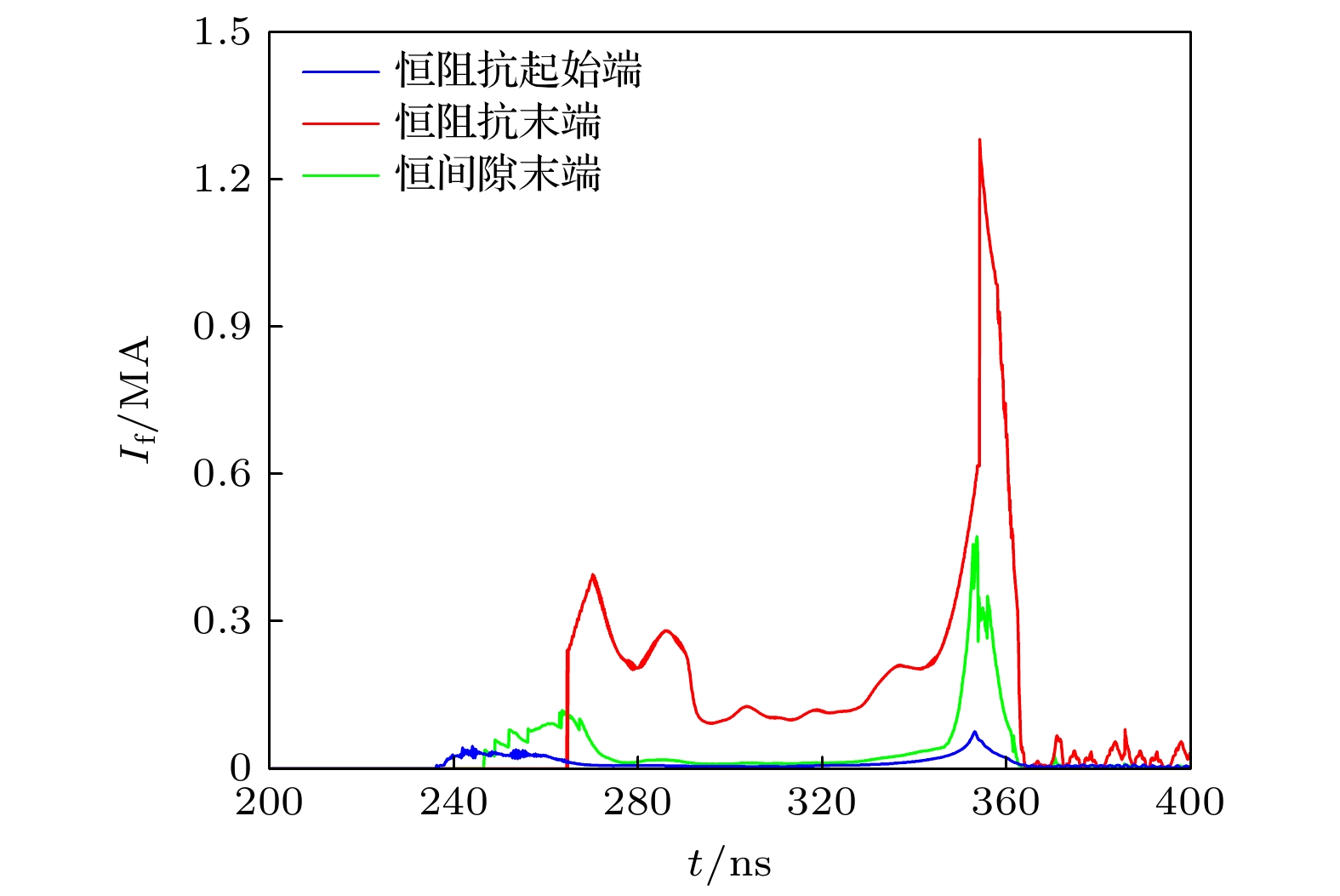
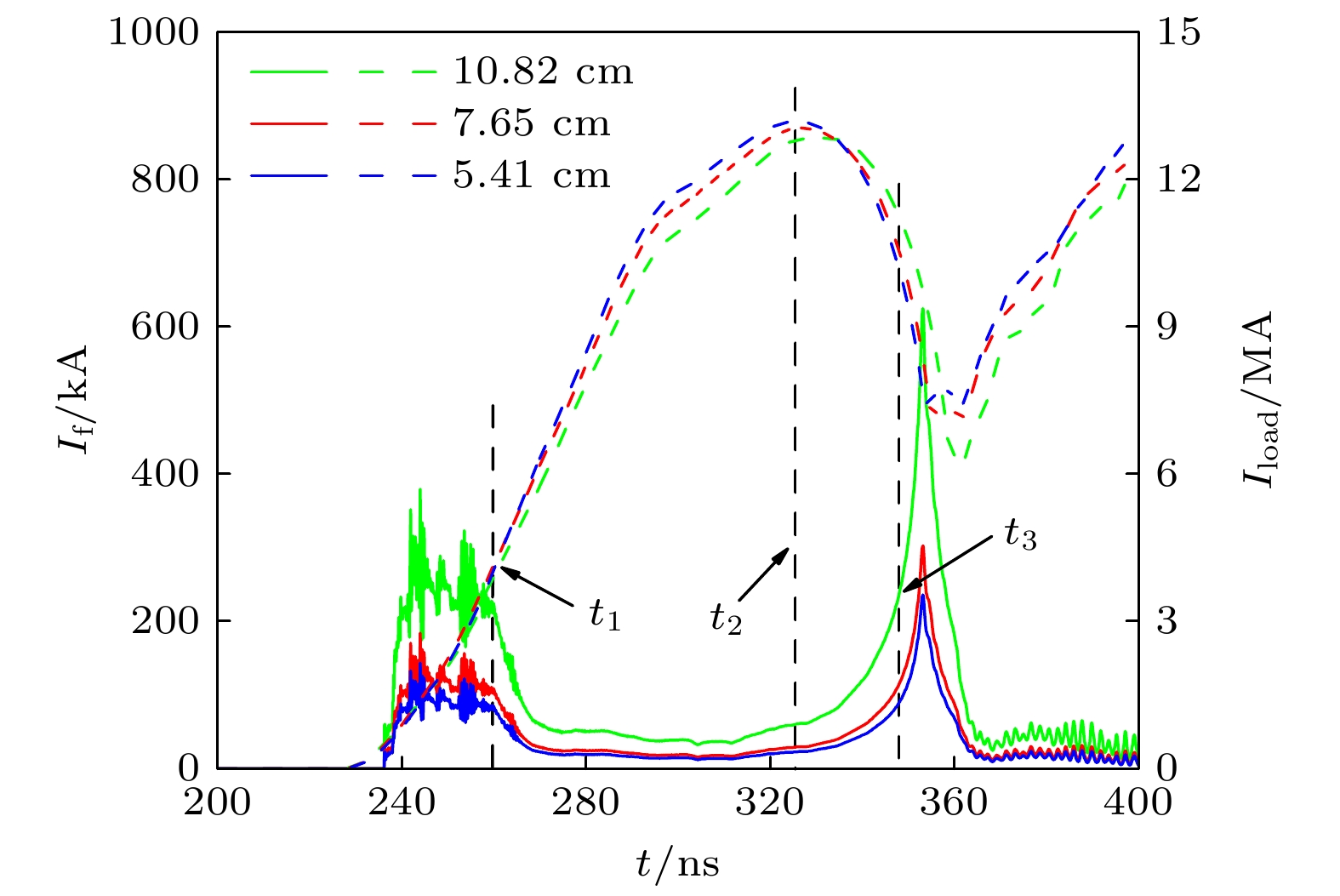
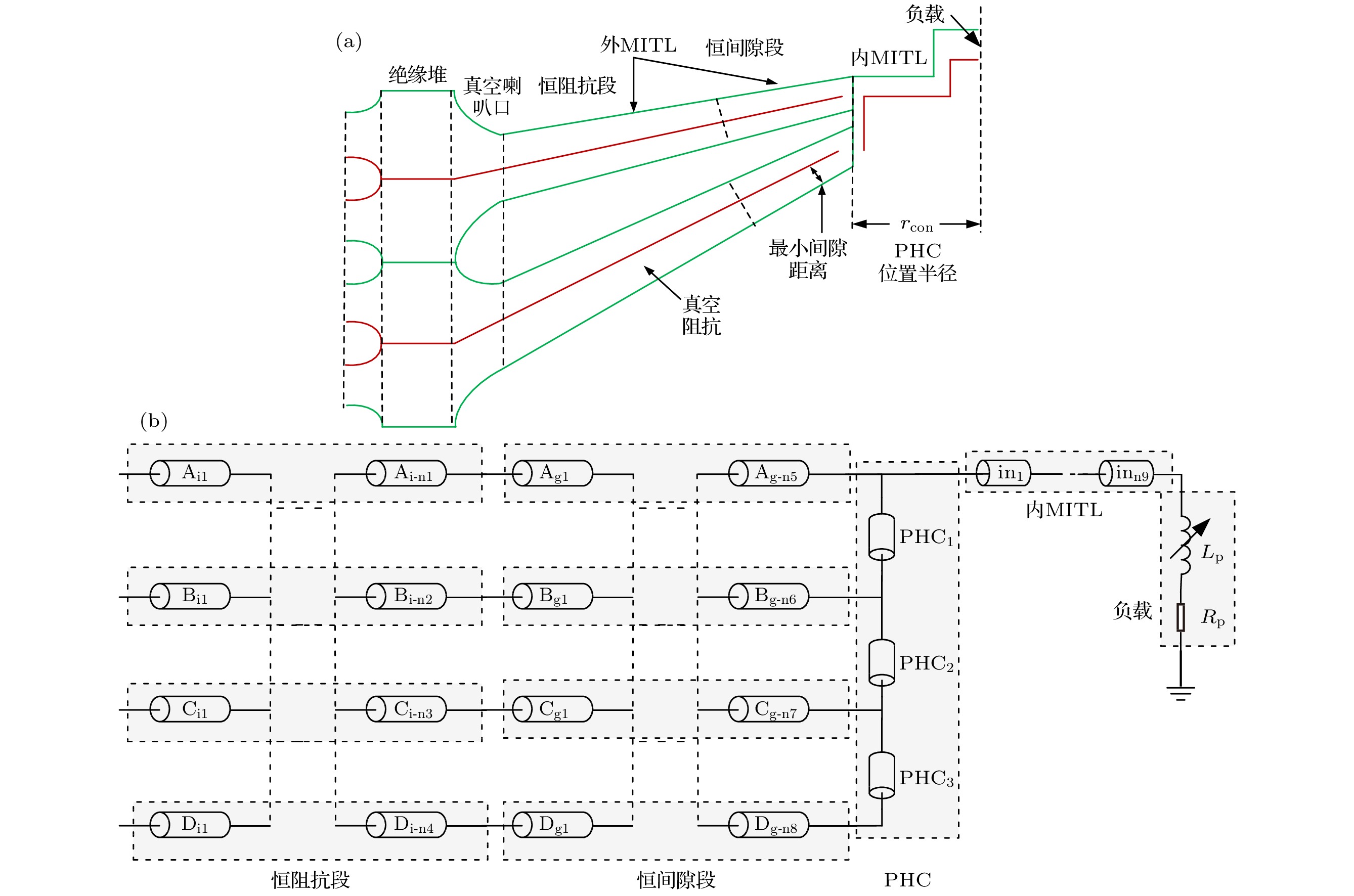
基于建立的15 MA Z箍缩装置等效电路模型, 获得了外层磁绝缘传输线(magnetically-insulated transmission line, MITL)鞘层电子流分布规律: 从时间上看, 鞘层电子流幅值先减小、后增大, 波形呈“马鞍”型; 从空间上看, 鞘层电子流沿着功率流方向逐渐减小. 分析了MITL参数, 包括恒阻抗段真空阻抗、恒间隙段间距, 以及柱孔盘旋面位置半径对MITL末端鞘层电子流的影响. 计算结果显示: MITL末端鞘层电子流受MITL末端阻抗和柱孔盘旋面位置半径的影响较大. 当15 MA装置四层MITL并联真空阻抗从0.42 Ω增大到0.84 Ω时, 在负载聚爆前5 ns时刻, MITL末端鞘层电子流从184.7 kA降低至106.9 kA, 负载峰值电流减小约0.5 MA.

关键词:

Abstract

The 15-MA driver is powered by 24 linear-transformer-driver (LTD) modules connected electrically in parallel. The magnetically-insulated-transmission-line (MITL) system of the 15-MA driver adopts a four-level design. It is expected that the primary source delivers a more than 15 MA current to a physics load. The typical one-dimensional steady-state pressure-balance model is adopted to calculate the electron flow current of the outer MITLs of the 15-MA driver after the magnetic insulation has been established. The cathode plasma expansion and the collisional flow electrons are considered on the basis of that model. Multiple designs with different characteristic parameters of the MITL system include the vacuum impedance of the constant-impedance segment of the outer-MITL, the minimum gap of the outer-MITL, and the location of the post-hole convolute (PHC). The flow currents of these designs are calculated in three typical times (1/3 peak load current time, peak load current time, and 5 ns before the Z-pinch stagnation) by establishing the equivalent circuit model of the 15-MA driver. The influences of these characteristic parameters on the electrical pulse transmission and convergence of the 15 MA driver are obtained. The calculation results show that the electron flow current at the end of MITL is greatly affected by the impedance of the end of MITL after the electron flow current has entered into the steady state magnetic insulation. The flow current decreases from 184.7 kA to 106.9 kA, while the load current is reduced by 0.5 MA, as the vacuum impedance increases from 0.42 Ω to 0.84 Ω. This is mainly because the central inductance increases by about 1.43 nH (from 9.94 nH to 11.37 nH). In the time of 5 ns before load stagnation, the flow current decreases from 181.9 kA to 85.1 kA as the minimum gap of the outer-MITL increases from 7.10 mm to 14.00 mm, and the peak load current drops only by about 0.1 MA. The flow current and load current decrease slowly as the location radius of the PHC decreases until the radius decreases to 7.65 mm. The research in this paper is helpful in guiding the structure optimization for the central converging region of future Z-pinch driver.

Keywords:

Z-pinch /
magnetically insulated transmission line /
electron flow current /
vacuum impedance

作者及机构信息

1.
西安交通大学, 电力设备与电气绝缘国家重点实验室, 西安　710049

2.
西北核技术研究所, 强脉冲辐射环境模拟与效应国家重点实验室, 西安　710024

通信作者: 魏浩, weihaoyy@sina.com

基金项目: 国家自然科学基金(批准号: 51790524, 11975186)资助的课题.

Authors and contacts

1.
State Key Laboratory of Electrical Insulation and Power Equipment, Xi’an Jiaotong University, Xi’an 710049, China

2.
State Key Laboratory of Intense Pulsed Radiation Simulation and Effect, Northwest Institute of Nuclear Technology, Xi’an 710024, China

Corresponding author: Wei Hao, weihaoyy@sina.com

Funds: Project supported by the National Natural Science Foundation of China (Grant Nos. 51790524, 11975186).

文章全文 : translate this paragraph

参考文献

[1]	Hutsel B T, Corcoran P A, Cuneo M E, et al. 2018 Phys. Rev. ST Accel. Beams 21 030401 Google Scholar
[2]	邹文康, 郭帆, 王贵林, 陈林, 卫兵, 宋盛义 2015 高电压技术 41 1844 Google Scholar Zou W K, Guo F, Wang G L, Chen L, Wei B, Song S Y 2015 High Volt. Eng. 41 1844 Google Scholar
[3]	Deng J J, Xie W P, Feng S P, et al. 2016 Matter Radiat. Extremes 1 48 Google Scholar
[4]	Stygar W A, Awe T J, Bailey J E, et al. 2015 Phys. Rev. ST Accel. Beams 18 110401 Google Scholar
[5]	Spielman R B, Froula D H, Brent G, et al. 2017 Matter Radiat. Extremes 5 204 Google Scholar
[6]	Spielman R B, Reisman D B 2019 Matter Radiat. Extremes 4 027402 Google Scholar
[7]	Chen L, Zou W K, Zhou L J, et al. 2019 Phys. Rev. Accel. Beams 22 030401 Google Scholar
[8]	Madrid E A, Rose D V, Welch D R, et al. 2013 Phys. Rev. ST Accel. Beams 16 120401 Google Scholar
[9]	Rose D V, Madrid E A, Welch D R, Clark R E, Mostrom C B, Stygar W A, Cuneo M E 2015 Phys. Rev. ST Accel. Beams 18 030402 Google Scholar
[10]	Gomez M R, Gilgenbach R M, Cuneo M E, et al. 2017 Phys. Rev. ST Accel. Beams 20 010401 Google Scholar
[11]	Waisman E M, Desjarlais M P, Cuneo M E 2019 Phys. Rev. Accel. Beams 22 030402 Google Scholar
[12]	Rose D V, Waisman E M, Desjarlais M P, Hutsel B T, Cuneo M E, Welch D, Bennett N, Laity G R 2020 Phys. Rev. Accel. Beams 23 080401 Google Scholar
[13]	Mazarakis M G, Cuneo M E, Fowler W E, et al. 2013 The 19 th IEEE Pulsed Power Conference San Francisco, CA, USA, June 16−21 2013 p1
[14]	Bennett N, Welch D R, Jennings C A, et al. 2019 Phys. Rev. Accel. Beams 22 120401 Google Scholar
[15]	Bennett N, Welch D R, Laity G, Rose D V, Cuneo M E 2021 Phys. Rev. Accel. Beams 24 060401 Google Scholar
[16]	Welch D R, Bennett N, Genoni T C, Thoma C, Rose. D V 2020 Phys. Rev. Accel. Beams 23 110401 Google Scholar
[17]	龚振洲, 魏浩, 范思源, 孙凤举, 吴撼宇, 邱爱慈 2022 71 105202 Google Scholar Gong Z Z, Wei H, Fan S Y, Sun F J, Wu H Y, Qiu A C 2022 Acta Phys. Sin. 71 105202 Google Scholar
[18]	Stygar W A, Wagoner T C, Ives H C, et al. 2006 Phys. Rev. ST Accel. Beams 9 090401 Google Scholar
[19]	Stygar W A, Corcoran P A, Ives H C, et al. 2009 Phys. Rev. ST Accel. Beams 12 120401 Google Scholar
[20]	Jennings C A, Chittenden J P, Cuneo M E, et al. 2010 IEEE Trans. Plasma Sci. 38 529 Google Scholar

施引文献

图 1 15 MA装置中心汇流区示意图　(a) MITL结构示意图; (b)电路编码示意图

Fig. 1. Cross-sectional view of the central converging region of the 15 MA driver: (a) Schematic drawing of MITL; (b) coding diagram.

下载: 全尺寸图片幻灯片

图 2 三种模型计算15 MA装置MITL末端鞘层电子流对比

Fig. 2. Comparison of the electron flow currents of the 15 MA driver of the three models.

下载: 全尺寸图片幻灯片

图 3 15 MA装置D层MITL三个典型位置鞘层电子流对比

Fig. 3. Comparison of the electron flow currents in three typical locations of D-level MITL of the 15 MA driver.

下载: 全尺寸图片幻灯片

图 4 外层MITL恒阻抗段真空阻抗对鞘层电子流和负载电流的影响, 图中虚线表示负载电流, 实线表示鞘层电子流

Fig. 4. Influence of the vacuum impedance of constant-impedance MITL on the electron flow current and load current. The dotted lines in the figure represent the load currents, and the solid lines represent the electron flow currents.

下载: 全尺寸图片幻灯片

图 5 外层MITL最小间隙距离对鞘层电子流和负载电流的影响, 图中虚线表示负载电流, 实线表示鞘层电子流

Fig. 5. Influence of the minimum gap of outer MITL on the electron flow current and load current. The dotted lines in the figure represent the load currents, and the solid lines represent the electron flow currents.

下载: 全尺寸图片幻灯片

图 6 PHC位置半径对鞘层电子流和负载电流的影响, 图中虚线表示负载电流, 实线表示鞘层电子流

Fig. 6. Influence of the location of PHC on the electron flow current and load current. The dotted lines in the figure represent the load currents, and the solid lines represent the electron flow currents.

下载: 全尺寸图片幻灯片

表 1 几种MITL典型参数对比

Table 1. Comparison of the structural parameters of the MITL of the different designs.

组	A层阻抗Z_A/Ω	B层阻抗Z_B/Ω	C层阻抗Z_C/Ω	D层阻抗Z_D/Ω	四层并联阻抗Z_MITL/Ω	最小间隙距离h/mm	PHC位置半径r_con/cm	中心区初始电感/nH
Ⅰ	2.83	2.83	4.24	4.24	0.84	10.00	7.65	11.37
Ⅱ	2.00	2.00	3.00	3.00	0.60	10.00	7.65	10.50
Ⅲ	1.41	1.41	2.12	2.12	0.42	10.00	7.65	9.94
Ⅳ	2.00	2.00	3.00	3.00	0.60	14.10	7.65	10.84
Ⅴ	2.00	2.00	3.00	3.00	0.60	7.10	7.65	10.33
Ⅵ	2.00	2.00	3.00	3.00	0.60	10.00	10.82	10.90
Ⅶ	2.00	2.00	3.00	3.00	0.60	10.00	5.41	10.11

下载: 导出CSV

map

[1]	Hutsel B T, Corcoran P A, Cuneo M E, et al. 2018 Phys. Rev. ST Accel. Beams 21 030401 Google Scholar
[2]	邹文康, 郭帆, 王贵林, 陈林, 卫兵, 宋盛义 2015 高电压技术 41 1844 Google Scholar Zou W K, Guo F, Wang G L, Chen L, Wei B, Song S Y 2015 High Volt. Eng. 41 1844 Google Scholar
[3]	Deng J J, Xie W P, Feng S P, et al. 2016 Matter Radiat. Extremes 1 48 Google Scholar
[4]	Stygar W A, Awe T J, Bailey J E, et al. 2015 Phys. Rev. ST Accel. Beams 18 110401 Google Scholar
[5]	Spielman R B, Froula D H, Brent G, et al. 2017 Matter Radiat. Extremes 5 204 Google Scholar
[6]	Spielman R B, Reisman D B 2019 Matter Radiat. Extremes 4 027402 Google Scholar
[7]	Chen L, Zou W K, Zhou L J, et al. 2019 Phys. Rev. Accel. Beams 22 030401 Google Scholar
[8]	Madrid E A, Rose D V, Welch D R, et al. 2013 Phys. Rev. ST Accel. Beams 16 120401 Google Scholar
[9]	Rose D V, Madrid E A, Welch D R, Clark R E, Mostrom C B, Stygar W A, Cuneo M E 2015 Phys. Rev. ST Accel. Beams 18 030402 Google Scholar
[10]	Gomez M R, Gilgenbach R M, Cuneo M E, et al. 2017 Phys. Rev. ST Accel. Beams 20 010401 Google Scholar
[11]	Waisman E M, Desjarlais M P, Cuneo M E 2019 Phys. Rev. Accel. Beams 22 030402 Google Scholar
[12]	Rose D V, Waisman E M, Desjarlais M P, Hutsel B T, Cuneo M E, Welch D, Bennett N, Laity G R 2020 Phys. Rev. Accel. Beams 23 080401 Google Scholar
[13]	Mazarakis M G, Cuneo M E, Fowler W E, et al. 2013 The 19 th IEEE Pulsed Power Conference San Francisco, CA, USA, June 16−21 2013 p1
[14]	Bennett N, Welch D R, Jennings C A, et al. 2019 Phys. Rev. Accel. Beams 22 120401 Google Scholar
[15]	Bennett N, Welch D R, Laity G, Rose D V, Cuneo M E 2021 Phys. Rev. Accel. Beams 24 060401 Google Scholar
[16]	Welch D R, Bennett N, Genoni T C, Thoma C, Rose. D V 2020 Phys. Rev. Accel. Beams 23 110401 Google Scholar
[17]	龚振洲, 魏浩, 范思源, 孙凤举, 吴撼宇, 邱爱慈 2022 71 105202 Google Scholar Gong Z Z, Wei H, Fan S Y, Sun F J, Wu H Y, Qiu A C 2022 Acta Phys. Sin. 71 105202 Google Scholar
[18]	Stygar W A, Wagoner T C, Ives H C, et al. 2006 Phys. Rev. ST Accel. Beams 9 090401 Google Scholar
[19]	Stygar W A, Corcoran P A, Ives H C, et al. 2009 Phys. Rev. ST Accel. Beams 12 120401 Google Scholar
[20]	Jennings C A, Chittenden J P, Cuneo M E, et al. 2010 IEEE Trans. Plasma Sci. 38 529 Google Scholar

[1]	龚振洲, 魏浩, 范思源, 孙凤举, 吴撼宇, 邱爱慈. 15 MA Z箍缩装置真空磁绝缘传输线损失电流的电路模拟. , 2022, 71(10): 105202. doi: 10.7498/aps.71.20212378
[2]	周少彤, 任晓东, 黄显宾, 徐强. 一种用于Z箍缩实验的软X射线成像系统. , 2021, 70(4): 045203. doi: 10.7498/aps.70.20200957
[3]	陈忠旺, 宁成. 基于MULTI2D-Z程序的Z箍缩动态黑腔形成过程模拟. , 2017, 66(12): 125202. doi: 10.7498/aps.66.125202
[4]	高启, 张传飞, 周林, 李正宏, 吴泽清, 雷雨, 章春来, 祖小涛. Z箍缩Al等离子体X特征辐射谱线数值模拟及考虑叠加效应后的修正. , 2014, 63(12): 125202. doi: 10.7498/aps.63.125202
[5]	盛亮, 彭博栋, 袁媛, 张美, 李奎念, 张信军, 赵晨, 赵吉祯, 李沫, 王培伟, 李阳. 表面绝缘混合平面丝阵Z箍缩激光阴影图像诊断. , 2014, 63(23): 235205. doi: 10.7498/aps.63.235205
[6]	盛亮, 李阳, 袁媛, 彭博栋, 李沫, 张美, 赵吉祯, 魏福利, 王亮平, 黑东炜, 邱爱慈. 表面绝缘铝平面丝阵Z箍缩实验研究. , 2014, 63(5): 055201. doi: 10.7498/aps.63.055201
[7]	高启, 张传飞, 周林, 李正宏, 吴泽清, 雷雨, 章春来, 祖小涛. Z箍缩Al等离子体X辐射谱线的分离及电子温度的提取. , 2014, 63(9): 095201. doi: 10.7498/aps.63.095201
[8]	但加坤, 任晓东, 黄显宾, 张思群, 周少彤, 段书超, 欧阳凯, 蔡红春, 卫兵, 计策, 何安, 夏明鹤, 丰树平, 王勐, 谢卫平. Z箍缩内爆产生的电磁脉冲辐射. , 2013, 62(24): 245201. doi: 10.7498/aps.62.245201
[9]	叶繁, 薛飞彪, 褚衍运, 司粉妮, 胡青元, 宁家敏, 周林, 杨建伦, 徐荣昆, 李正宏, 许泽平. 双层丝阵Z箍缩电流分配实验研究. , 2013, 62(17): 175203. doi: 10.7498/aps.62.175203
[10]	刘腊群, 刘大刚, 王学琼, 邹文康, 杨超. 带螺旋支撑杆的同轴磁绝缘传输线三维数值模拟的实现. , 2012, 61(16): 162901. doi: 10.7498/aps.61.162901
[11]	周军, 张鹏飞, 杨海亮, 孙江, 孙剑峰, 苏兆锋, 刘万东. 同轴圆柱形磁绝缘传输线前沿损失与工作电压关系. , 2012, 61(24): 245203. doi: 10.7498/aps.61.245203
[12]	盛亮, 邱孟通, 黑东炜, 邱爱慈, 丛培天, 王亮平, 魏福利. 丝阵负载Z箍缩内爆动力学研究. , 2011, 60(5): 055205. doi: 10.7498/aps.60.055205
[13]	盛亮, 王亮平, 李阳, 彭博栋, 张美, 吴坚, 王培伟, 魏福利, 袁媛. 平面丝阵负载Z箍缩内爆动力学一维图像诊断. , 2011, 60(10): 105205. doi: 10.7498/aps.60.105205
[14]	郭帆, 李永东, 王洪广, 刘纯亮, 呼义翔, 张鹏飞, 马萌. Z箍缩装置外磁绝缘传输线全尺寸粒子模拟研究. , 2011, 60(10): 102901. doi: 10.7498/aps.60.102901
[15]	吴刚, 邱爱慈, 吕敏, 蒯斌, 王亮平, 丛培天, 邱孟通, 雷天时, 孙铁平, 郭宁, 韩娟娟, 张信军, 黄涛, 张国伟, 乔开来. “强光一号”Al丝阵Z箍缩产生K层辐射实验研究. , 2009, 58(7): 4779-4786. doi: 10.7498/aps.58.4779
[16]	宁成, 丁宁, 杨震华. “强光一号”装置上部分Z箍缩实验结果的物理分析. , 2007, 56(1): 338-345. doi: 10.7498/aps.56.338
[17]	宁成, 丁宁, 刘全, 杨震华. 双层钨丝阵的Z箍缩动力学过程研究. , 2006, 55(7): 3488-3493. doi: 10.7498/aps.55.3488
[18]	黄显宾, 杨礼兵, 顾元朝, 邓建军, 周荣国, 邹杰, 周少彤, 张思群, 陈光华, 畅里华, 李丰平, 欧阳凯, 李军, 杨亮, 王雄, 张朝辉. 氩气Z箍缩内爆动力学过程实验研究. , 2006, 55(4): 1900-1906. doi: 10.7498/aps.55.1900
[19]	张扬, 丁宁. 轴向流对Z箍缩等离子体稳定性的影响. , 2006, 55(5): 2333-2339. doi: 10.7498/aps.55.2333
[20]	宁成, 李正宏, 华欣生, 徐荣昆, 彭先觉, 许泽平, 杨建伦, 郭存, 蒋世伦, 丰树平, 杨礼兵, 晏成立, 宋凤军, V. P. Smirnov, Yu. G. Kalinin, A. S. Kingsep, A. S. Chernenko, E. V. Grabovsky. 铝-钨丝混编阵的Z-箍缩实验研究. , 2004, 53(7): 2244-2249. doi: 10.7498/aps.53.2244

计量

文章访问数: 3259
PDF下载量: 58
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板