-
根据自由空间光束传输遵循的(3+1)维薛定谔方程, 得到了两束时空自减速艾里复变量拉盖尔高斯(Airy elegent-Laguerre-Gaussian, AELG)光束共线传输时的解析解, 并分析其共线传输时的传输特性. 分析结果表明, 双光束各自的模式指数、组合光束强度的权重因子、初始相位差对光束的传输都会有影响. 本文发现, 通过选择模式参数或者选择它们的相对振幅, 对于共线传输的两束时空自减速AELG光束, 可以有效控制叠加光束的波形形态以及横向传输截面的光斑分布. 特别是当两束光束的模式参数不等于零时, 波包将沿着传输轴发生螺旋形旋转, 其相位图中心位置都会出现涡旋现象. 若该参数值为正, 则光束沿传输轴逆时针旋转, 否则, 光束将沿传输轴呈螺旋形顺时针方向旋转. 通过调整叠加光束的初始相位差, 波包沿传输轴线也将发生旋转, 但这两种旋转特性的旋转机理完全不同. 如果选取两束时空自减速 AELG 光束的角向模式参数m相同, 则叠加光束在传输过程中呈现空心环形状态, 出现空心环形时空自减速 AELG 波包, 且该波包在传输截面上随着传输距离的增加, 多环结构最终湮灭为单环, 并向远方推移, 使得空心部分越来越大.
-
关键词:
- 复变量艾瑞拉盖尔高斯光束 /
- 时空自减速 /
- 共线传输 /
- 空心光束
Based on the (3+1)-dimensional free-space Schrödinger equation, the analytical solutions to the equation for the propagating properties of two three-dimensional collinear self-decelerating Airy-elegant-Laguerre-Gaussian(AELG) light beams in free space are investigated. The different mode numbers, the mode index for each of the collinear beams, weight factor of combined beam, and initial phase difference will affect the profiles of the wave packets, and thus giving the method to control the spatiotemporal profiles during propagation. The spatiotemporal profiles will rotate if none of the mode parameters are equal to zero, and there are vortices in the center of the phase distribution curve. If the mode parameters are positive numbers, the profiles of the beams will rotate in a helical clockwise direction. Otherwise, if the mode parameters are negative numbers,they will rotate in a helical anticlockwise direction during propagation. The wave packets will also rotate when the relative phase is varied. However, the rotation principles of these two rotation characteristics are completely different. The spatiotemporal hollow self-decelerating AELG wave packets can be attained if the mode numbers of the collinear AiELG wave packets are the same. Multi-ring structure evolves into single-ring structure along radial direction with their propagation distance increasing during propagation, which makes the hollow part expand continuously.-
Keywords:
- Airy-elegant-Laguerre-Gaussian beam /
- spatiotemporal self-decelerating wave packet /
- collinear propagation /
- hollow beam
[1] Berry M V, Balazs N L 1979 Am. J. Phys. 47 264
Google Scholar
[2] Siviloglou G A, Christodoulides D N 2007 Opt. Lett. 32 979
Google Scholar
[3] Siviloglou G A, Broky J, Dogariu A, Christodoulides D N 2007 Phys. Rev. Lett. 99 213
[4] Baumgartl J, Mazilu M, Dholakia K 2008 Nat. Photonics 2 675
Google Scholar
[5] Polynkin P, Kolesik M, Moloney J V, Siviloglou G A, Christodoulides D N 2009 Science 324 5924
[6] Chong A, Renninger W H, Christodoulides D N, Wise F W 2010 Nat. Photonics 4 103
Google Scholar
[7] Bandres M A, Gutiérrez-Vega J C 2007 Opt. Express 15 16719
Google Scholar
[8] Deng D M, Li H G 2012 Appl. Phys. B 106 677
Google Scholar
[9] Chen C D, Chen B, Peng X, Deng D M 2015 J. Opt. 17 035504
Google Scholar
[10] Zhang X P 2016 Opt. Commun. 367 364
Google Scholar
[11] Prabakaran K, Sangeetha P, Karthik V, Rajesh K B, Musthafa A M 2017 Chin. Phys. Lett. 34 054203
Google Scholar
[12] Malomed B A, Mihalache D, Wise F, Torner L 2005 J. Opt. B 7 R53
Google Scholar
[13] Mihalache D 2012 Rom. J. Phys. 57 352
[14] Valtna-Lukner H, Bowlan P, Löhmus M, Piksarv P, Trebino R, Saari P 2009 Opt. Express 17 14948
Google Scholar
[15] Abdollahpour D, Suntsov S, Papazoglou D G, Tzortzakis S 2010 Phys. Rev. Lett. 105 253901
Google Scholar
[16] Zhong W P, Belic M R, Huang T 2013 Phys. Rev. A 88 2974
[17] Zhong W P, Belic M, Zhang Y, Huang T 2014 Ann. Phys. 340 171
Google Scholar
[18] Zhong W P, Belic M, Zhang Y 2015 Opt. Express 23 23867
Google Scholar
[19] Zhong W P, Belic M, Zhang Y 2015 J. Phys. B 48 175401
Google Scholar
[20] Zhang X P 2017 Opt. Engineering 56 055102
Google Scholar
[21] Zhang X P 2017 J. Mod. Opt. 64 2035
Google Scholar
[22] Efremidis N K, Chen Z G, Segev M, Christodoulides D N 2019 Optica 6 686
Google Scholar
[23] Deng F, Deng D M 2016 Opt. Express 24 5478
Google Scholar
[24] Deng F, Zhang Z, Huang J, Deng D M 2016 JOSA B. 33 2204
Google Scholar
[25] Berry M V 2004 J. Opt. A, Pure Appl. Opt. 6 259
Google Scholar
[26] Lee W M, Yuan X C, Dholakia K 2004 Opt. Commun. 239 129
Google Scholar
[27] Leach J, Yao E, Padgett M J 2004 New J. Phys. 6 71
Google Scholar
[28] Arscott F M 1964 International 192 137
[29] Zhao F, Peng X, Zhang L P, Li D D, Zhuang J L, Chen X Y, Deng D M 2018 Laser Phys. 28 075001
Google Scholar
[30] Deng D M, Guo Q 2010 Appl. Phys. B 100 897
Google Scholar
[31] 张霞萍, 刘友文 2011 60 084212
Google Scholar
Zhang X P 2011 Acta Phys. Sin. 60 084212
Google Scholar
[32] Galvez E J, Smiley N, Fernandes N 2006 Proc. SPIE 6131 613105
Google Scholar
[33] Bekshaev A Y, Soskin M S, Vasnetsov M V 2006 Opt. Lett. 31 694
Google Scholar
[34] Zhao G W, Chen S J, Huang Z Z, Deng D M 2018 JOSA A. 35 1645
Google Scholar
[35] Chen S J, Zheng X Y, Zhan Y W, Ma S D, Deng D M 2019 Opt. Commun. 435 164
Google Scholar
-
图 1 不同初始入射速度的斜入射有限能量艾里光束的光场演化图 (a)
$ v_{0}=+3 $ ; (b)$ v_{0}=0 $ ; (c)$ v_{0} =-3$ ; (d) 图(c)的截面光强分布图Fig. 1. Intensity distribution of the Airy pulses with different initial incident velocity in free space: (a)
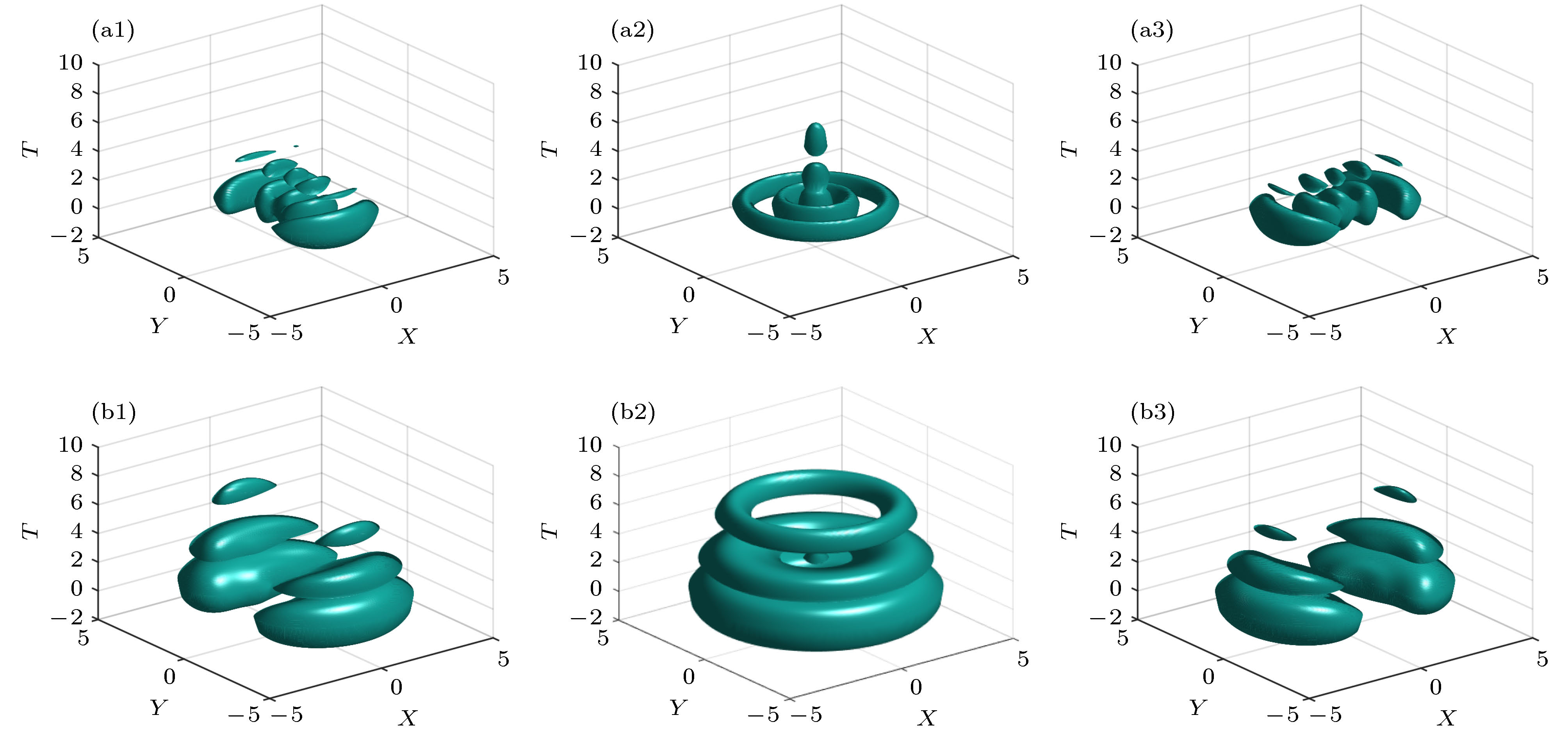
$ v_{0}=+3 $ ; (b)$ v_{0}=0 $ ; (c)$ v_{0}=-3 $ ; (d) the intensity profiles of the self-decelerating Airy pulses at different distances.
图 2 两束时空自减速AELG光束共线传输时随传输距离的面强度演化图 (a1), (b1) 传输距离
$ Z = 0 $ ; (a2), (b2) 传输距离$ Z = 0.5 $ ; (a3), (b3) 传输距离$ Z =1 $ . 双光束的模式指数分别为 (a1)—(a3)$ m_{2} =1 $ , (b1)—(b3)$ m_{2}=3 $ . 其他参数值分别为$ n_{1}=2, \;n_{2}=1,\; m_{1}=-1,\; \sigma=0, \;\theta= {\text{π}}/4 $ Fig. 2. Iso-surface intensity plots of self-decelerating collinear AELG wave packets at (a1), (b1)
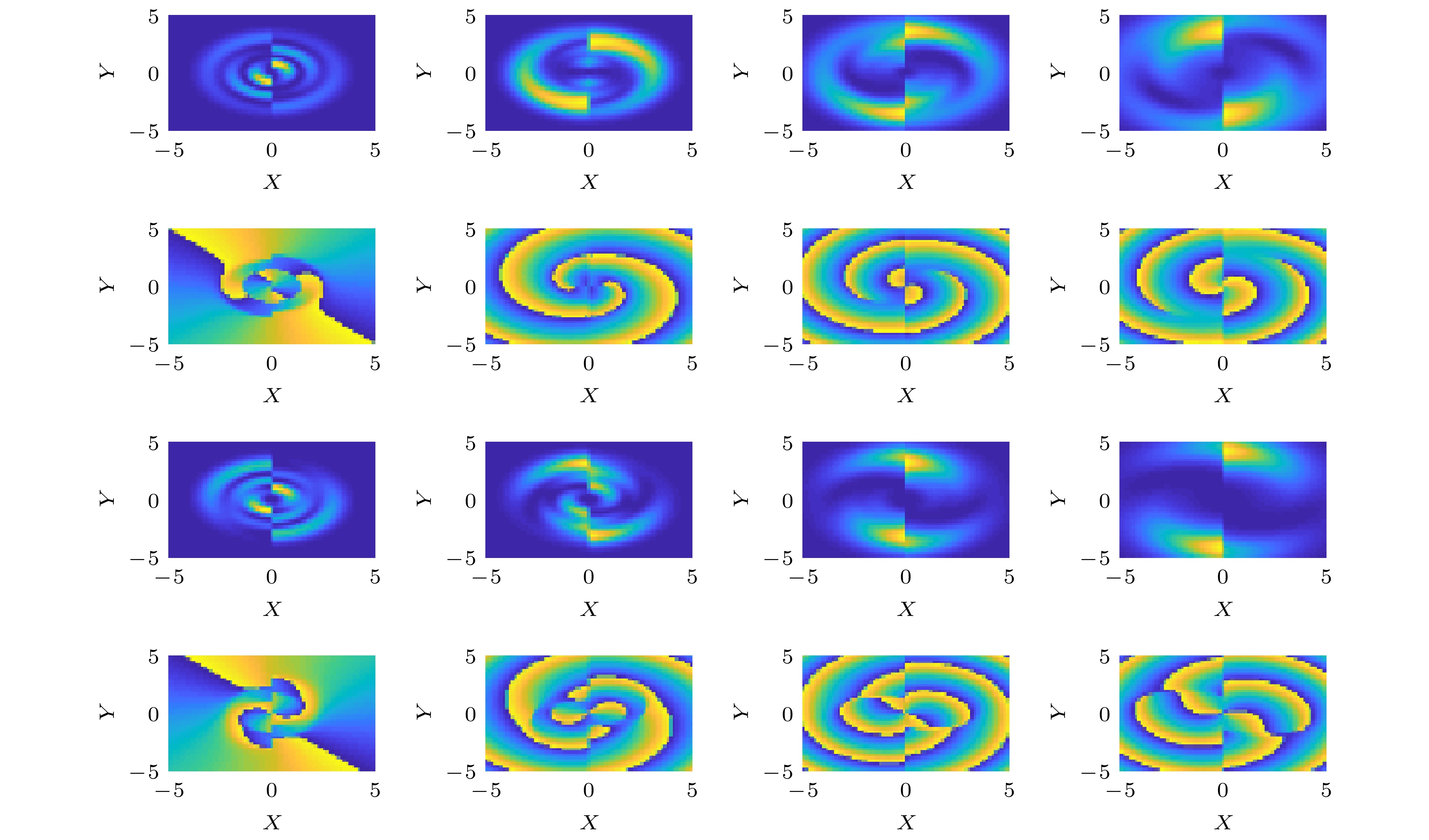
$ Z = 0 $ , (a2), (b2)$ Z = 0.5 $ , (a3), (b3)$ Z =1 $ . (a1)−(a3)$ m_{2} =1 $ , (b1)−(b3)$ m_{2}=3 $ . Other parameters are chosen as$ n_{1}=2,\; n_{2}=1,\; m_{1}=-1, \;\sigma=0,\; \theta= {\text{π}}/4 $ 
图 3 两束自减速时空AELG光束共线传输时传输截面的强度和相位分布图 第一行和第二行相对应模式指数为
$ m_{2} =1 $ , 第三行和第四行相对于$ m_{2} =3 $ . 第一行和第三行为强度分布图, 第二行和第四行为相位分布图, 其中第四行对应于传输距离为$ Z=1.5 $ .$ T=0 $ , 其他参数的选择同图2Fig. 3. The intensity and phase distributions of the self-decelerating collinear AELG wave packets at the profile during propagation. the first and second rows correspond to
$ m_{2} =1 $ , and the third and forth rows correspond to$ m_{2} =3 $ . The first and third rows show the intensity distribution, and the second and forth rows show the phase distribution. the forth column corresponds to$ Z=1.5 $ . Other parameters are the same as Fig. 2 except$ T=0 $ 
图 4 两束自减速时空AELG光束共线传输不同权重时的面强度演化图 (a1)−(a3) 传输距离
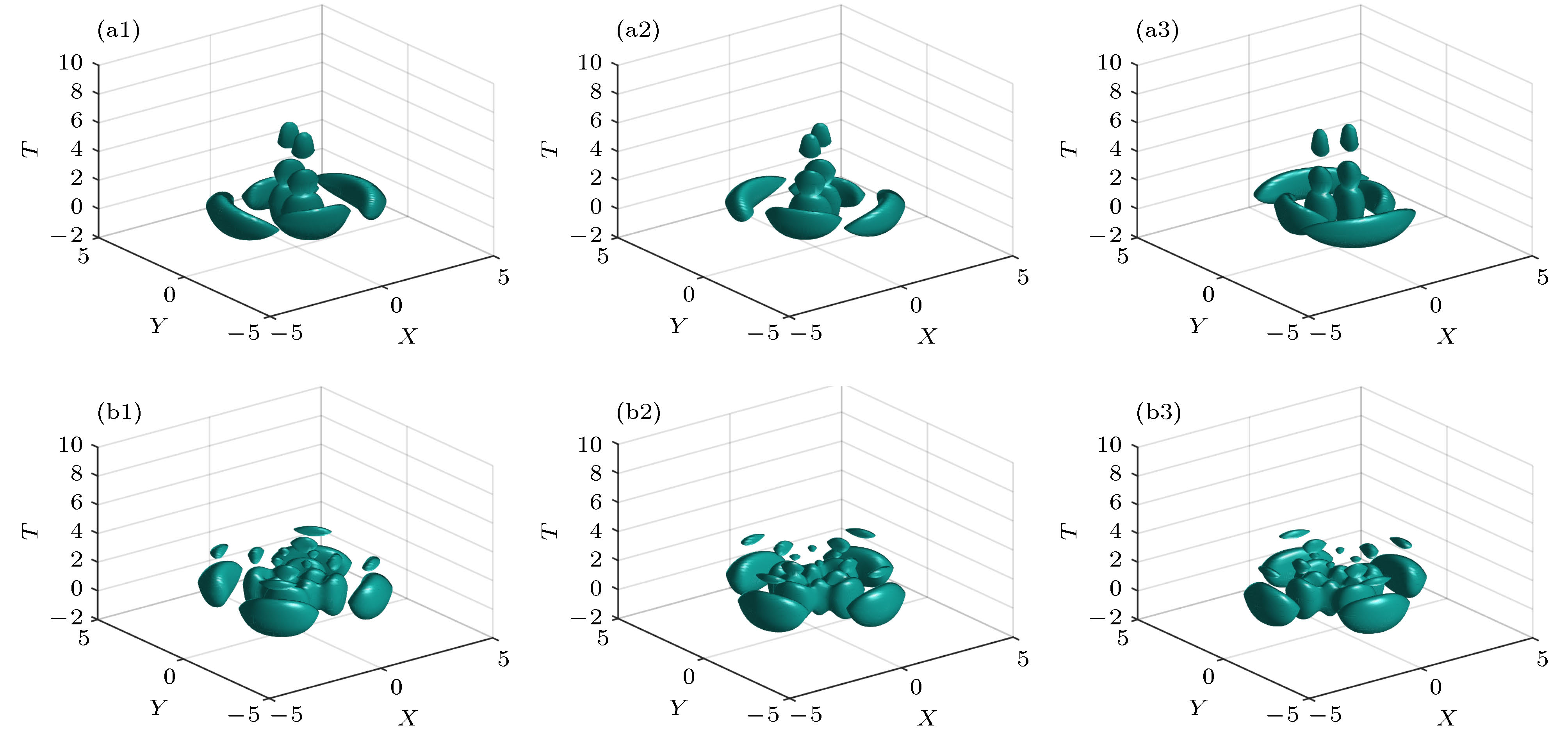
$ Z = 0 $ ; (b1)−(b3)传输距离$ Z=1 $ . (a1), (b1) 对应于权重为$ \theta={\text{π}}/4 $ ; (a2), (b2) 对应于权重为$ \theta={\text{π}}/2 $ ; (a3), (b3)对应于权重为$ \theta=3{\text{π}}/4 $ . 其他的参数值分别是$ n_{1}=2,\;n_{2}=1,\;m1=0, \; m_{2}=-2, \sigma=0 $ Fig. 4. Iso-surface intensity plots of self-decelerating collinear AELG wave packets at (a1)−(a3)
$ Z = 0 $ ; (b1)−(b3)$ Z=1 $ . (a1), (b1)$ \theta={\text{π}}/4 $ ; (a2), (b2)$ \theta={\text{π}}/2 $ ; (a3), (b3)$ \theta=3{\text{π}}/4 $ .Other parameters are chosen as$ n_{1}=2,\; n_{2}=1,\; m1=0, \;m_{2}=-2,\;\sigma=0 $ 
图 5 两束自减速时空AELG光束共线传输不同初始相位差时的面强度演化图 (a1)−(a3)模式指数为
$ m_{2}=1 $ ; (b1)−(b3)模式指数为$ m_{2}=3 $ . 其中 (a1), (b1) 对应于初始相位差$ \sigma=0 $ ; (a2), (b2) 对应于$ \sigma={\text{π}}/2 $ ; (a3), (b3)对应于$ \sigma={\text{π}} $ . 其他参数值分别为$ n_{1}=2,\; n_{2}=1, \;m_{1}=-1, \;\theta={\text{π}}/4 $ Fig. 5. Iso-surface intensity plots of self-decelerating collinear AELG wave packets at (a1)−(a3)
$ m_{2}=1 $ ; (b1)−(b3)$ m_{2}=3 $ . (a1), (b1)$ \sigma={\text{π}}/4 $ ; (a2), (b2)$ \sigma={\text{π}}/2 $ ; (a3), (b3)$ \sigma={\text{π}} $ . Other parameters are chosen as$ n_{1}=2,\; n_{2}=1,\; m_{1}=-1,\; m_{2}=1, \;\theta={\text{π}}/4$ 
图 6 两束自减速时空AELG光束共线传输时产生中空时空光束 (a1)−(a3) 模式指数为m1 = m2 = 1, n1 = 4, n2 = 2; (b1)−(b3)模式指数为
$ m_{1}=m_{2}=-1,\; n_{1}=n_{2}=4 $ . 其截面上的光强分布对应于第三行. 其中$ \sigma={\text{π}}/4 $ ,$ \theta={\text{π}}/4 $ Fig. 6. The hollow Self-decelerating AELG wave packets. The first row corresponds to
$ m_{1}=m_{2}=1, n_{1}=4, n_{2}=2 $ , and the second row is$ m_{1}=m_{2}=-1, \;n_{1}=n_{2}=4 $ . The third row is the distribution of intensity corresponding to the second row at the section during propagation. Other parameters are$ \sigma={\text{π}}/4 $ ,$ \theta={\text{π}}/4 $ -
[1] Berry M V, Balazs N L 1979 Am. J. Phys. 47 264
Google Scholar
[2] Siviloglou G A, Christodoulides D N 2007 Opt. Lett. 32 979
Google Scholar
[3] Siviloglou G A, Broky J, Dogariu A, Christodoulides D N 2007 Phys. Rev. Lett. 99 213
[4] Baumgartl J, Mazilu M, Dholakia K 2008 Nat. Photonics 2 675
Google Scholar
[5] Polynkin P, Kolesik M, Moloney J V, Siviloglou G A, Christodoulides D N 2009 Science 324 5924
[6] Chong A, Renninger W H, Christodoulides D N, Wise F W 2010 Nat. Photonics 4 103
Google Scholar
[7] Bandres M A, Gutiérrez-Vega J C 2007 Opt. Express 15 16719
Google Scholar
[8] Deng D M, Li H G 2012 Appl. Phys. B 106 677
Google Scholar
[9] Chen C D, Chen B, Peng X, Deng D M 2015 J. Opt. 17 035504
Google Scholar
[10] Zhang X P 2016 Opt. Commun. 367 364
Google Scholar
[11] Prabakaran K, Sangeetha P, Karthik V, Rajesh K B, Musthafa A M 2017 Chin. Phys. Lett. 34 054203
Google Scholar
[12] Malomed B A, Mihalache D, Wise F, Torner L 2005 J. Opt. B 7 R53
Google Scholar
[13] Mihalache D 2012 Rom. J. Phys. 57 352
[14] Valtna-Lukner H, Bowlan P, Löhmus M, Piksarv P, Trebino R, Saari P 2009 Opt. Express 17 14948
Google Scholar
[15] Abdollahpour D, Suntsov S, Papazoglou D G, Tzortzakis S 2010 Phys. Rev. Lett. 105 253901
Google Scholar
[16] Zhong W P, Belic M R, Huang T 2013 Phys. Rev. A 88 2974
[17] Zhong W P, Belic M, Zhang Y, Huang T 2014 Ann. Phys. 340 171
Google Scholar
[18] Zhong W P, Belic M, Zhang Y 2015 Opt. Express 23 23867
Google Scholar
[19] Zhong W P, Belic M, Zhang Y 2015 J. Phys. B 48 175401
Google Scholar
[20] Zhang X P 2017 Opt. Engineering 56 055102
Google Scholar
[21] Zhang X P 2017 J. Mod. Opt. 64 2035
Google Scholar
[22] Efremidis N K, Chen Z G, Segev M, Christodoulides D N 2019 Optica 6 686
Google Scholar
[23] Deng F, Deng D M 2016 Opt. Express 24 5478
Google Scholar
[24] Deng F, Zhang Z, Huang J, Deng D M 2016 JOSA B. 33 2204
Google Scholar
[25] Berry M V 2004 J. Opt. A, Pure Appl. Opt. 6 259
Google Scholar
[26] Lee W M, Yuan X C, Dholakia K 2004 Opt. Commun. 239 129
Google Scholar
[27] Leach J, Yao E, Padgett M J 2004 New J. Phys. 6 71
Google Scholar
[28] Arscott F M 1964 International 192 137
[29] Zhao F, Peng X, Zhang L P, Li D D, Zhuang J L, Chen X Y, Deng D M 2018 Laser Phys. 28 075001
Google Scholar
[30] Deng D M, Guo Q 2010 Appl. Phys. B 100 897
Google Scholar
[31] 张霞萍, 刘友文 2011 60 084212
Google Scholar
Zhang X P 2011 Acta Phys. Sin. 60 084212
Google Scholar
[32] Galvez E J, Smiley N, Fernandes N 2006 Proc. SPIE 6131 613105
Google Scholar
[33] Bekshaev A Y, Soskin M S, Vasnetsov M V 2006 Opt. Lett. 31 694
Google Scholar
[34] Zhao G W, Chen S J, Huang Z Z, Deng D M 2018 JOSA A. 35 1645
Google Scholar
[35] Chen S J, Zheng X Y, Zhan Y W, Ma S D, Deng D M 2019 Opt. Commun. 435 164
Google Scholar
下载:
计量
- 文章访问数: 7899
- PDF下载量: 96
- 被引次数: 0
