-
本文研究了旋磁铁氧体材料在不同条件下(磁化状态, 大块材料和离散的阵列形式)对低频电磁波的吸收性能以及铁氧体基元间的耦合作用对吸收带宽的影响. 研究结果表明, 通过旋磁铁氧体在吸波材料中的结构设计可以实现对低频电磁波的高效吸收. 文中4 mm大块薄层旋磁铁氧体反射率的–10 dB频点能低至0.48 GHz, 并可以通过调整偏置磁场的大小或者离散铁氧体基元的大小灵活地改变共振频率. 引入不同尺寸的基元形成的多谐振峰及其相互的耦合可以有效拓展–10 dB带宽, 并且这种展宽作用在不同的磁化状态下都是有效的. 当采用横向偏置场700 Oe时, 两基元吸波材料–10 dB带宽可达单个基元各自作用带宽之和的105.7%.Under the action of static bias magnetic field, the magnetized ferrite has a permeability tensor which can be adjusted by the applied magnetic field. In this paper, the absorption properties of bulk gyromagnetic ferrites under different magnetized conditions are studied and the great potential of gyromagnetic ferrite in achieving low frequency electromagnetic wave absorption is demonstrated. Full wave electromagnetic simulations are performed based on the finite element method (FEM). A floquet port is adopted at the top boundary of the unit cell to simulate a normally incident plane wave. The unit cell boundary conditions are used in the x-y plane to simulate a periodic structure. Orthogonality magnetization in plane is utilized to solve the polarization selectivity in the condition of transverse magnetic field. The influence on absorption capacity of discrete ferrite array structure and the coupling effect of ferrite elements with different sizes are also studied in consideration of the size effect. The simulation results show that a thin bulk gyromagnetic ferrite layer whose thickness is only 4 mm can possess frequency as low as 0.48 GHz and reflectivity below –10 dB. Gyromagnetic ferrite presents different absorption properties under longitudinal magnetization and transversal magnetization, and different polarization directions in transversal magnetization as well. When longitudinal bias magnetic field H0 = 200 Oe, the bandwidth of the reflectivity below –10 dB ranges from 0.48 to 1.84 GHz. The resonant absorption frequency can be regulated by adjusting bias magnetic field and the size of ferrite element. In general, a large bias magnetic field leads to a high resonant frequency due to the ferromagnetic resonance frequency positively associated with the applied magnetic field, but a ferrite array consisting of larger size elements provides a lower resonant frequency for the size resonance negatively associated with the size. By introducing the coupling between elements with different sizes, the reflection bandwidth below –10 dB can be effectively extended to above 80% of the sum of the bandwidth possessed by single unit cell, especially 105.7% under transversal bias magnetic field 700 Oe. And the broadening effect is effective in both longitudinal and transverse magnetized state but it will be weaker when the two absorption peaks are closer. To further understand the absorption mechanism of the two-element absorber, the distribution of the electric field, magnetic field and power loss density are examined. The results prove that the two peaks at the lower frequency exactly originates from
$ \Delta R = 0$ and the higher frequency originates from$ \Delta R = 4$ , and therefore the widened absorption is contributed by the coupled multiple resonances provided by the elements with different sizes.[1] Landy N I, Sajuyigbe S, Mock J J, Smith D R, Padilla W J 2008 Phys. Rev. Lett. 100 207402
Google Scholar
[2] Ding F, Cui Y X, Ge X C, Jin Y, He S L 2012 Appl. Phys. Lett. 100 103506
Google Scholar
[3] Zhang Y, Huang Y, Zhang T F, Chang H C, Xiao P S, Chen H H, Huang Z Y, Chen Y S 2015 Adv. Mater. 27 2049
Google Scholar
[4] Wang Y, Du Y C, Xu P, Qiang R, Han X J 2017 Polymers 9 29
Google Scholar
[5] Liu Y P, Zhang B Z, Duan J P, Xu Y G 2018 Appl. Opt. 57 10257
Google Scholar
[6] Zhang X J, Wang G S, Cao W Q, Wei Y Z, Liang J F, Guo L, Cao M S 2014 ACS Appl. Mater. Interfaces 6 7471
Google Scholar
[7] Zhang Y, Huang Y, Chen H H, Huang Z Y, Yang Y, Xiao P S, Zhou Y, Chen Y S 2016 Carbon 105 438
Google Scholar
[8] Wang D J, Zhang J Y, He P, Hou Z L 2019 Ceram. Int. 45 23043
Google Scholar
[9] 周卓辉, 刘晓来, 黄大庆, 康飞宇 2014 63 184101
Google Scholar
Zhou Z H, Liu X L, Huang D Q, Kang F Y 2014 Acta Phys. Sin. 63 184101
Google Scholar
[10] Zhang K L, Zhang J Y, Hou Z L, Bi S, Zhao Q L 2019 Carbon 141 608
Google Scholar
[11] Wang J, Gao C N, Jiang Y N, Charles N A 2017 Chin. Phys. B 26 114102
Google Scholar
[12] Wang Y, Du Y C, Qiang R, Tian C H, Xu P, Han X J 2016 Adv. Mater. Interfaces 3 1500684
Google Scholar
[13] Alkuh M S, Famili M H N, Shirvan M M M, Moeini M H 2016 Mater. Des. 100 73
Google Scholar
[14] Amano M, Kotsuka Y 2003 IEEE Trans. Microwave Theory Tech. 51 238
Google Scholar
[15] Kazantsev Y N, Lopatin A V, Kazantseva N E, Shatrov A D, Mal'tsev V P, Vilcakova J, Saha P 2010 IEEE Trans. Antennas Propag. 58 1227
Google Scholar
[16] Chen H Y, Zhang H B, Deng L J 2010 IEEE Antennas Wirel. Propag. Lett. 9 899
Google Scholar
[17] Rozanov K N, Li Z W, Chen L F, Koledintseva M Y 2005 J. Appl. Phys. 97 013905
[18] Park M J, Choi J H, Kim S S 2000 Intermag Proceedings of International Magnetics Conference Toronto, Canada, April 09−12, 2000 p3272
[19] Jacobo S E, Fano W G, Razzitte A C, Digiovanni N D, Trainotti V 1998 Proceedings of the 67th Annual Conference on Electrical Insulation and Dielectric Phenomena Atlanta, USA, October 25−28, 1998 p273
[20] Bi K, Guo Y S, Liu X M, Zhao Q, Xiao J H, Lei M, Zhou J 2014 Sci. Rep. 4 7001
[21] Yang Y J, Huang Y J, Wen G J, Zhong J P, Sun H B, Oghenemuero G 2012 Chin. Phys. B 21 038501
Google Scholar
[22] 郭飞, 杜红亮, 屈绍波, 夏颂, 徐卓, 赵建峰, 张红梅 2015 64 077801
Google Scholar
Guo F, Du H L, Qu S B, Xia S, Xu Z, Zhao J F, Zhang H M 2015 Acta Phys. Sin. 64 077801
Google Scholar
[23] Meena R S, Bhattachrya S, Chatterjee R 2010 J. Magn. Magn. Mater. 322 1923
Google Scholar
[24] Liu X S, Hernandez-Gomez P, Huang K, Zhou S Q, Wang Y, Cai X, Sun H J, Ma B 2006 J. Magn. Magn. Mater. 305 524
Google Scholar
[25] Bercoff P G, Herme C, Jacobo S E 2009 J. Magn. Magn. Mater. 321 2245
Google Scholar
[26] Zuo X, How H, Somu S, Vittoria C 2003 IEEE Trans. Magn. 39 3160
Google Scholar
[27] Pozar D M 2004 Microwave Engineering (3rd ed) (New York: Wiely) pp391−395
[28] Yang Y, Yang Y, Wen X, Ding J 2014 J. Appl. Phys. 115 17A521
Google Scholar
[29] Zhang K L, Hou Z L, Bi S, Fang H M 2017 Chin. Phys. B 26 127802
Google Scholar
-
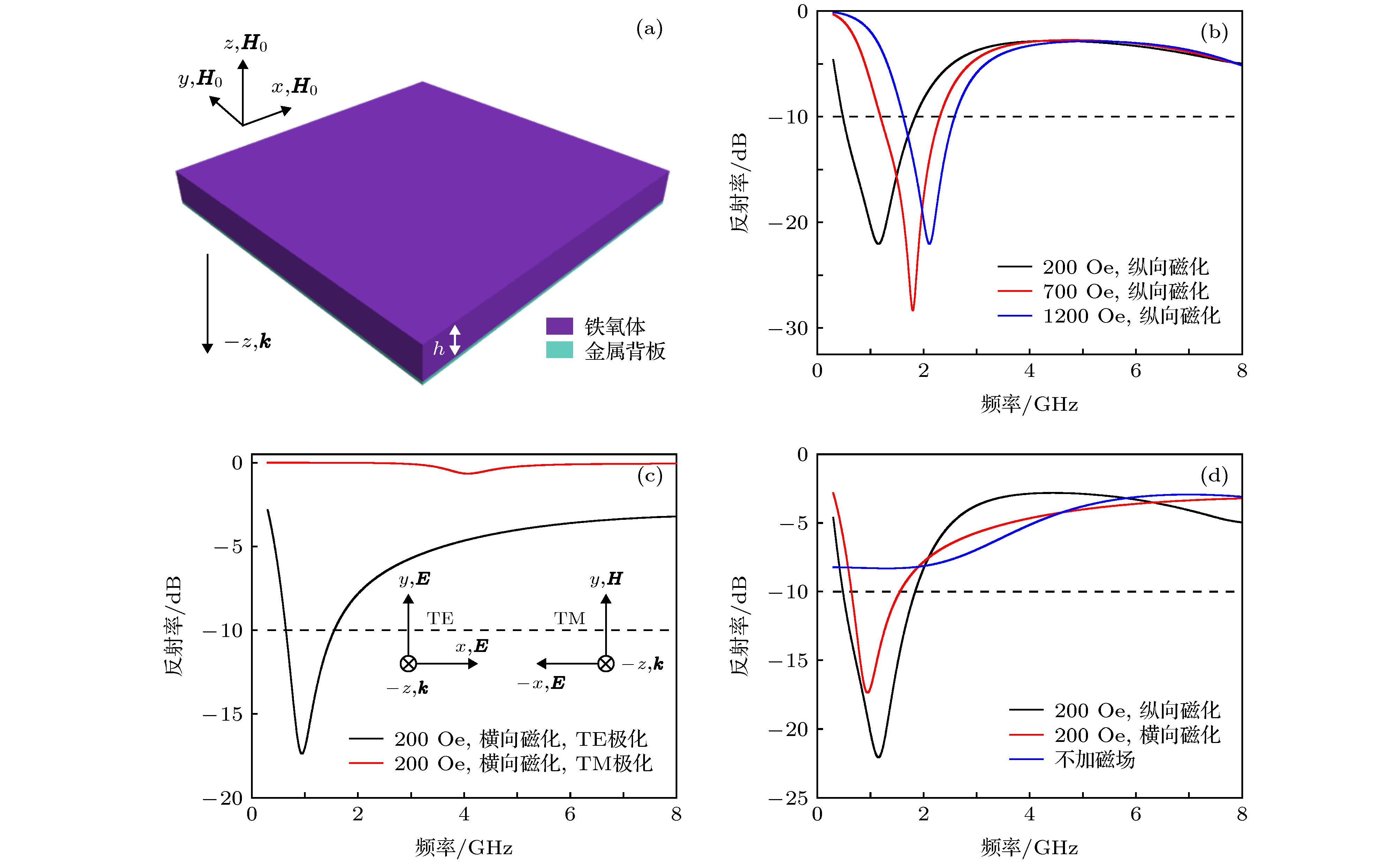
图 1 大块铁氧体模型示意图和在不同磁化方式、磁场强度、极化方向下对电磁波的反射率 (a)模型示意图; (b)纵向磁化下不同磁场强度对反射率的影响; (c)横向磁化下不同极化方向的反射率; (d)不同磁化方式对反射率的影响
Fig. 1. The schematic model and the reflectivity of bulk ferrite under different magnetized methods, magnetic field intensities and polarized directions: (a) The schematic model; (b) the influence of different magnetic field intensities under longitudinal magnetization; (c) different polarized directions under transversal magnetization; (d) the influence of different magnetized methods.
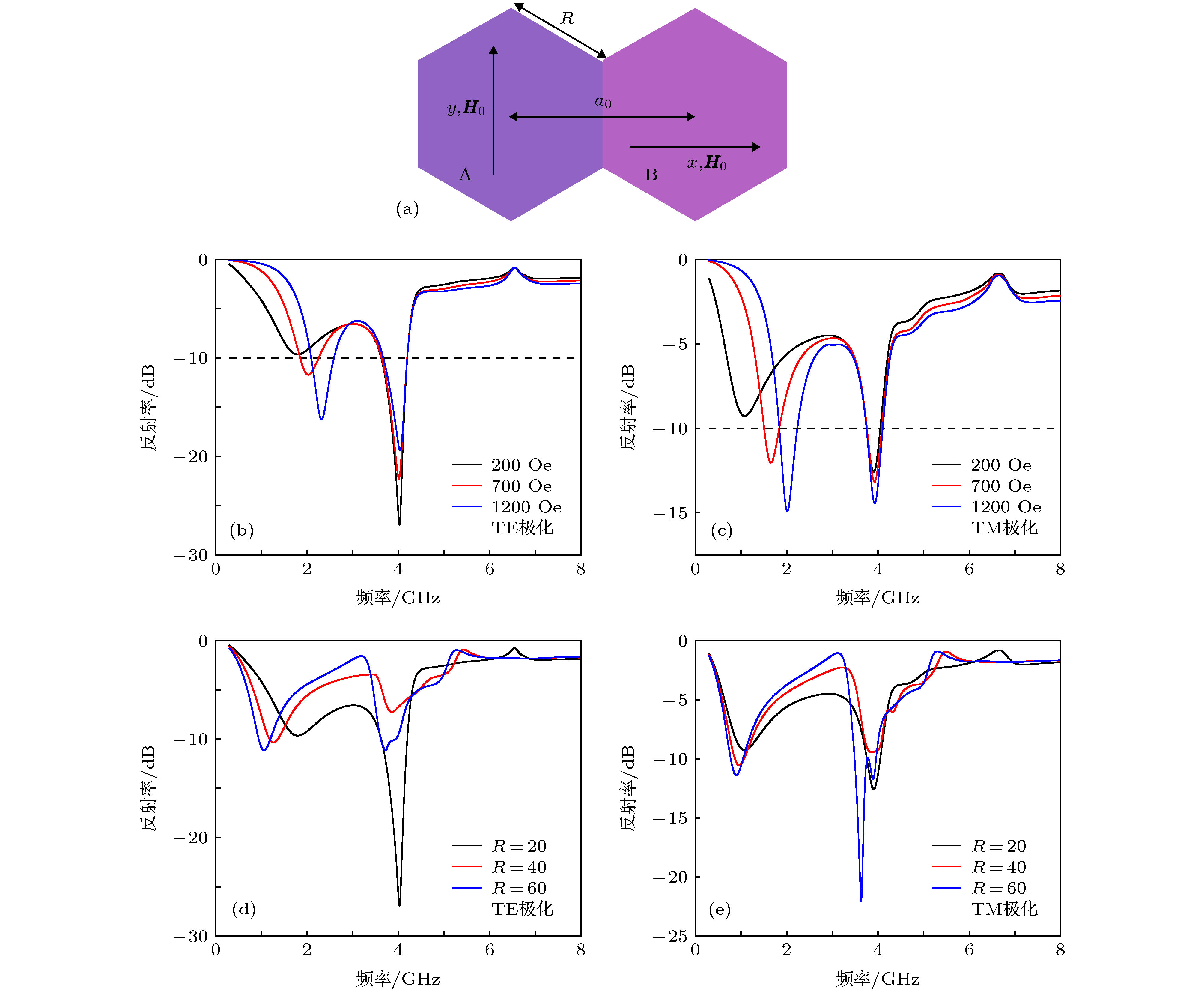
图 2 基元结构和横向磁化时面内正交磁化作用下铁氧体的反射率 (a)基元结构(A, B分别表示沿y向磁化和x向磁化的铁氧体基元); (b) TE极化; (c) TM极化; (d) TE极化时尺寸效应; (e) TM极化时尺寸效应
Fig. 2. The unit cell and the reflectivity of transversally orthogonally magnetized ferrite: (a) The unit cell(A and B present the ferrite magnetized along y and x directions, respectively); the reflectivity of (b) TE polarization and (c) TM polarization; the size effect of (d) TE polarization and (e) TM polarization.
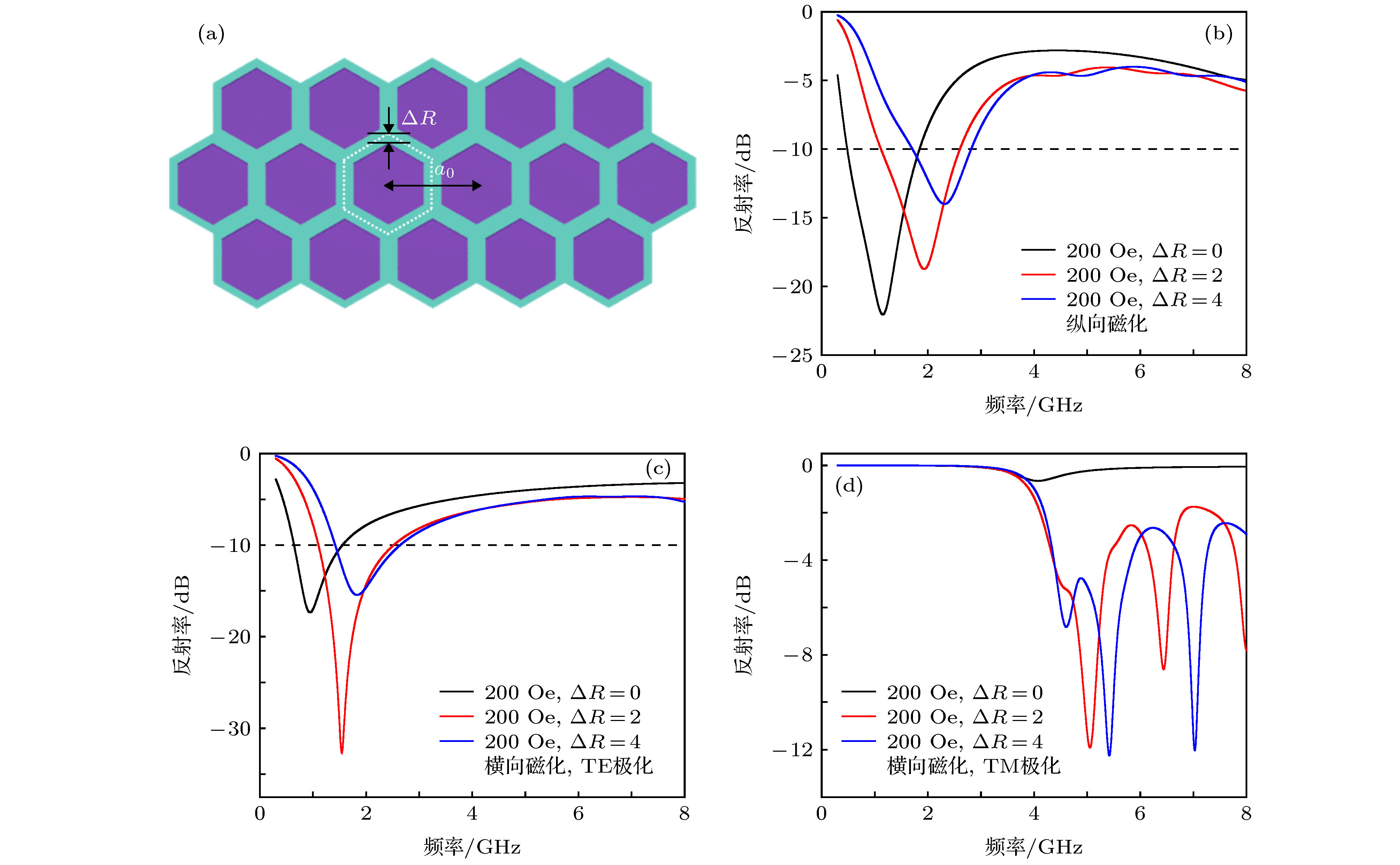
图 3 不同基元大小的铁氧体阵列及其在不同磁化状态下的反射性能 (a)离散的铁氧体阵列; (b)纵向磁化下
$\Delta R$ 的影响; (c)横向磁化TE极化下$\Delta R$ 的影响; (d)横向磁化TM极化下$\Delta R$ 的影响Fig. 3. Reflection of ferrites array with different element sizes in different magnetized conditions: (a) The discrete array; the influence of
$\Delta R$ in (b) longitudinal magnetization; (c) transversal magnetization with TE polarization and (d) transverse magnetization with TM polarization.
图 4 结构示意图和不同尺寸基元组合的性能 (a)结构示意图(左部分表示超胞1(2)的细节); (b)纵向磁化200 Oe,
$\Delta R = 0$ 和$\Delta R = 4$ 组合; (c)纵向磁化700 Oe,$\Delta R = 0$ 和$\Delta R = 4$ 组合; (d)纵向磁化700 Oe,$\Delta R = 0$ 和$\Delta R = 2$ 组合; (e)横向磁化200 Oe,$\Delta R = 0$ 和$\Delta R = 4$ 组合; (f)横向磁化700 Oe,$\Delta R = 0$ 和$\Delta R = 4$ 组合; (g)横向磁化700 Oe,$\Delta R = 0$ 和$\Delta R = 2$ 组合Fig. 4. The schematic and the properties of elements combinations with different sizes: (a) Schematic of the array combined by different elements(The left shows the details of supercell1(2)); the combination of
$\Delta R = 0$ and$\Delta R = 4$ under longitudinal magnetization (b) 200 Oe and (c) 700 Oe; (d) the combination of$\Delta R = 0$ and$\Delta R = 2$ under longitudinal magnetization 700 Oe; the combination of$\Delta R = 0$ and$\Delta R = 4$ under transversal magnetization (e) 200 Oe and (f) 700 Oe; (g) the combination of$\Delta R = 0$ and$\Delta R = 2$ under transversal magnetization 700 Oe.
图 5 由
$\Delta R = 0$ 与$\Delta R = 4$ 两种阵列组合而成的吸波结构在y = 0平面内的电场, 磁场, 能量损耗密度分布 (a), (b)分别为工作频率1.95和3.05 GHz, 纵向磁化场700 Oe时的情形; (c), (d)分别是工作频率为1.65和2.25 GHz, 横向磁化场700 Oe时的情形Fig. 5. Distributions of electric field, magnetic field and power loss density in the y = 0 plane of the absorption structure combined by
$\Delta R = 0$ and$\Delta R = 4$ at two absorption peaks: (a) 1.95 GHz and (b) 3.05 GHz of longitudinal magnetization 700 Oe; (c) 1.65 GHz and (d) 2.25 GHz of transversal magnetization 700 Oe.
图 6 能量损耗密度在x-y截面(正视图)的分布 (a), (b)分别是工作频率为1.95和3.05 GHz, 纵向磁化磁场700 Oe时的情形; (c), (d)分别是工作频率为1.65和2.25 GHz时, 横向磁化场700 Oe时的情形
Fig. 6. Distributions of power loss density in the x-y cross section (the front view): (a) 1.95 GHz and (b) 3.05 GHz of longitudinal magnetization 700 Oe; (c) 1.65 GHz and (d) 2.25 GHz of transversal magnetization 700 Oe.
-
[1] Landy N I, Sajuyigbe S, Mock J J, Smith D R, Padilla W J 2008 Phys. Rev. Lett. 100 207402
Google Scholar
[2] Ding F, Cui Y X, Ge X C, Jin Y, He S L 2012 Appl. Phys. Lett. 100 103506
Google Scholar
[3] Zhang Y, Huang Y, Zhang T F, Chang H C, Xiao P S, Chen H H, Huang Z Y, Chen Y S 2015 Adv. Mater. 27 2049
Google Scholar
[4] Wang Y, Du Y C, Xu P, Qiang R, Han X J 2017 Polymers 9 29
Google Scholar
[5] Liu Y P, Zhang B Z, Duan J P, Xu Y G 2018 Appl. Opt. 57 10257
Google Scholar
[6] Zhang X J, Wang G S, Cao W Q, Wei Y Z, Liang J F, Guo L, Cao M S 2014 ACS Appl. Mater. Interfaces 6 7471
Google Scholar
[7] Zhang Y, Huang Y, Chen H H, Huang Z Y, Yang Y, Xiao P S, Zhou Y, Chen Y S 2016 Carbon 105 438
Google Scholar
[8] Wang D J, Zhang J Y, He P, Hou Z L 2019 Ceram. Int. 45 23043
Google Scholar
[9] 周卓辉, 刘晓来, 黄大庆, 康飞宇 2014 63 184101
Google Scholar
Zhou Z H, Liu X L, Huang D Q, Kang F Y 2014 Acta Phys. Sin. 63 184101
Google Scholar
[10] Zhang K L, Zhang J Y, Hou Z L, Bi S, Zhao Q L 2019 Carbon 141 608
Google Scholar
[11] Wang J, Gao C N, Jiang Y N, Charles N A 2017 Chin. Phys. B 26 114102
Google Scholar
[12] Wang Y, Du Y C, Qiang R, Tian C H, Xu P, Han X J 2016 Adv. Mater. Interfaces 3 1500684
Google Scholar
[13] Alkuh M S, Famili M H N, Shirvan M M M, Moeini M H 2016 Mater. Des. 100 73
Google Scholar
[14] Amano M, Kotsuka Y 2003 IEEE Trans. Microwave Theory Tech. 51 238
Google Scholar
[15] Kazantsev Y N, Lopatin A V, Kazantseva N E, Shatrov A D, Mal'tsev V P, Vilcakova J, Saha P 2010 IEEE Trans. Antennas Propag. 58 1227
Google Scholar
[16] Chen H Y, Zhang H B, Deng L J 2010 IEEE Antennas Wirel. Propag. Lett. 9 899
Google Scholar
[17] Rozanov K N, Li Z W, Chen L F, Koledintseva M Y 2005 J. Appl. Phys. 97 013905
[18] Park M J, Choi J H, Kim S S 2000 Intermag Proceedings of International Magnetics Conference Toronto, Canada, April 09−12, 2000 p3272
[19] Jacobo S E, Fano W G, Razzitte A C, Digiovanni N D, Trainotti V 1998 Proceedings of the 67th Annual Conference on Electrical Insulation and Dielectric Phenomena Atlanta, USA, October 25−28, 1998 p273
[20] Bi K, Guo Y S, Liu X M, Zhao Q, Xiao J H, Lei M, Zhou J 2014 Sci. Rep. 4 7001
[21] Yang Y J, Huang Y J, Wen G J, Zhong J P, Sun H B, Oghenemuero G 2012 Chin. Phys. B 21 038501
Google Scholar
[22] 郭飞, 杜红亮, 屈绍波, 夏颂, 徐卓, 赵建峰, 张红梅 2015 64 077801
Google Scholar
Guo F, Du H L, Qu S B, Xia S, Xu Z, Zhao J F, Zhang H M 2015 Acta Phys. Sin. 64 077801
Google Scholar
[23] Meena R S, Bhattachrya S, Chatterjee R 2010 J. Magn. Magn. Mater. 322 1923
Google Scholar
[24] Liu X S, Hernandez-Gomez P, Huang K, Zhou S Q, Wang Y, Cai X, Sun H J, Ma B 2006 J. Magn. Magn. Mater. 305 524
Google Scholar
[25] Bercoff P G, Herme C, Jacobo S E 2009 J. Magn. Magn. Mater. 321 2245
Google Scholar
[26] Zuo X, How H, Somu S, Vittoria C 2003 IEEE Trans. Magn. 39 3160
Google Scholar
[27] Pozar D M 2004 Microwave Engineering (3rd ed) (New York: Wiely) pp391−395
[28] Yang Y, Yang Y, Wen X, Ding J 2014 J. Appl. Phys. 115 17A521
Google Scholar
[29] Zhang K L, Hou Z L, Bi S, Fang H M 2017 Chin. Phys. B 26 127802
Google Scholar
下载:
计量
- 文章访问数: 10283
- PDF下载量: 214
- 被引次数: 0
