层状铁磁体Fe<sub>0.26</sub>TaS<sub>2</sub>的Andreev反射谱

于晓洋; 冯红磊; 辜刚旭; 刘永河; 李治林; 徐同帅; 李永庆

doi:10.7498/aps.68.20191221

摘要

如何避免界面反应、可靠地提取材料的自旋极化率是自旋电子学的一个基本问题. 本文选取了一种独特的铁磁性层状过渡族金属硫化物Fe_0.26TaS₂, 研究了单晶材料的磁性、电子输运和Andreev反射谱. 磁性和输运结果表明, 低温下Fe_0.26TaS₂单晶存在强磁各向异性、双峰磁电阻和反常霍尔效应. 通过干法转移方案制备的干净界面的Fe_0.26TaS₂超导异质结的Andreev反射谱, 发现该材料的自旋极化率为47% ± 7%. 本文展示的干法转移制备超导/磁性异质结的方法可广泛用于测量各种二维磁性材料的自旋极化率.

关键词:

Abstract

An elementary mission of spintronics research is to prevent the interface reacting in spin device and extract spin polarization of ferromagnetic material reliably. Layered transition metal sulfide has very strong anisotropic magnetism, magnetoresistance, and unique Hall effect. It provides a good platform for studying the magnetic order related physical phenomena and may lay a foundation for spintronic applications. In this work, the magnetism, electronic transport and Andreev reflection spectrum of a novel ferromagnetic material Fe_0.26TaS₂ with a layers-stacked structure are measured. Strong magnetic anisotropy, double-peak magnetoresistance and anomalous Hall effect are found. In the magnetic measurement, the strong magnetic anisotropy behavior in Fe_0.26TaS₂ single crystal is observed. Curie temperature T_C of the Fe_0.26TaS₂ single crystal is confirmed by zero field cooling, field cooling and Arrot plot. The electronic transport in the Fe_0.26TaS₂ single crystal also reveals strong anisotropic behaviors, such as butterfly-like magnetoresistance and obvious anomalous hall effect below T_C.To obtain the spin polarization of Fe_xTaS₂, we fabricate an Fe_xTaS₂/superconductor Andreev junction to measure the spin polarization that is fitted by the modified Blonder-Tinkham-Klapwijk (BTK) theory. Perhaps the diffusion of Pb can form an alloy structure, creating another superconductor behavior. The two-gap BTK theory confirms our hypothesis, and the result spin polarization can reach 26%. To avoid the interference from Pb alloy superconductor, we also fabricate an Fe_0.26TaS₂/Al/Pb superconductor junction by evaporating Al and then Pb film on the surface of Fe_0.26TaS₂ in sequence. The results of BTK fit show that the spin polarization from the first technical route cannot be reliable due to the tunneling layer on the Al interface. In order to obtain a clean interface, Fe_0.26TaS₂/NbSe₂ junction is fabricated through mechanical-exfoliation and dry-transfer method. Through the Andreev reflection spectrum of this junction, the spin polarization of Fe_0.26TaS₂ is extracted to be 47% ± 7%. For various two-dimensional ferromagnetic materials, our work suggests that the dry-transfer method is well applicable in spin polarization extraction. The results of spin polarization indicate that the Fe_0.26TaS₂ is a promising candidate of next-generation material of spintronics.

Keywords:

作者及机构信息

1.
中国科学院物理研究所, 北京　100190

2.
中国科学院大学物理科学学院, 北京　100049

3.
安阳师范学院物理与电气工程学院, 安阳　455000

4.
北京大学物理学院, 北京　100871

通信作者: 徐同帅, xutongshuai@iphy.ac.cn

基金项目: 国家自然科学基金(批准号: 61425015, 11704006)、中国科学院B类战略性先导科技专项(批准号: XDB28000000)和国家重点研发计划(批准号: 2016YFA0300600)资助的课题

Authors and contacts

1.
Institute of Physics, Chinese Academy of Sciences, Beijing 100190, China

2.
School of Physical Sciences, University of Chinese Academy of Sciences, Beijing 100049, China

3.
School of Physics and Electrical Engineering, Anyang Normal University, Anyang 455000, China

4.
School of Physical Sciences, Peking University, Beijing 100871, China

Corresponding author: Xu Tong-Shuai, xutongshuai@iphy.ac.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant Nos 61425015, 11704006), the Strategic Priority Research Program of Chinese Academy of Sciences (Grant No. XDB28000000), and the National Key Research and Development Program of China (Grant No. 2016YFA0300600)

文章全文 : translate this paragraph

参考文献

[1]	Wolf S A, Awschalom D D, Buhrman R A, Daughton J M, Molna S V, Roukes M L, Chtchelkanova A Y, Treger D M 2001 Science 294 1488 Google Scholar
[2]	Fert A 2008 Rev. Mod. Phys. 80 1517 Google Scholar
[3]	刘兴翀, 路忠林, 任尚坤, 张凤鸣, 都有为, 刘存业, 匡安龙 2005 54 2934 Liu X C, Lu Z L, Ren S K, Zhang F M, Du Y W, Liu C Y, Kuang A L 2005 Acta Phys. Sin. 54 2934
[4]	Coey J M D, Chien C L 2003 MRS Bull. 28 720 Google Scholar
[5]	Johnson P D 1997 Rep. Prog. Phys. 60 1217 Google Scholar
[6]	Meservey R, Tedrow P M 1994 Phys. Rep. 238 173 Google Scholar
[7]	Soulen Jr R J, Byers J M, Osofsky M S, Nadgorny B, Ambrose T, Cheng S F, Broussard P R, Tanaka C T, Nowak J, Moodera J S, Barry A, Coey J M D 1998 Science 282 85 Google Scholar
[8]	Jong M J M, Beenakker C W J 1995 Phys. Rev. Lett. 74 1657 Google Scholar
[9]	Blonder G E, Tinkham M 1983 Phys. Rev. B 27 112
[10]	Blonder G E, Tinkham M, Klapwijk T M 1982 Phys. Rev. B 25 4515 Google Scholar
[11]	Mazin I I 1999 Phys. Rev. Lett. 83 1427 Google Scholar
[12]	吴义华, 王振彦, 沈瑞 2009 58 8591 Wu Y H, Wang Z Y, Shen R 2009 Acta Phys. Sin. 58 8591
[13]	Strijkers G J, Ji Y, Yang F Y, Chien C L, Byers J M 2001 Phys. Rev. B 63 104510 Google Scholar
[14]	Woods G T, Soulen Jr R J, Mazin I I, Nadgorny B, Osofsky M S, Sanders J, Srikanth H 2004 Phys. Rev. B 70 054416 Google Scholar
[15]	Duif A M, Jansen A G M, Wyder P 1989 J. Phys. Condens. Mat. 1 3157 Google Scholar
[16]	Ji Y, Strijkers G J, Yang F Y, Chien C L, Byers J M, Anguelouch A, Xiao G, Gupta A 2001 Phys. Rev. Lett. 86 5585 Google Scholar
[17]	Ren C, Trbovic J, Kallaher R L, Braden J G, Parker J S, von Molnár S, Xiong P 2007 Phys. Rev. B 75 205208 Google Scholar
[18]	Parker J S, Watts S M, Ivanov P G, Xiong P 2002 Phys. Rev. Lett. 88 196601 Google Scholar
[19]	Stokmaier M, Goll G, Weissenberger D, Sürgers C, von Löhneysen H 2008 Phys. Rev. Lett. 101 147005 Google Scholar
[20]	Bugoslavsky Y, Miyoshi Y, Clowes S K, Branford W R, Lake M, Brown I, Caplin A D, Cohen L F 2005 Phys. Rev. B 71 104523 Google Scholar
[21]	Zhang X H, Yu L Q, von Molnár S, Fisk Z, Xiong P 2009 Phys. Rev. Lett. 103 106602 Google Scholar
[22]	Guan T, Lin C, Yang C, Shi Y, Ren C, Li Y, Weng H, Dai X, Fang Z, Yan S, Xiong P 2015 Phys. Rev. Lett. 115 087002 Google Scholar
[23]	Morosan E, Zandbergen H W, Li L, Lee M, Checkelsky J G, Heinrich M, Siegrist T, Ong N P, Cava R J 2007 Phys. Rev. B 75 104401 Google Scholar
[24]	Narita H, Ikuta H, Hinode H, Uchida T, Ohtani T, Wakihara M 1994 J. Solid State Chem. 108 148 Google Scholar
[25]	Gong C, Li L, Li Z, Ji H, Stern A, Xia Y, Cao T, Bao W, Wang C, Wang Y, Qiu Z Q, Cava R J, Louie S G, Xia J, Zhang X 2017 Nature 546 265 Google Scholar
[26]	Novoselov K S, Mishchenko A, Carvalho A, Castro Neto A H 2016 Science 353 aac9439 Google Scholar
[27]	Deng Y, Yu Y, Song Y, Zhang J, Wang N Z, Sun Z, Yi Y, Wu Y Z, Wu S, Zhu J, Wang J, Chen X H, Zhang Y 2018 Nature 563 94 Google Scholar
[28]	Mankovsky S, Chadova K, Ködderitzsch D, Minár J, Ebert H, Bensch W 2015 Phys. Rev. B 92 144413 Google Scholar
[29]	Ko K T, Kim K, Kim S B, Kim H D, Kim J Y, Min B I, Park J H, Chang F H, Lin H J, Tanaka A, Cheong S W 2011 Phys. Rev. Lett. 107 247201 Google Scholar
[30]	Arai M, Moriya R, Yabuki N, Masubuchi S, Ueno K, Machida T 2015 Appl. Phys. Lett. 107 103107 Google Scholar
[31]	Horibe Y, Yang J, Cho Y H, Luo X, Kim S B, Oh Y S, Huang F T, Asada T, Tanimura M, Jeong D, Cheong S W 2014 J. Am. Chem. Soc. 136 8368 Google Scholar
[32]	Checkelsky J G, Lee M, Morosan E, Cava R J, Ong N P 2008 Phys. Rev. B 77 014433 Google Scholar
[33]	Chen C W, Chikara S, Zapf V S, Morosan E 2016 Phys. Rev. B 94 054406 Google Scholar
[34]	Hardy W J, Chen C W, Marcinkova A, Ji H, Sinova J, Natelson D, Morosan E 2015 Phys. Rev. B 91 054426 Google Scholar
[35]	Reefman D, Baak J, Brom H B, Wiegers G A 1990 Solid State Commun. 75 47 Google Scholar
[36]	Zhang X, von Molnár S, Fisk Z, Xiong P 2008 Phys. Rev. Lett. 100 167001 Google Scholar
[37]	Nowack A, Heinz A, Oster F, Wohlleben D, Güntherodt G, Fisk Z, Menovsky A 1987 Phys. Rev. B 36 2436(R)Google Scholar
[38]	Rodrigo J G, Guinea F, Vieira S, Aliev F G 1997 Phys. Rev. B 55 14318 Google Scholar

施引文献

图 1 Fe_0.26TaS₂单晶样品的磁性测量结果　(a) 外加磁场垂直于ab面(H⊥ab)时的FC和ZFC磁化曲线, 测量磁场为100 Oe (1 Oe = 10³/(4π) A/m); (b)外加磁场平行于ab面时 (H//ab)的FC和ZFC磁化曲线, 测量磁场为100 Oe; (c) H⊥ab的等温磁化曲线随外加磁场的变化; (d) H//ab的等温磁化曲线随外加磁场的变化(为清楚起见, 在垂直方向做了等间距平移)

Fig. 1. Magnetization measurement results of Fe_0.26TaS₂: (a) Magnetization measurement with ZFC and FC process while H⊥ab, the measurement field is 100 Oe; (b) magnetization measurement with ZFC and FC process while H//ab, the measurement field is 100 Oe; (c) isothermal magnetization measurements for H⊥ab; (d) isothermal magnetization measurements for H//ab. For clarify, the data is shift equally in Fig. 1(d).

下载: 全尺寸图片幻灯片

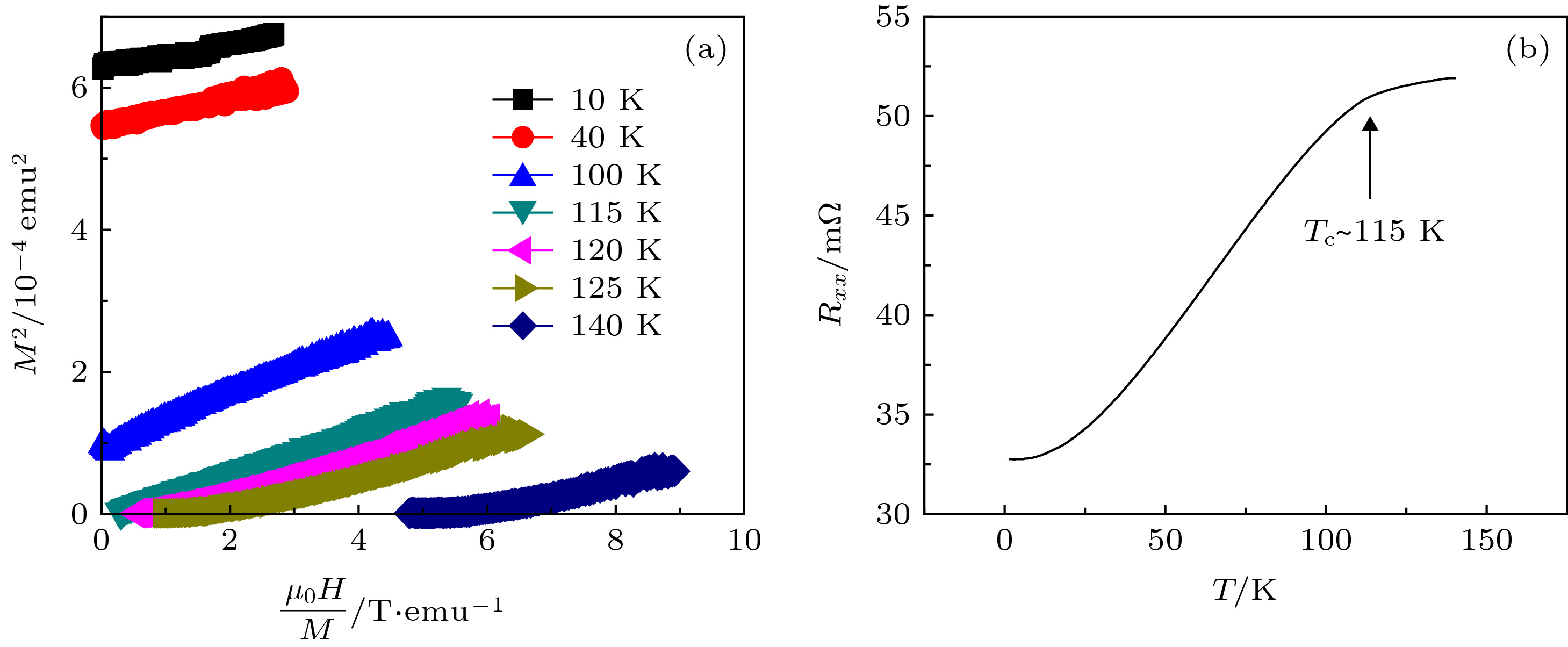
图 2 Fe_0.26TaS₂等温磁化曲线和电阻-温度曲线(1 emu = 10^–3 A·m²)　(a) H⊥ab方向Fe_0.26TaS₂等温磁化曲线的Arrott图, 居里温度为115 K; (b) Fe_0.26TaS₂的电阻-温度曲线

Fig. 2. Isothermal magnetization and temperature dependence of resistance of Fe_0.26TaS₂: (a) Arrot plot for isothermal magnetization in H⊥ab; (b) temperature dependence of resistance.

下载: 全尺寸图片幻灯片

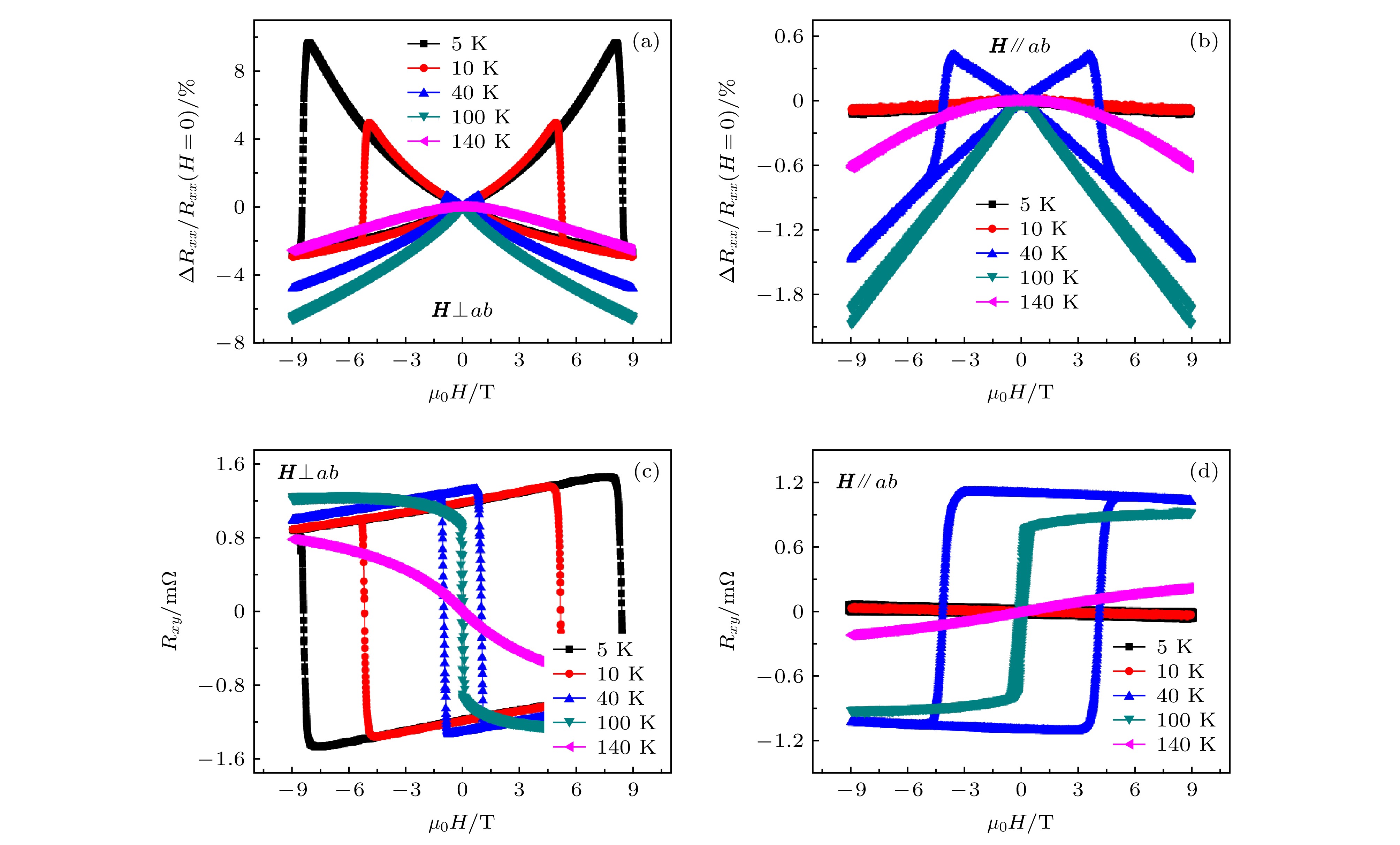
图 3 磁电阻和霍尔电阻随外加磁场的变化　(a) H⊥ab时, 磁电阻随外加磁场的变化; (b) H//ab时, 磁电阻随外加磁场的变化; (c) H⊥ab时, 霍尔电阻随外加磁场的变化; (d) H//ab时, 霍尔电阻随外加磁场的变化

Fig. 3. Magnetic field dependence of magnetoresistance and Hall effect: (a) Magnetic field dependence of magnetoresistance, H⊥ab; (b) magnetic field dependence of magnetoresistance, H//ab; (c) magnetic field dependence of Hall effect, H⊥ab; (d) magnetic field dependence of Hall effect, H//ab.

下载: 全尺寸图片幻灯片

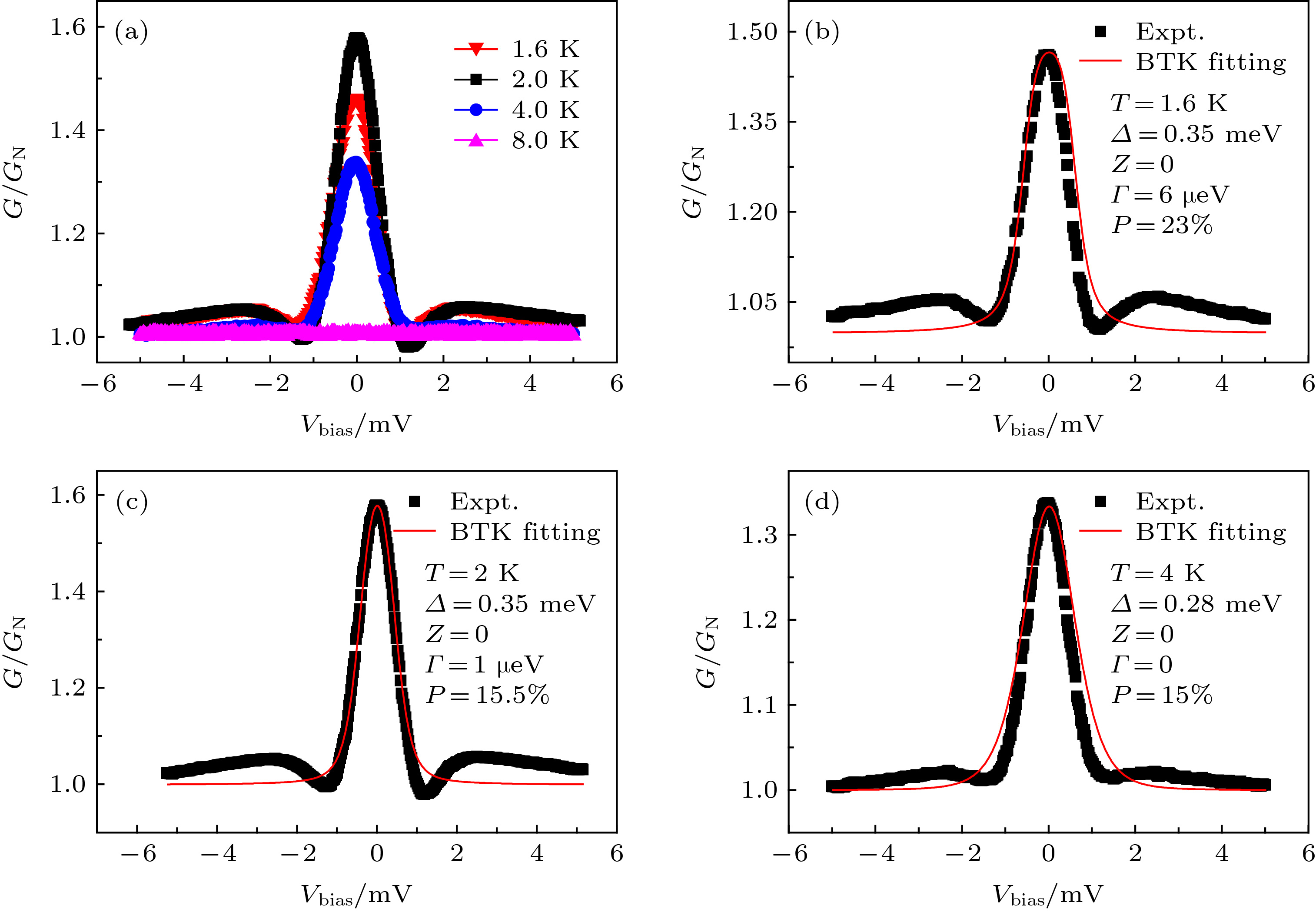
图 4 Fe_0.26TaS₂/Pb的Andreev反射谱　(a)不同温度下Andreev结的归一化微分电导谱; (b) T = 1.6 K, 修正的BTK理论对微分电导谱的拟合结果; (c) T = 2 K, 修正的BTK理论对微分电导谱的拟合结果; (d) T = 4 K, 修正的BTK理论对微分电导谱的拟合结果. 黑色点为实验数据, 红色线为理论计算结果

Fig. 4. Andreev reflection spectroscopy of Fe_0.26TaS₂/Pb: (a) Normalization of Andreev reflection spectroscopy from T = 2 K to 8 K; (b) modified BTK fitting for normalized Andreev reflection spectroscopy, T = 1.6 K; (c) modified BTK fitting for normalized Andreev reflection spectroscopy, T = 2 K; (d) modified BTK fitting for normalized Andreev reflection spectroscopy, T = 4 K. The black dot is experimental data and red line is fitting.

下载: 全尺寸图片幻灯片

图 5 Fe_0.26TaS₂/Al/Pb异质结的Andreev反射谱　(a)不同温度下的归一化微分电导谱; (b) T = 0.36 K, 修正的BTK理论对微分电导谱的拟合结果; (c) T = 1 K, 修正的BTK理论对微分电导谱的拟合结果; (d) T = 6 K, 修正的BTK理论对微分电导谱的拟合结果; 黑色点为实验数据, 红色线为理论计算结果, 自旋极化率P ≠ 0

Fig. 5. Andreev reflection spectroscopy of Fe_0.26TaS₂/Al/Pb: (a) Normalization of Andreev reflection reflection spectroscopy from T = 0.36 K to 9 K; (b) modified BTK fitting for normalized Andreev reflection spectroscopy, T = 0.36 K; (c) modified BTK fitting for normalized Andreev reflection spectroscopy, T = 1 K; (d) modified BTK fitting for normalized Andreev reflection spectroscopy, T = 6 K. The black dot is experimental data and red line is fitting. Spin polarization is fixed to none-zero (P ≠ 0).

下载: 全尺寸图片幻灯片

图 6 修正的BTK理论对不同温度下微分电导谱的拟合结果　(a) T = 0.36 K; (b) T = 1 K; (c) T = 3 K; (d) T = 6 K; 黑色点为实验数据, 红色线为理论计算结果; 自旋极化率固定为零(P = 0)

Fig. 6. Modified BTK fitting for normalized Andreev reflection spectroscopy of Fe_0.26TaS₂/Al/Pb: (a) T = 0.36 K; (b) T = 1 K; (c) T = 3 K; (d) T = 6 K. The black dot is experimental data and the red line is fitting. Spin polarization is fixed to zero (P = 0).

下载: 全尺寸图片幻灯片

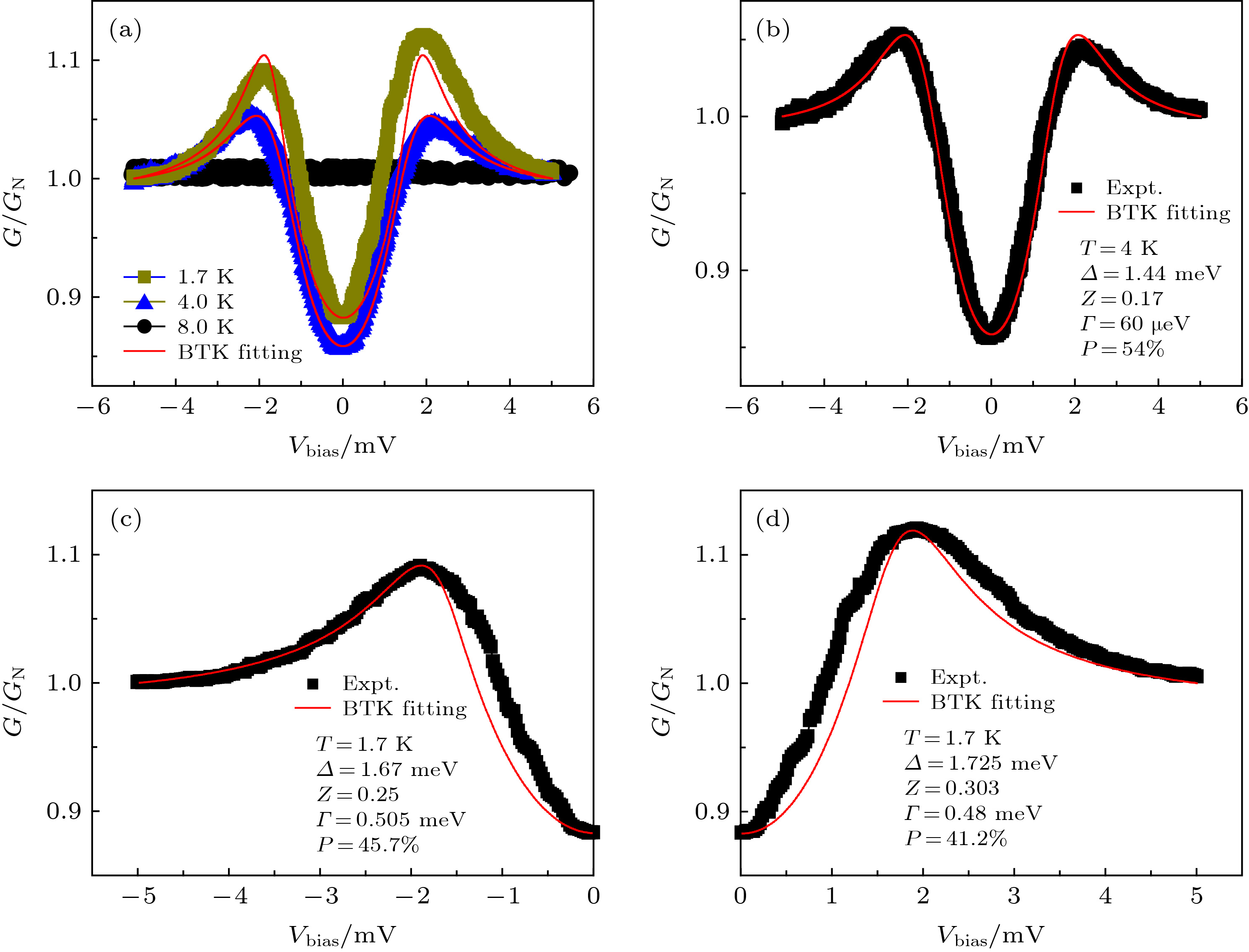
图 7 Fe_0.26TaS₂/NbSe₂的Andreev反射谱　(a)不同温度下的归一化微分电导谱和修正的BTK拟合; (b) T = 4 K的微分电导谱和修正的BTK拟合; (c) T = 1.7 K下, 负偏压的归一化微分电导谱及修正的BTK拟合; (d) T = 1.7 K下, 正偏压的归一化微分电导谱及修正的BTK拟合; 黑色点为实验数据, 红色线为理论计算结果

Fig. 7. Andreev reflection spectroscopy of Fe_0.26TaS₂//NbSe₂: (a) Normalization of Andreev reflection spectroscopy from T = 1.7 K to 8 K; (b) modified BTK fitting for normalized Andreev reflection spectroscopy at T = 4 K; (c) modified BTK fitting for normalized Andreev reflection spectroscopy at T = 1.7 K; (d) modified BTK fitting respectively for negative bias or positive bias Andreev reflection spectroscopy at T = 1.7 K. The black dot is experimental data and red line is fitting.

下载: 全尺寸图片幻灯片

map

[1]	Wolf S A, Awschalom D D, Buhrman R A, Daughton J M, Molna S V, Roukes M L, Chtchelkanova A Y, Treger D M 2001 Science 294 1488 Google Scholar
[2]	Fert A 2008 Rev. Mod. Phys. 80 1517 Google Scholar
[3]	刘兴翀, 路忠林, 任尚坤, 张凤鸣, 都有为, 刘存业, 匡安龙 2005 54 2934 Liu X C, Lu Z L, Ren S K, Zhang F M, Du Y W, Liu C Y, Kuang A L 2005 Acta Phys. Sin. 54 2934
[4]	Coey J M D, Chien C L 2003 MRS Bull. 28 720 Google Scholar
[5]	Johnson P D 1997 Rep. Prog. Phys. 60 1217 Google Scholar
[6]	Meservey R, Tedrow P M 1994 Phys. Rep. 238 173 Google Scholar
[7]	Soulen Jr R J, Byers J M, Osofsky M S, Nadgorny B, Ambrose T, Cheng S F, Broussard P R, Tanaka C T, Nowak J, Moodera J S, Barry A, Coey J M D 1998 Science 282 85 Google Scholar
[8]	Jong M J M, Beenakker C W J 1995 Phys. Rev. Lett. 74 1657 Google Scholar
[9]	Blonder G E, Tinkham M 1983 Phys. Rev. B 27 112
[10]	Blonder G E, Tinkham M, Klapwijk T M 1982 Phys. Rev. B 25 4515 Google Scholar
[11]	Mazin I I 1999 Phys. Rev. Lett. 83 1427 Google Scholar
[12]	吴义华, 王振彦, 沈瑞 2009 58 8591 Wu Y H, Wang Z Y, Shen R 2009 Acta Phys. Sin. 58 8591
[13]	Strijkers G J, Ji Y, Yang F Y, Chien C L, Byers J M 2001 Phys. Rev. B 63 104510 Google Scholar
[14]	Woods G T, Soulen Jr R J, Mazin I I, Nadgorny B, Osofsky M S, Sanders J, Srikanth H 2004 Phys. Rev. B 70 054416 Google Scholar
[15]	Duif A M, Jansen A G M, Wyder P 1989 J. Phys. Condens. Mat. 1 3157 Google Scholar
[16]	Ji Y, Strijkers G J, Yang F Y, Chien C L, Byers J M, Anguelouch A, Xiao G, Gupta A 2001 Phys. Rev. Lett. 86 5585 Google Scholar
[17]	Ren C, Trbovic J, Kallaher R L, Braden J G, Parker J S, von Molnár S, Xiong P 2007 Phys. Rev. B 75 205208 Google Scholar
[18]	Parker J S, Watts S M, Ivanov P G, Xiong P 2002 Phys. Rev. Lett. 88 196601 Google Scholar
[19]	Stokmaier M, Goll G, Weissenberger D, Sürgers C, von Löhneysen H 2008 Phys. Rev. Lett. 101 147005 Google Scholar
[20]	Bugoslavsky Y, Miyoshi Y, Clowes S K, Branford W R, Lake M, Brown I, Caplin A D, Cohen L F 2005 Phys. Rev. B 71 104523 Google Scholar
[21]	Zhang X H, Yu L Q, von Molnár S, Fisk Z, Xiong P 2009 Phys. Rev. Lett. 103 106602 Google Scholar
[22]	Guan T, Lin C, Yang C, Shi Y, Ren C, Li Y, Weng H, Dai X, Fang Z, Yan S, Xiong P 2015 Phys. Rev. Lett. 115 087002 Google Scholar
[23]	Morosan E, Zandbergen H W, Li L, Lee M, Checkelsky J G, Heinrich M, Siegrist T, Ong N P, Cava R J 2007 Phys. Rev. B 75 104401 Google Scholar
[24]	Narita H, Ikuta H, Hinode H, Uchida T, Ohtani T, Wakihara M 1994 J. Solid State Chem. 108 148 Google Scholar
[25]	Gong C, Li L, Li Z, Ji H, Stern A, Xia Y, Cao T, Bao W, Wang C, Wang Y, Qiu Z Q, Cava R J, Louie S G, Xia J, Zhang X 2017 Nature 546 265 Google Scholar
[26]	Novoselov K S, Mishchenko A, Carvalho A, Castro Neto A H 2016 Science 353 aac9439 Google Scholar
[27]	Deng Y, Yu Y, Song Y, Zhang J, Wang N Z, Sun Z, Yi Y, Wu Y Z, Wu S, Zhu J, Wang J, Chen X H, Zhang Y 2018 Nature 563 94 Google Scholar
[28]	Mankovsky S, Chadova K, Ködderitzsch D, Minár J, Ebert H, Bensch W 2015 Phys. Rev. B 92 144413 Google Scholar
[29]	Ko K T, Kim K, Kim S B, Kim H D, Kim J Y, Min B I, Park J H, Chang F H, Lin H J, Tanaka A, Cheong S W 2011 Phys. Rev. Lett. 107 247201 Google Scholar
[30]	Arai M, Moriya R, Yabuki N, Masubuchi S, Ueno K, Machida T 2015 Appl. Phys. Lett. 107 103107 Google Scholar
[31]	Horibe Y, Yang J, Cho Y H, Luo X, Kim S B, Oh Y S, Huang F T, Asada T, Tanimura M, Jeong D, Cheong S W 2014 J. Am. Chem. Soc. 136 8368 Google Scholar
[32]	Checkelsky J G, Lee M, Morosan E, Cava R J, Ong N P 2008 Phys. Rev. B 77 014433 Google Scholar
[33]	Chen C W, Chikara S, Zapf V S, Morosan E 2016 Phys. Rev. B 94 054406 Google Scholar
[34]	Hardy W J, Chen C W, Marcinkova A, Ji H, Sinova J, Natelson D, Morosan E 2015 Phys. Rev. B 91 054426 Google Scholar
[35]	Reefman D, Baak J, Brom H B, Wiegers G A 1990 Solid State Commun. 75 47 Google Scholar
[36]	Zhang X, von Molnár S, Fisk Z, Xiong P 2008 Phys. Rev. Lett. 100 167001 Google Scholar
[37]	Nowack A, Heinz A, Oster F, Wohlleben D, Güntherodt G, Fisk Z, Menovsky A 1987 Phys. Rev. B 36 2436(R)Google Scholar
[38]	Rodrigo J G, Guinea F, Vieira S, Aliev F G 1997 Phys. Rev. B 55 14318 Google Scholar

[1]	王少霞, 赵旭才, 潘多桥, 庞国旺, 刘晨曦, 史蕾倩, 刘桂安, 雷博程, 黄以能, 张丽丽. 过渡金属(Cr, Mn, Fe, Co)掺杂对TiO₂磁性影响的第一性原理研究. , 2020, 69(19): 197101. doi: 10.7498/aps.69.20200644
[2]	王宗, 侯兴元, 潘伯津, 谷亚东, 张孟迪, 张凡, 陈根富, 任治安, 单磊. Re₃W的点接触安德烈夫反射谱研究. , 2019, 68(1): 017402. doi: 10.7498/aps.68.20181996
[3]	杨芝, 张悦, 周倩倩, 王玉华. Fe3O4单晶薄膜磁性电场调控的微磁学仿真研究. , 2017, 66(13): 137501. doi: 10.7498/aps.66.137501
[4]	刘红艳, 柳祝红, 李歌天, 马星桥. Ga含量对Mn2-xNiGa1+x结构和磁性的影响. , 2016, 65(4): 048102. doi: 10.7498/aps.65.048102
[5]	姜恩海, 朱兴凤, 陈凌孚. Heusler合金Co2MnAl(100)表面电子结构、磁性和自旋极化的第一性原理研究. , 2015, 64(14): 147301. doi: 10.7498/aps.64.147301
[6]	姜丽娜, 张玉滨, 董顺乐. 有机自旋器件磁性渗透层中双极化子对自旋极化输运的影响. , 2015, 64(14): 147104. doi: 10.7498/aps.64.147104
[7]	杨育奇, 高庆庆, 李冠男. 组合结构化合物Ho2Ni7-xFex (x=03.0)的晶体结构、结构转变和磁性. , 2013, 62(1): 016103. doi: 10.7498/aps.62.016103
[8]	王瑞琴, 宫箭, 武建英, 陈军. 对称双势垒量子阱中自旋极化输运的时间特性. , 2013, 62(8): 087303. doi: 10.7498/aps.62.087303
[9]	杜音, 王文洪, 张小明, 刘恩克, 吴光恒. 铁基Heusler合金Fe2Co1-xCrxSi的结构、磁性和输运性质的研究. , 2012, 61(14): 147304. doi: 10.7498/aps.61.147304
[10]	赵昆, 张坤, 王家佳, 于金, 吴三械. Heusler合金Pd2 CrAl四方变形、磁性及弹性常数的第一性原理计算. , 2011, 60(12): 127101. doi: 10.7498/aps.60.127101
[11]	罗礼进, 仲崇贵, 方靖淮, 赵永林, 周朋霞, 江学范. Heusler合金Mn2 NiAl的电子结构和磁性对四方畸变的响应及其压力响应. , 2011, 60(12): 127502. doi: 10.7498/aps.60.127502
[12]	高潭华, 卢道明, 吴顺情, 朱梓忠. Fe原子薄片的磁性:第一性原理计算. , 2011, 60(4): 047502. doi: 10.7498/aps.60.047502
[13]	何志刚, 程兴华, 龚敏, 蔡娟露, 石瑞英. 影响磁性pn结自旋极化输运特性的因素. , 2010, 59(9): 6521-6526. doi: 10.7498/aps.59.6521
[14]	韩立安, 陈长乐, 董慧迎, 王建元, 高国棉, 罗炳成. 层状钙钛矿La1.3Sr1.7Mn2-xCuxO7的磁性及电特性. , 2008, 57(1): 541-544. doi: 10.7498/aps.57.541
[15]	韩薇, 常树全, 戴耀东, 陈达, 黄彦君. 氰根桥联Ni(Ⅱ)-Fe(Ⅲ)类纳米分子磁体磁性及穆斯堡尔谱研究. , 2008, 57(4): 2493-2499. doi: 10.7498/aps.57.2493
[16]	刘锦宏, 张凌飞, 田庚方, 李济晨, 李发伸. 低温固相反应法制备的NiFe2O4纳米颗粒的结构与磁性. , 2007, 56(10): 6050-6055. doi: 10.7498/aps.56.6050
[17]	庞利佳, 孙光飞, 陈菊芳, 强文江, 张锦标, 黎文安. 纳米晶复合Pr2Fe14B/α-Fe永磁材料磁性的研究. , 2006, 55(6): 3049-3053. doi: 10.7498/aps.55.3049
[18]	张炜, 千正男, 隋郁, 刘玉强, 苏文辉, 张铭, 柳祝红, 刘国栋, 吴光恒. Heusler合金Co2TiSn的磁性与输运性能. , 2005, 54(10): 4879-4883. doi: 10.7498/aps.54.4879
[19]	王本阳, 千正男, 隋郁, 刘玉强, 苏文辉, 张铭, 柳祝红, 刘国栋, 吴光恒. Heusler合金Cu2VAl磁性及输运性质的研究. , 2005, 54(7): 3386-3390. doi: 10.7498/aps.54.3386
[20]	郭鸿涌, 刘宝丹, 唐宁, 罗鸿志, 李养贤, 杨伏明, 吴光恒. Co和稳定元素对Nd3(Fe,Co,M)29(M=Ti,V,Cr) 化合物结构和磁性的影响. , 2004, 53(1): 189-193. doi: 10.7498/aps.53.189

计量

文章访问数: 10274
PDF下载量: 236
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

层状铁磁体Fe_0.26TaS₂的Andreev反射谱