拓扑表面等离激元

耿逸飞; 王铸宁; 马耀光; 高飞

doi:10.7498/aps.68.20191085

摘要

集成电磁器件尺寸的小型化一直都是该领域发展的重要方向, 具有亚波长、强束缚模式特性的表面等离激元电磁模式为集成电磁器件小型化提供了有力的解决方案. 但是, 支持表面等离激元的材料或结构不可避免地会出现杂质或者结构缺陷, 从而降低表面电磁波器件的传输性能. 为了避免表面等离激元器件性能受到杂质或缺陷的影响, 具有鲁棒传输特性的拓扑表面等离激元应运而生. 本文首先回顾了光频段表面等离激元和太赫兹/微波频段人工表面等离激元的实现方案以及电磁特性, 进而重点总结了拓扑表面等离激元的几种重要设计理论, 并展望了拓扑表面等离激元的未来发展方向.

关键词:

Abstract

The miniaturization of electromagnetic devices is a long-term theme for the development of modern technologies to achieve higher flexibilities, better performances, and higher density integration. Surface plasmon polaritons (SPPs) provide a powerful solution for reducing the size of integrated electromagnetic device due to its deep subwavelength confinement. However, materials or structures that support SPPs inevitably have impurities or structural defects, which leads to the loss of the propagating mode. In order to avoid scattering from impurities or defects, topological structures are introduced to address issues of discontinuities and have been proved to be an effective solution. In this paper, we first review the recent efforts devoted to SPPs based optical devices and those of artificial surface plasmon in terahertz/microwave band, and then summarize several important topological systems of SPPs. Finally, we present our perspectives on the future developments of this field.

Keywords:

作者及机构信息

1.
浙江大学, 现代光学仪器国家重点实验室, 杭州　310027

2.
浙江大学信息与电子工程学院, 杭州　310027

通信作者: 马耀光, mayaoguang@zju.edu.cn ; 高飞, gaofeizju@zju.edu.cn

基金项目: 国家自然科学基金青年科学基金(批准号: 61801426)资助的课题

Authors and contacts

1.
State Key Laboratory of Modern Optical Instruments, Zhejiang University, Hangzhou 310027, China

2.
College of Information Science & Electronic Engineering, Zhejiang University, Hangzhou 310027, China

Corresponding author: Ma Yao-Guang, mayaoguang@zju.edu.cn ; Gao Fei, gaofeizju@zju.edu.cn

Funds: Project supported by the Young Scientists Fund of the National Natural Science Foundation of China (Grant No. 61801426)

文章全文 : translate this paragraph

参考文献

[1]	Wood R W 1902 The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science (Abingdon: Taylor & Francis) pp4–396
[2]	Pines D 1956 Rev. Mod. Phys. 28 184 Google Scholar
[3]	Ritchie R H 1957 Phys. Rev. 106 874 Google Scholar
[4]	Ritchie R H, Arakawa E, Cowan J, Hamm R 1968 Phys. Rev. Lett. 21 1530 Google Scholar
[5]	Cunningham S, Maradudin A, Wallis R 1974 Phys. Rev. B 10 3342 Google Scholar
[6]	Pendry J B, Martin-Moreno L, Garcia-Vidal F J 2004 Science 305 847 Google Scholar
[7]	Garcia-Vidal F J, Martin-Moreno L, Pendry J B 2005 J. Opt. A: Pure Appl. Opt 7 S97 Google Scholar
[8]	Qi X L, Zhang S C 2011 Rev. Mod. Phys. 83 54
[9]	Hasan M Z, Kane C L 2010 Rev. Mod. Phys. 82 3045 Google Scholar
[10]	Haldane F D M, Raghu S 2008 Phys. Rev. Lett. 100 013904 Google Scholar
[11]	Wang Z, Chong Y D, Joannopoulos J D, Soljacic M 2009 Nature 461 772 Google Scholar
[12]	Lu L, Joannopoulos J D, Soljačić M 2014 Nat. Photonics 8 821 Google Scholar
[13]	Chen W J, Jiang S J, Chen X D, Zhu B C, Zhou L, Dong J W, Chan C T 2014 Nat. Commun. 5 5782 Google Scholar
[14]	Gao F, Gao Z, Shi X H, Yang Z J, Lin X, Xu H Y, Joannopoulos J D, Soljacic M, Chen H S, Lu L, Chong Y D, Zhang B L 2016 Nat. Commun. 7 11619 Google Scholar
[15]	Cheng X J, Jouvaud C, Ni X, Mousavi S H, Genack A Z, Khanikaev A B 2016 Nat. Mater. 15 542 Google Scholar
[16]	Dong J W, Chen X D, Zhu H Y, Wang Y, Zhang X 2017 Nat. Mater. 16 298 Google Scholar
[17]	Gao F, Xue H R, Yang Z J, Lai K F, Yu Y, Lin X, Chong Y D, Shvets G, Zhang B L 2018 Nat. Phys. 14 140 Google Scholar
[18]	Gao W L, Lawrence M, Yang B A, Liu F, Fang F Z, Beri B, Li J S, Zhang S 2015 Phys. Rev. Lett. 114 037402 Google Scholar
[19]	Hafezi M, Mittal S, Fan J, Migdall A, Taylor J M 2013 Nat. Photonics 7 1001 Google Scholar
[20]	Khanikaev A B, Mousavi S H, Tse W K, Kargarian M, MacDonald A H, Shvets G 2013 Nat. Mater. 12 233 Google Scholar
[21]	Liang G, Chong Y 2013 Phys. Rev. Lett. 110 203904 Google Scholar
[22]	Ma T, Khanikaev A B, Mousavi S H, Shvets G 2015 Phys. Rev. Lett. 114 127401 Google Scholar
[23]	Ma T, Shvets G 2016 New J. Phys. 18 025012 Google Scholar
[24]	Noh J, Huang S, Chen K P, Rechtsman M C 2018 Phys. Rev. Lett. 120 063902 Google Scholar
[25]	Pasek M, Chong Y D 2014 Phys. Rev. B 89 075113 Google Scholar
[26]	Rechtsman M C, Zeuner J M, Plotnik Y, Lumer Y, Podolsky D, Dreisow F, Nolte S, Segev M, Szameit A 2013 Nature 496 196 Google Scholar
[27]	Wu L H, Hu X 2015 Phys. Rev. Lett. 114 223901 Google Scholar
[28]	Xiao M, Lin Q, Fan S H 2016 Phys. Rev. Lett. 117 057401 Google Scholar
[29]	Lu L, Joannopoulos J D, Soljacic M 2016 Nat. Phys. 12 626 Google Scholar
[30]	Jin D, Christensen T, Soljačić M, Fang N X, Lu L, Zhang X 2017 Phys. Rev. Lett. 118 245301 Google Scholar
[31]	Pan D, Yu R, Xu H, de Abajo F J G 2017 Nat. Commun. 8 1243 Google Scholar
[32]	Jung M, Fan Z, Shvets G 2018 Phys. Rev. Lett. 121 086807 Google Scholar
[33]	Gao Z, Gao F, Zhang Y M, Xu H Y, Luo Y, Zhang B L 2017 Adv. Mater. 29 1700018 Google Scholar
[34]	Murakami S, Nagaosa N, Zhang S C 2003 Science 301 1348 Google Scholar
[35]	Kane C L, Mele E J 2005 Phys. Rev. Lett. 95 226801 Google Scholar
[36]	Haldane F D M 1988 Phys. Rev. Lett. 61 2015 Google Scholar
[37]	Yves S, Fleury R, Berthelot T, Fink M, Lemoult F, Lerosey G 2017 Nat. Commun. 8 16023 Google Scholar
[38]	Xu X D, Yao W, Xiao D, Heinz T F 2014 Nat. Phys. 10 343 Google Scholar
[39]	Mak K F, McGill K L, Park J, McEuen P L 2014 Science 344 1489 Google Scholar
[40]	Ju L, Shi Z W, Nair N, Lv Y C, Jin C H, Velasco J, Ojeda-Aristizabal C, Bechtel H A, Martin M C, Zettl A, Analytis J, Wang F 2015 Nature 520 650 Google Scholar
[41]	Gao Z, Yang Z J, Gao F, Xue H R, Yang Y H, Dong J W, Zhang B L 2017 Phys. Rev. B 96 201402 Google Scholar
[42]	Wu X X, Meng Y, Tian J X, Huang Y Z, Xiang H, Han D Z, Wen W J 2017 Nat. Commun. 8 1304 Google Scholar
[43]	Yin X B, Ye Z L, Rho J, Wang Y, Zhang X 2013 Science 339 1405 Google Scholar
[44]	Kitagawa T, Berg E, Rudner M, Demler E 2010 Phys. Rev. B 82 235114 Google Scholar
[45]	Kitagawa T, Rudner M S, Berg E, Demler E 2010 Phys. Rev. A 82 033429 Google Scholar
[46]	Rudner M S, Lindner N H, Berg E, Levin M 2013 Phys. Rev. X 3 031005
[47]	Lohse M, Schweizer C, Price H M, Zilberberg O, Bloch I 2018 Nature 553 55 Google Scholar
[48]	Zilberberg O, Huang S, Guglielmon J, Wang M H, Chen K P, Kraus Y E, Rechtsman M C 2018 Nature 553 59 Google Scholar
[49]	Benalcazar W A, Bernevig B A, Hughes T L 2017 Science 357 61 Google Scholar
[50]	Khanikaev A B, Mousavi S H, Shvets G, Kivshar Y S 2010 Phys. Rev. Lett. 105 126804 Google Scholar
[51]	Leykam D, Chong Y D 2016 Phys. Rev. Lett. 117 143901 Google Scholar
[52]	Ni X, Purtseladze D, Smirnova D A, Slobozhanyuk A, Alù A, Khanikaev A B 2018 Sci. Adv. 4 eaap8802 Google Scholar
[53]	Yu N F, Wang Q J, Kats M A, Fan J A, Khanna S P, Li L H, Davies A G, Linfield E H, Capasso F 2010 Nat. Mater. 9 730 Google Scholar
[54]	Karl N J, McKinney R W, Monnai Y, Mendis R, Mittleman D M 2015 Nat. Photonics 9 717 Google Scholar
[55]	Ma J J, Karl N J, Bretin S, Ducournau G, Mittleman D M 2017 Nat. Commun. 8 729 Google Scholar
[56]	Grady N K, Heyes J E, Chowdhury D R, Zeng Y, Reiten M T, Azad A K, Taylor A J, Dalvit D A, Chen H T 2013 Science 340 1304 Google Scholar
[57]	Chen H T, O'hara J F, Azad A K, Taylor A J, Averitt R D, Shrekenhamer D B, Padilla W J 2008 Nat. Photonics 2 295 Google Scholar

施引文献

图 1 (a)杂质和结构缺陷对表面等离激元传输的影响; (b)拓扑表面等离激元的鲁棒传输特性

Fig. 1. (a) Effect of impurity and structural defects on surface plasmon transport; (b) robust propagation characteristics of topological surface plasmons.

下载: 全尺寸图片幻灯片

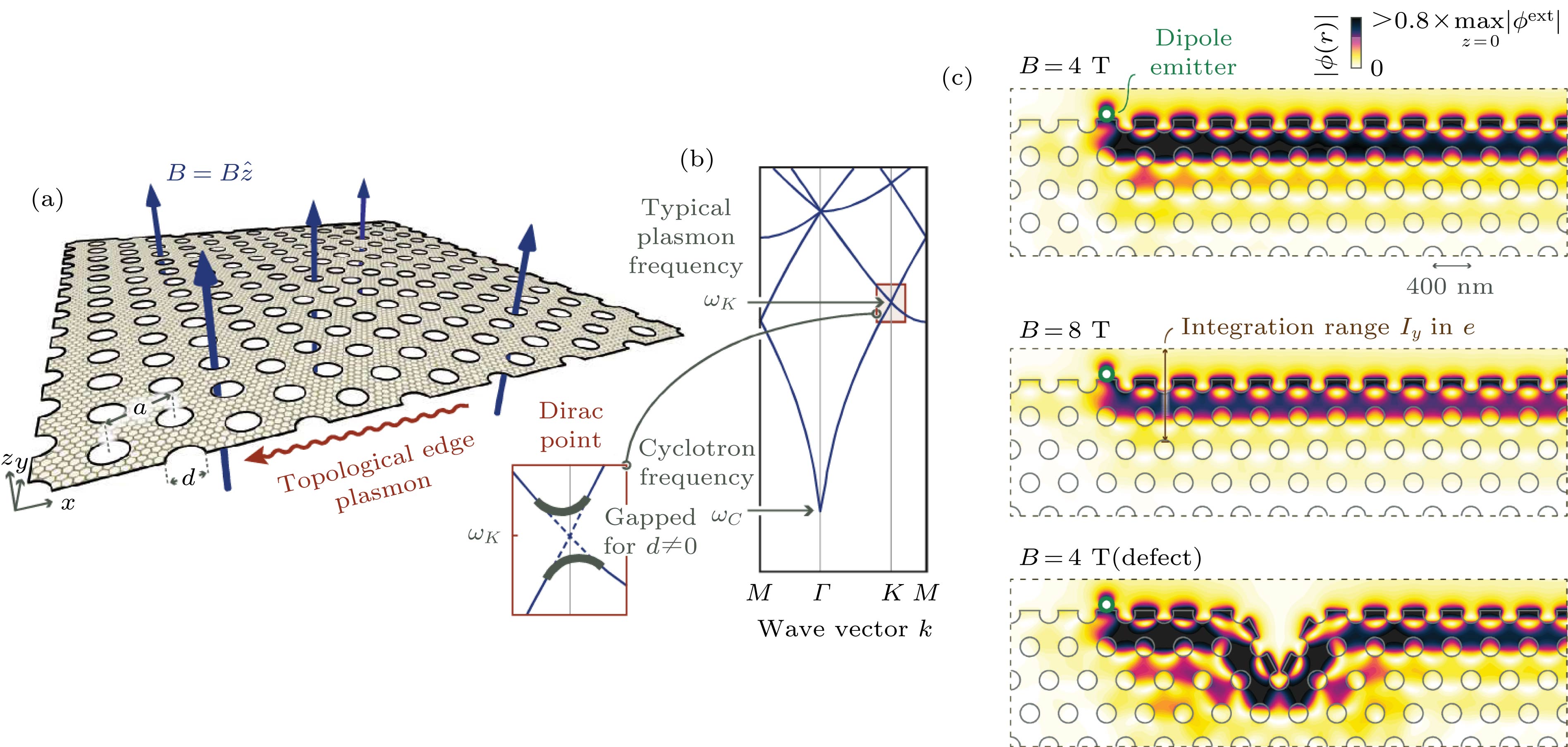
图 2 二维拓扑表面等离激元晶体及其边界态^[30]　(a)石墨烯中圆孔三角点阵的示意图, 在外加磁场B作用下, 有限晶格支持拓扑保护的单向边缘等离子体; (b)在B ≠ 0的石墨烯中的等离激元色散能带, 当孔径d ≠ 0, 出现完全带隙; (c)不同磁感应强度下的边界态及其鲁棒性

Fig. 2. Two-dimensional topological surface plasmon crystals and their boundary states ^[30]: (a) Schematic diagram of triangular circular hole lattices in graphene, under the action of an applied magnetic field B, finite lattices support a unidirectional edge plasma with topological protection; (b) energy band diagram of plasmon in graphene of B ≠ 0, when d ≠ 0, the complete band gap appears; (c) edge states under different magnetic induction and their robustness

下载: 全尺寸图片幻灯片

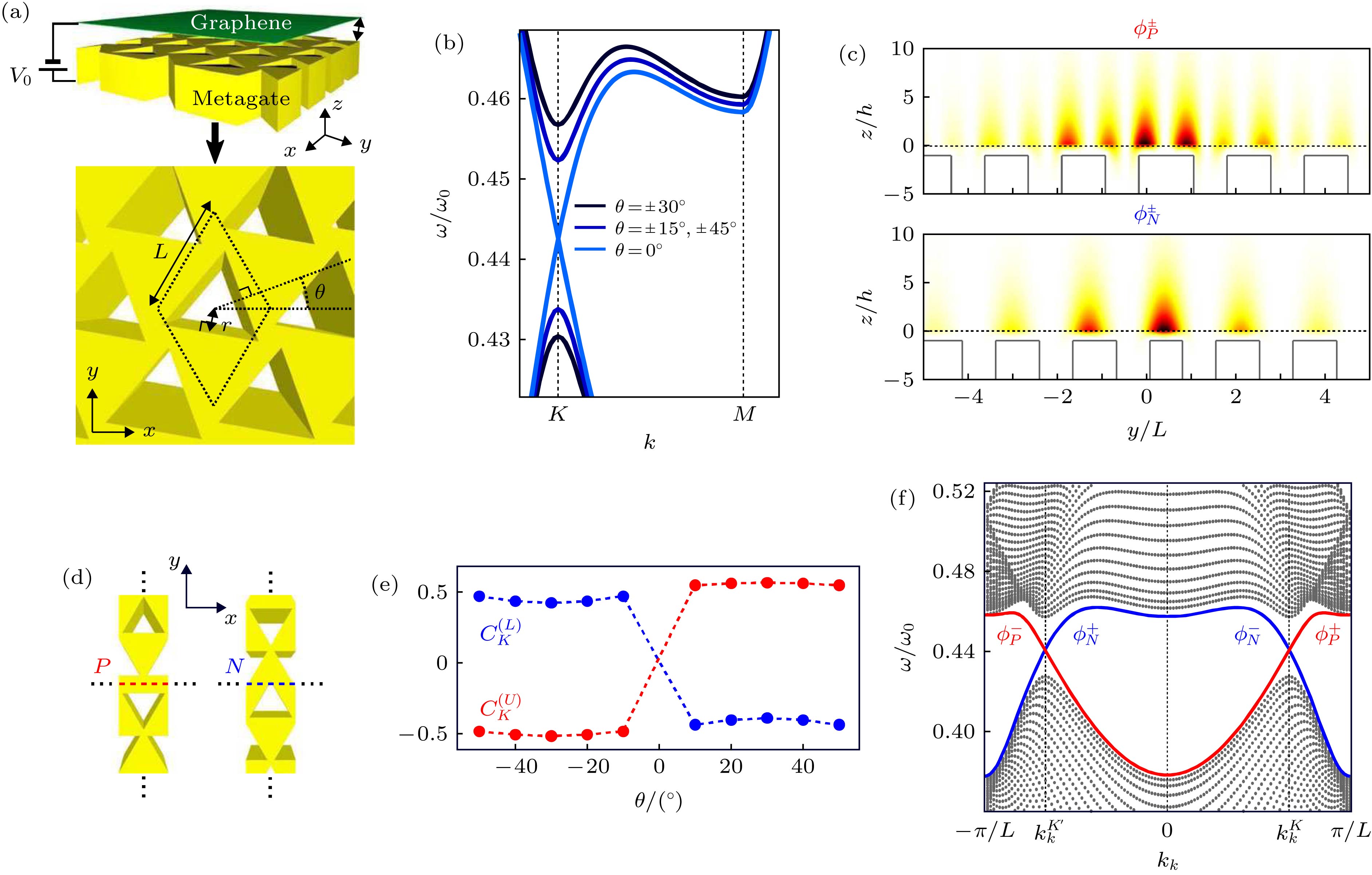
图 3 (a)基于石墨烯的能谷等离子激元晶体示意图: 由偏置电压V₀与相对于石墨烯晶格存在夹角的栅结构; (b)狄拉克点处的能带; (c) yz(x = 0)平面上的电场分布; (d)两种类型的边界; (e)不同夹角对应的谷陈数值; (f)图(d)所示一维结构能带^[32]

Fig. 3. (a) Schematic diagram of graphene-based energy valley plasmon crystals: a gate structure with a biased voltage V₀ and an angle with respect to the graphene lattice; (b) energy band at the Dirac point; (c) electric field distribution on the yz (x = 0) plane; (d) two types of boundaries; (e) valley chern numbers corresponding to different angles; and (f) the one-dimensional structural energy band shown in Fig. (d).

下载: 全尺寸图片幻灯片

图 4 人工表面等离激元QSH^[27,37]　(a)基于介质圆柱的光子QSH阵列; (b)图(a)中结构的能带; (c)单元胞收缩的SSPPs结构; (d)单元胞扩张的SSPPs结构; (e)SSPPs结构的能带仿真结果; (f)通过组合(c)和(d)中的结构构建边界; (g)边界态的模场分布

Fig. 4. Spoof plasmonic QSH^[27,37]: (a) Photonic QSH with dielectric cylinders, the zoom in figure shows the hexagonal cluster; (b) edge states of photonic QSH; (c) spoof plasmonic structure whose unit cells of hexagonal clusters get shrunk, leading to zero spin Chern number; (d) spoof plasmonic structure whose unit cells of hexagonal clusters get expanded, which generates non vanishing spin Chern number; (e) simulated edge states at a domain wall between structures of (c) and (d); (f) constructed domain wall by combining structures in (c) and (d); (g) field patterns of edge states

下载: 全尺寸图片幻灯片

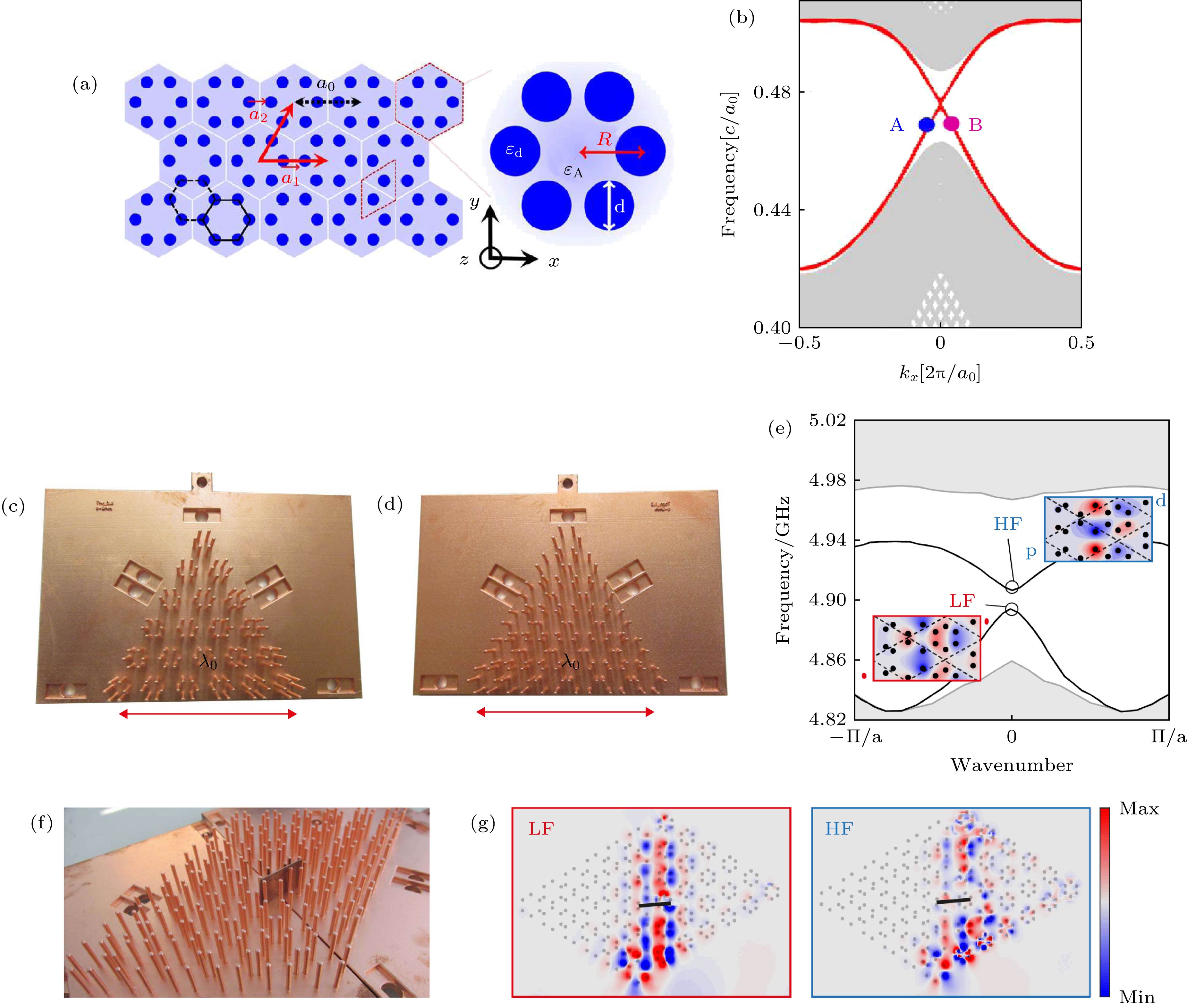
图 5 人工表面等离激元VHE和QVH^[38,41,42]　(a)二维过渡金属二硫化物(TMDS)的示意图; (b)第一布里渊区TMDS的能带结构; (c)用于VHE的SSPPs结构; (d) SSPPs-VHE的模场扫描结果; (e)用于QVH的SSPPs结构; (f) SSPPs-QVH的模场测试结果

Fig. 5. Spoof plasmonic VHE and QVH^[38,41,42]: (a) Schematic of TMDS; (b) band structure of TMDS in the first Brillouin zone; (c) spoof-SPP platform for VHE; (d) experimental demonstration of spoof-SPP VHE; (e) spoof-SPP platform for QVH; (f) experimental demonstration of spoof-SPP QVH

下载: 全尺寸图片幻灯片

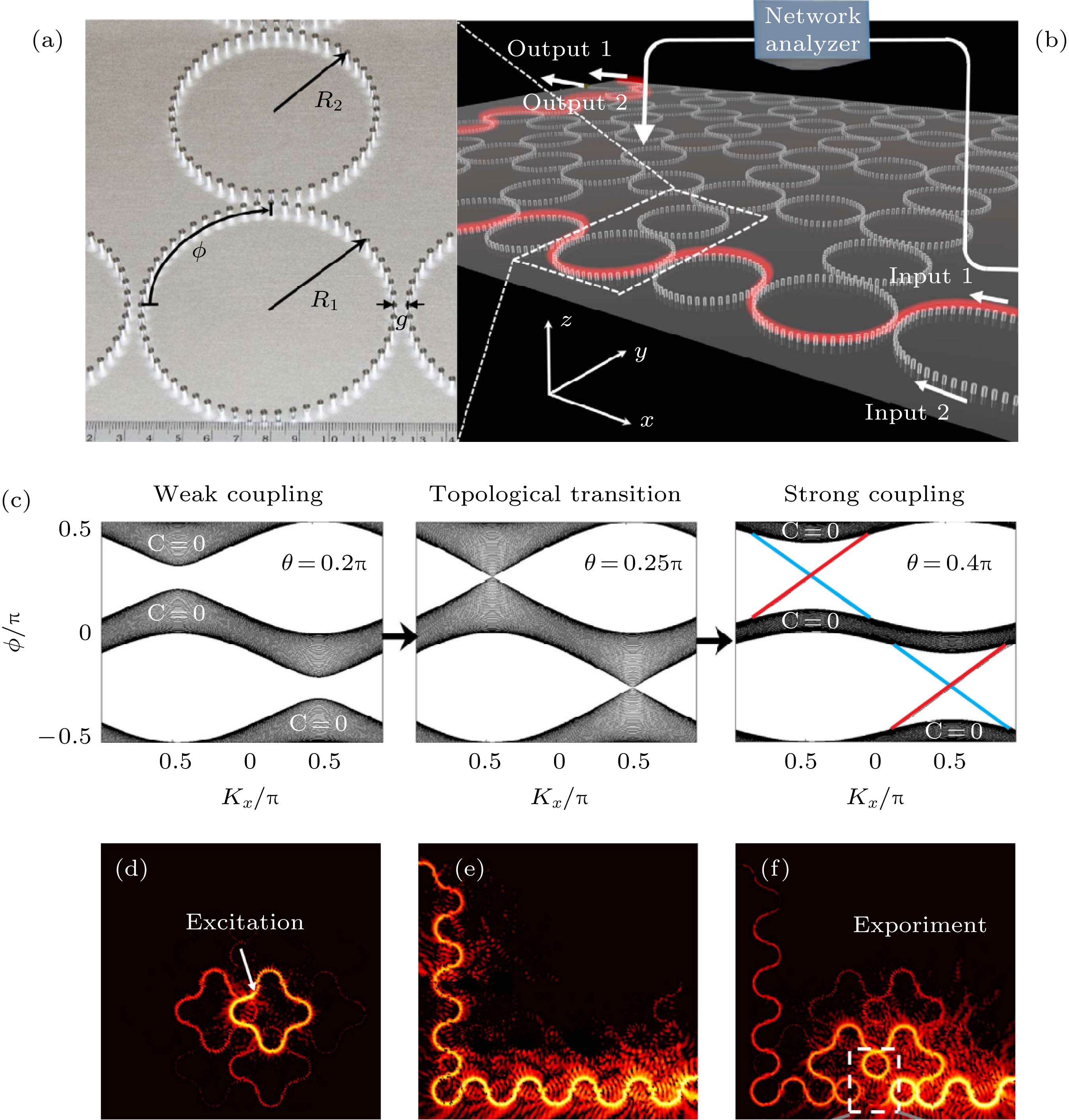
图 6 基于SSPPs结构的反常Floquet拓扑相^[14]　(a)人工表面等离激元环的照片; (b)实验中5 × 5点阵; (c)随着环间耦合的增加产生的拓扑相变; (d)当激励源频率为11.3 GHz时在阵列内观察到的局域模场; (e)在11.3 GHz频率观察到的边界态; (f)边界态绕过缺陷晶格传播

Fig. 6. Spoof plasmonic demonstration of the anomalous Floquet topological phase^[14]: (a) Photo of spoof plasmonic rings; (b) a 5 by 5 lattice inexperiment; (c) topological transition as the inter-ring coupling increases; (d) observed field pattern when the excitation is inside the bulk at frequency11.3 GHz; (e) observed edge state at frequency 11.3 GHz; (f) the edge state circumvents and tunnels through a defect lattice

下载: 全尺寸图片幻灯片

map

[1]	Wood R W 1902 The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science (Abingdon: Taylor & Francis) pp4–396
[2]	Pines D 1956 Rev. Mod. Phys. 28 184 Google Scholar
[3]	Ritchie R H 1957 Phys. Rev. 106 874 Google Scholar
[4]	Ritchie R H, Arakawa E, Cowan J, Hamm R 1968 Phys. Rev. Lett. 21 1530 Google Scholar
[5]	Cunningham S, Maradudin A, Wallis R 1974 Phys. Rev. B 10 3342 Google Scholar
[6]	Pendry J B, Martin-Moreno L, Garcia-Vidal F J 2004 Science 305 847 Google Scholar
[7]	Garcia-Vidal F J, Martin-Moreno L, Pendry J B 2005 J. Opt. A: Pure Appl. Opt 7 S97 Google Scholar
[8]	Qi X L, Zhang S C 2011 Rev. Mod. Phys. 83 54
[9]	Hasan M Z, Kane C L 2010 Rev. Mod. Phys. 82 3045 Google Scholar
[10]	Haldane F D M, Raghu S 2008 Phys. Rev. Lett. 100 013904 Google Scholar
[11]	Wang Z, Chong Y D, Joannopoulos J D, Soljacic M 2009 Nature 461 772 Google Scholar
[12]	Lu L, Joannopoulos J D, Soljačić M 2014 Nat. Photonics 8 821 Google Scholar
[13]	Chen W J, Jiang S J, Chen X D, Zhu B C, Zhou L, Dong J W, Chan C T 2014 Nat. Commun. 5 5782 Google Scholar
[14]	Gao F, Gao Z, Shi X H, Yang Z J, Lin X, Xu H Y, Joannopoulos J D, Soljacic M, Chen H S, Lu L, Chong Y D, Zhang B L 2016 Nat. Commun. 7 11619 Google Scholar
[15]	Cheng X J, Jouvaud C, Ni X, Mousavi S H, Genack A Z, Khanikaev A B 2016 Nat. Mater. 15 542 Google Scholar
[16]	Dong J W, Chen X D, Zhu H Y, Wang Y, Zhang X 2017 Nat. Mater. 16 298 Google Scholar
[17]	Gao F, Xue H R, Yang Z J, Lai K F, Yu Y, Lin X, Chong Y D, Shvets G, Zhang B L 2018 Nat. Phys. 14 140 Google Scholar
[18]	Gao W L, Lawrence M, Yang B A, Liu F, Fang F Z, Beri B, Li J S, Zhang S 2015 Phys. Rev. Lett. 114 037402 Google Scholar
[19]	Hafezi M, Mittal S, Fan J, Migdall A, Taylor J M 2013 Nat. Photonics 7 1001 Google Scholar
[20]	Khanikaev A B, Mousavi S H, Tse W K, Kargarian M, MacDonald A H, Shvets G 2013 Nat. Mater. 12 233 Google Scholar
[21]	Liang G, Chong Y 2013 Phys. Rev. Lett. 110 203904 Google Scholar
[22]	Ma T, Khanikaev A B, Mousavi S H, Shvets G 2015 Phys. Rev. Lett. 114 127401 Google Scholar
[23]	Ma T, Shvets G 2016 New J. Phys. 18 025012 Google Scholar
[24]	Noh J, Huang S, Chen K P, Rechtsman M C 2018 Phys. Rev. Lett. 120 063902 Google Scholar
[25]	Pasek M, Chong Y D 2014 Phys. Rev. B 89 075113 Google Scholar
[26]	Rechtsman M C, Zeuner J M, Plotnik Y, Lumer Y, Podolsky D, Dreisow F, Nolte S, Segev M, Szameit A 2013 Nature 496 196 Google Scholar
[27]	Wu L H, Hu X 2015 Phys. Rev. Lett. 114 223901 Google Scholar
[28]	Xiao M, Lin Q, Fan S H 2016 Phys. Rev. Lett. 117 057401 Google Scholar
[29]	Lu L, Joannopoulos J D, Soljacic M 2016 Nat. Phys. 12 626 Google Scholar
[30]	Jin D, Christensen T, Soljačić M, Fang N X, Lu L, Zhang X 2017 Phys. Rev. Lett. 118 245301 Google Scholar
[31]	Pan D, Yu R, Xu H, de Abajo F J G 2017 Nat. Commun. 8 1243 Google Scholar
[32]	Jung M, Fan Z, Shvets G 2018 Phys. Rev. Lett. 121 086807 Google Scholar
[33]	Gao Z, Gao F, Zhang Y M, Xu H Y, Luo Y, Zhang B L 2017 Adv. Mater. 29 1700018 Google Scholar
[34]	Murakami S, Nagaosa N, Zhang S C 2003 Science 301 1348 Google Scholar
[35]	Kane C L, Mele E J 2005 Phys. Rev. Lett. 95 226801 Google Scholar
[36]	Haldane F D M 1988 Phys. Rev. Lett. 61 2015 Google Scholar
[37]	Yves S, Fleury R, Berthelot T, Fink M, Lemoult F, Lerosey G 2017 Nat. Commun. 8 16023 Google Scholar
[38]	Xu X D, Yao W, Xiao D, Heinz T F 2014 Nat. Phys. 10 343 Google Scholar
[39]	Mak K F, McGill K L, Park J, McEuen P L 2014 Science 344 1489 Google Scholar
[40]	Ju L, Shi Z W, Nair N, Lv Y C, Jin C H, Velasco J, Ojeda-Aristizabal C, Bechtel H A, Martin M C, Zettl A, Analytis J, Wang F 2015 Nature 520 650 Google Scholar
[41]	Gao Z, Yang Z J, Gao F, Xue H R, Yang Y H, Dong J W, Zhang B L 2017 Phys. Rev. B 96 201402 Google Scholar
[42]	Wu X X, Meng Y, Tian J X, Huang Y Z, Xiang H, Han D Z, Wen W J 2017 Nat. Commun. 8 1304 Google Scholar
[43]	Yin X B, Ye Z L, Rho J, Wang Y, Zhang X 2013 Science 339 1405 Google Scholar
[44]	Kitagawa T, Berg E, Rudner M, Demler E 2010 Phys. Rev. B 82 235114 Google Scholar
[45]	Kitagawa T, Rudner M S, Berg E, Demler E 2010 Phys. Rev. A 82 033429 Google Scholar
[46]	Rudner M S, Lindner N H, Berg E, Levin M 2013 Phys. Rev. X 3 031005
[47]	Lohse M, Schweizer C, Price H M, Zilberberg O, Bloch I 2018 Nature 553 55 Google Scholar
[48]	Zilberberg O, Huang S, Guglielmon J, Wang M H, Chen K P, Kraus Y E, Rechtsman M C 2018 Nature 553 59 Google Scholar
[49]	Benalcazar W A, Bernevig B A, Hughes T L 2017 Science 357 61 Google Scholar
[50]	Khanikaev A B, Mousavi S H, Shvets G, Kivshar Y S 2010 Phys. Rev. Lett. 105 126804 Google Scholar
[51]	Leykam D, Chong Y D 2016 Phys. Rev. Lett. 117 143901 Google Scholar
[52]	Ni X, Purtseladze D, Smirnova D A, Slobozhanyuk A, Alù A, Khanikaev A B 2018 Sci. Adv. 4 eaap8802 Google Scholar
[53]	Yu N F, Wang Q J, Kats M A, Fan J A, Khanna S P, Li L H, Davies A G, Linfield E H, Capasso F 2010 Nat. Mater. 9 730 Google Scholar
[54]	Karl N J, McKinney R W, Monnai Y, Mendis R, Mittleman D M 2015 Nat. Photonics 9 717 Google Scholar
[55]	Ma J J, Karl N J, Bretin S, Ducournau G, Mittleman D M 2017 Nat. Commun. 8 729 Google Scholar
[56]	Grady N K, Heyes J E, Chowdhury D R, Zeng Y, Reiten M T, Azad A K, Taylor A J, Dalvit D A, Chen H T 2013 Science 340 1304 Google Scholar
[57]	Chen H T, O'hara J F, Azad A K, Taylor A J, Averitt R D, Shrekenhamer D B, Padilla W J 2008 Nat. Photonics 2 295 Google Scholar

[1]	王哲飞, 吴杰, 万发雨, 曾庆生, 侯建强, 傅佳辉, 吴群, 宋明歆, TayebA. Denidni. 基于类电磁诱导透明效应的极化转换滤波器. , 2024, 73(18): 188101. doi: 10.7498/aps.73.20240632
[2]	陈永强, 许光远, 王军, 方宇, 吴幸智, 丁亚琼, 孙勇. 基于非对称微波光子晶体的电磁二极管. , 2022, 71(3): 034701. doi: 10.7498/aps.71.20211291
[3]	宁仁霞, 黄旺, 王菲, 孙剑, 焦铮. 双明模耦合的双波段类电磁诱导透明研究. , 2022, 71(1): 014201. doi: 10.7498/aps.71.20211312
[4]	陈永强, 许光远, 王军, 方宇, 吴幸智, 丁亚琼, 孙勇. 基于非对称微波光子晶体的电磁二极管. , 2021, (): . doi: 10.7498/aps.70.20211291
[5]	王越, 冷雁冰, 王丽, 董连和, 刘顺瑞, 王君, 孙艳军. 基于石墨烯振幅可调的宽带类电磁诱导透明超材料设计. , 2018, 67(9): 097801. doi: 10.7498/aps.67.20180114
[6]	刘仿, 李云翔, 黄翊东. 基于双表面等离子激元吸收的纳米光刻. , 2017, 66(14): 148101. doi: 10.7498/aps.66.148101
[7]	郭畅, 张岩. 利用波矢滤波超表面实现超衍射成像. , 2017, 66(14): 147804. doi: 10.7498/aps.66.147804
[8]	张会云, 黄晓燕, 陈琦, 丁春峰, 李彤彤, 吕欢欢, 徐世林, 张晓, 张玉萍, 姚建铨. 基于石墨烯互补超表面的可调谐太赫兹吸波体. , 2016, 65(1): 018101. doi: 10.7498/aps.65.018101
[9]	吴青峻, 吴凡, 孙理斌, 胡晓琳, 叶鸣, 徐越, 史斌, 谢昊, 夏娟, 蒋建中, 张冬仙. 基于表面等离子激元的超薄金属减色滤波器的研究. , 2014, 63(20): 207801. doi: 10.7498/aps.63.207801
[10]	王五松, 张利伟, 冉佳, 张冶文. 微波频段表面等离子激元波导滤波器的实验研究. , 2013, 62(18): 184203. doi: 10.7498/aps.62.184203
[11]	丁敏, 薛晖, 吴博, 孙兵兵, 刘政, 黄志祥, 吴先良. 基于电磁超材料的两种等效参数提取算法的比较分析. , 2013, 62(4): 044218. doi: 10.7498/aps.62.044218
[12]	黄茜, 张德坤, 熊绍珍, 赵颖, 张晓丹. 降低表面等离子激元寄生吸收损失的途径研究. , 2012, 61(21): 217301. doi: 10.7498/aps.61.217301
[13]	黄茜, 熊绍珍, 赵颖, 张晓丹. 表面等离子激元非线性表面增强拉曼散射效应. , 2012, 61(15): 157801. doi: 10.7498/aps.61.157801
[14]	程用志, 聂彦, 龚荣洲, 郑栋浩, 范跃农, 熊炫, 王鲜. 基于超材料与电阻型频率选择表面的薄型宽频带吸波体的设计. , 2012, 61(13): 134101. doi: 10.7498/aps.61.134101
[15]	佟建波, 黄茜, 张晓丹, 张存善, 赵颖. 纳米Ag颗粒表面等离子激元对上转换材料光致发光性能影响的研究. , 2012, 61(4): 047801. doi: 10.7498/aps.61.047801
[16]	吴翔, 裴志斌, 屈绍波, 徐卓, 柏鹏, 王甲富, 王新华, 周航. 具有极化选择特性的超材料频率选择表面的设计. , 2011, 60(11): 114201. doi: 10.7498/aps.60.114201
[17]	郑俊娟, 孙刚. 嵌入电介质小球的金属薄片的电磁波透射特性. , 2010, 59(6): 4008-4013. doi: 10.7498/aps.59.4008
[18]	宋国峰, 汪卫敏, 蔡利康, 郭宝山, 王青, 徐云, 韦欣, 刘运涛. 表面等离子激元调制的亚波长束斑半导体激光器. , 2010, 59(7): 5105-5109. doi: 10.7498/aps.59.5105
[19]	付非亚, 陈微, 周文君, 刘安金, 邢名欣, 王宇飞, 郑婉华. 纳米三明治结构光子超材料中电磁场振荡行为研究. , 2010, 59(12): 8579-8583. doi: 10.7498/aps.59.8579
[20]	郑俊娟, 孙刚. 周期排列的电介质小球所诱发的金属-电介质表面上的表面等离子激元的光学性质. , 2005, 54(11): 5210-5217. doi: 10.7498/aps.54.5210

计量

文章访问数: 14606
PDF下载量: 655
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

拓扑表面等离激元