-
对非线性晶体参量下转换过程所产生的纠缠光子对的一路光子进行测量, “宣布”式地在另一路获得单光子, 是制备单光子源的一种重要途径. 其中, 核心的问题是如何得到较高的宣布效率. 本文以I类相位匹配偏硼酸钡 (β-BaB2O4, BBO)非线性晶体参量下转换过程中所产生的偏振纠缠光子对为例, 通过研究其纠缠特性来对宣布效率与宣布测量基选择的相关性进行理论分析. 进而, 利用光纤偏振分束器和三个单光子探测器搭建的扩展型Hanbury Brown-Twiss实验装置, 实现了宣布效率的测量. 实验结果表明, 宣布效率确实与宣布基选择有关: 对本系统的纠缠光子源而言, 采用
$|+/-\rangle$ 偏振宣布基所得到的宣布效率比采用$|H/V\rangle$ 偏振宣布基所得到的宣布效率提高了大约4%.The method by measuring one photon of an entangled two-photon pair to simultaneously herald another photon as the single photon, is one of the important ways to prepare the desired single-photon source. However, achieving high herald efficiency is still an open problem. In this paper, with the polarization entangled photon pairs generated by the parametric down-conversion process in the I-type phase-matched BBO (β-BaB2O4) nonlinear crystal, we investigate how the herald efficiency of the single-photon along the ideal path depends on the selection of the heralded basis of the photon in the signal path. An extended Hanbury-Brown-Twiss experimental system is built with a fiber polarizing beam splitter and three single-photon detectors, to experimentally measure the herald efficiency of the heralded single-photon source. Our results show that with the present polarization entangled-photon system whose quality is relatively low, the herald efficiency with the $|+/-\rangle$ heralded basis is enhanced 4% compared with that with the$|H/V\rangle$ heralded basis.-
Keywords:
- parametric down conversion /
- entangled photon pairs /
- heralded single photon source /
- heralded efficiency
[1] Michler P, Kiraz A, Becher C, Schoenfeld W V, Petroff P M, Zhang L, Hu E, Imamoglu A 2000 Science 290 2282
Google Scholar
[2] Brunel C, Lounis B, Tamarat P, Orrit M 1999 Phys. Rev. Lett. 83 2722
Google Scholar
[3] Kurtsiefer C, Mayer S, Zarda P, Weinfurter H 2000 Phys. Rev. Lett. 85 290
Google Scholar
[4] Soujaeff A, Nishioka T, Hasegawa T, Takeuchi S, Tsurumaru T, Sasaki K, Matsui M 2007 Opt. Express 15 726
Google Scholar
[5] Sanaka K, Jennewein T, Pan J W, Resch K, Zeilinger A 2004 Phys. Rev. Lett. 92 017902
Google Scholar
[6] Klyshko D N, Penin A N, Polkovnikov B F 1970 JETP Lett. 11 05
[7] Kwiat P G, Mattle K, Weinfurter H, Zeilinger A 1995 Phys. Rev. Lett. 75 4337
Google Scholar
[8] Kwiat P G, Waks E, White A G, Appelbaum I, Eberhard P H 1999 Phys. Rev. A 60 R773
Google Scholar
[9] Jeffrey E, Peters N A, Kwiat P G 2004 New J. Phys. 6 100
Google Scholar
[10] Fasel S, Alibart O, Tanzilli S, Baldi P, Beveratos A, Gisin N, Zbindenet H 2004 New J. Phys. 6 163
Google Scholar
[11] Pittman T B, Jacobs B C, Franson J D 2005 Opt. Commun. 246 545
Google Scholar
[12] Ramelow S, Mech A, Giustina M, Gröblacher S, Wieczorek W, Beyer J, Lita A, Calkins B, Gerrits T, Nam S W, Zeilinger A, Ursin R 2013 Opt. Express 21 6707
Google Scholar
[13] Krapick S, Herrmann H, Quiring V, Brecht B, Suche H, Silberhorn Ch 2013 New J. Phys. 15 033010
Google Scholar
[14] Montaut N, Sansoni L, Meyer-Scott E, Ricken R, Quiring V, Herrmann H, Silberhorn C 2017 Phys. Rev. Appl. 8 024021
Google Scholar
[15] Cui L, Li X Y, Fan H Y, Yang L, Ma X X 2009 Chin. Phys. Lett. 26 044209
Google Scholar
[16] Ou Z Y, Wang L J, Mandel L 1990 J. Opt. Soc. Am. B 7 211
[17] 郭伟杰, 樊代和, 韦联福 2013 中国科学: 物理学 力学 天文学 43 948
Guo W J, Fan D H, Wei L F 2013 Sci. Sin.-Phys. Mech. Astron. 43 948
[18] Wang Y, Fan D H, Guo W J, Wei L F 2015 Chin. Phys. B 24 084203
Google Scholar
[19] 兰豆豆, 郭晓敏, 彭春生, 姬玉林, 刘香莲, 李璞, 郭龑强 2017 66 120502
Google Scholar
Lan D D, Gao X M, Peng C S, Ji Y L, Liu X L, Li P, Guo Y Q 2017 Acta Phys. Sin. 66 120502
Google Scholar
[20] Kimble H J, Dagenais M, Mandel L 1997 Phys. Rev. Lett. 39 691
[21] Genty G, Surakka M, Turunen J, Ari T 2010 Opt. Lett. 35 3057
Google Scholar
[22] Li G, Zhang T C, Li Y, Wang J 2005 Phys. Rev. A 71 023807
Google Scholar
[23] Thorn J J, Neel M S, Donato V W, Bergreen G S, Davies R E, Beck M 2004 Am. J. Phys. 72 1210
Google Scholar
[24] Beck M 2007 J. Opt. Soc. Am. B 24 2972
Google Scholar
[25] Brida G, Degiovanni I P, Genovese M, Migdall A, Piacentini F, Polyakov S V, Berchera I R 2011 Opt. Express 19 1484
Google Scholar
-
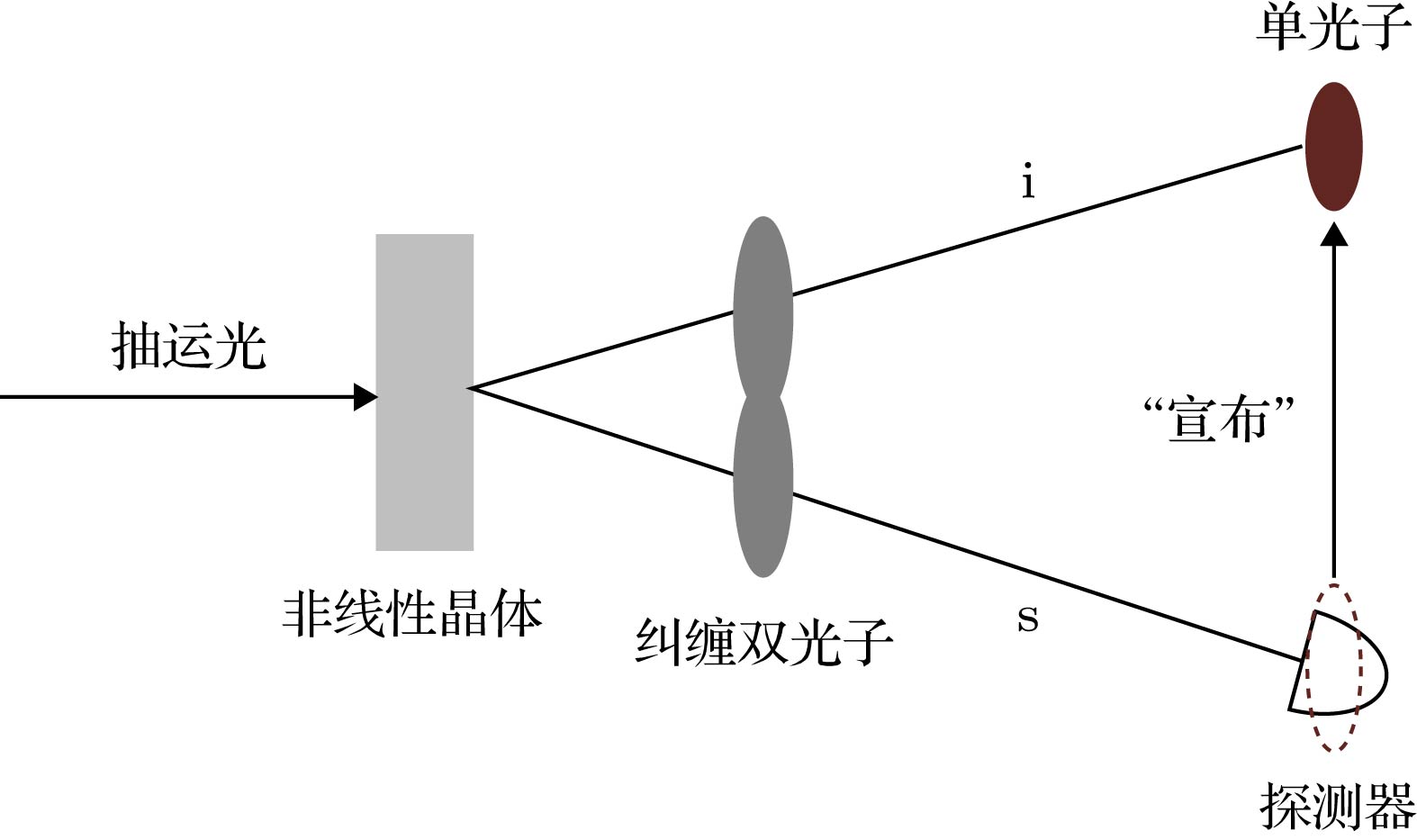
图 1 利用纠缠光子对制备宣布式单光子源的原理示意图 激光抽运非线性晶体使其发生参量下转换, 产生纠缠的信号光(s, 图中下面一路)和闲置光(i, 图中上面一路); 探测信号光子从而将其孪生的闲置光子“宣布”为单光子
Fig. 1. Schematic diagram of the preparation of a heralded single photon source using entangled photons. The laser pumped nonlinear crystal causes parametric down-conversion to produce entangled signal light (s, the lower path in the figure) and idle light (i, the upper one in the figure); Detecting signal photons to “herald” the twinned photon into single photons.
图 2 利用I类BBO非线性晶体产生纠缠光子对的原理简图 圆锥表示光场分布, 与上下光路的交叉点为光子信号的采集点, 所采集的光子偏振为
$|HH\rangle$ 或者为$|VV\rangle$ Fig. 2. Schematic diagram of generating entangled photon pairs using class I BBO nonlinear crystals. The cone represents the light field distribution, and the intersection with the upper and lower light paths is the collection point of the photon signal, and the acquired photon polarization is
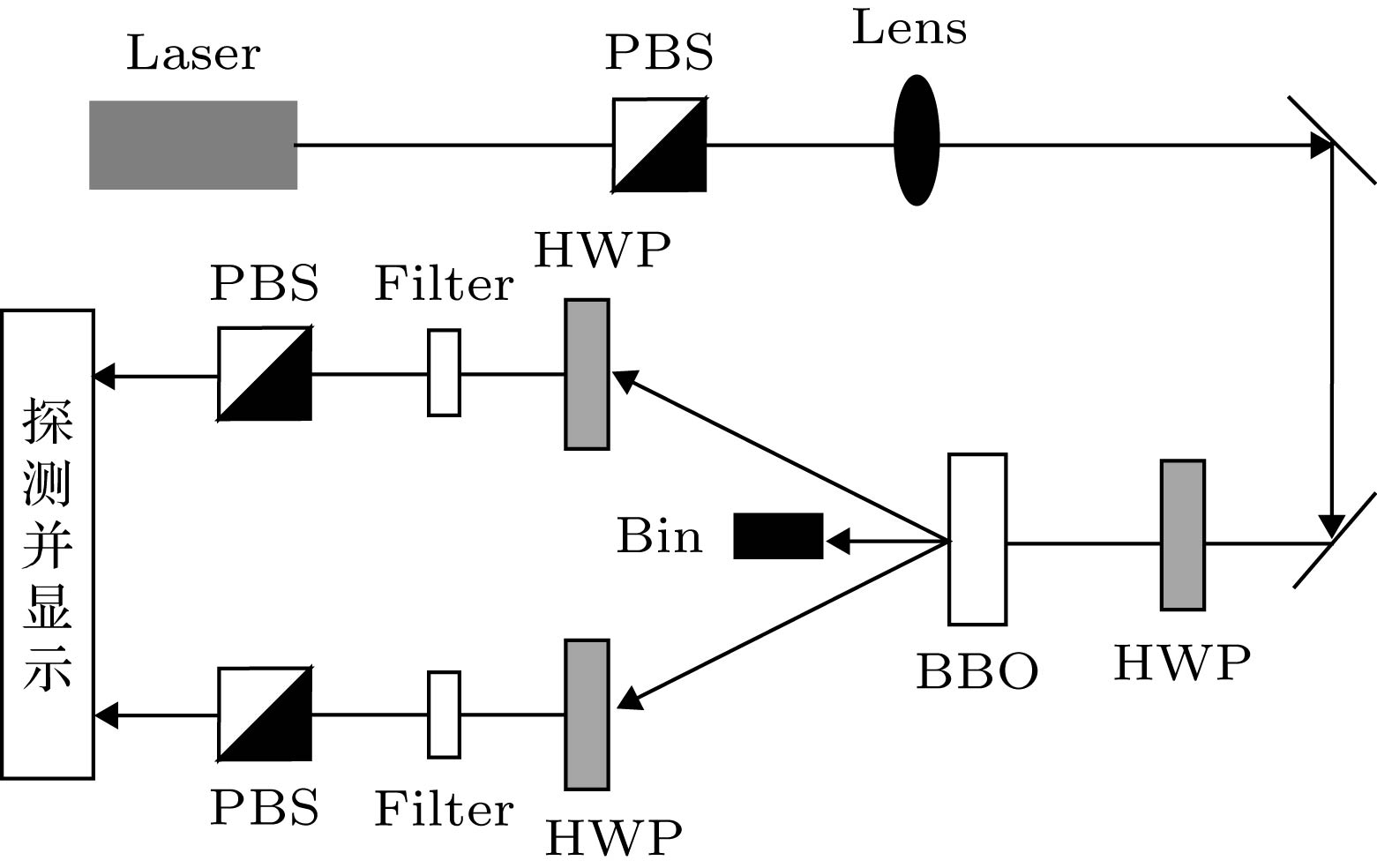
$|HH\rangle$ or$|VV\rangle$ .
图 3 纠缠光子对偏振关联测量原理图 透镜(Lens)之前的极化分束器(PBS)的作用是滤掉水平偏振的激光(取其反射光进入透镜, 这里省略了反射光路), BBO晶体之前的半波片(HWP)用于产生偏振叠加抽运光, BBO用于产生纠缠双光子, 半波片、滤波片(Filter)、PBS和探测器构成光子的偏振探测系统, 符合计数器记录并显示两个单光子探测器的符合信号
Fig. 3. Schematic diagram of entangled photon pair polarization correlation measurement. The polarized beam splitter (PBS) before Lens is used to filter out horizontally polarized lasers, the half-wave plate (HWP) before the BBO crystal is used to generate polarized superimposed pump light, and BBO is used to generate entangled photon pairs. A half-wave plate, a filter, a PBS, and a detector constitute a photon polarization detection system, coincidence counter records and display the coincidence signals for two single photon detectors.
图 4 纠缠光子偏振关联的实验测量结果
Fig. 4. Experimental measurement results of the polarization correlations for entangled photon-pairs.
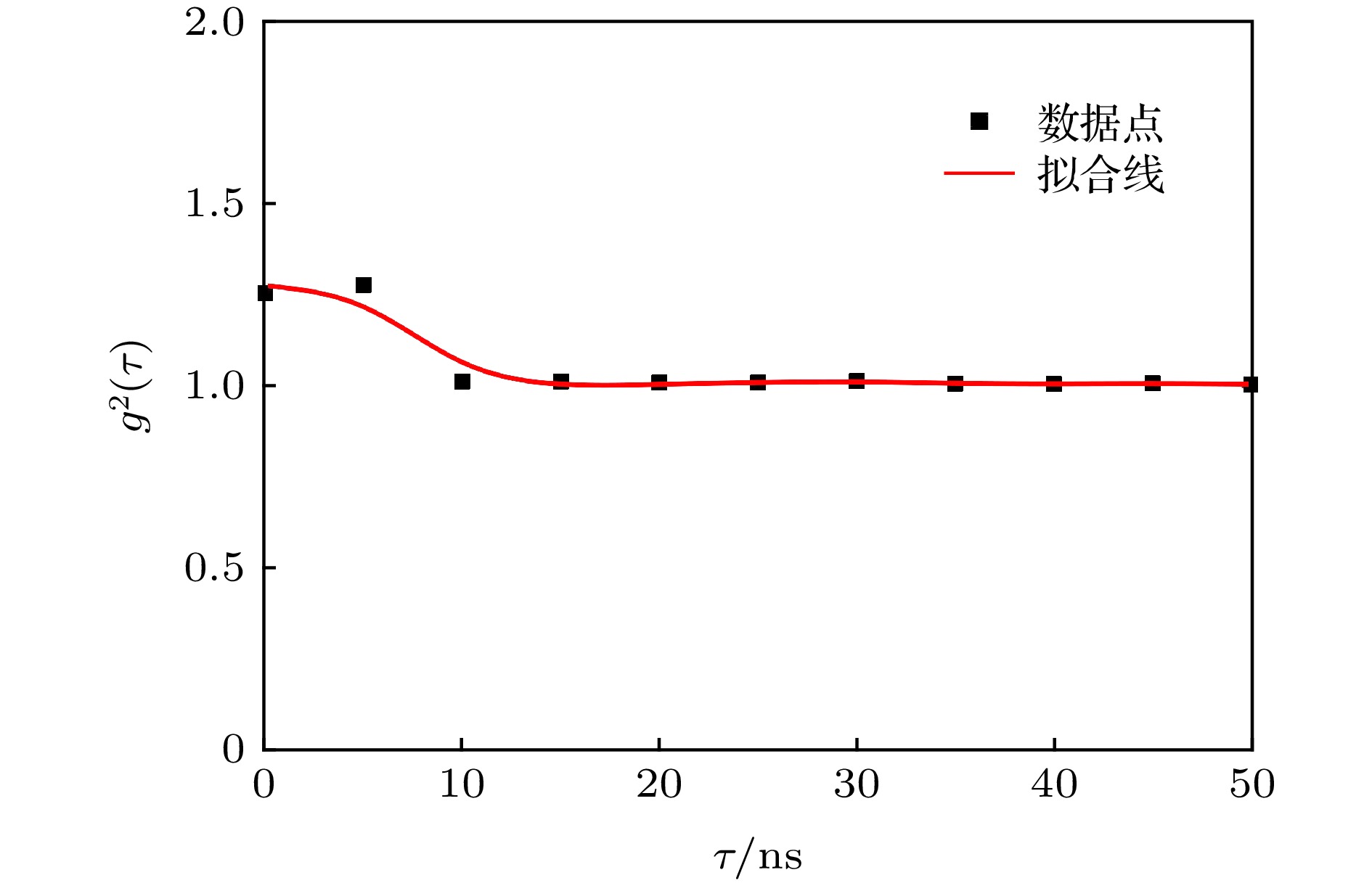
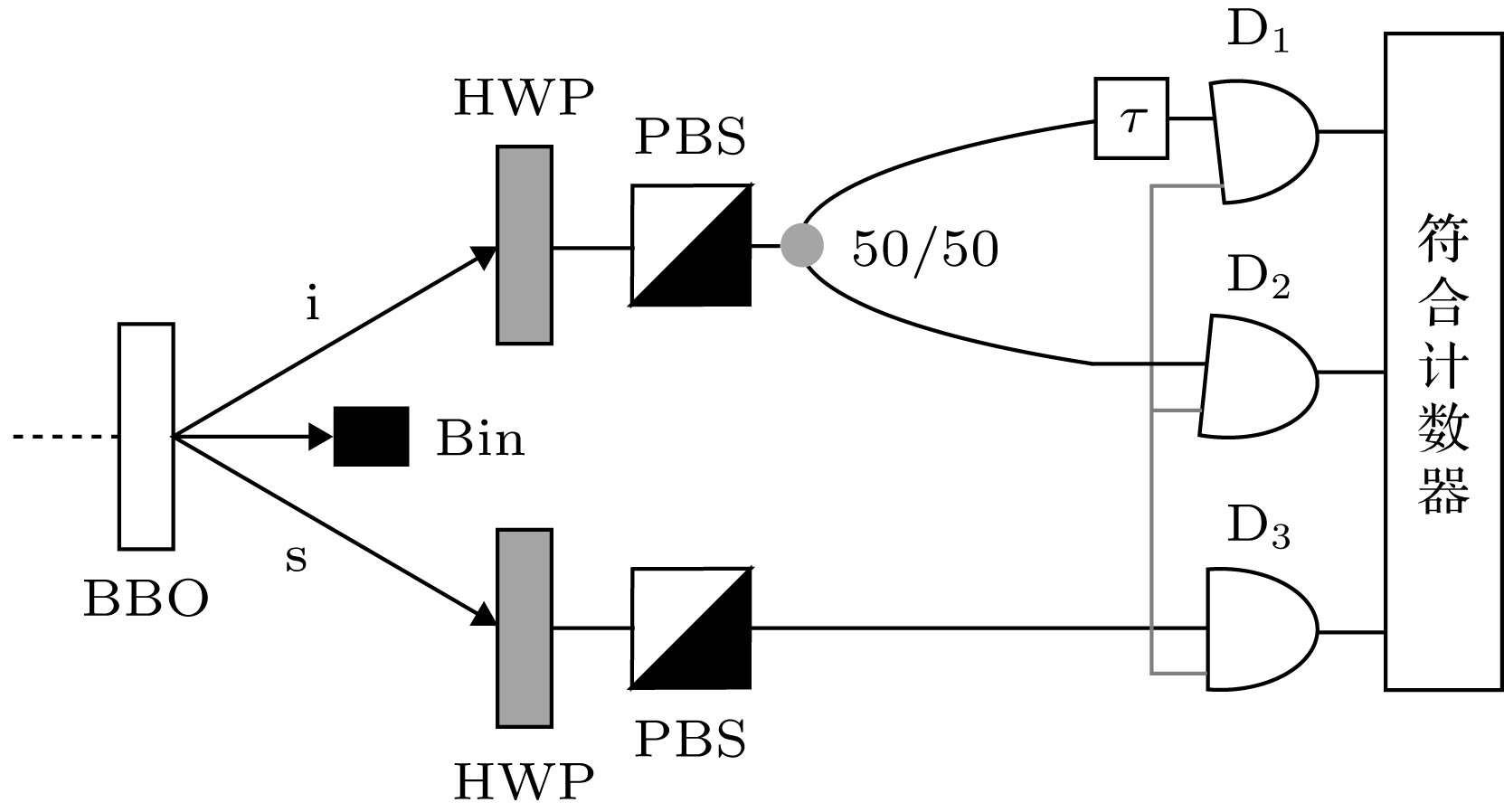
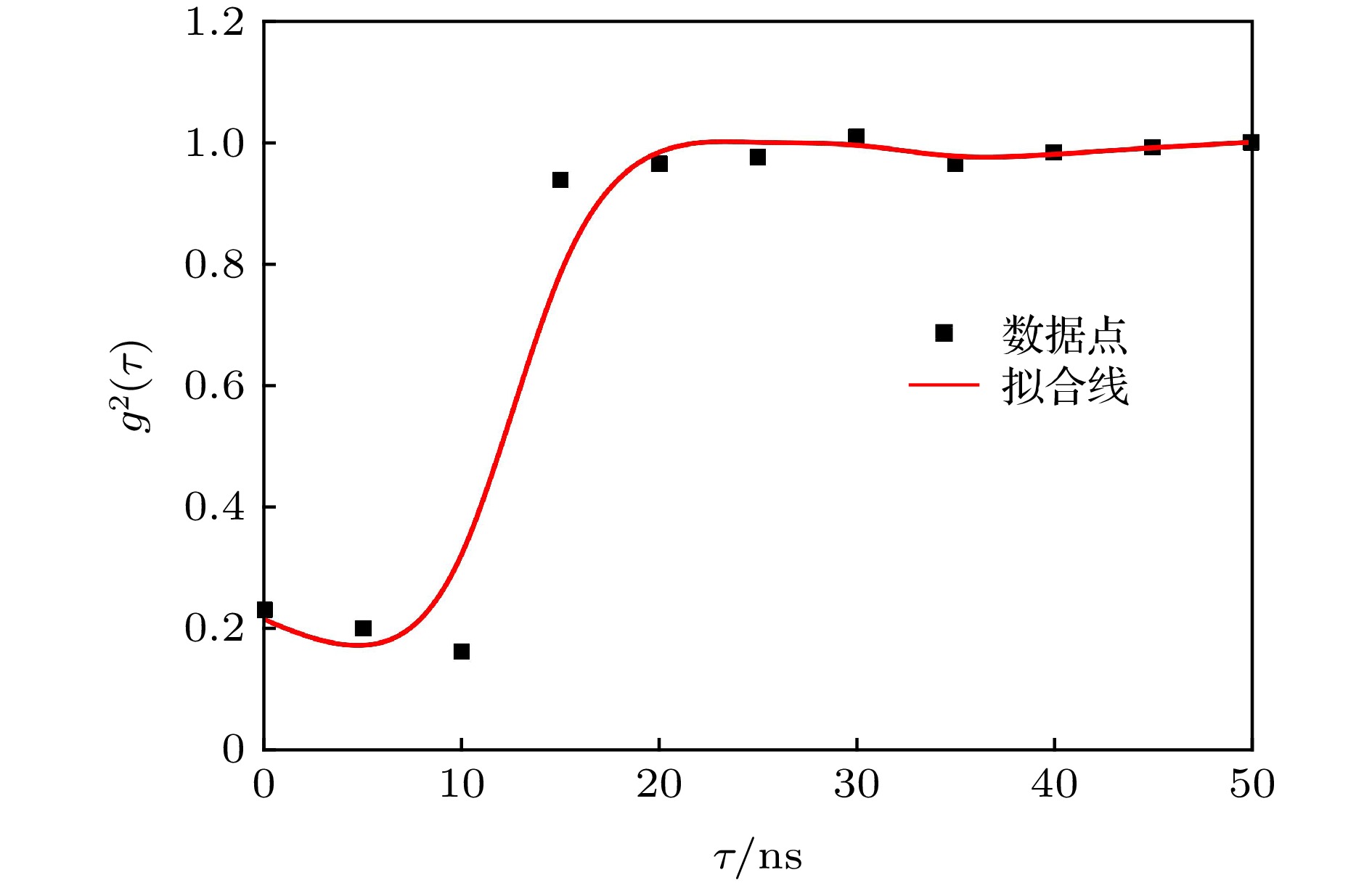
图 5 HBT实验原理图 一束光通过50/50分束器后被均分为两路(其中一路经过延时
$\tau$ ), 最后两路信号分别被两个探测器所探测, 其同时性由符合计数特性表征Fig. 5. Schematic diagram of the HBT experiment, wherein a laser beam is splitted, after a 50/50 beam splitter, into two paths; one of them is delayed by a duration
$\tau$ , then the signals of the two paths are detected by the two detectors, respectively. The simultaneity of the detected signals is characterized by the coincidence countings.
图 6 不对信号光宣布而直接测量闲置光场二阶相干度的实验结果
Fig. 6. The measured second-order coherence for the idle light field without being heralded by the signal light.
图 7 宣布式单光子场的二阶关联函数实验测量光路图
Fig. 7. Optical path system for measuring the heralded efficiency of the heralded single photons.
图 8 宣布式单光子场二阶相干度测量结果
Fig. 8. Measurement results of second-order coherence of the single photon field.
表 1 不同延时的符合计数结果
Table 1. Coincidence results for different delays.
延时/ns 0 5 10 15 20 25 30 35 40 45 50 符合计数 7905 8043 6369 6379 6351 6349 6377 6328 6322 6339 6318 
下载: 导出CSV
表 2 不同测量基下的三个单光子探测器的符合计数结果
Table 2. Coincidence results of three single-photon detectors under different measurement bases.
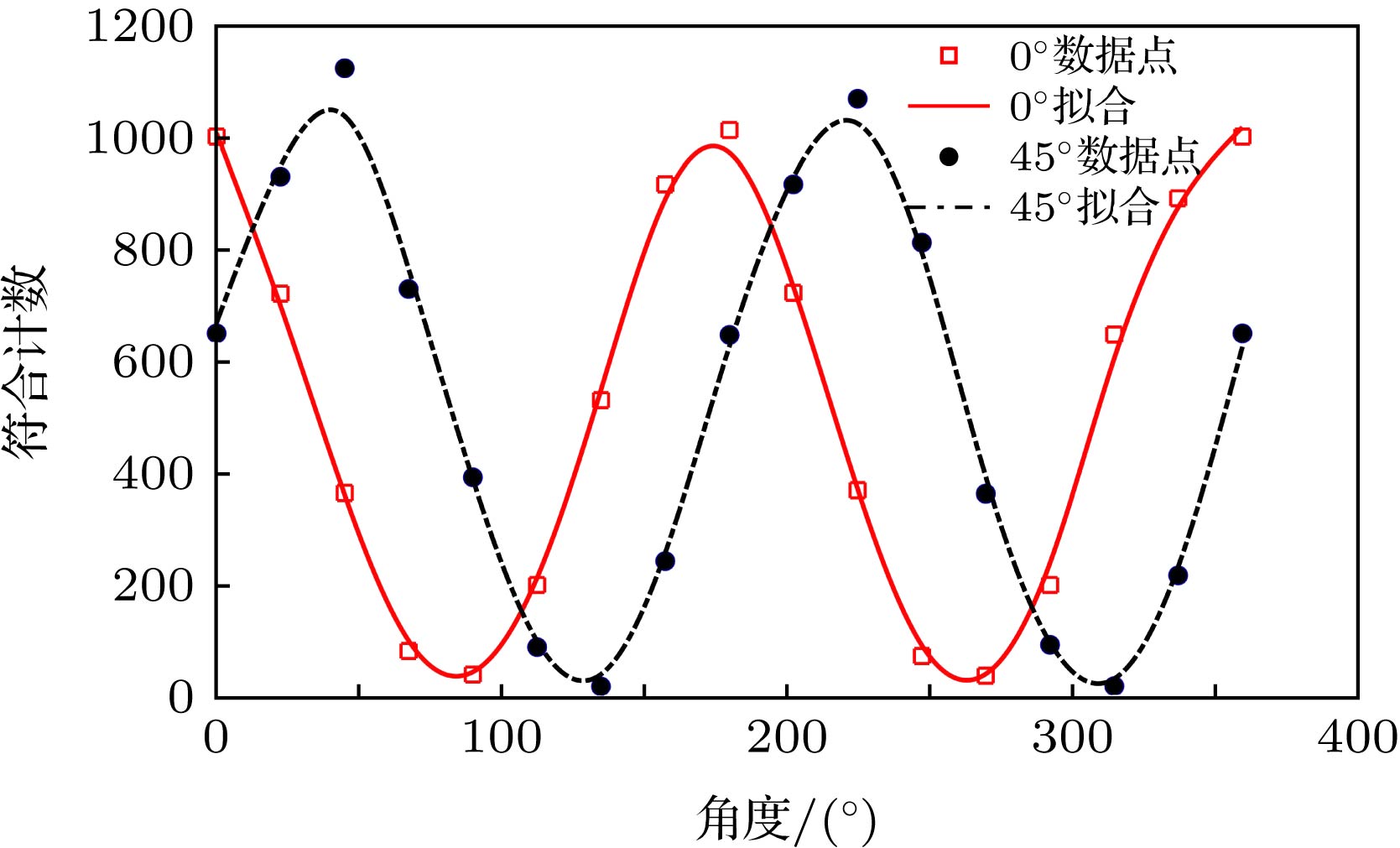
符合通道 $N_{13}$ $N_{23}$ $N_{123}$ $|H\rangle|H\rangle$ 583 607 111 $|+\rangle|+\rangle$ 693 730 158
下载: 导出CSV
表 3 信号光不同偏振测量基下三个探测器的符合计数实验测量结果
Table 3. Coincidence countings of three single-photon detectors for different polarization measurements.
信号光路
偏振状态信号光路光子
计数率闲置光场所处的
偏振态符合计数 $|H\rangle$ 6859 $|H\rangle$ 1142 $|V\rangle$ 54 $|V\rangle$ 6945 $|V\rangle$ 1137 $|H\rangle$ 39 $|+\rangle$ 7492 $|+\rangle$ 1416 $|-\rangle$ 12 $|-\rangle$ 6277 $|-\rangle$ 1178 $|+\rangle$ 15
下载: 导出CSV
-
[1] Michler P, Kiraz A, Becher C, Schoenfeld W V, Petroff P M, Zhang L, Hu E, Imamoglu A 2000 Science 290 2282
Google Scholar
[2] Brunel C, Lounis B, Tamarat P, Orrit M 1999 Phys. Rev. Lett. 83 2722
Google Scholar
[3] Kurtsiefer C, Mayer S, Zarda P, Weinfurter H 2000 Phys. Rev. Lett. 85 290
Google Scholar
[4] Soujaeff A, Nishioka T, Hasegawa T, Takeuchi S, Tsurumaru T, Sasaki K, Matsui M 2007 Opt. Express 15 726
Google Scholar
[5] Sanaka K, Jennewein T, Pan J W, Resch K, Zeilinger A 2004 Phys. Rev. Lett. 92 017902
Google Scholar
[6] Klyshko D N, Penin A N, Polkovnikov B F 1970 JETP Lett. 11 05
[7] Kwiat P G, Mattle K, Weinfurter H, Zeilinger A 1995 Phys. Rev. Lett. 75 4337
Google Scholar
[8] Kwiat P G, Waks E, White A G, Appelbaum I, Eberhard P H 1999 Phys. Rev. A 60 R773
Google Scholar
[9] Jeffrey E, Peters N A, Kwiat P G 2004 New J. Phys. 6 100
Google Scholar
[10] Fasel S, Alibart O, Tanzilli S, Baldi P, Beveratos A, Gisin N, Zbindenet H 2004 New J. Phys. 6 163
Google Scholar
[11] Pittman T B, Jacobs B C, Franson J D 2005 Opt. Commun. 246 545
Google Scholar
[12] Ramelow S, Mech A, Giustina M, Gröblacher S, Wieczorek W, Beyer J, Lita A, Calkins B, Gerrits T, Nam S W, Zeilinger A, Ursin R 2013 Opt. Express 21 6707
Google Scholar
[13] Krapick S, Herrmann H, Quiring V, Brecht B, Suche H, Silberhorn Ch 2013 New J. Phys. 15 033010
Google Scholar
[14] Montaut N, Sansoni L, Meyer-Scott E, Ricken R, Quiring V, Herrmann H, Silberhorn C 2017 Phys. Rev. Appl. 8 024021
Google Scholar
[15] Cui L, Li X Y, Fan H Y, Yang L, Ma X X 2009 Chin. Phys. Lett. 26 044209
Google Scholar
[16] Ou Z Y, Wang L J, Mandel L 1990 J. Opt. Soc. Am. B 7 211
[17] 郭伟杰, 樊代和, 韦联福 2013 中国科学: 物理学 力学 天文学 43 948
Guo W J, Fan D H, Wei L F 2013 Sci. Sin.-Phys. Mech. Astron. 43 948
[18] Wang Y, Fan D H, Guo W J, Wei L F 2015 Chin. Phys. B 24 084203
Google Scholar
[19] 兰豆豆, 郭晓敏, 彭春生, 姬玉林, 刘香莲, 李璞, 郭龑强 2017 66 120502
Google Scholar
Lan D D, Gao X M, Peng C S, Ji Y L, Liu X L, Li P, Guo Y Q 2017 Acta Phys. Sin. 66 120502
Google Scholar
[20] Kimble H J, Dagenais M, Mandel L 1997 Phys. Rev. Lett. 39 691
[21] Genty G, Surakka M, Turunen J, Ari T 2010 Opt. Lett. 35 3057
Google Scholar
[22] Li G, Zhang T C, Li Y, Wang J 2005 Phys. Rev. A 71 023807
Google Scholar
[23] Thorn J J, Neel M S, Donato V W, Bergreen G S, Davies R E, Beck M 2004 Am. J. Phys. 72 1210
Google Scholar
[24] Beck M 2007 J. Opt. Soc. Am. B 24 2972
Google Scholar
[25] Brida G, Degiovanni I P, Genovese M, Migdall A, Piacentini F, Polyakov S V, Berchera I R 2011 Opt. Express 19 1484
Google Scholar
下载:
计量
- 文章访问数: 9926
- PDF下载量: 147
- 被引次数: 0
