-
采用非平衡分子动力学方法研究了环状聚合物及其对应的线性链熔体在启动剪切场下的结构与流变特性. 模拟结果显示: 低剪切速率下(
$\dot \gamma < 1 \times {10^{ - 4}}{\tau ^{ - 1}}$ )环状链分子体系相比于同分子量的线性链体系并没有出现明显的过冲现象. 该结果表明, 在启动剪切场下环状分子与其对应的线性链相比较表现出了更弱的分子形变, 同时模拟结果也与最近实验观察的结果一致. 为了进一步探究这种现象背后的分子机理, 在分子层面统计了不同流场强度下, 链段的长度和取向角分布随着应变的演化, 统计结果证明了环状聚合物分子链段弱的形变是导致其弱的剪切变稀和峰值应变的主要因素. 本文还给出了过冲点和稳态在不同剪切速率下环状分子与其对应的线性链的流变特性(过冲应变、最大应力、最大黏性和稳态黏性)、结构和取向参数与维森伯格数(WiR)所满足的标度关系.We analyze the structure and rheological properties of ring and linear polymers under shear byusing the non-equilibrium molecular dynamics simulation. The simulation results show that compared with the ring chains, the linear polymers do not present prominent stress over shoot phenomenon. Since the overshoot reflects the maximum flow-induced deformation of the polymer, this qualitative observation already implies that the ring experience less deformation than its linear precursor in simple shear flow. This is consistent with the recent experimental result. In order to further study the molecular mechanism of this phenomenon, the segmental structure and orientation angle distribution as a function of strain under the different Weissenberg numbers are given in this study. The weak overshoot of the stretching of the ring polymers proves that the weak shear thinning and peak strain are due to the weak deformation of the segment chain of the ring in the shear flow. The rheological properties of linear and ring system are extracted from the stress-strain curves, can be used further to analyze the data. The peak strain γmax as afunction of WiR follows a power-law with an exponent of 0.3 for linear polymer at WiR>1, however, for the ring system thepeak strain follows a power-law with an exponent of 0.1. The parameter ηmax/ηsteady is also the measure of the effective chain deformation at a steady state. The data show its progressive increase with WiR increasing, and follows a power-law with a scaling slop of 0.13 and 0.08 for linear and ring polymers, respectively. The peak stress σmax as a function of WiR is also extracted from stress-strain curve. The two investigated systems both obey the scaling law with an exponent of 0.5. The normalized steady-state shear viscosity obeys a shear thinning slop of –0.86 for the linear polymer, the ring polymer obeysa shear thinning slop of –0.4. According to the gyration tensor and orientation angle, the power-law relationship between stretching and orientation is also given in this work.[1] Li Y, Hsiao K W, Brockman C A, Yates D Y, Robertson-Anderson R M, Kornfield J A, San Francisco M J, Schroeder C M, McKenna G B 2015 Macromolecules 48 5997
Google Scholar
[2] Sanchez T, Kulic I M, Dogic Z 2010 Phys. Rev. Lett. 104 098103
Google Scholar
[3] Micheletti C, Orlandini E 2012 Macromolecules 45 2113
Google Scholar
[4] Kapnistos M, Lang M, Vlassopoulos D, Pyckhout-Hintzen W, Richter D, Cho D, Chang T, Rubinstein M 2008 Nature Mater. 7 997
Google Scholar
[5] Klein J 1986 Macromolecules 19 105
Google Scholar
[6] Halverson J D, Grest G S, Grosberg A Y, Kremer K 2012 Phys. Rev. Lett. 108 038301
Google Scholar
[7] Hernández Cifre J G, Pamies R, López Martínez M C, García de la Torre J 2005 Polymer 46 267
Google Scholar
[8] Yan Z C, Costanzo S, Jeong Y, Chang T, Vlassopoulos D 2016 Macromolecules 49 1444
Google Scholar
[9] Chen W, Zhang K, Liu L, Chen J, Li Y, An L 2017 Macromolecules 50 1236
Google Scholar
[10] Chen W, Zhao H, Liu L, Chen J, Li Y, An L 2015 Soft Matter 11 5265
Google Scholar
[11] Rubinstein M 1986 Phy. Rev. Lett. 57 3023
Google Scholar
[12] Nechaev S K, Semenov A N, Koleva M K 1987 Physica A: Statist. Mech. Appl. 140 506
Google Scholar
[13] Chen W, Li Y, Zhao H, Liu L, Chen J, An L 2015 Polymer 64 93
Google Scholar
[14] Cao J, Likhtman A E 2015 ACS Macro. Lett. 4 1376
Google Scholar
[15] Luo C, Kröger M, Sommer J U 2017 Polymer 109 71
Google Scholar
[16] Kremer K, Grest G S 1990 J. Chem. Phys. 92 5057
Google Scholar
[17] Wang Z, Likhtman A E, Larson R G 2012 Macromolecules 45 3557
Google Scholar
[18] McLeish T C B 2002 Adv. Phys. 51 1379
Google Scholar
[19] Cao J, Likhtman A E 2012 Phy. Rev. Lett. 108 028302
Google Scholar
[20] DoiY, Matsubara K, Ohta Y, Nakano T, Kawaguchi D, Takahashi Y, Takano A, Matsushita Y 2015 Macromolecules 48 3140
Google Scholar
[21] Boukany P E, Wang S Q, Wang X 2009 J. Rheol. 53 617
Google Scholar
[22] Jeong S, Kim J M, Baig C 2017 Macromolecules 50 3424
Google Scholar
-
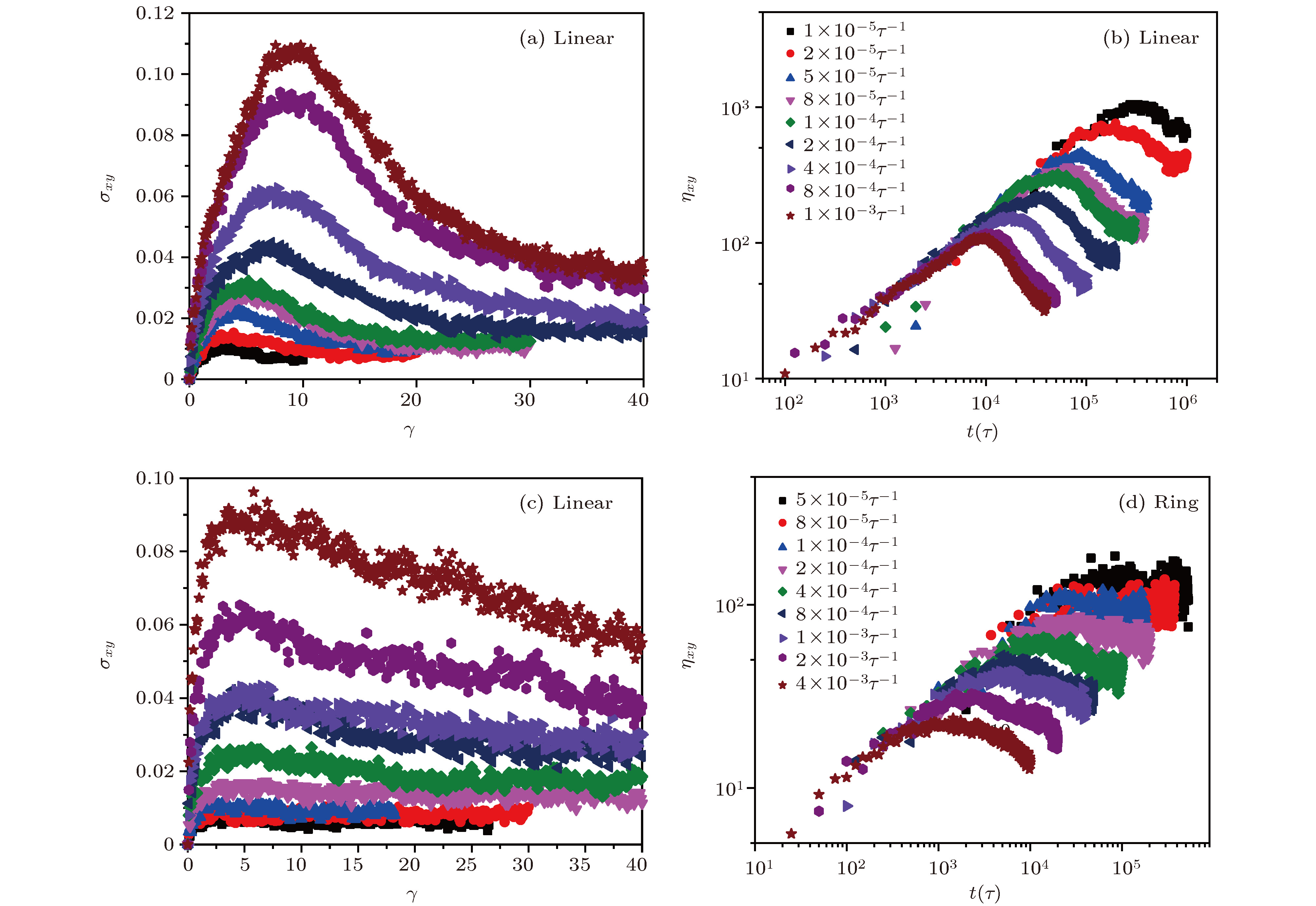
图 2 (a), (b)线性链体系对应的应力随着应变及剪切黏性随着时间的演化过程；(c), (d)环状链体系对应的应力随着应变及剪切黏性随着时间的演化过程
Fig. 2. (a), (b) Stress-strain and nonlinear startup shear viscosity as function of strain and time for linear polymers, respectively; (c), (d) stress-strain and nonlinear startup shear viscosity as function of strain and time for ring polymers, respectively.
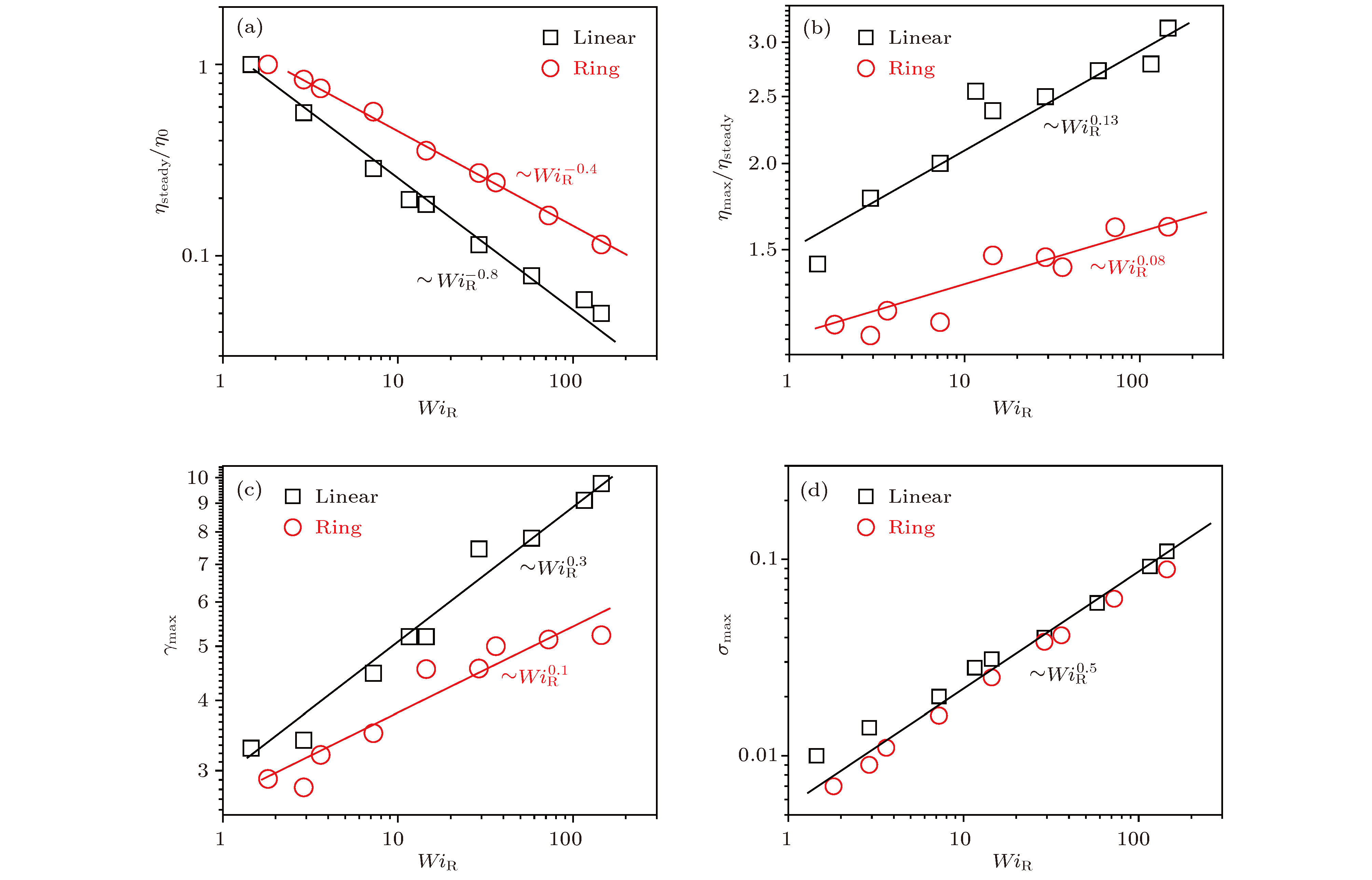
图 3 不同流场强度下线性链及其环状链的归一化稳态黏性
${\eta _{{\rm{steady}}}}/{\eta _0}$ (a), 最大黏性和稳态黏性比值${\eta _{\max }}/{\eta _{{\rm{steady}}}}$ (b), 峰应变${\gamma _{\max }}$ (c) 和最大应力${\sigma _{\max }}$ (d)随着$W{i_{\rm{R}}}$ 的变化Fig. 3. (a) Evolution of steady viscosity normalized with the zero-shear viscosity
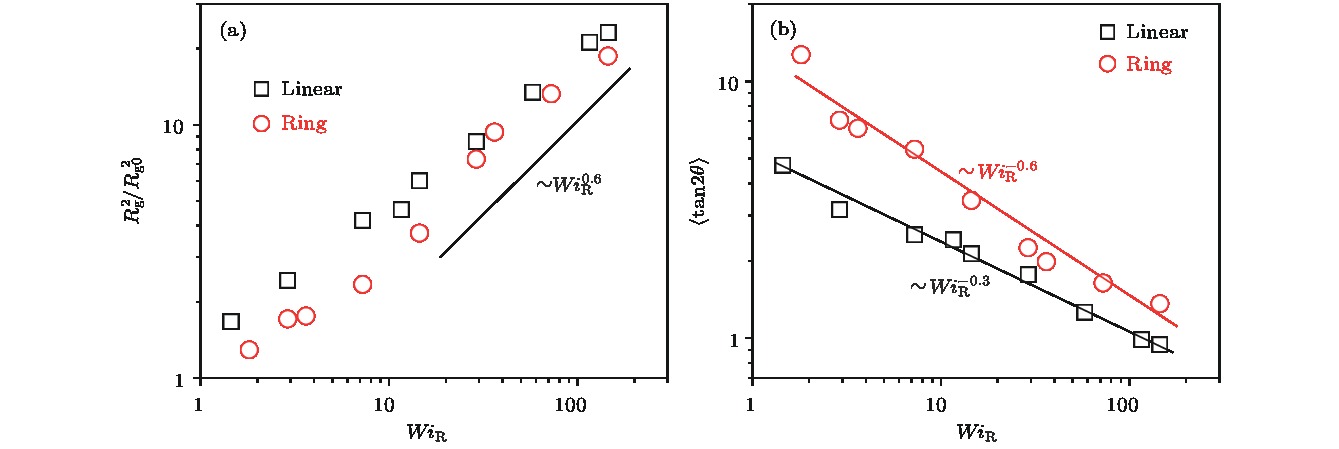
${\eta _{{\rm{steady}}}}/{\eta _0}$ , (b) maximum viscosity scaled with steady viscosity${\eta _{\max }}/{\eta _{{\rm{steady}}}}$ , (c) peak strains${\gamma _{\max }}$ and (d) peak shear stress${\sigma _{\max }}$ as a function of$W{i_{\rm{R}}}$ .
图 4 (a)线性链和环状链体系的
$\langle R_{\rm{g}}^2 \rangle/\langle {R_{{\rm{g}}0}^2}\rangle $ 随着$W{i_{\rm{R}}}$ 的变化；(b)线性链和环状链熔体的取向$\left\langle {\tan 2\theta } \right\rangle $ 随着$W{i_{\rm{R}}}$ 的变化Fig. 4. The
$\langle {R_{\rm{g}}^2}\rangle/\langle {R_{{\rm{g}}0}^2}\rangle $ (a) and$\left\langle {\tan 2\theta } \right\rangle $ (b) as a function of$W{i_{\rm{R}}}$ for linear and ring polymers.
图 5 不同
$W{i_{\rm{R}}}$ 下线性与环状分子链段长度分布随着应变的演化Fig. 5. Evolution of segmental length distribution of linear and ring polymers under the different
$W{i_{\rm{R}}}$ .
图 6 不同
$W{i_{\rm{R}}}$ 下线性与环状分子链段沿着剪切方向角分布随着应变的演化Fig. 6. Evolution of segmental angle distribution for linear and ring polymers under the different
$W{i_{\rm{R}}}$ . -
[1] Li Y, Hsiao K W, Brockman C A, Yates D Y, Robertson-Anderson R M, Kornfield J A, San Francisco M J, Schroeder C M, McKenna G B 2015 Macromolecules 48 5997
Google Scholar
[2] Sanchez T, Kulic I M, Dogic Z 2010 Phys. Rev. Lett. 104 098103
Google Scholar
[3] Micheletti C, Orlandini E 2012 Macromolecules 45 2113
Google Scholar
[4] Kapnistos M, Lang M, Vlassopoulos D, Pyckhout-Hintzen W, Richter D, Cho D, Chang T, Rubinstein M 2008 Nature Mater. 7 997
Google Scholar
[5] Klein J 1986 Macromolecules 19 105
Google Scholar
[6] Halverson J D, Grest G S, Grosberg A Y, Kremer K 2012 Phys. Rev. Lett. 108 038301
Google Scholar
[7] Hernández Cifre J G, Pamies R, López Martínez M C, García de la Torre J 2005 Polymer 46 267
Google Scholar
[8] Yan Z C, Costanzo S, Jeong Y, Chang T, Vlassopoulos D 2016 Macromolecules 49 1444
Google Scholar
[9] Chen W, Zhang K, Liu L, Chen J, Li Y, An L 2017 Macromolecules 50 1236
Google Scholar
[10] Chen W, Zhao H, Liu L, Chen J, Li Y, An L 2015 Soft Matter 11 5265
Google Scholar
[11] Rubinstein M 1986 Phy. Rev. Lett. 57 3023
Google Scholar
[12] Nechaev S K, Semenov A N, Koleva M K 1987 Physica A: Statist. Mech. Appl. 140 506
Google Scholar
[13] Chen W, Li Y, Zhao H, Liu L, Chen J, An L 2015 Polymer 64 93
Google Scholar
[14] Cao J, Likhtman A E 2015 ACS Macro. Lett. 4 1376
Google Scholar
[15] Luo C, Kröger M, Sommer J U 2017 Polymer 109 71
Google Scholar
[16] Kremer K, Grest G S 1990 J. Chem. Phys. 92 5057
Google Scholar
[17] Wang Z, Likhtman A E, Larson R G 2012 Macromolecules 45 3557
Google Scholar
[18] McLeish T C B 2002 Adv. Phys. 51 1379
Google Scholar
[19] Cao J, Likhtman A E 2012 Phy. Rev. Lett. 108 028302
Google Scholar
[20] DoiY, Matsubara K, Ohta Y, Nakano T, Kawaguchi D, Takahashi Y, Takano A, Matsushita Y 2015 Macromolecules 48 3140
Google Scholar
[21] Boukany P E, Wang S Q, Wang X 2009 J. Rheol. 53 617
Google Scholar
[22] Jeong S, Kim J M, Baig C 2017 Macromolecules 50 3424
Google Scholar
下载:
计量
- 文章访问数: 7425
- PDF下载量: 97
- 被引次数: 0
