-
合金铸锭凝固过程中经常伴随着游离枝晶在运动的同时生长运动及相互碰撞等现象, 其对铸锭的温度场、流场、溶质场及微观组织等具有不可忽视的影响, 是研究铸锭凝固组织形成的关键问题之一. 元胞自动机-格子玻尔兹曼(CA-LB)耦合模型近年来在处理运动枝晶方面发展迅速, 该模型不仅可以很好地维持运动枝晶的形貌, 还可以合理地计算出枝晶间的相互碰撞. 本文改进了模拟游离枝晶运动生长的元胞自动机-格子玻尔兹曼模型, 采用交替方向隐式迭代法求解导热微分方程, 模拟参数不受稳定性条件限制. 分别验证了流场与固相和温度场耦合的准确性. 随后采用该模型分别模拟了Fe-0.34%C合金铸锭中等轴晶运动与否的凝固过程, 模拟结果表明, 等轴晶的运动会增大与临近枝晶的接触概率, 会使铸锭中的晶粒尺寸更加均匀; 枝晶的运动还会改变熔体中心部位的溶质分布, 特别是增大了顶部正偏析的大小以及范围; 等轴晶的运动会受到柱状晶的阻碍, 所以CET区域受枝晶运动的影响不大.The solidification process of alloy ingot is often accompanied by the phenomena of free dendrites growing and colliding with each other while moving, which has a non-negligible influence on the temperature field, flow field, solute field and microstructure of the ingot, and it is one of the key issues in the study of ingot solidification organization formation. The cellular automata-lattice Boltzmann (CA-LB) coupling model has been developed rapidly in recent years in dealing with the moving dendrites, which can not only maintain the morphology of the moving dendrites well, but also calculate the mutual collisions between the dendrites reasonably. In this work, the cell-automata-lattice Boltzmann model for simulating the growth of free dendrites is improved. Alternating direction implicit iteration method is used to solve the differential heat conduction equation, and the simulation parameters are not limited by stability conditions in this method. In this research, the accuracy of the flow-solid coupling of the model is verified by taking the flow around a circular cylinder for example, and the temperature field of the model is well coupled under the natural convection condition. Finally, the solidification process of Fe-0.34%C alloy ingots with or without equiaxed grain movement is simulated using this model. The simulation results show that the movement of equiaxed grains increases the contact probability with the neighboring dendrites, which leads to a more uniform grain size in the ingot; the movement of dendrites also changes the solute distribution in the center of the melt, especially increasing the size and range of the hot-top segregation; the movement of equiaxed grains is impeded by the columnar crystals, and therefore the CET region is not much affected by the movement of dendrites.
-
Keywords:
- ingot /
- macroscopic segregation /
- numerical simulation /
- dendrite movement
[1] Qi X B, Chen Y, Kang X H, Li D Z, Gong T Z 2017 Sci Rep 7 45770
 Google Scholar
Google Scholar
[2] Rátkai L, Pusztai T, Gránásy L 2019 npj Comput. Mater. 5 113
 Google Scholar
Google Scholar
[3] 张士杰, 王颖明, 王琦, 李晨宇, 李日 2021 70 238101
 Google Scholar
Google Scholar
Zhang S J, Wang Y M, Wang Q, Li C Y, Li R 2021 Acta Phys. Sin. 70 238101
 Google Scholar
Google Scholar
[4] Sakane S, Takaki T, Ohno M, Shibuta Y, Aoki T 2020 Comput. Mater. Sci. 178 109639
 Google Scholar
Google Scholar
[5] Ren J K, Chen Y, Cao Y F, Sun M Y, Xu B, Li D Z 2020 J. Mater. Sci. Tech. 58 171
 Google Scholar
Google Scholar
[6] Yamanaka N, Sakane S, Takaki T 2021 Comput. Mater. Sci. 197 110658
 Google Scholar
Google Scholar
[7] Zhang S J, Zhu B F, Li Y B, Zhang Y, Li R 2024 Comput. Mater. Sci. 245 113308
 Google Scholar
Google Scholar
[8] Liu L, Pian S, Zhang Z, Bao Y C, Li R, Chen H J 2018 Comput. Mater. Sci. 146 9
 Google Scholar
Google Scholar
[9] Wang Q, Wang Y M, Zhang S J, Guo B X, Li C Y, Li R 2021 Crystals 11 1056
 Google Scholar
Google Scholar
[10] Sakane S, Aoki T, Takaki T 2022 Comput. Mater. Sci. 211 111542
 Google Scholar
Google Scholar
[11] Meng S X, Zhang A, Guo Z P, Wang Q G 2020 Comput. Mater. Sci. 184 109784
 Google Scholar
Google Scholar
[12] Takaki T 2023 IOP Conf. Ser. Mater. Sci. Eng. 1274 012009
 Google Scholar
Google Scholar
[13] Flemings M C, Mehrabian R, Nereo G E 1968 T. Metall. Soc. AIME 239 1449
[14] Bennon W D, Incropera F P 1987 Int. J. Heat Mass Tran. 30 2161
 Google Scholar
Google Scholar
[15] Bennon W D, Incropera F P 1987 Int. J. Heat Mass Tran. 30 2171
 Google Scholar
Google Scholar
[16] Beckermann C, Viskanta R 1988 Physicochemical Hydrodynamics 10 195
[17] Gu J P, Beckermann C 1999 Metall. Mater. Trans. A 30 1357
 Google Scholar
Google Scholar
[18] Wu M, Ludwig A, Kharicha A 2016 Appl. Math. Model. 41 102
 Google Scholar
Google Scholar
[19] Zhang Z, Bao Y, Liu L, Pian S, Li R 2018 Metall. Mater. Trans. A 49 2750
 Google Scholar
Google Scholar
[20] Zhang S, Li Y, Zhang S, Zhu B, Li R 2025 Int. J. Therm. Sci. 211 109737
 Google Scholar
Google Scholar
[21] Rappaz M, Thévoz P H 1987 Acta Metall. 35 2929
 Google Scholar
Google Scholar
[22] Zhu M F, Lee S Y, Hong C P 2004 Phys. Rev. E 69 061610
 Google Scholar
Google Scholar
[23] Sun D K, Zhu M F, Pan S Y, Yang C R, Raabe D 2011 Comput. Math. Appl. 61 3585
 Google Scholar
Google Scholar
[24] Zhu M, Stefanescu D 2007 Acta Mater. 55 1741
 Google Scholar
Google Scholar
[25] Wen B, Zhang C, Tu Y, Wang C, Fang H 2014 J. Comput. Phys. 266 161
 Google Scholar
Google Scholar
[26] Mei R, Yu D, Shyy W, Luo L S 2002 Phys. Rev. E 65 041203
 Google Scholar
Google Scholar
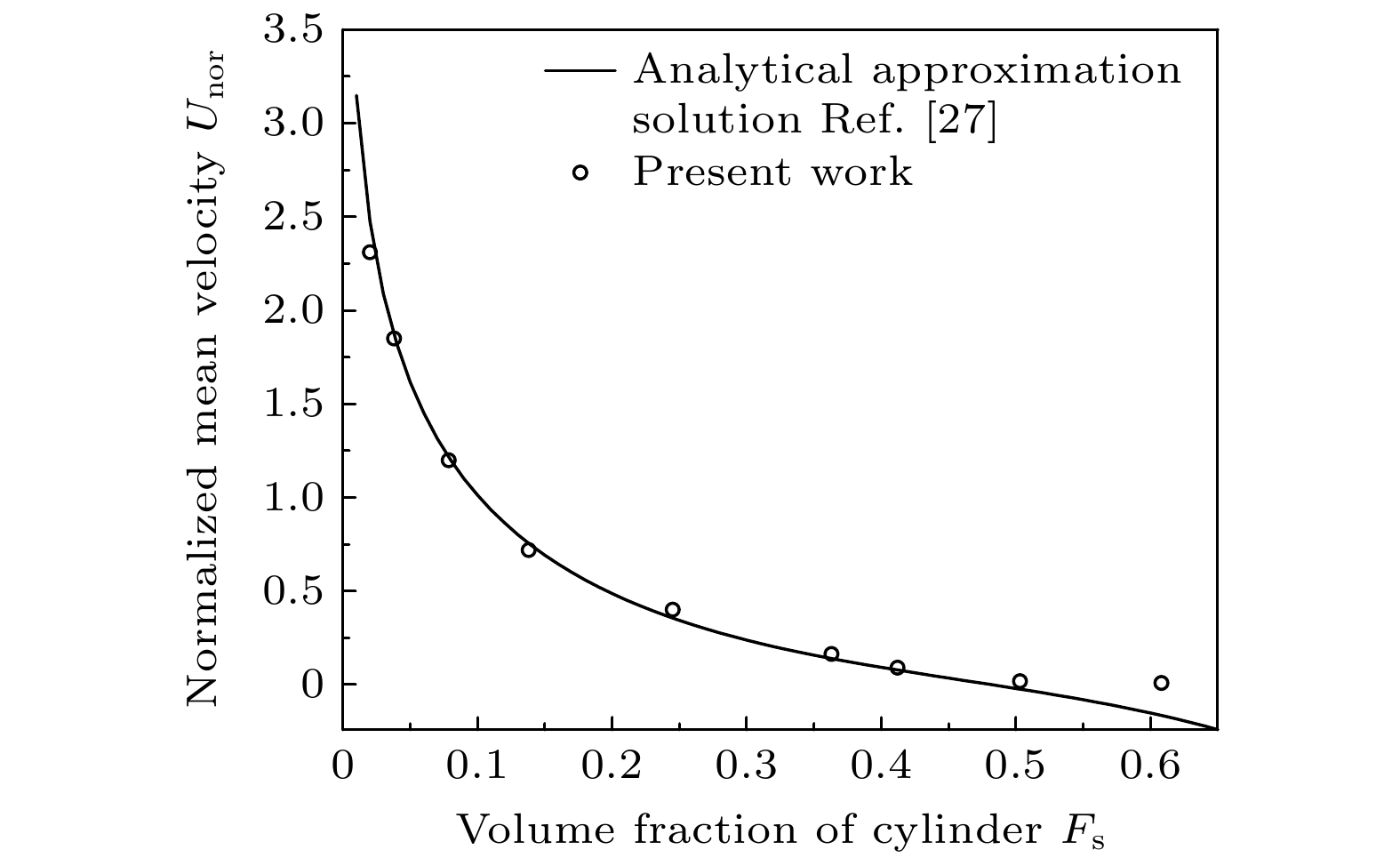
[27] Drummond J E, Tahir M I 1984 Int. J. Multiphase Flow 10 515
 Google Scholar
Google Scholar
[28] 张照 2020 硕士学位论文 (天津: 河北工业大学)
Zhang Z 2020 M. S. Thesis (Tianjin: Hebei University of Technology
[29] Shan X 1997 Phys. Rev. E 55 2780
 Google Scholar
Google Scholar
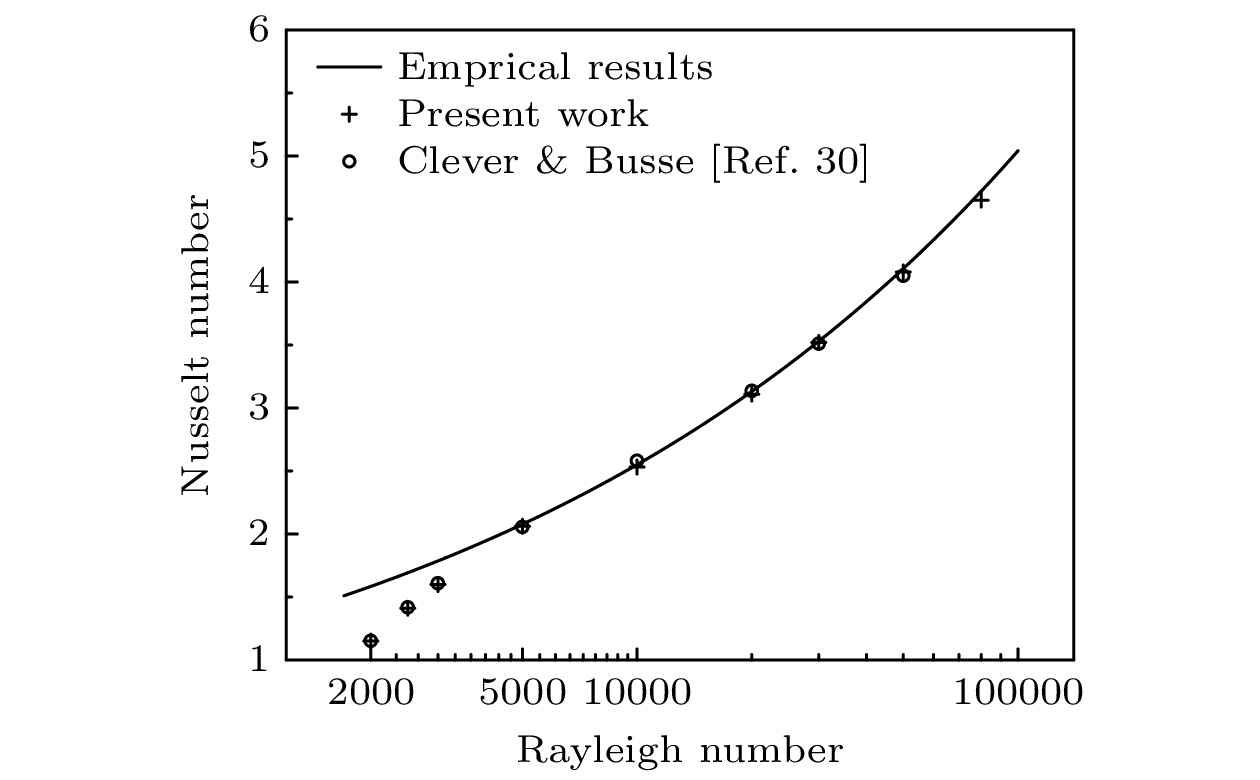
[30] Clever R M, Busse F H 1974 J. Fluid Mech. 65 625
 Google Scholar
Google Scholar
[31] Wu M, Könözsy L, Ludwig A, Schützenhöfer W, Tanzer R 2008 Steel Res. Int. 79 637
 Google Scholar
Google Scholar
[32] Luo S, Wang W, Zhu M 2018 Int. J. Heat Mass Tran. 116 940
 Google Scholar
Google Scholar
[33] Ge H H, Li J, Guo Q T, Ren F L, Xia M X, Yao J H, Li J G 2021 Metall. Mater. Trans. B 52 2992
 Google Scholar
Google Scholar
-
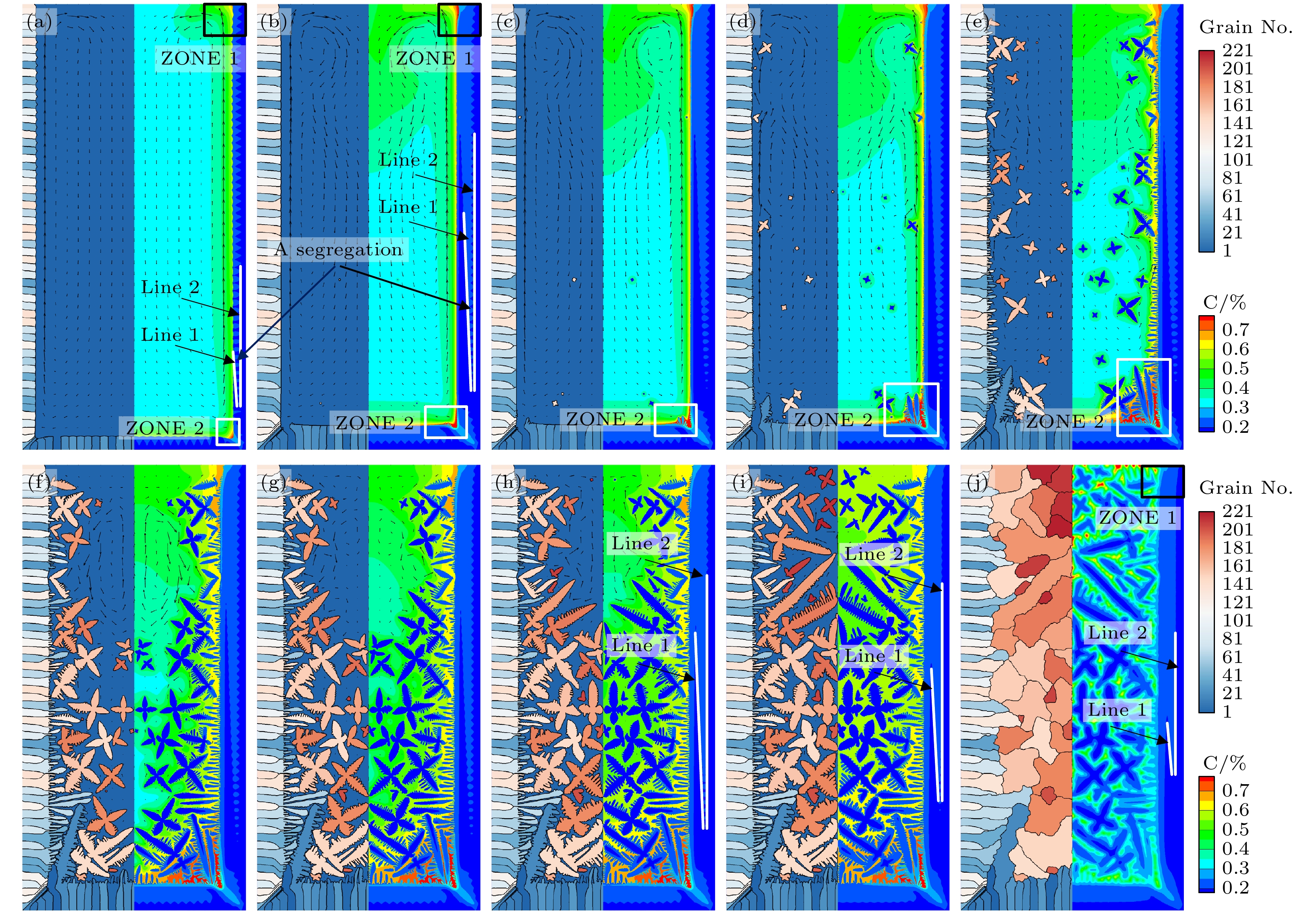
图 8 不考虑等轴晶运动时铸锭的凝固过程 (a) t = 2.0 s; (b) t = 4.5 s; (c) t = 4.6 s; (d) t = 4.8 s; (e) t = 5.2 s; (f) t = 5.6 s; (g) t = 6.0 s; (h) t = 7.0 s; (i) t = 10.0 s; (j) t = 18.0 s
Fig. 8. Solidification process of ingot without considering the equiaxial crystal motion: (a) t = 2.0 s; (b) t = 4.5 s; (c) t = 4.6 s; (d) t = 4.8 s; (e) t = 5.2 s; (f) t = 5.6 s; (g) t = 6.0 s; (h) t = 7.0 s; (i) t = 10.0 s; (j) t = 18.0 s.
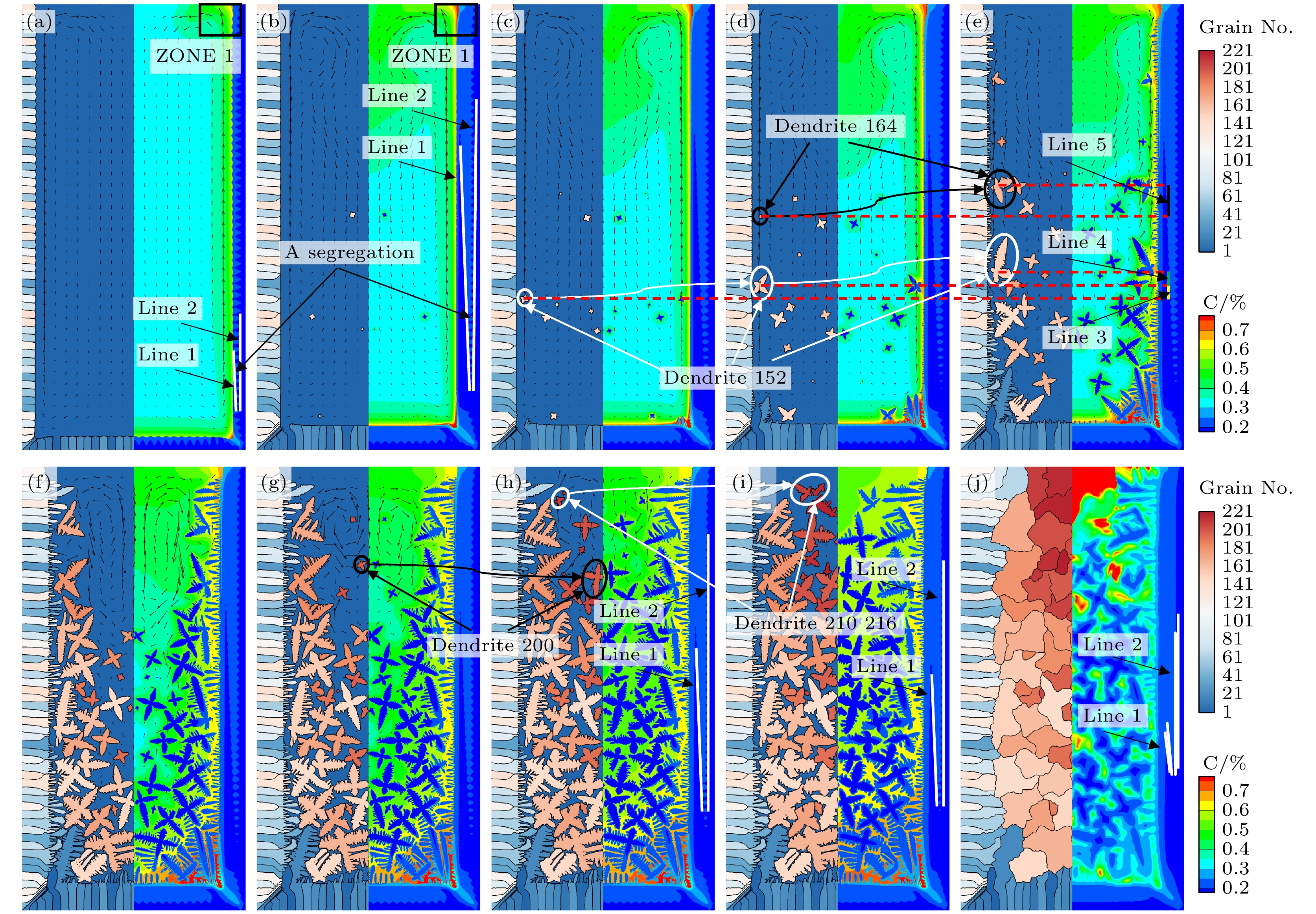
图 9 考虑等轴晶运动的铸锭凝固过程 (a) t = 2.0 s; (b) t = 4.5 s; (c) t = 4.6 s; (d) t = 4.8 s; (e) t = 5.2 s; (f) t = 5.6 s; (g) t = 6.0 s; (h) t = 7.0 s; (i) t = 10.0 s; (j) t = 18.0 s
Fig. 9. Solidification process of ingot considering equiaxial crystal motion: (a) t = 2.0 s; (b) t = 4.5 s; (c) t = 4.6 s; (d) t = 4.8 s; (e) t = 5.2 s; (f) t = 5.6 s; (g) t = 6.0 s; (h) t = 7.0 s; (i) t = 10.0 s; (j) t = 18.0 s.
表 1 不同位置的${C_{\text{e}}}$与${D_{\text{e}}}$的取值方法
Table 1. Methods of taking values of ${C_{\text{e}}}$ and ${D_{\text{e}}}$ at different locations.
液相 固相 界面 界面与固相之间 界面与液相之间 ${C_{\text{e}}}$ ${C_{\text{l}}}$ ${C_{\text{s}}}/k$ ${C_{\text{l}}}$ ${C_{\text{l}}}$ ${C_{\text{l}}}$ ${D_{\text{e}}}$ ${D_{\text{l}}}$ ${D_{\text{s}}}$ ${D_{\text{l}}}$ ${D_{\text{s}}}$ ${D_{\text{l}}}$ 表 2 模拟用到的参数
Table 2. Parameters used for simulation.
Physical parameter Value Solidus temperature, ${T_{\text{m}}}/K$ 1811.15 Liquidus temperature, ${T_0}/K$ 1723.15 Liquidus slope, ${m_{\text{l}}}/({{\mathrm{K}} {\cdot} {{\text{%}} ^{-1}}})$ –80.45 Interface kinetics coefficient, ${\mu _{\text{k}}}/({1{0^{ - 3}}\;{\mathrm{m}} {\cdot} {{\mathrm{s}}^{ - 1}} {\cdot} {\mathrm{K}}})$ 2 Kinetic anisotropy strength, ${\delta _{\text{k}}}$ 0.3 Thermodynamic anisotropy, ${\delta _{\text{t}}}$ 0.3 Liquid Viscosity, $\nu /({1{0^{ - 3}}\;{\mathrm{kg}} {\cdot} {{\mathrm{m}}^{ - 1}} {\cdot} {{\mathrm{s}}^{ - 1}}})$ 3.6 Diffusivity in liquid, ${D_{\text{l}}}/( {{{10}^{ - 8}}\;{{\text{m}}^2} {\cdot} {{\text{s}}^{ - 1}}} )$ 2 Diffusivity in solid, ${D_{\text{s}}}/( {{{10}^{ - 9}}\;{{\text{m}}^2} {\cdot} {{\text{s}}^{ - 1}}} )$ 1 Partition coefficient, $k$ 0.36 Average Gibbs-Tomson
coefficient, $ {\bar \varGamma /( {{{10}^{ - 7}}\;{\text{m}} {\cdot} {\text{K}}} )}$1.9 Specific heat capacity, ${C_{\text{p}}}/( {{\text{J}} {\cdot} {\text{k}}{{\text{g}}^{ - 1}} {\cdot} {{\text{K}}^{ - 1}}} )$ 455 Convective heat transfer
coefficient, $h/({\mathrm{W}} {\cdot} {{\mathrm{m}}^{ - 2}} {\cdot} {{\mathrm{K}}^{ - 1}})$600 Thermal conductivity, $\lambda /({\text{W}} {\cdot} {{\text{m}}^{ - 1}} {\cdot} {{\text{K}}^{ - 1}})$ 30 Thermal expansion coefficient, $ {\beta _{\text{T}}}/( {{{10}^{ - 4}}\;{{\mathrm{K}}^{ - 1}}} ) $ 2 Solutal expansion coefficient, $ {\beta _{\text{c}}}/( {{{10}^{ - 2}} \;{{\text{%}} ^{ - 1}}} ) $ 1.1 Latent heat, $L/( {{{10}^3}\;{\text{J}} {\cdot} {\text{k}}{{\text{g}}^{ - 1}}} )$ 269.55 Density, $\rho /( {{\text{kg}} {\cdot} {{\text{m}}^{ - 3}}} )$ 7001 表 3 不同位置的平均浓度以及偏析程度
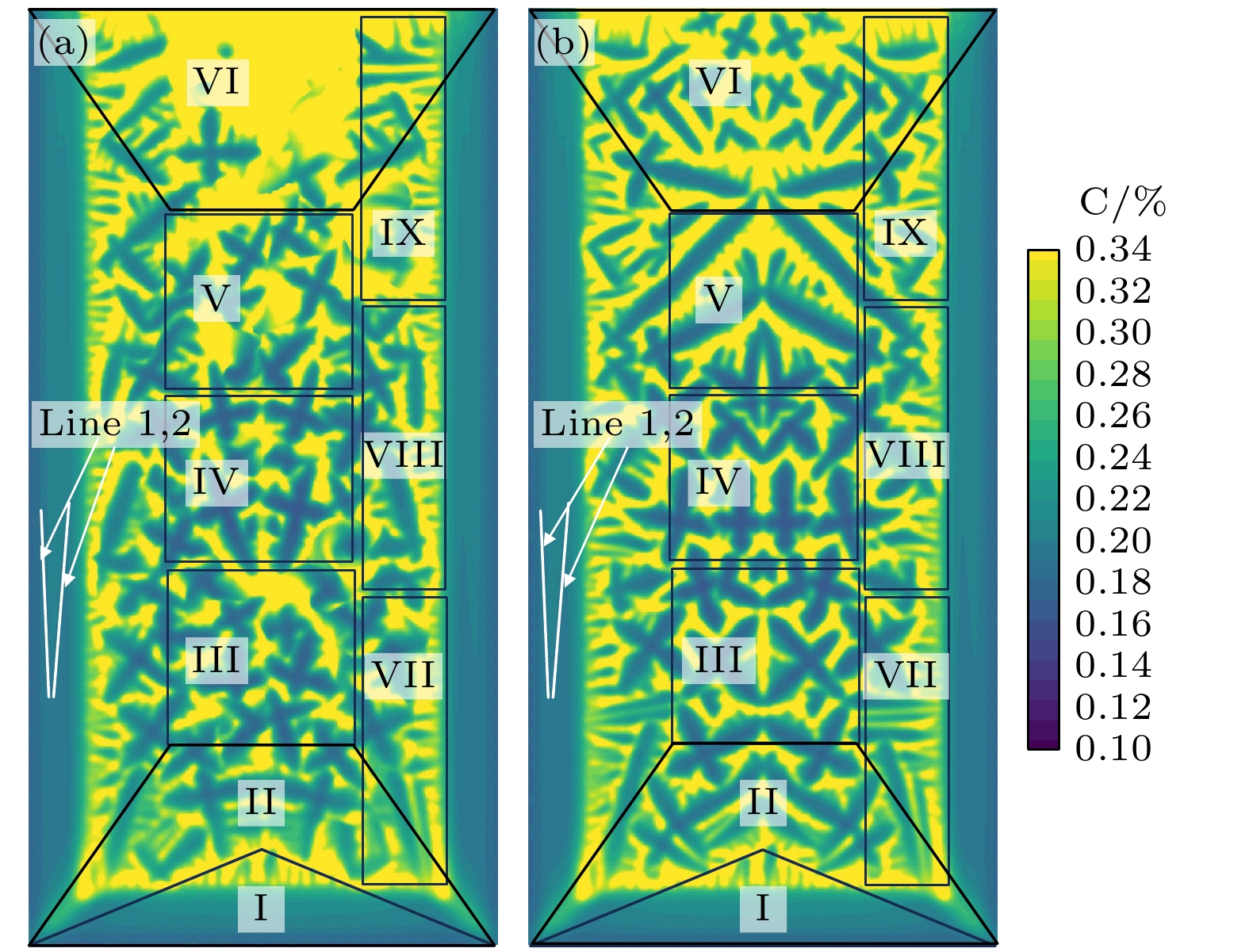
Table 3. Average concentration and segregation of index (SI) at different locations.
Ⅰ Ⅱ Ⅲ Ⅳ Ⅴ Ⅵ Ⅶ Ⅷ Ⅸ 运动 0.227 0.257 0.292 0.309 0.323 0.441 0.282 0.289 0.351 偏析/% –33.2 –24.4 –14.1 –9.1 –5.0 29.7 –17.1 –15.0 3.2% 不运动 0.228 0.278 0.298 0.3 0.341 0.384 0.278 0.289 0.345 偏析/% –32.9 –18.2 –12.4 –11.8 0.3 12.9 –18.2 –15.0 1.5% -
[1] Qi X B, Chen Y, Kang X H, Li D Z, Gong T Z 2017 Sci Rep 7 45770
 Google Scholar
Google Scholar
[2] Rátkai L, Pusztai T, Gránásy L 2019 npj Comput. Mater. 5 113
 Google Scholar
Google Scholar
[3] 张士杰, 王颖明, 王琦, 李晨宇, 李日 2021 70 238101
 Google Scholar
Google Scholar
Zhang S J, Wang Y M, Wang Q, Li C Y, Li R 2021 Acta Phys. Sin. 70 238101
 Google Scholar
Google Scholar
[4] Sakane S, Takaki T, Ohno M, Shibuta Y, Aoki T 2020 Comput. Mater. Sci. 178 109639
 Google Scholar
Google Scholar
[5] Ren J K, Chen Y, Cao Y F, Sun M Y, Xu B, Li D Z 2020 J. Mater. Sci. Tech. 58 171
 Google Scholar
Google Scholar
[6] Yamanaka N, Sakane S, Takaki T 2021 Comput. Mater. Sci. 197 110658
 Google Scholar
Google Scholar
[7] Zhang S J, Zhu B F, Li Y B, Zhang Y, Li R 2024 Comput. Mater. Sci. 245 113308
 Google Scholar
Google Scholar
[8] Liu L, Pian S, Zhang Z, Bao Y C, Li R, Chen H J 2018 Comput. Mater. Sci. 146 9
 Google Scholar
Google Scholar
[9] Wang Q, Wang Y M, Zhang S J, Guo B X, Li C Y, Li R 2021 Crystals 11 1056
 Google Scholar
Google Scholar
[10] Sakane S, Aoki T, Takaki T 2022 Comput. Mater. Sci. 211 111542
 Google Scholar
Google Scholar
[11] Meng S X, Zhang A, Guo Z P, Wang Q G 2020 Comput. Mater. Sci. 184 109784
 Google Scholar
Google Scholar
[12] Takaki T 2023 IOP Conf. Ser. Mater. Sci. Eng. 1274 012009
 Google Scholar
Google Scholar
[13] Flemings M C, Mehrabian R, Nereo G E 1968 T. Metall. Soc. AIME 239 1449
[14] Bennon W D, Incropera F P 1987 Int. J. Heat Mass Tran. 30 2161
 Google Scholar
Google Scholar
[15] Bennon W D, Incropera F P 1987 Int. J. Heat Mass Tran. 30 2171
 Google Scholar
Google Scholar
[16] Beckermann C, Viskanta R 1988 Physicochemical Hydrodynamics 10 195
[17] Gu J P, Beckermann C 1999 Metall. Mater. Trans. A 30 1357
 Google Scholar
Google Scholar
[18] Wu M, Ludwig A, Kharicha A 2016 Appl. Math. Model. 41 102
 Google Scholar
Google Scholar
[19] Zhang Z, Bao Y, Liu L, Pian S, Li R 2018 Metall. Mater. Trans. A 49 2750
 Google Scholar
Google Scholar
[20] Zhang S, Li Y, Zhang S, Zhu B, Li R 2025 Int. J. Therm. Sci. 211 109737
 Google Scholar
Google Scholar
[21] Rappaz M, Thévoz P H 1987 Acta Metall. 35 2929
 Google Scholar
Google Scholar
[22] Zhu M F, Lee S Y, Hong C P 2004 Phys. Rev. E 69 061610
 Google Scholar
Google Scholar
[23] Sun D K, Zhu M F, Pan S Y, Yang C R, Raabe D 2011 Comput. Math. Appl. 61 3585
 Google Scholar
Google Scholar
[24] Zhu M, Stefanescu D 2007 Acta Mater. 55 1741
 Google Scholar
Google Scholar
[25] Wen B, Zhang C, Tu Y, Wang C, Fang H 2014 J. Comput. Phys. 266 161
 Google Scholar
Google Scholar
[26] Mei R, Yu D, Shyy W, Luo L S 2002 Phys. Rev. E 65 041203
 Google Scholar
Google Scholar
[27] Drummond J E, Tahir M I 1984 Int. J. Multiphase Flow 10 515
 Google Scholar
Google Scholar
[28] 张照 2020 硕士学位论文 (天津: 河北工业大学)
Zhang Z 2020 M. S. Thesis (Tianjin: Hebei University of Technology
[29] Shan X 1997 Phys. Rev. E 55 2780
 Google Scholar
Google Scholar
[30] Clever R M, Busse F H 1974 J. Fluid Mech. 65 625
 Google Scholar
Google Scholar
[31] Wu M, Könözsy L, Ludwig A, Schützenhöfer W, Tanzer R 2008 Steel Res. Int. 79 637
 Google Scholar
Google Scholar
[32] Luo S, Wang W, Zhu M 2018 Int. J. Heat Mass Tran. 116 940
 Google Scholar
Google Scholar
[33] Ge H H, Li J, Guo Q T, Ren F L, Xia M X, Yao J H, Li J G 2021 Metall. Mater. Trans. B 52 2992
 Google Scholar
Google Scholar
计量
- 文章访问数: 866
- PDF下载量: 19
- 被引次数: 0













 下载:
下载: