-
基于BOUT++代码研究了托卡马克高约束模等离子体中低杂波(LHW)注入对边缘台基区剥离气球模(P-B模)线性和非线性特性的影响. 模拟中分别考虑了LHW驱动的常规主等离子体电流和刮削层螺旋电流丝(HCF)产生三维扰动磁场对P-B模的作用. 线性结果表明, LHW驱动的主等离子体电流通过降低平衡的归一化压强梯度和磁剪切, 使得线性环向模谱整体向高模数和低增长率的方向移动. 非线性模拟表明, 由于线性模谱的展宽, LHW驱动的主等离子体电流对P-B模不同模式具有整体的抑制效果, 可以降低边缘局域模(ELM)造成的台基能量损失; LHW驱动HCF产生的三维扰动磁场可以通过增强不同模式之间的耦合, 促进主模之外的其他模式增长来降低ELM造成的能量损失. 研究发现, HCF产生的三维扰动磁场促进增长的P-B模式集中在较高模数, 当P-B模的主导模式远离此模数区间, ELM能量损失降低更明显. 研究结果有助于深入理解LHW控制ELM实验中的物理机制.The high-confinement mode (H-mode) significantly enhances the energy and particle confinement in fusion plasma compared with the low-confinement mode (L-mode), and it is the basic operation scenario for ITER and CFETR. Edge localized mode (ELM) often appears in H-mode, helping to expel impurities to maintain a longer stable state. However, the particle burst and energy burst from ELM eruptions can severely damage the first wall of fusion device, so, it is necessary to control the ELM. Experiments on EAST tokamak and HL-2A tokamak have been conducted with ELM mitigation by lower hybrid wave (LHW), confirming the effect of LHW on ELMs, but the physical mechanism of ELM mitigation by LHW is still not fully understood. In this paper, the influences of LHW injection on the linear and nonlinear characteristics of peeling-ballooning mode (P-B mode) are investigated in the edge pedestal region of H-mode plasma in tokamak by using the BOUT++ code. The simulations take into consideration both the conventional main plasma current driven by LHW and the three-dimensional perturbed magnetic field generated by the scrape-off layer helical current filament (HCF) on the P-B mode. The linear results show that the core plasma current driven by LHW moves the linear toroidal mode spectrum towards higher mode numbers and lower growth rates by reducing the normalized pressure gradient and magnetic shear of the equilibrium. Nonlinear simulations indicate that due to the broadening of the linear mode spectrum, the core current driven by LHW can reduce the pedestal energy loss caused by ELM through globally suppressing different toroidal modes of the P-B mode, and the three-dimensional perturbed magnetic field generated by LHW-driven HCF can reduce the energy loss caused by ELMs through promoting the growth of modes other than the main mode and enhancing the coupling between different modes. It is found in the study that the P-B mode promoted by the three-dimensional perturbed magnetic field generated by HCF has a mode number threshold, and when the dominant mode of the P-B mode is far from the mode number threshold driven by the three-dimensional perturbed magnetic field, the energy loss due to ELMs is more significantly reduced. These results contribute to a more in-depth understanding of the physical mechanism in ELM control experiment by LHW.
-
Keywords:
- magnetic confinement fusion plasma /
- edge localized modes /
- lower hybrid wave /
- peeling-ballooning modes
[1] Zohm H 1996 Plasma Phys. Control. Fusion 38 105
Google Scholar
[2] Leonard A W 2014 Phys. Plasmas 21 090501
Google Scholar
[3] Loarte A, Saibene G, Sartori R, et al. 2003 Plasma Phys. Control. Fusion 45 1549
Google Scholar
[4] Lang P T, Loarte A, Saibene G, et al. 2013 Nucl. Fusion 53 043004
Google Scholar
[5] Loarte A, Huijsmans G, Futatani S, et al. 2014 Nucl. Fusion 54 033007
Google Scholar
[6] Hughes J W, Hubbard A E, Wallace G, et al. 2010 Nucl. Fusion 50 064001
Google Scholar
[7] Wan B, Li J, Guo H, Liang Y, Xu G, Gong X Z for the EAST Team, International Collaborators 2013 Nucl. Fusion 53 104006
Google Scholar
[8] Rossel J X, Moret J M, Coda S, Sauter O, Goodman T P, Felici F, Testa D, Martin Y 2012 Nucl. Fusion 52 032004
Google Scholar
[9] Felici F, Rossel J X, Duval B P, Coda S, Goodman T P, Martin Y, Moret J M, Sauter O, the TCV Team 2013 Nucl. Fusion 53 113018
Google Scholar
[10] Baylor L R, Commaux N, Jernigan T C, et al. 2013 Phys. Rev. Lett. 110 245001
Google Scholar
[11] Chen S Y, Huang J, Sun T T, Wang Z H, Tang C J 2014 Phys. Plasmas 21 112512
Google Scholar
[12] Evans T E, Moyer R A, Watkins J G, et al. 2005 J. Nucl. Mater. 337–339 691
Google Scholar
[13] Canik J M, Maingi R, Evans T E, et al. 2010 Nucl. Fusion 50 034012
Google Scholar
[14] Xiao W W, Diamond P H, Zou X L, et al. 2012 Nucl. Fusion 52 114027
Google Scholar
[15] Huang J, Chen S Y, Wang Z H, Tang C J 2015 Phys. Plasmas 22 122507
Google Scholar
[16] Degeling A W, Martin Y R, Lister J B, Villard L, Dokouka V N, Lukash V E, Khayrutdinov R R 2003 Plasma Phys. Control. Fusion 45 1637
Google Scholar
[17] Wu N, Chen S Y, Song X M, Mou M L, Huang J, Wang Z T, Tang C J, Song X, Xia F, Jiang M, HL-2A Team 2017 Phys. Plasmas 24 092507
Google Scholar
[18] Zhang H M, Wu J, Li J X, Yao L M, Xu J C, Wu Y Z, Liu Q Y, Guo P C 2021 Acta Phys. Sin. 70 235203
Google Scholar
[19] 刘冠男, 李新霞, 刘洪波, 孙爱萍 2023 72 245202
Google Scholar
Liu G N, Li X X, Liu H B, Sun A P 2023 Acta Phys. Sin. 72 245202
Google Scholar
[20] Zhou T T, Xiang N, Gan C Y, Jia G Z, Chen J L 2022 Chin. Phys. B 31 095201
Google Scholar
[21] Xu Z, Wu Z W, Zhang L, Huang Y H, Gao W, Cheng Y X, Lin X D, Gao X, Chen Y J, Li L, Jie Y X, Zang Q, Liu H Q, EAST Team 2021 Chin. Phys. B 30 075205
Google Scholar
[22] Liang Y, Gong X Z, Gan K F, et al. 2013 Phys. Rev. Lett. 110 235002
Google Scholar
[23] Xiao G L, Zhong W L, Zou X L, et al. 2017 Phys. Plasmas 24 122507
Google Scholar
[24] Cui B T, Ji X Q, Sun T F, Liang S Y, Zhang J Z, Wang A, He M Y 2021 Fusion Eng. Des. 173 112963
Google Scholar
[25] Li S H, Wang N C, Ding Y H, et al. 2022 Plasma Phys. Control. Fusion 64 075005
Google Scholar
[26] Snyder P B, Wilson H R, Ferron J R, Lao L L, Leonard A W, Osborne T H, Turnbull A D, Mossessian D, Murakami M, Xu X Q 2002 Phys. Plasmas 9 2037
Google Scholar
[27] Bernard L C, Helton F J, Moore R W 1981 Comput. Phys. Commun. 24 377
Google Scholar
[28] Pankin A Y, Bateman G, Brennan D P, Kritz A H, Kruger S, Snyder P B, Sovinec C, the NIMROD Team 2007 Plasma Phys. Control. Fusion 49 S63
Google Scholar
[29] Pamela S J P, Huijsmans G T A, Eich T, et al. 2017 Nucl. Fusion 57 076006
Google Scholar
[30] Dudson B D, Umansky M V, Xu X Q, Snyder P B, Wilson H R 2009 Comput. Phys. Commun. 180 1467
Google Scholar
[31] Xu X Q, Dudson B, Snyder P B, Umansky M V, Wilson H 2010 Phys. Rev. Lett. 105 175005
Google Scholar
[32] Xia T Y, Xu X Q 2013 Phys. Plasmas 20 052102
Google Scholar
[33] Xia T Y, Xu X Q, Xi P W 2013 Nucl. Fusion 53 073009
Google Scholar
[34] Mou M L, Huang J, Wu N, Chen S Y, Tang C J 2016 Phys. Lett. A 380 2544
Google Scholar
[35] Dong L K, Chen S Y, Mou M L, Tang C J 2020 Plasma Sci. Technol. 22 115101
Google Scholar
[36] Huang J, Chen S Y, Tang C J 2016 Phys. Plasmas 23 052513
Google Scholar
[37] Xia T Y, Gui B, Huang Y Q, Wu Y B, Xiao X T, EAST Team 2019 Nucl. Fusion 59 076043
Google Scholar
[38] Shi Y J, Xu G S, Wang F D, et al. 2011 Phys. Rev. Lett. 106 235001
Google Scholar
[39] Rice J E, Podpaly Y A, Reinke M L, et al. 2013 Nucl. Fusion 53 093015
Google Scholar
[40] Chouli B, Fenzi C, Garbet X, et al. 2014 Plasma Phys. Control. Fusion 56 095018
Google Scholar
[41] Chen W, Wang Z X 2020 Chin. Phys. Lett. 37 125001
Google Scholar
[42] Fisch N J, Rax J M 1992 Phys. Rev. Lett. 69 612
Google Scholar
[43] Smirnov A P, Harvey R W 2001 The GENRAY Ray Tracing Code CompX Report No. CompX-2000-01
[44] Ehst D A, Karney C F F 1991 Nucl. Fusion 31 1933
Google Scholar
[45] Crotinger J A, LoDestro L, Pearlstein L D, Tarditi A, Casper T A, Hooper E B 1997 CORSICA: A Comprehensive Simulation of Toroidal Magnetic-fusion Devices. Final Report to the LDRD Program (Livermore: Lawrence Livermore National Lab.) Report No: UCRL-ID-126284
[46] Xu X Q, Ma J F, Li G Q 2014 Phys. Plasmas 21 120704
Google Scholar
[47] Burrell K H 1997 Phys. Plasmas 4 1499
Google Scholar
[48] Ding B J, Bonoli P T, Tuccillo A, et al. 2018 Nucl. Fusion 58 095003
Google Scholar
[49] Li G Q, Xu X Q, Snyder P B, Turnbull A D, Xia T Y, Ma C H, Xi P W 2014 Phys. Plasmas 21 102511
Google Scholar
[50] Zhang Y, Huang J, Chen S Y, Tang C J 2017 Phys. Plasmas 24 062108
Google Scholar
[51] Li J, Guo H Y, Wan B N, et al. 2013 Nat. Phys. 9 817
Google Scholar
[52] Dong L K, Chen S Y, Mou M L, Luo Y, Qin C C, Tang C J 2023 Nucl. Fusion 63 086023
Google Scholar
[53] Liu Y, Ham C J, Kirk A, Li L, Loarte A, Ryan D A, Sun Y, Suttrop W, Yang X, Zhou L 2016 Plasma Phys. Control. Fusion 58 114005
Google Scholar
[54] Oyama N, Sakamoto Y, Isayama A, et al. 2005 Nucl. Fusion 45 871
Google Scholar
[55] Aiba N, Giroud C, Honda M, et al. 2017 Nucl. Fusion 57 126001
Google Scholar
[56] Luo Y, Chen S Y, Huang J, Xiong Y Y, Tang C J 2016 Phys. Plasmas 23 042302
Google Scholar
[57] Xi P W, Xu X Q, Wang X G, Xia T Y 2012 Phys. Plasmas 19 092503
Google Scholar
[58] 李春雨, 郝广周, 刘钺强, 王炼, 刘艺慧子 2022 71 075202
Google Scholar
Li C Y, Hao G Z, Liu Y Q, Wang L, Liu Y H Z 2022 Acta Phys. Sin. 71 075202
Google Scholar
-
图 3 不同LHW驱动电流下的(a)平行电流剖面和(b)安全因子剖面
Fig. 3. Parallel current profiles (a) and safety factor profiles (b) with different LHW-driven currents.
图 4 LHW驱动的HCF的三维结构示意图
Fig. 4. Schematic diagram of the three-dimensional structure of LHW-driven HCF.
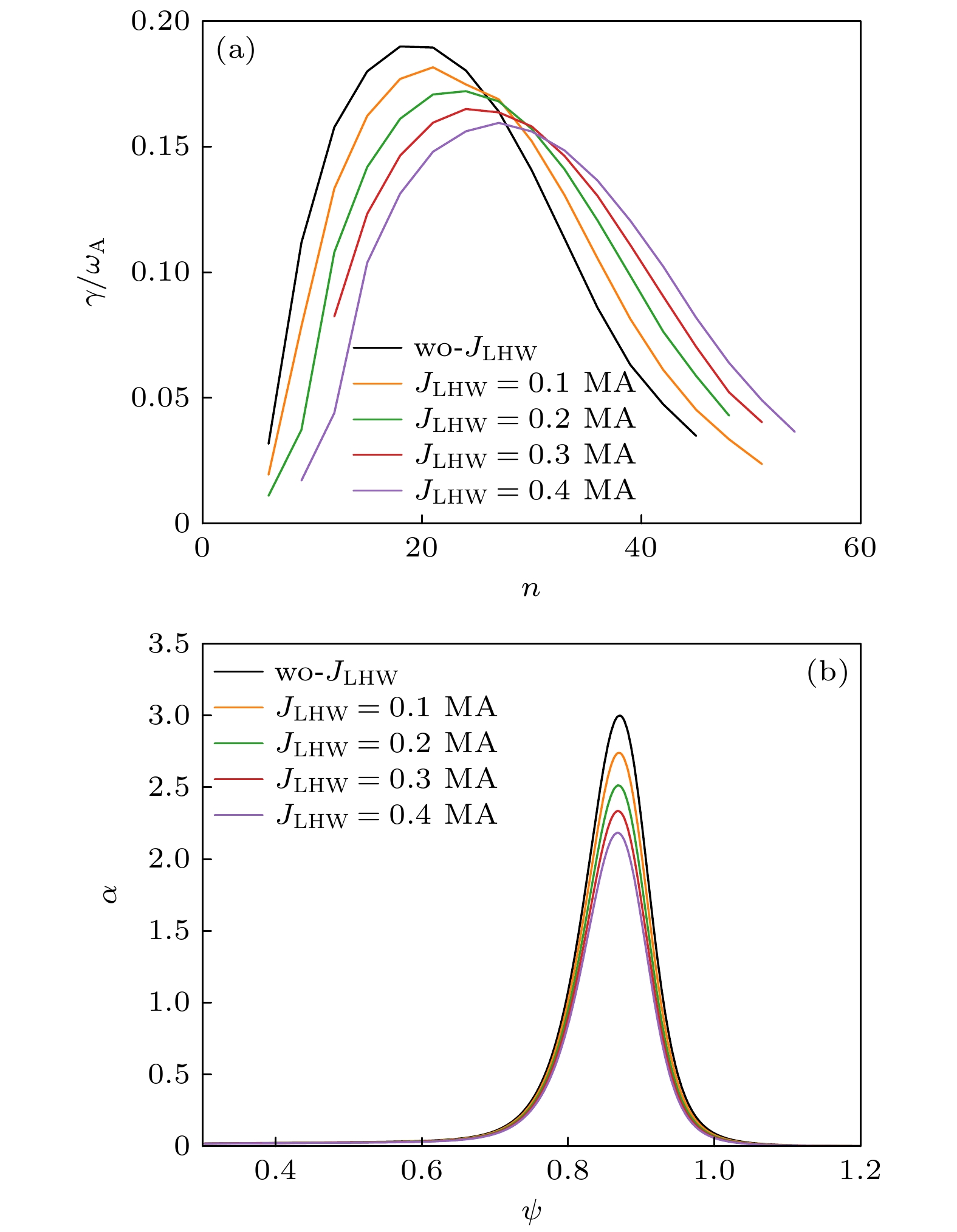
图 5 (a) P-B模归一化线性增长率, 其中$ {\omega }_{{\mathrm{A}}}=1/{\tau }_{{\mathrm{A}}} $为阿尔芬频率; (b)平衡的归一化压强梯度, 其中$ \alpha = $ $\left(2{\mu }_{0}{R}_{0}{q}^{2}{\mathrm{d}}p\right)/\left({B}^{2}{\mathrm{d}}r\right) $
Fig. 5. (a) Linear growth rates of the P-B mode; (b) normalized pressure gradient of the equilibrium with different $ {J}_{{\mathrm{L}}{\mathrm{H}}{\mathrm{W}}} $. Here, $ \alpha =\left(2{\mu }_{0}{R}_{0}{q}^{2}{\mathrm{d}}p\right)/\left({B}^{2}{\mathrm{d}}r\right) $.
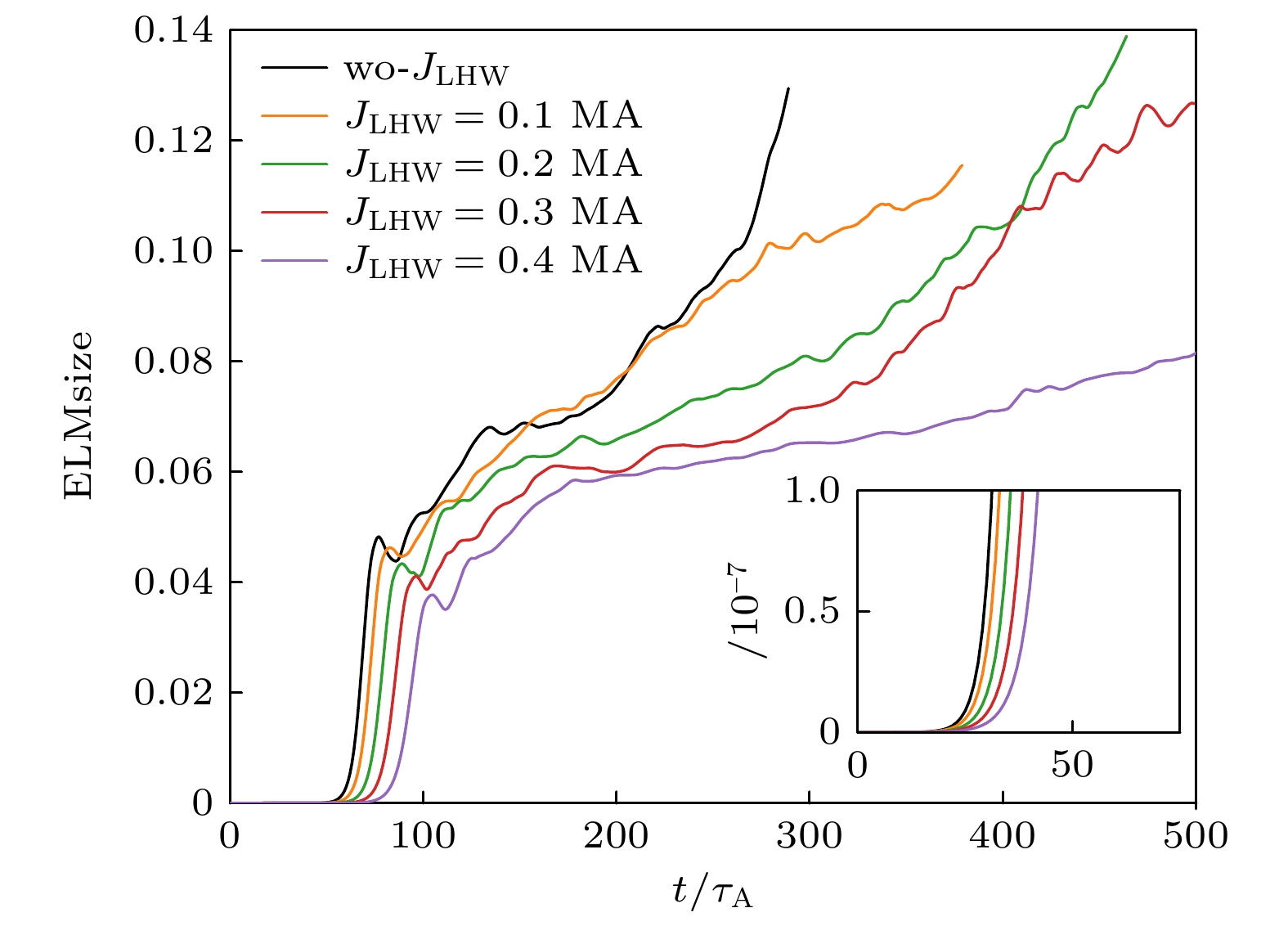
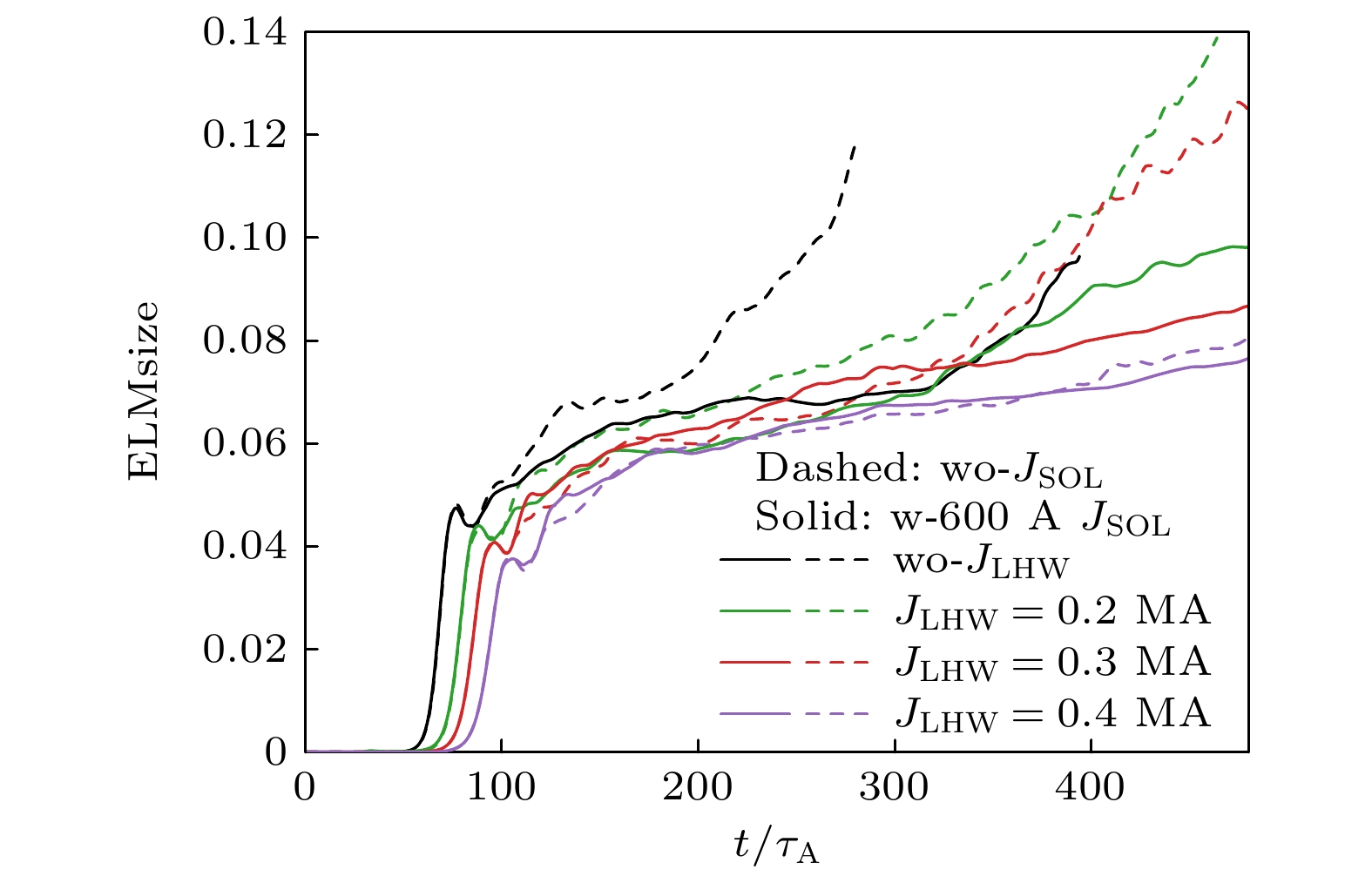
图 6 LHW驱动的不同大小$ {J}_{{\mathrm{L}}{\mathrm{H}}{\mathrm{W}}} $对ELMsize时间演化的影响, 插图为0—75$ {\tau }_{{\mathrm{A}}} $时刻的放大
Fig. 6. Influence of different $ {J}_{{\mathrm{L}}{\mathrm{H}}{\mathrm{W}}} $ driven by LHW on the time evolution of ELMsize, The inset in the lower right corner is an enlargement of the from 0 to 75$ {\tau }_{{\mathrm{A}}} $.
图 7 P-B模非线性模式演化(红色虚线为ELMsize) (a)初始平衡; (b) JLHW = 0.2 MA; (c) JLHW = 0.3 MA; (d) JLHW = 0.4 MA
Fig. 7. Temporal evolutions of the P-B mode spectrum: (a) Original equilibrium; (b) JLHW = 0.2 MA ; (c) JLHW = 0.3 MA; (d) JLHW = 0.4 MA. The red dashed line represents ELMsize.
图 8 不同大小HCF产生的$ {A}_{//{\mathrm{H}}{\mathrm{C}}{\mathrm{F}}} $对ELMsize随时间演化的影响
Fig. 8. Influence of $ {A}_{//{\mathrm{H}}{\mathrm{C}}{\mathrm{F}}} $ generated by different amplitudes of HCF on the time evolution of ELMsize.
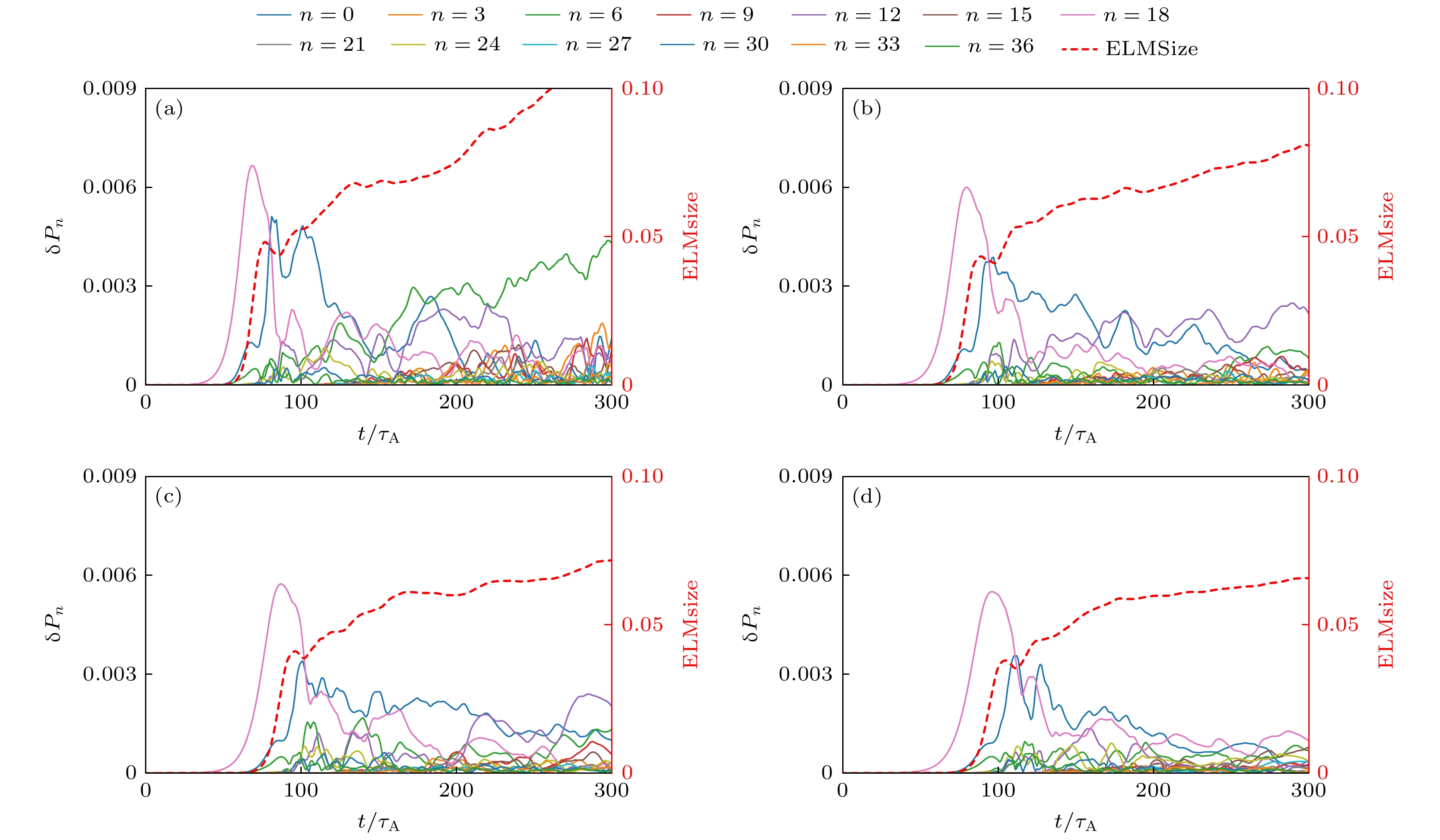
图 9 P-B模非线性模式演化, 分别对应未加入$ {A}_{//{\mathrm{H}}{\mathrm{C}}{\mathrm{F}}} $ (a), 以及300 A HCF (b), 450 A HCF (c), 600 A HCF (d) 产生的$ {A}_{//{\mathrm{H}}{\mathrm{C}}{\mathrm{F}}} $下的模拟, 图中红色虚线为ELMsize
Fig. 9. Temporal evolutions of the P-B mode spectrum, for cases without $ {A}_{//{\mathrm{H}}{\mathrm{C}}{\mathrm{F}}} $ (a) and with $ {A}_{//{\mathrm{H}}{\mathrm{C}}{\mathrm{F}}} $ generated by 300 A HCF (b), 450 A HCF (c), 600 A HCF (d). The red dashed line represents ELMsize.
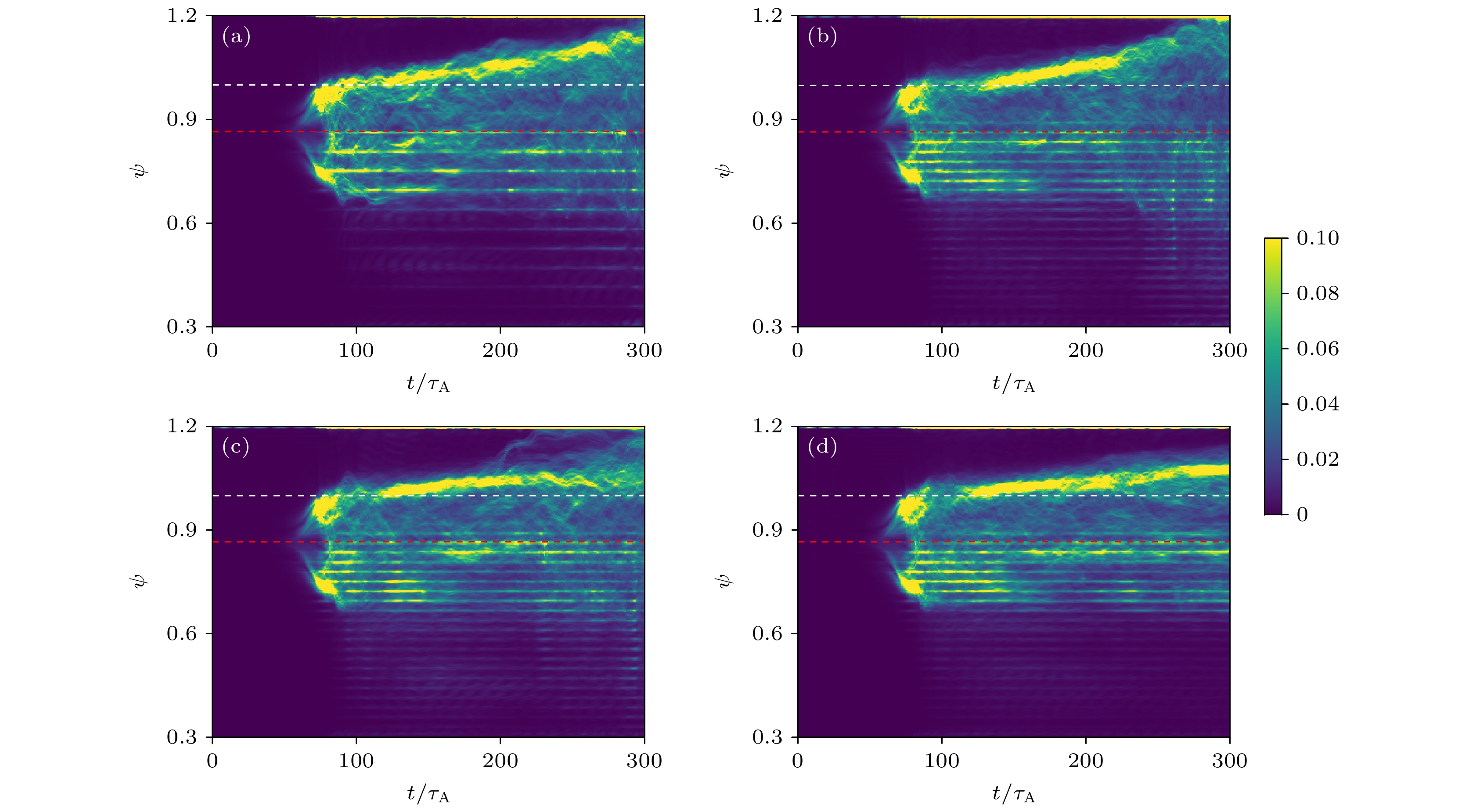
图 10 环向平均的$ E\times B $剪切流随时间的演化, 分别为未加入$ {A}_{//{\mathrm{H}}{\mathrm{C}}{\mathrm{F}}} $(a) 以及加入300 A HCF (b), 450 A HCF (c), 600 A HCF (d). 图中白色虚线为$ \psi =1 $的位置, 红色虚线为平衡压强梯度最大位置$ \psi =0.871 $
Fig. 10. Temporal evolutions of the toroidal averaged $ E\times B $ shear flow, for cases without $ {A}_{//{\mathrm{H}}{\mathrm{C}}{\mathrm{F}}} $ (a) and with $ {A}_{//{\mathrm{H}}{\mathrm{C}}{\mathrm{F}}} $ generated by 300 A HCF (b), 450 A HCF (c), 600 A HCF (d). The white and red dashed lines represent locations of $ \psi =1 $ and the maximum pressure gradient location $ \psi =0.871 $, respectively.
图 11 不同$ {J}_{{\mathrm{L}}{\mathrm{H}}{\mathrm{W}}} $电流条件下600 A HCF对ELMsize时间演化的影响
Fig. 11. Influence of 600 A HCF on the time evolution of ELMsize under different $ {J}_{{\mathrm{L}}{\mathrm{H}}{\mathrm{W}}} $ current conditions.
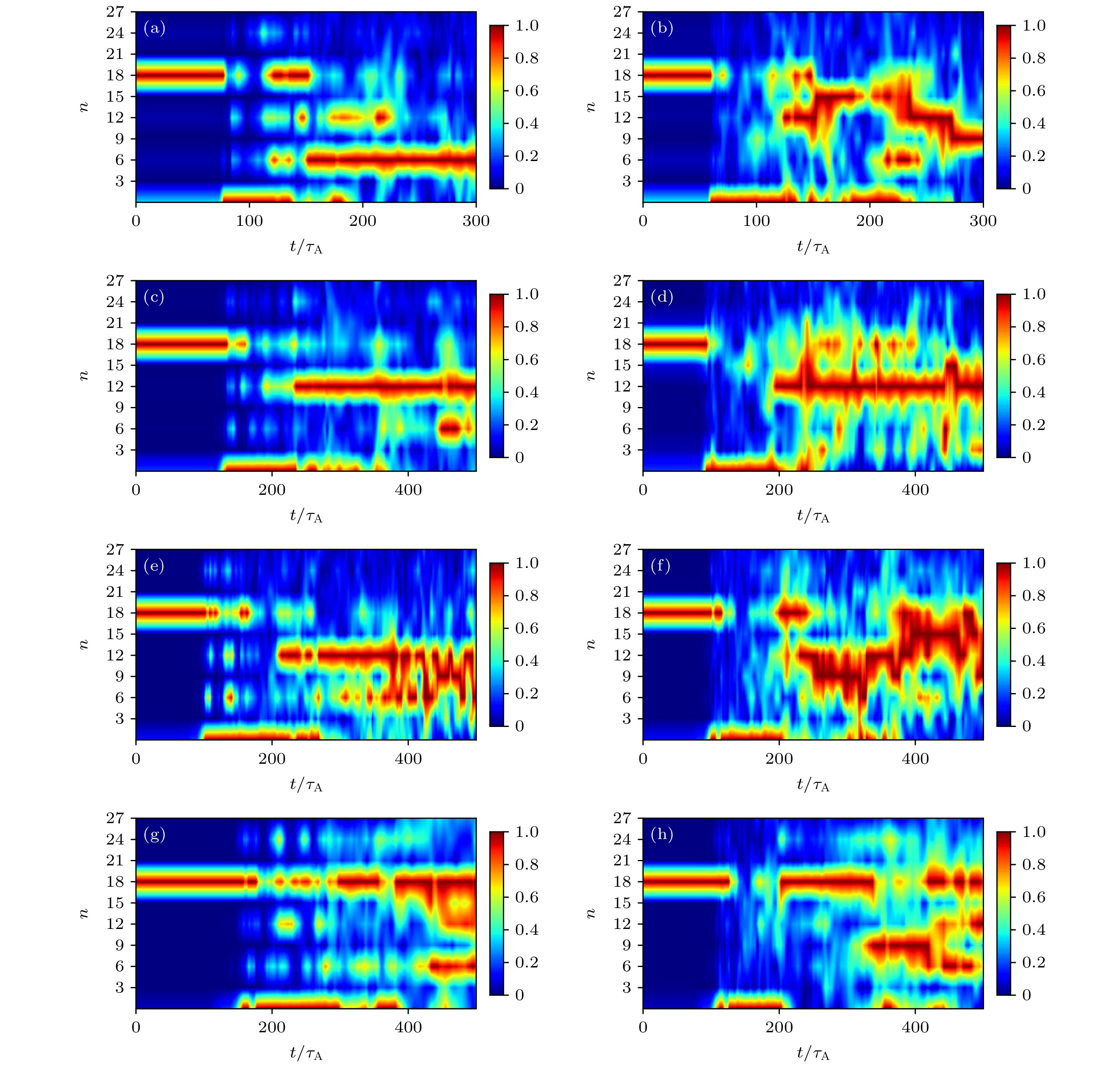
图 12 考虑HCF后的P-B模谱结构随时间的演化, 其中, 从上到下依次为初始平衡(a), (b); JLHW = 0.2 MA (c), (d); JLHW = 0.3 MA (e), (f); JLHW = 0.4 MA (g), (h)下的平衡. 左侧的一列(a), (c), (e), (g)为未加入$ {A}_{//{\mathrm{H}}{\mathrm{C}}{\mathrm{F}}} $的模拟; 右侧(b), (d), (f), (h)为加入600 A HCF产生的$ {A}_{//{\mathrm{H}}{\mathrm{C}}{\mathrm{F}}} $的模拟
Fig. 12. Temporal evolutions of the P-B mode spectrum structure considering HCF. From top to bottom, the sequences are the orginal equilibrium (a), (b); equilibrium with JLHW = 0.2 MA (c), (d); JLHW = 0.3 MA (e), (f); JLHW = 0.4 MA (g), (h), respectively. The left column (a), (c), (e), (g) represent cases without $ {A}_{//{\mathrm{H}}{\mathrm{C}}{\mathrm{F}}} $; the right column (b), (d), (f), (h) represent cases with $ {A}_{//{\mathrm{H}}{\mathrm{C}}{\mathrm{F}}} $ from 600 A HCF.
-
[1] Zohm H 1996 Plasma Phys. Control. Fusion 38 105
Google Scholar
[2] Leonard A W 2014 Phys. Plasmas 21 090501
Google Scholar
[3] Loarte A, Saibene G, Sartori R, et al. 2003 Plasma Phys. Control. Fusion 45 1549
Google Scholar
[4] Lang P T, Loarte A, Saibene G, et al. 2013 Nucl. Fusion 53 043004
Google Scholar
[5] Loarte A, Huijsmans G, Futatani S, et al. 2014 Nucl. Fusion 54 033007
Google Scholar
[6] Hughes J W, Hubbard A E, Wallace G, et al. 2010 Nucl. Fusion 50 064001
Google Scholar
[7] Wan B, Li J, Guo H, Liang Y, Xu G, Gong X Z for the EAST Team, International Collaborators 2013 Nucl. Fusion 53 104006
Google Scholar
[8] Rossel J X, Moret J M, Coda S, Sauter O, Goodman T P, Felici F, Testa D, Martin Y 2012 Nucl. Fusion 52 032004
Google Scholar
[9] Felici F, Rossel J X, Duval B P, Coda S, Goodman T P, Martin Y, Moret J M, Sauter O, the TCV Team 2013 Nucl. Fusion 53 113018
Google Scholar
[10] Baylor L R, Commaux N, Jernigan T C, et al. 2013 Phys. Rev. Lett. 110 245001
Google Scholar
[11] Chen S Y, Huang J, Sun T T, Wang Z H, Tang C J 2014 Phys. Plasmas 21 112512
Google Scholar
[12] Evans T E, Moyer R A, Watkins J G, et al. 2005 J. Nucl. Mater. 337–339 691
Google Scholar
[13] Canik J M, Maingi R, Evans T E, et al. 2010 Nucl. Fusion 50 034012
Google Scholar
[14] Xiao W W, Diamond P H, Zou X L, et al. 2012 Nucl. Fusion 52 114027
Google Scholar
[15] Huang J, Chen S Y, Wang Z H, Tang C J 2015 Phys. Plasmas 22 122507
Google Scholar
[16] Degeling A W, Martin Y R, Lister J B, Villard L, Dokouka V N, Lukash V E, Khayrutdinov R R 2003 Plasma Phys. Control. Fusion 45 1637
Google Scholar
[17] Wu N, Chen S Y, Song X M, Mou M L, Huang J, Wang Z T, Tang C J, Song X, Xia F, Jiang M, HL-2A Team 2017 Phys. Plasmas 24 092507
Google Scholar
[18] Zhang H M, Wu J, Li J X, Yao L M, Xu J C, Wu Y Z, Liu Q Y, Guo P C 2021 Acta Phys. Sin. 70 235203
Google Scholar
[19] 刘冠男, 李新霞, 刘洪波, 孙爱萍 2023 72 245202
Google Scholar
Liu G N, Li X X, Liu H B, Sun A P 2023 Acta Phys. Sin. 72 245202
Google Scholar
[20] Zhou T T, Xiang N, Gan C Y, Jia G Z, Chen J L 2022 Chin. Phys. B 31 095201
Google Scholar
[21] Xu Z, Wu Z W, Zhang L, Huang Y H, Gao W, Cheng Y X, Lin X D, Gao X, Chen Y J, Li L, Jie Y X, Zang Q, Liu H Q, EAST Team 2021 Chin. Phys. B 30 075205
Google Scholar
[22] Liang Y, Gong X Z, Gan K F, et al. 2013 Phys. Rev. Lett. 110 235002
Google Scholar
[23] Xiao G L, Zhong W L, Zou X L, et al. 2017 Phys. Plasmas 24 122507
Google Scholar
[24] Cui B T, Ji X Q, Sun T F, Liang S Y, Zhang J Z, Wang A, He M Y 2021 Fusion Eng. Des. 173 112963
Google Scholar
[25] Li S H, Wang N C, Ding Y H, et al. 2022 Plasma Phys. Control. Fusion 64 075005
Google Scholar
[26] Snyder P B, Wilson H R, Ferron J R, Lao L L, Leonard A W, Osborne T H, Turnbull A D, Mossessian D, Murakami M, Xu X Q 2002 Phys. Plasmas 9 2037
Google Scholar
[27] Bernard L C, Helton F J, Moore R W 1981 Comput. Phys. Commun. 24 377
Google Scholar
[28] Pankin A Y, Bateman G, Brennan D P, Kritz A H, Kruger S, Snyder P B, Sovinec C, the NIMROD Team 2007 Plasma Phys. Control. Fusion 49 S63
Google Scholar
[29] Pamela S J P, Huijsmans G T A, Eich T, et al. 2017 Nucl. Fusion 57 076006
Google Scholar
[30] Dudson B D, Umansky M V, Xu X Q, Snyder P B, Wilson H R 2009 Comput. Phys. Commun. 180 1467
Google Scholar
[31] Xu X Q, Dudson B, Snyder P B, Umansky M V, Wilson H 2010 Phys. Rev. Lett. 105 175005
Google Scholar
[32] Xia T Y, Xu X Q 2013 Phys. Plasmas 20 052102
Google Scholar
[33] Xia T Y, Xu X Q, Xi P W 2013 Nucl. Fusion 53 073009
Google Scholar
[34] Mou M L, Huang J, Wu N, Chen S Y, Tang C J 2016 Phys. Lett. A 380 2544
Google Scholar
[35] Dong L K, Chen S Y, Mou M L, Tang C J 2020 Plasma Sci. Technol. 22 115101
Google Scholar
[36] Huang J, Chen S Y, Tang C J 2016 Phys. Plasmas 23 052513
Google Scholar
[37] Xia T Y, Gui B, Huang Y Q, Wu Y B, Xiao X T, EAST Team 2019 Nucl. Fusion 59 076043
Google Scholar
[38] Shi Y J, Xu G S, Wang F D, et al. 2011 Phys. Rev. Lett. 106 235001
Google Scholar
[39] Rice J E, Podpaly Y A, Reinke M L, et al. 2013 Nucl. Fusion 53 093015
Google Scholar
[40] Chouli B, Fenzi C, Garbet X, et al. 2014 Plasma Phys. Control. Fusion 56 095018
Google Scholar
[41] Chen W, Wang Z X 2020 Chin. Phys. Lett. 37 125001
Google Scholar
[42] Fisch N J, Rax J M 1992 Phys. Rev. Lett. 69 612
Google Scholar
[43] Smirnov A P, Harvey R W 2001 The GENRAY Ray Tracing Code CompX Report No. CompX-2000-01
[44] Ehst D A, Karney C F F 1991 Nucl. Fusion 31 1933
Google Scholar
[45] Crotinger J A, LoDestro L, Pearlstein L D, Tarditi A, Casper T A, Hooper E B 1997 CORSICA: A Comprehensive Simulation of Toroidal Magnetic-fusion Devices. Final Report to the LDRD Program (Livermore: Lawrence Livermore National Lab.) Report No: UCRL-ID-126284
[46] Xu X Q, Ma J F, Li G Q 2014 Phys. Plasmas 21 120704
Google Scholar
[47] Burrell K H 1997 Phys. Plasmas 4 1499
Google Scholar
[48] Ding B J, Bonoli P T, Tuccillo A, et al. 2018 Nucl. Fusion 58 095003
Google Scholar
[49] Li G Q, Xu X Q, Snyder P B, Turnbull A D, Xia T Y, Ma C H, Xi P W 2014 Phys. Plasmas 21 102511
Google Scholar
[50] Zhang Y, Huang J, Chen S Y, Tang C J 2017 Phys. Plasmas 24 062108
Google Scholar
[51] Li J, Guo H Y, Wan B N, et al. 2013 Nat. Phys. 9 817
Google Scholar
[52] Dong L K, Chen S Y, Mou M L, Luo Y, Qin C C, Tang C J 2023 Nucl. Fusion 63 086023
Google Scholar
[53] Liu Y, Ham C J, Kirk A, Li L, Loarte A, Ryan D A, Sun Y, Suttrop W, Yang X, Zhou L 2016 Plasma Phys. Control. Fusion 58 114005
Google Scholar
[54] Oyama N, Sakamoto Y, Isayama A, et al. 2005 Nucl. Fusion 45 871
Google Scholar
[55] Aiba N, Giroud C, Honda M, et al. 2017 Nucl. Fusion 57 126001
Google Scholar
[56] Luo Y, Chen S Y, Huang J, Xiong Y Y, Tang C J 2016 Phys. Plasmas 23 042302
Google Scholar
[57] Xi P W, Xu X Q, Wang X G, Xia T Y 2012 Phys. Plasmas 19 092503
Google Scholar
[58] 李春雨, 郝广周, 刘钺强, 王炼, 刘艺慧子 2022 71 075202
Google Scholar
Li C Y, Hao G Z, Liu Y Q, Wang L, Liu Y H Z 2022 Acta Phys. Sin. 71 075202
Google Scholar
下载:
计量
- 文章访问数: 1666
- PDF下载量: 43
- 被引次数: 0
