电致伸缩效应下水中电子输运特性

李元; 李春鹏; 李林波; 袁磊; 王亚桢; 石亚轩; 张冠军

doi:10.7498/aps.73.20231893

摘要

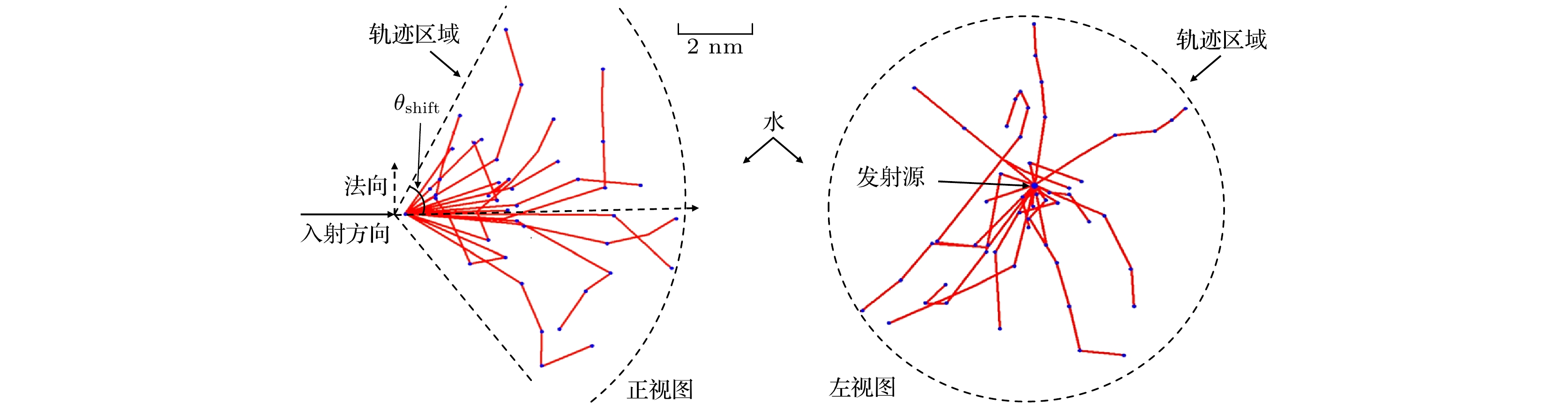
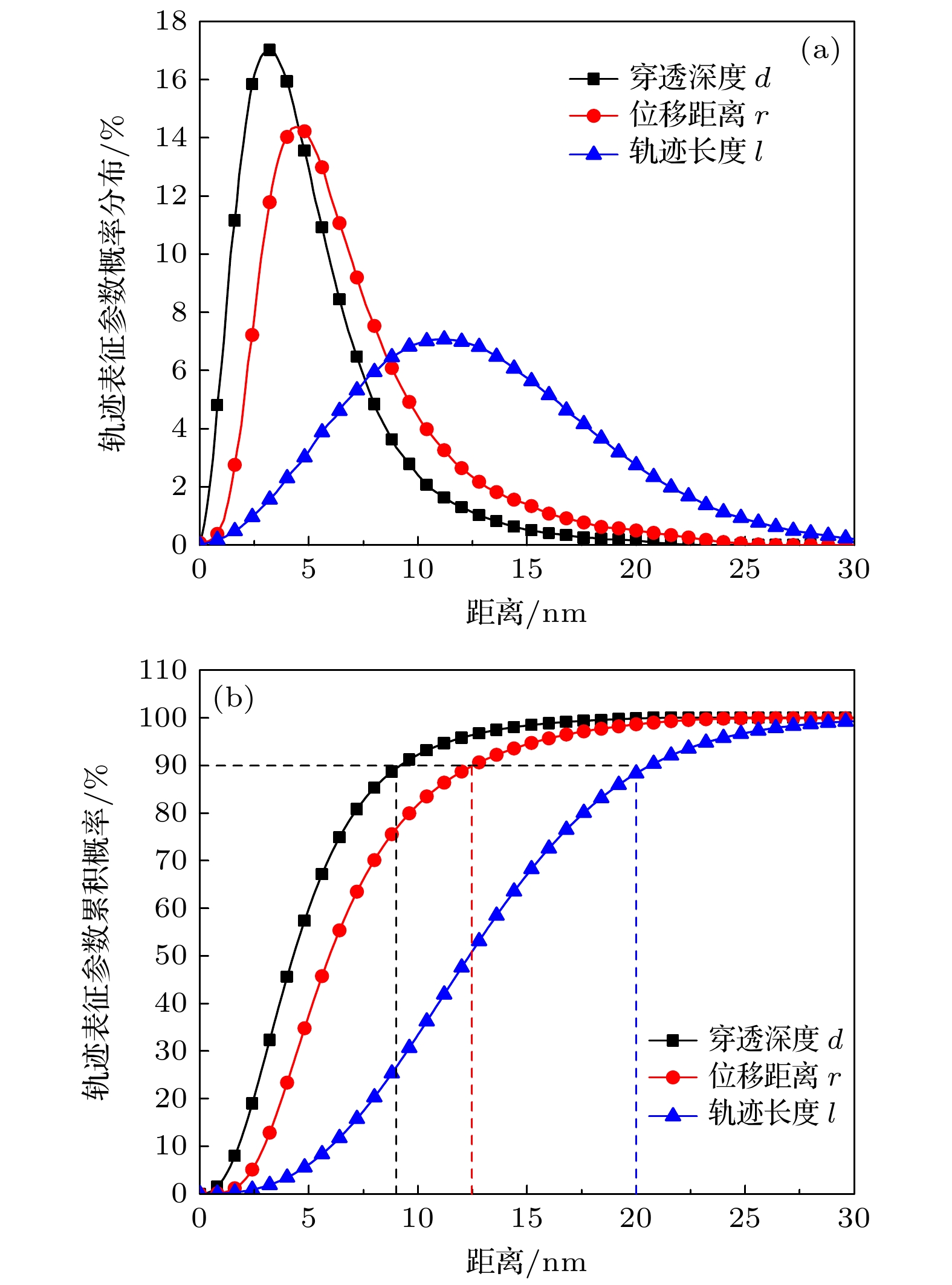
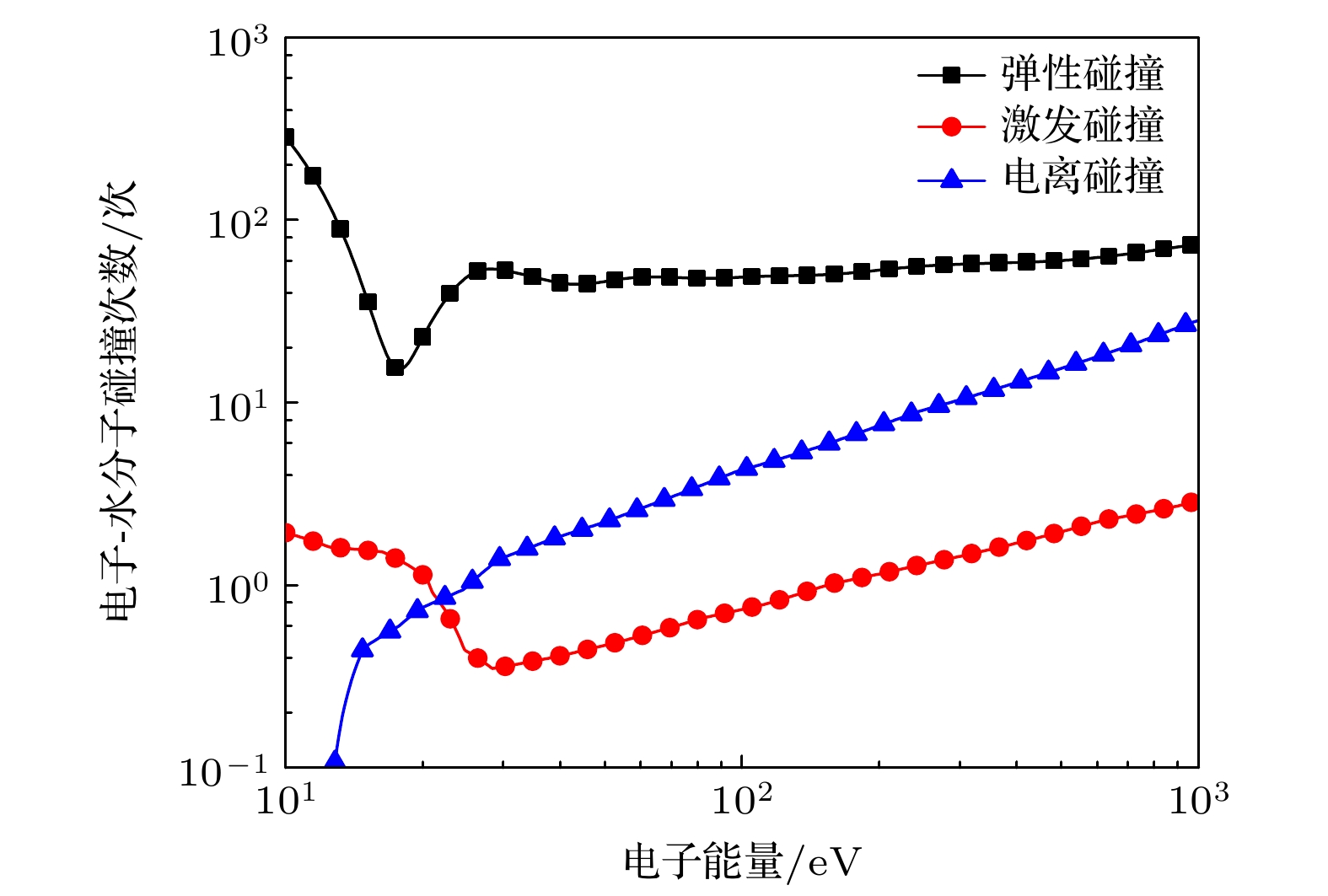
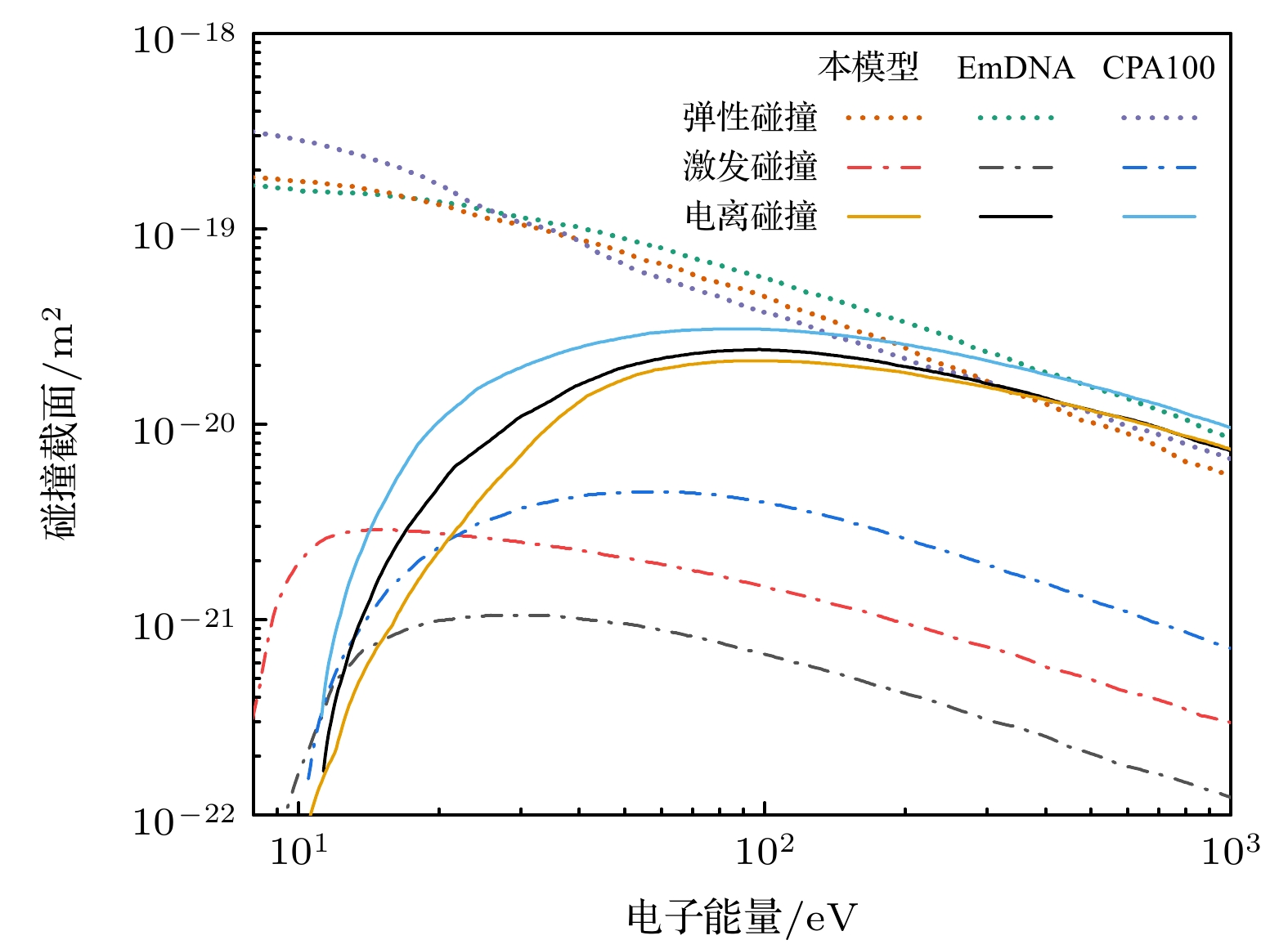
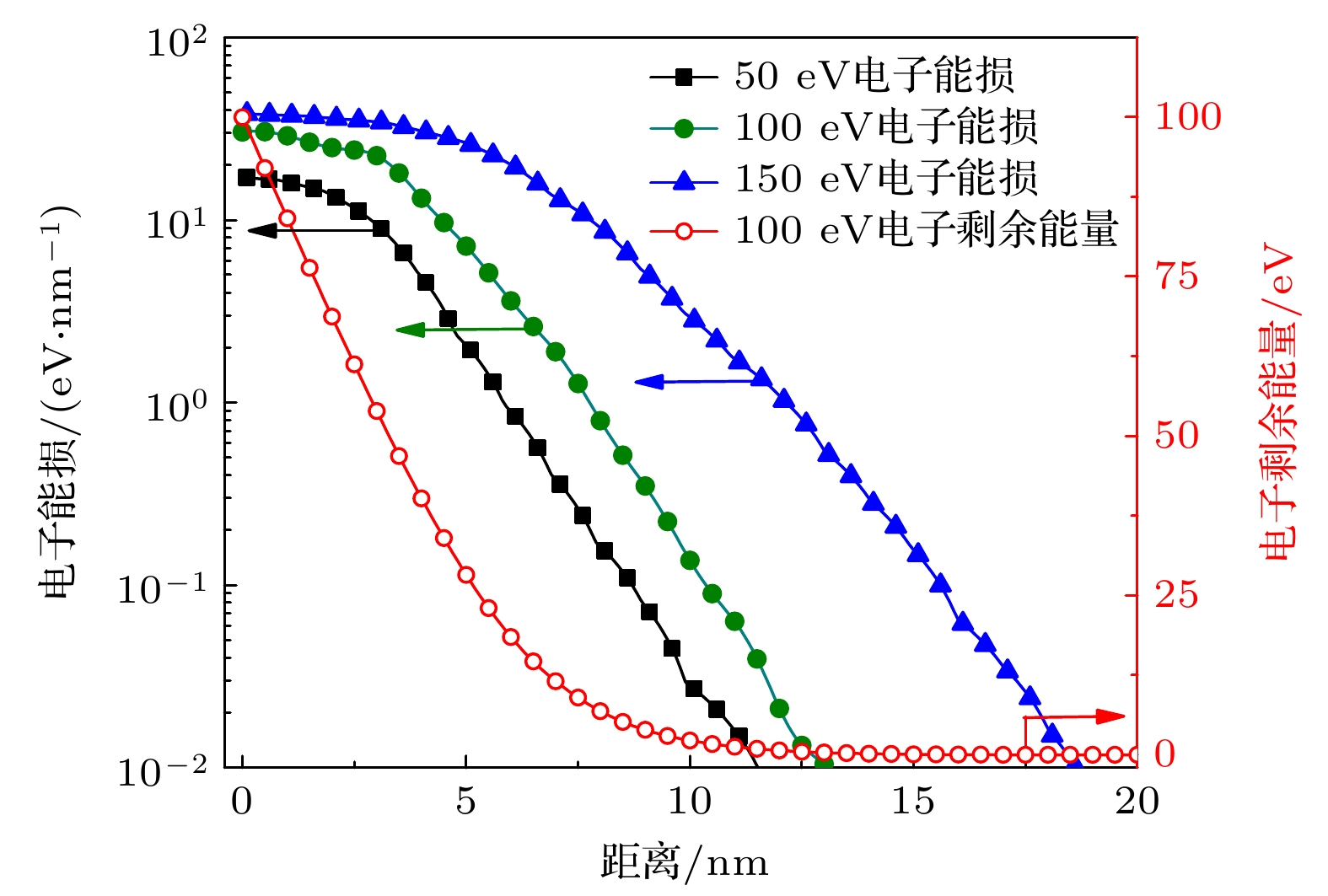
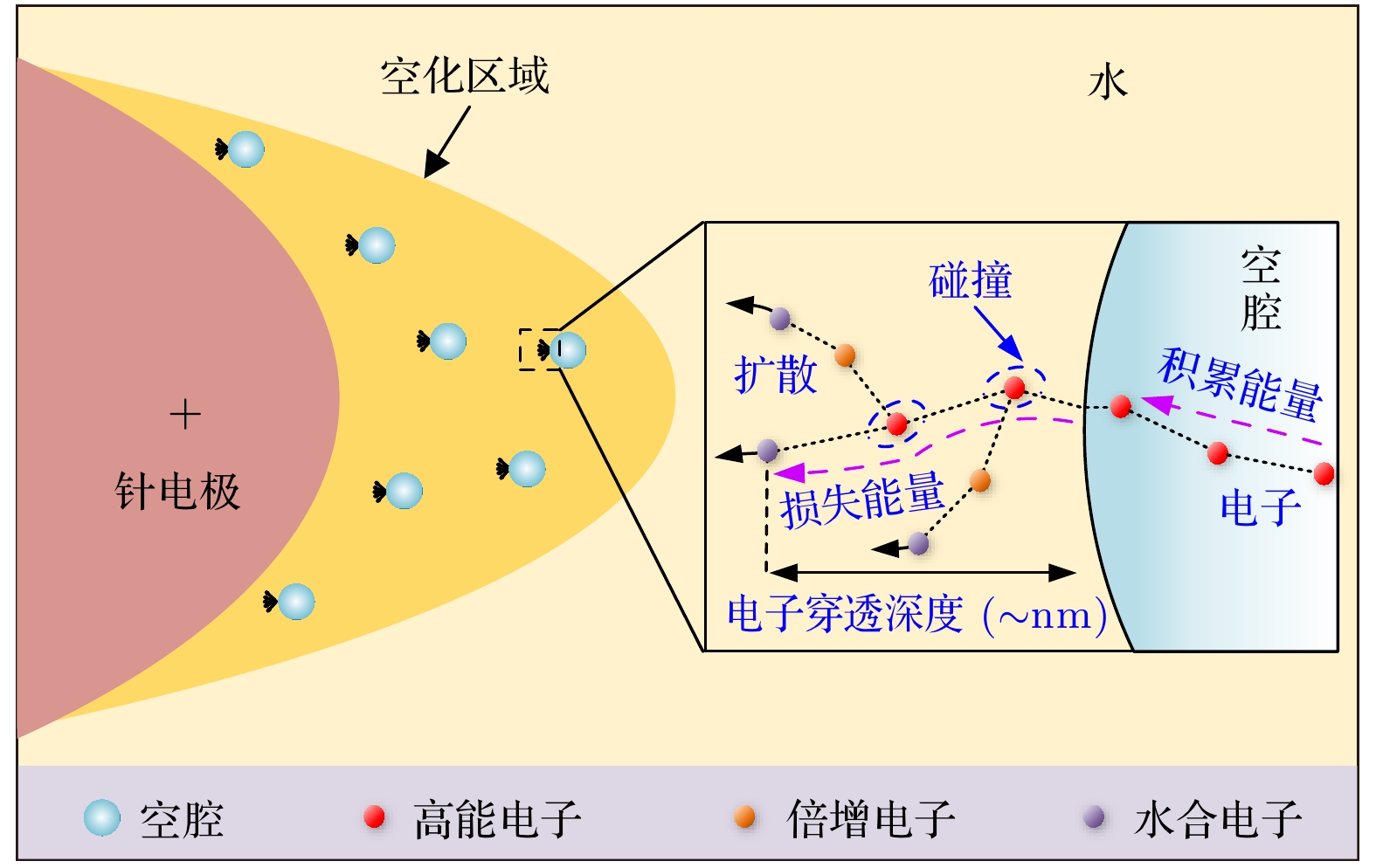
水中快脉冲(脉宽数ns甚至ps级)放电过程中, 快脉冲在电极附近引起电致伸缩效应导致电极附近形成空化区. 电子在空化区内积累能量并高速进入水体, 电子在水中的输运特性是水中脉冲放电起始与发展的关键因素. 本文构建了考虑弹性与非弹性碰撞截面的水中电子输运物理模型, 采用蒙特卡罗方法研究不同能量电子的透射与散射径迹结构特征, 研究了弹性碰撞、电离与激发碰撞频次随电子初始能量的变化以及水中电子能量损失特征. 结果表明, 较低能量的电子(约20 eV)受水分子散射影响能量损失较大, 透射能力较弱, 随着电子初始能量的增高, 电子受水分子散射作用的影响逐渐减小, 具有更强的液体穿透能力; 弹性碰撞次数远大于激发与电离碰撞, 导致电子散射距离与透射深度相当, 电离碰撞和激发碰撞次数随电子能量升高显著增加; 电子入射能量越高, 其能损越大, 随运动距离增加, 能损急剧下降, 与电子的平均电离能量损失W变化趋势一致. 本研究可为探究快脉冲放电机理提供重要数据基础.

关键词:

Abstract

The transport characteristics of electrons are crucial for the initiation and development of pulse discharge in water. In this work, we develop a physical model of electron transport that consides elastic and inelastic collision cross sections. The purpose of this study is to investigate frequency variations of elastic collisions, ionization and excitation collisions with different initial electron energy values, and to explore the characteristic of electron energy loss in water. The Monte Carlo method is employed to track structure characteristics of electron transmission and scattering under varying energy values. The results show that the electrons of lower energy (~20 eV) are significantly impacted by the water molecule scattering, hence their transmission capacities are weakened. When the incident energy of electron reaches 100 eV, the scattering deviation distance is roughly equivalent to the transmission depth, about 6–8 nm, and the maximum deviation angle θ_shift ~ 60°. When the electron incident energy is in a range of 10–1000 eV, the number of elastic collisions is much greater than the number of excitation and ionization collisions, and the number of ionization collisions and excitation collisions increases significantly with the increase of electron energy. The higher the electron incident energy, the greater the energy loss is. However, the energy loss decreases sharply with the extension of penetration distance. For the ionization collision, the average ionization energy loss, W, decreases rapidly with the increase of electron energy, and ultimately maintains at a level of 20–30 eV, which is consistent with the experimental results reported.

Keywords:

作者及机构信息

西安交通大学电气工程学院, 西安　710049

通信作者: 李元, liyuan8490@xjtu.edu.cn

基金项目: 国家自然科学基金(批准号: 52041702)资助的课题.

Authors and contacts

School of Electrical Engineering, Xi’an Jiaotong University, Xi’an 710049, China

Corresponding author: Li Yuan, liyuan8490@xjtu.edu.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant No. 52041702).

文章全文 : translate this paragraph

参考文献

[1]	赵景林, 王志强, 王进君, 张东东, 李国锋 2023 强激光与粒子束 35 035005 Google Scholar Zhao J L, Wang Z Q, Wang J J, Zhang D D, Li G F 2023 High Power Laser Part. Beams 35 035005 Google Scholar
[2]	Wang L R, Wen X Q, Yang Y T, Wang X 2023 J. Appl. Phys. 134 013302 Google Scholar
[3]	李显东, 刘毅, 周古月, 刘思维, 李志远, 林福昌, 潘垣 2018 中国电机工程学报 38 1562 Google Scholar Li X D, Liu Y, Zhou G Y, Liu S W, Li Z Y, Lin F C, Pan Y 2018 Proceeding of the CSEE 38 1562 Google Scholar
[4]	尤特金 1962 液电效应 (北京: 科学出版社) 第45—50页 Yutkin 1962 Electro-hydraulic Effect (Beijing: Science Press) pp45–50
[5]	李元, 李林波, 温嘉烨, 倪正全, 张冠军 2021 70 024701 Google Scholar Li Y, Li L B, Wen J Y, Ni Z Q, Zhang G J 2021 Acta Phys. Sin. 70 024701 Google Scholar
[6]	Seepersad Y, Pekker M, Shneider M N, Fridman A, Dobrynin D 2013 J. Appl. Phys. 46 355201 Google Scholar
[7]	Shneider M, Pekker M, Fridman A 2012 IEEE Trans. Dielectr. Electr. Insul. 19 1579 Google Scholar
[8]	Shneider M N, Pekker M 2013 J. Appl. Phys. 114 214906 Google Scholar
[9]	Pekker M, Shneider M N 2017 Fluid Dyn. Res. 49 035503 Google Scholar
[10]	Aghdam A C, Farouk T 2020 Plasma Sources Sci. Technol. 29 025011 Google Scholar
[11]	涂婧怡, 陈赦, 汪沨 2019 68 095202 Google Scholar Tu J Y, Chen S, Wang F 2019 Acta Phys. Sin. 68 095202 Google Scholar
[12]	张晋琪, 蒋兴良, 陈志刚 2006 强激光与粒子束 1 18 1053 Zhang J Q, Jiang X L, Chen Z G 2006 High Power Laser Part. Beams 18 1053
[13]	李元, 温嘉烨, 李林波, 郜晶, 石亚轩, 刘志濠, 张冠军 2021 强激光与粒子束 33 065001 Google Scholar Li Y, Wen J Y, Li L B, Gao J, Shi Y X, Liu Z H Zhang G J 2021 High Power Laser Part. Beams 33 065001 Google Scholar
[14]	Chen X, Li, C, Ke K 2017 Chin. Sci. Bull. 62 2866 Google Scholar
[15]	Wen X Q, Zhou Y B, Xue X D, Yang Y T 2021 Phys. Plasmas 28 013507 Google Scholar
[16]	Yang Y T, Wen X Q, Wang L R, Wang X 2022 Phys. Plasmas 29 093501 Google Scholar
[17]	尹昊, 宋通, 彭雄刚, 张鹏, 于润升, 陈喆, 曹兴忠, 王宝义 2023 72 114101 Google Scholar Yin H, Song T, Peng X G, Zhang P, Yu R S, Chen Z, Cao X Z, Wang B Y 2023 Acta Phys. Sin. 72 114101 Google Scholar
[18]	赵喆, 卢岳, 张振华, 隋曼龄 2019 物理化学学报 35 539 Google Scholar Zhao Z, Lu Y, Zhang Z H, Sui M L 2019 Acta Phys. -Chim. Sin. 35 539 Google Scholar
[19]	Damascelli A, Hussain Z, Shen Z X 2003 Rev. Mod. Phys. 75 473 Google Scholar
[20]	赵林, 刘国东, 周兴江 2021 70 017406 Google Scholar Zhao L, Liu G D, Zhou X J 2021 Acta Phys. Sin. 70 017406 Google Scholar
[21]	Bousis C, Emfietzoglou D, Hadjidoukas P, Nikjoo H, Pathak A 2008 Nucl. Instrum. Methods Phys. Res. Sect. B 266 1185 Google Scholar
[22]	Dingfelder M, Ritchie R H, Turner J E, Friedland W, Paretzke H G, Hamm R N 2008 Radiat. Res. 169 584 Google Scholar
[23]	Bordage M C, Bordes J, Edel S, Terrissol M, Franceries X, Bardiès M, Lampe N, Incerti S 2016 Physica Med. 32 1833 Google Scholar
[24]	谭震宇, 张黎明, 王晶, 高洪霞 2012 电工技术学报 27 1 Google Scholar Tan Z Y, Zhang L M, Wang J, Gao H X, 2012 Trans. Chin. Electrotech. Soc. 27 1 Google Scholar
[25]	Uehara S, Nikjoo H, Goodhead D T 1992 Phys. Med. Biol. 37 1841 Google Scholar
[26]	Emfietzoglou D, Papamichael G, Androulidaki I, Karava K, Kostarelos K, Pathak A, Moscovitch M 2005 Nucl. Instrum. Methods Phys. Res. , Sect. B 228 341 Google Scholar
[27]	Dingfelder M, Hantke D, Inokuti M, Paretzke H G 1998 Radiat. Phys. Chem. 53 1 Google Scholar
[28]	Fernandez-Varea J M, Mayol R, Liljequist D, Salvat F 1993 J. Phys. Condens. Matter 5 3593 Google Scholar
[29]	Vriens L 1966 Phys. Rev. 141 88 Google Scholar
[30]	Emfietzoglou D, Nikjoo H A 2007 Radiat. Res. 167 110 Google Scholar
[31]	Choi E, Chon K S, Yoon M G 2020 Radiat. Eff. Defects Solids 175 11
[32]	Incerti S, Kyriakou I, Tran H N 2017 Nucl. Instrum. Methods Phys. Res. , Sect. B B 397 45 Google Scholar
[33]	李林波 2021 硕士学位论文 (西安: 西安交通大学) Li L B 2021 M. S. Thesis (Xi'an: Xi'an Jiaotong University
[34]	Wang D, Namihira T 2020 Plasma Sources Sci. Technol. 29 023001 Google Scholar
[35]	Emfietzoglou D 2003 Radiat. Phys. Chem. 66 373 Google Scholar
[36]	Combecher D 1980 Radiat. Res. 84 189 Google Scholar

施引文献

图 1 电致伸缩作用下液态水空化及电子–水分子碰撞过程^[5]

Fig. 1. Cavitation of liquid water and electron–water collision process under electrostriction^[5].

下载: 全尺寸图片幻灯片

图 2 水中电子输运仿真流程

Fig. 2. Simulation flow chart of electronic transport in water

下载: 全尺寸图片幻灯片

图 3 电子入射水体过程示意

Fig. 3. Schematic diagram of electron ejection into water bulk.

下载: 全尺寸图片幻灯片

图 4 水中电子运动轨迹的正视图及左视图(E = 100 eV)

Fig. 4. Front and left views of electron trajectories in water (E = 100 eV).

下载: 全尺寸图片幻灯片

图 5 电子轨迹表征参数l, r, d的统计　(a) 概率分布; (b) 累积概率

Fig. 5. Statistics of electron trajectory characterization parameters l, r and d: (a) Probability distribution; (b) cumulative probability.

下载: 全尺寸图片幻灯片

图 6 不同电子能量下的轨迹表征参数

Fig. 6. Trajectory characterization parameters under different electron energies.

下载: 全尺寸图片幻灯片

图 7 不同能量下的电子平均自由程

Fig. 7. Average free path of electrons at different energies.

下载: 全尺寸图片幻灯片

图 8 不同电子能量下的弹性碰撞、激发碰撞与电离碰撞次数

Fig. 8. Collision times of elasticity, excitation and ionization at different electron energies.

下载: 全尺寸图片幻灯片

图 9 不同模型下电子-水分子弹性、电离与激发碰撞截面

Fig. 9. Cross sections of electron-water molecule due to elastic, ionization, and excitation collision derived by varying models.

下载: 全尺寸图片幻灯片

图 10 电子能损与电子剩余能量

Fig. 10. Energy consumption rate and residual energy of electron.

下载: 全尺寸图片幻灯片

图 11 电子-水分子激发、电离碰撞数量占比及消耗能量占比

Fig. 11. Number proportion and energy consumption proportion of electron-water molecule excitation and ionization collision.

下载: 全尺寸图片幻灯片

图 12 不同电子能量下的W值

Fig. 12. W values at different electron energies.

下载: 全尺寸图片幻灯片

表 1 电离能级与激发能级参数

Table 1. Ionization levels and excitation level parameters

电离能级	B_j (j = 1, 2···, 5)/eV	U_j (j = 1, 2···, 5)/eV	激发能级	E_j (j = 6, 7···, 10)/eV
1b₁	10	30	A¹B₁	8.40
3a₁	13	40	B¹A₁	10.10
1b₂	17	50	Ryd A+B	11.26
2a₁	32.2	60	Ryd C+D	11.93
1a₁	539.7	700	Diffuse bands	14.10

下载: 导出CSV

map

[1]	赵景林, 王志强, 王进君, 张东东, 李国锋 2023 强激光与粒子束 35 035005 Google Scholar Zhao J L, Wang Z Q, Wang J J, Zhang D D, Li G F 2023 High Power Laser Part. Beams 35 035005 Google Scholar
[2]	Wang L R, Wen X Q, Yang Y T, Wang X 2023 J. Appl. Phys. 134 013302 Google Scholar
[3]	李显东, 刘毅, 周古月, 刘思维, 李志远, 林福昌, 潘垣 2018 中国电机工程学报 38 1562 Google Scholar Li X D, Liu Y, Zhou G Y, Liu S W, Li Z Y, Lin F C, Pan Y 2018 Proceeding of the CSEE 38 1562 Google Scholar
[4]	尤特金 1962 液电效应 (北京: 科学出版社) 第45—50页 Yutkin 1962 Electro-hydraulic Effect (Beijing: Science Press) pp45–50
[5]	李元, 李林波, 温嘉烨, 倪正全, 张冠军 2021 70 024701 Google Scholar Li Y, Li L B, Wen J Y, Ni Z Q, Zhang G J 2021 Acta Phys. Sin. 70 024701 Google Scholar
[6]	Seepersad Y, Pekker M, Shneider M N, Fridman A, Dobrynin D 2013 J. Appl. Phys. 46 355201 Google Scholar
[7]	Shneider M, Pekker M, Fridman A 2012 IEEE Trans. Dielectr. Electr. Insul. 19 1579 Google Scholar
[8]	Shneider M N, Pekker M 2013 J. Appl. Phys. 114 214906 Google Scholar
[9]	Pekker M, Shneider M N 2017 Fluid Dyn. Res. 49 035503 Google Scholar
[10]	Aghdam A C, Farouk T 2020 Plasma Sources Sci. Technol. 29 025011 Google Scholar
[11]	涂婧怡, 陈赦, 汪沨 2019 68 095202 Google Scholar Tu J Y, Chen S, Wang F 2019 Acta Phys. Sin. 68 095202 Google Scholar
[12]	张晋琪, 蒋兴良, 陈志刚 2006 强激光与粒子束 1 18 1053 Zhang J Q, Jiang X L, Chen Z G 2006 High Power Laser Part. Beams 18 1053
[13]	李元, 温嘉烨, 李林波, 郜晶, 石亚轩, 刘志濠, 张冠军 2021 强激光与粒子束 33 065001 Google Scholar Li Y, Wen J Y, Li L B, Gao J, Shi Y X, Liu Z H Zhang G J 2021 High Power Laser Part. Beams 33 065001 Google Scholar
[14]	Chen X, Li, C, Ke K 2017 Chin. Sci. Bull. 62 2866 Google Scholar
[15]	Wen X Q, Zhou Y B, Xue X D, Yang Y T 2021 Phys. Plasmas 28 013507 Google Scholar
[16]	Yang Y T, Wen X Q, Wang L R, Wang X 2022 Phys. Plasmas 29 093501 Google Scholar
[17]	尹昊, 宋通, 彭雄刚, 张鹏, 于润升, 陈喆, 曹兴忠, 王宝义 2023 72 114101 Google Scholar Yin H, Song T, Peng X G, Zhang P, Yu R S, Chen Z, Cao X Z, Wang B Y 2023 Acta Phys. Sin. 72 114101 Google Scholar
[18]	赵喆, 卢岳, 张振华, 隋曼龄 2019 物理化学学报 35 539 Google Scholar Zhao Z, Lu Y, Zhang Z H, Sui M L 2019 Acta Phys. -Chim. Sin. 35 539 Google Scholar
[19]	Damascelli A, Hussain Z, Shen Z X 2003 Rev. Mod. Phys. 75 473 Google Scholar
[20]	赵林, 刘国东, 周兴江 2021 70 017406 Google Scholar Zhao L, Liu G D, Zhou X J 2021 Acta Phys. Sin. 70 017406 Google Scholar
[21]	Bousis C, Emfietzoglou D, Hadjidoukas P, Nikjoo H, Pathak A 2008 Nucl. Instrum. Methods Phys. Res. Sect. B 266 1185 Google Scholar
[22]	Dingfelder M, Ritchie R H, Turner J E, Friedland W, Paretzke H G, Hamm R N 2008 Radiat. Res. 169 584 Google Scholar
[23]	Bordage M C, Bordes J, Edel S, Terrissol M, Franceries X, Bardiès M, Lampe N, Incerti S 2016 Physica Med. 32 1833 Google Scholar
[24]	谭震宇, 张黎明, 王晶, 高洪霞 2012 电工技术学报 27 1 Google Scholar Tan Z Y, Zhang L M, Wang J, Gao H X, 2012 Trans. Chin. Electrotech. Soc. 27 1 Google Scholar
[25]	Uehara S, Nikjoo H, Goodhead D T 1992 Phys. Med. Biol. 37 1841 Google Scholar
[26]	Emfietzoglou D, Papamichael G, Androulidaki I, Karava K, Kostarelos K, Pathak A, Moscovitch M 2005 Nucl. Instrum. Methods Phys. Res. , Sect. B 228 341 Google Scholar
[27]	Dingfelder M, Hantke D, Inokuti M, Paretzke H G 1998 Radiat. Phys. Chem. 53 1 Google Scholar
[28]	Fernandez-Varea J M, Mayol R, Liljequist D, Salvat F 1993 J. Phys. Condens. Matter 5 3593 Google Scholar
[29]	Vriens L 1966 Phys. Rev. 141 88 Google Scholar
[30]	Emfietzoglou D, Nikjoo H A 2007 Radiat. Res. 167 110 Google Scholar
[31]	Choi E, Chon K S, Yoon M G 2020 Radiat. Eff. Defects Solids 175 11
[32]	Incerti S, Kyriakou I, Tran H N 2017 Nucl. Instrum. Methods Phys. Res. , Sect. B B 397 45 Google Scholar
[33]	李林波 2021 硕士学位论文 (西安: 西安交通大学) Li L B 2021 M. S. Thesis (Xi'an: Xi'an Jiaotong University
[34]	Wang D, Namihira T 2020 Plasma Sources Sci. Technol. 29 023001 Google Scholar
[35]	Emfietzoglou D 2003 Radiat. Phys. Chem. 66 373 Google Scholar
[36]	Combecher D 1980 Radiat. Res. 84 189 Google Scholar

[1]	陈小明, 李国荣. BaTiO₃基无铅陶瓷大电致伸缩系数. , 2022, 71(16): 167701. doi: 10.7498/aps.71.20220451
[2]	张硕, 龙连春, 刘静毅, 杨洋. 缺陷对铁单质薄膜磁致伸缩与磁矩演化的影响. , 2022, 71(1): 017502. doi: 10.7498/aps.71.20211177
[3]	李元, 李林波, 温嘉烨, 倪正全, 张冠军. 基于电致伸缩效应的水中纳秒脉冲放电起始机制. , 2021, 70(2): 024701. doi: 10.7498/aps.70.20201048
[4]	张超, 方粮, 隋兵才, 徐强, 王慧. 基于微芯片的透射电子显微镜的低温纳米精度电子束刻蚀与原位电学输运性质测量. , 2014, 63(24): 248105. doi: 10.7498/aps.63.248105
[5]	屈少华, 曹万强. 球形无规键无规场模型研究弛豫铁电体极化效应. , 2014, 63(4): 047701. doi: 10.7498/aps.63.047701
[6]	沙金, 包伯成, 许建平, 高玉. 脉冲序列控制电流断续模式Buck变换器的动力学建模与边界碰撞分岔. , 2012, 61(12): 120501. doi: 10.7498/aps.61.120501
[7]	李川, 刘敬华, 陈立彪, 蒋成保, 徐惠彬. Fe81Ga19合金晶体生长取向与磁致伸缩性能. , 2011, 60(9): 097505. doi: 10.7498/aps.60.097505
[8]	姜永恒, 孙成林, 李占龙, 曹安阳, 里佐威. 苯C—H伸缩振动弱增益模式的受激拉曼散射. , 2011, 60(6): 064211. doi: 10.7498/aps.60.064211
[9]	陈艳荣, 王培杰, 方炎. 亚乙基硫脲分子键伸缩模式与全耦合模式键极化率的对比及其拉曼激发虚态的相关研究. , 2010, 59(9): 6052-6058. doi: 10.7498/aps.59.6052
[10]	王小炼, 冯灏, 孙卫国, 樊群超, 曾阳阳, 王斌. 低能电子与H2分子碰撞振动激发动量迁移散射截面的研究. , 2010, 59(2): 937-942. doi: 10.7498/aps.59.937
[11]	周可余, 叶辉, 甄红宇, 尹伊, 沈伟东. 基于压电聚合物薄膜可调谐Fabry-Perot滤波器的研究. , 2010, 59(1): 365-369. doi: 10.7498/aps.59.365
[12]	卞雷祥, 文玉梅, 李平. 磁致伸缩/压电叠层复合材料磁-机-电耦合系数分析. , 2009, 58(6): 4205-4213. doi: 10.7498/aps.58.4205
[13]	王斌, 冯灏, 孙卫国, 曾阳阳, 戴伟. 低能电子与氢分子碰撞的振动激发积分散射截面的研究. , 2009, 58(10): 6932-6937. doi: 10.7498/aps.58.6932
[14]	高剑森, 张宁. 异型磁体/铁电复合材料中的电致变磁导及电致变阻抗效应. , 2009, 58(12): 8607-8611. doi: 10.7498/aps.58.8607
[15]	戴伟, 冯灏, 孙卫国, 唐永建, 申立, 于江周. 用振动密耦合方法研究低能电子与N2分子碰撞的振动激发微分散射截面. , 2008, 57(1): 143-148. doi: 10.7498/aps.57.143
[16]	卢新培, 潘垣, 张寒虹. 水中脉冲放电的电特性与声辐射特性研究. , 2002, 51(7): 1549-1553. doi: 10.7498/aps.51.1549
[17]	李养贤, 曲静萍, 王博文, 徐桂芝, 于慧, 杨庆新, 颜威利, 吴光恒, 王敬华, 唐成春, 詹文山. TbyDy1-y(Fe1-xTx)2(T=Al,Mn)的磁致伸缩与内禀磁致伸缩特性. , 1999, 48(13): 257-262. doi: 10.7498/aps.48.257.2
[18]	陈学俊, 玉岩, 李波, 邓新元. 电子与原子(分子)碰撞的反散射理论. , 1994, 43(11): 1759-1763. doi: 10.7498/aps.43.1759
[19]	张胜良, 翟宏如. 非平衡Fe-Pd合金的矫顽力与磁致伸缩. , 1991, 40(10): 1712-1716. doi: 10.7498/aps.40.1712
[20]	李家明. 电子与类锂离子碰撞激发. , 1980, 29(4): 419-428. doi: 10.7498/aps.29.419

计量

文章访问数: 1408
PDF下载量: 49
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板