-
准确获取海底声学参数对声场分析、声纳应用等具有重要意义. 反演是获取海底声学参数的重要手段之一. 为了避免反演中的多值问题, 地声反演往往尽量减少待反演参数, 多采用单层或双层水平不变地声模型, 反演后的声学参数仅能在有限频段应用, 难以同时应用于较宽频段. 本文以实验中浅地层剖面仪测量的海底沉积层分层结构为基础建立地声模型, 采用多物理量分步联合手段反演各沉积层声学参数, 并通过匹配场定位、后验概率分析、采样等手段对反演结果进行验证. 将反演结果与单层等效地声模型反演结果进行对比分析, 结果说明, 本文建立的多层水平变化海底声学参数更接近真实情况, 可以应用在较宽频段范围, 解释不同声学现象, 且精度更高.Sound propagation in shallow water is significantly influenced by geoacoustic properties. Estimating these geoacoustic parameters is essential for sound field analysis and sonar performance assessment. As a common practice, the seafloor is often treated as a single-layer or two-layer range-independent geoacoustic model to reduce the number of involved parameters. However, acoustic parameters inverted through these two geoacoustic models are typically limited in their applicability to a specific frequency range, thus posing challenges when applied across a broader frequency range. A range-dependent multi-layer geoacoustic model based on experimental measurements obtained with a sub-bottom profiler is proposed in this study. The inversion scheme combines three inversion methods to estimate geoacoustic parameters, considering the different sensitivities of geoacoustic parameters to different physical parameters within the acoustic field. Firstly, modal dispersion is used to invert the geoacoustic parameters of each layer, with the dispersion curve obtained through warping transform and the Wigner-Ville distribution. After that, both the localization using matched field processing and the dispersion curve fitting demonstrate the effectiveness of the inversion results for each layer, although the peak of the probability distribution of sound speed in the first layer is broader than in others. Secondly, matched field processing is employed to invert the geoacoustic parameters of the first layer. This method is based on the theory that as frequency increases, the depth of sound rays penetrating the seabed decreases, revealing changes in the first layer's sound speed with the seabed depth. Lastly, bottom attenuation coefficients at different frequencies are inverted by the transmission loss (TL), and a fitting relationship between the attenuation coefficient and the frequency is derived. The inversion results obtained by using the range-dependent multi-layer geoacoustic model are compared with results estimated by the single-layer geoacoustic model. The findings indicate that the transmission loss (TL) error from the range-dependent multi-layer geoacoustic model in this study is smaller than that from the single-layer geoacoustic model, especially in the lower frequency band. The range-dependent multi-layer geoacoustic model proves to be suitable for a broader frequency range, providing better precision in explaining various acoustic phenomena.
-
Keywords:
- broadband geoacoustic inversion /
- range-dependent multi-layer geoacoustic model /
- modal dispersion /
- transmission loss
[1] Taroudakis M I, Markaki M G 1998 J. Comput. Acoust. 6 167
Google Scholar
[2] 杨坤德 2003 博士学位论文 (西安: 西北工业大学)
Yang K D 2003 Ph. D. Dissertation (Xi’an: Northwestern Polytechnical University
[3] Cobo P P, Ranz G C 1989 J. Acoust. Soc. Am. 85 2388
Google Scholar
[4] Zhou J X 1985 J. Acoust. Soc. Am. 78 1003
Google Scholar
[5] 赵梅, 胡长青 2009 声学技术 28 104
Google Scholar
Zhao M, Hu C Q 2009 Tech. Acoust. 28 104
Google Scholar
[6] 李风华, 张仁和 2000 声学学报 25 297
Google Scholar
Li F H, Zhang R H 2000 Acta Acustica 25 297
Google Scholar
[7] Yang T C, Yoo K, Fialkowski L T 2007 J. Acoust. Soc. Am. 122 3338
Google Scholar
[8] 翁晋宝, 李风华, 郭永刚 2015 声学学报 40 207
Google Scholar
Weng J B, Li F H, Guo Y G 2015 Acta Acustica 40 207
Google Scholar
[9] Li Z L, Zhang R H 2004 Chin. Phys. Lett. 21 1100
Google Scholar
[10] 李梦竹, 李整林, 周纪浔, 张仁和 2019 68 094301
Google Scholar
Li M Z, Li Z L, Zhou J X, Zhang R H 2019 Acta Phys. Sin. 68 094301
Google Scholar
[11] 吴双林 2016 硕士学位论文 (北京: 中国科学院声学研究所)
Wu S L 2016 M. S. Thesis (Beijing: Institute of Acoustics, Chinese Academy of Sciences
[12] 崔智强, 薛洋洋, 肖瑞, 王其乐 2021 中国水运 21 147
Cui Z Q, Xue Y Y, Xiao R, Wang Q L 2021 Chin. Water Transport 21 147
[13] 鹿力成, 马力, 陈耀明 2007 声学技术 26 787
Google Scholar
Lu L C, Ma L, Chen Y M 2007 Tech. Acoust. 26 787
Google Scholar
[14] 祝捍皓, 肖瑞, 朱军, 唐骏 2021 上海交通大学学报 55 958
Google Scholar
Zhu H H, Xiao R, Zhu J, Tang J 2021 J. Shanghai Jiao Tong Univ. 55 958
Google Scholar
[15] 邱海宾, 杨坤德 2011 兵工学报 32 298
Qiu H B, Yang K D 2011 Acta Armamentarii 32 298
[16] Kim K, Seong W, Lee K 2009 J. Acoust. Soc. Am. 125 735
Google Scholar
[17] Bonnel J, Lin Y T, Eleftherakis D, et al. 2018 J. Acoust. Soc. Am. 143 405
Google Scholar
[18] Hamilton E L, Bachman R T 1982 J. Acoust. Soc. Am. 72 1891
Google Scholar
[19] 邵宝辉 2012 硕士学位论文 (哈尔滨: 哈尔滨工程大学)
Shao B H 2012 M. S. Thesis (Harbin: Harbin Engineering University
[20] 周远晖, 陆玉昌, 石纯一 1998 清华大学学报(自然科学版) 38 93
Zhou Y H, Lu Y C, Shi C Y 1998 J. Tsinghua Univ. (Sci. & Technol. ) 38 93
[21] Bonnel J, Nicolas B, Mars J I, Walker S C 2010 J. Acoust. Soc. Am. 128 719
Google Scholar
[22] 张德明, 李整林, 张仁和 2005 声学学报 30 415
Google Scholar
Zhang D M, Li Z L, Zhang R H 2005 Acta Acustica 30 415
Google Scholar
[23] Porter M B 2001 The KRAKEN Normal Mode Program (Italy: DRAFT. SACLANT Undersea Research Center) pp1–196
[24] 牛海强, 何利, 李整林, 张仁和, 南明星 2014 声学学报 39 1
Google Scholar
Niu H Q, He L, Li Z L, Zhang R H, Nan M X 2014 Acta Acustica 39 1
Google Scholar
[25] 胡广书 1997 数字信号处理-理论、算法与实现 (北京: 清华大学出版社) 第386页
Hu G S 1997 Digital Signal Processing (Beijing: Tsinghua University Press) p386
[26] 张学磊, 李整林, 黄晓砥 2009 声学学报 34 54
Google Scholar
Zhang X L, Li Z L, Huang X D 2009 Acta Acustica 34 54
Google Scholar
[27] Zhou J X, Zhang X Z, Knobles D P 2009 J. Acoust. Soc. Am. 125 2848
Google Scholar
-
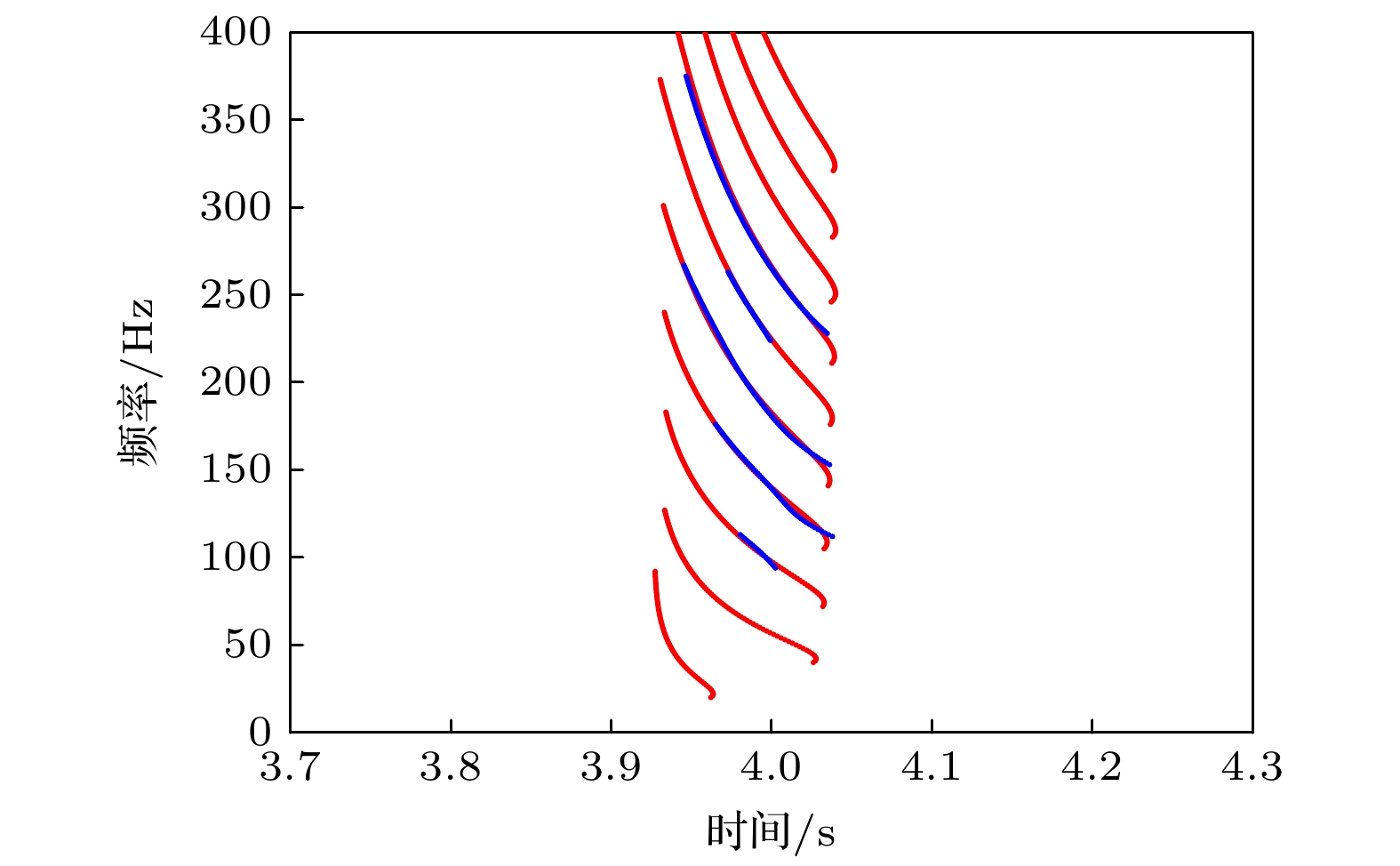
图 7 采用warping变换提取频散曲线 (a) 接收信号; (b) warping变化后的频域信号(图中红色虚线为各号简正波截止频率); (c) warping变换后信号时频图; (d) 接收信号时频图(图中白色虚线为提取出的频散曲线)
Fig. 7. Estimating dispersion curves using warping: (a) Received signal; (b) spectrum of the warped signal, and the cutoff frequency; (c) spectrogram of the warped signal; (d) spectrogram of the signal after warping and Wigner-Ville, and estimated dispersion curves.
图 8 反演参数的边缘概率密度
Fig. 8. The marginal probability distribution of inversion parameters.
图 9 频散曲线拟合图
Fig. 9. Dispersion curves as estimated from the data with warping (blue) and predicted after inversion (red).
图 11 各层声速敏感性分析
Fig. 11. One-dimension cost function value of sound speeds in each layer.
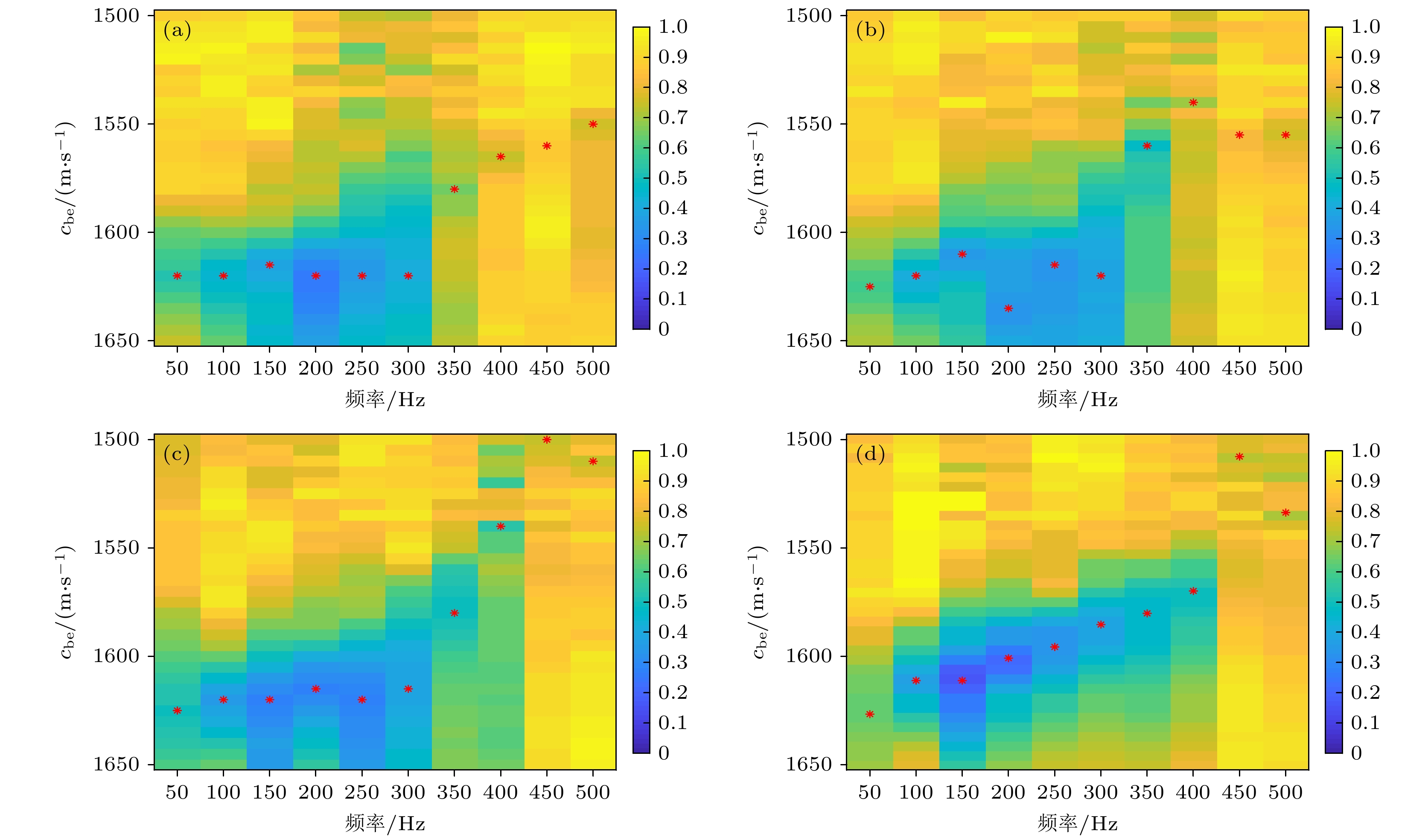
图 12 不同频率下的单层等效声速 (a) $ r = 3.5{\text{ km}} $; (b) $ r = 3.7{\text{ km}} $; (c) $ r = 3.9{\text{ km}} $; (d) $ r = 4.1{\text{ km}} $
Fig. 12. Single-layer equivalent sound speeds at different frequencies: (a) $ r = 3.5{\text{ km}} $; (b) $ r = 3.7{\text{ km}} $; (c) $ r = 3.9{\text{ km}} $; (d) $ r = 4.1{\text{ km}} $.
图 14 不同频率的传播损失 (a) 225 Hz; (b) 375 Hz
Fig. 14. Comparison of theoretical and experimental transmission-loss at different frequencies: (a) 225 Hz; (b) 375 Hz.
表 1 不同距离下海底参数反演结果
Table 1. Inversion results at different distances.
反演参数 符号 单位 样本1 样本2 样本3 样本4 样本5 收发距离 $r$ ${\mathrm{ km}} $ 5.3 5.8 6 7.8 9.3 第一层海底声速 ${c_{{\text{b}}1}}$ ${\mathrm{m/s}}$ 1640 1614 1631 1613 1600 第二层海底声速 ${c_{{\text{b}}2}}$ ${\mathrm{m/s}}$ 1566 1576 1576 1570 1578 第三层海底声速 ${c_{{\text{b}}3}}$ ${\mathrm{m/s}}$ 1610 1624 1636 1613 1603 第一层海底平均厚度 ${h_1}$ $ {\mathrm{m}} $ 8.82 8.68 8.71 8.55 8.29 第一层海底密度 ${\rho _1}$ ${\text{g}}/{\mathrm{c}}{{\mathrm{m}}^3}$ 1.79 1.73 1.76 1.73 1.69 第二层平均海底厚度 ${h_2}$ $ {\mathrm{m}} $ 9.07 9.13 8.92 8.78 8.83 第二层海底密度 ${\rho _2}$ ${\text{g}}/{\mathrm{c}}{{\mathrm{m}}^3}$ 1.60 1.63 1.62 1.61 1.63 第三层海底平均厚度 ${h_3}$ $ {\mathrm{m}} $ 32.46 32.78 32.22 30.97 29.77 第三层海底密度 ${\rho _3}$ ${\text{g}}/{\mathrm{c}}{{\mathrm{m}}^3}$ 1.72 1.75 1.78 1.72 1.70 
下载: 导出CSV
表 2 仿真中不同频率下反演获取的单层等效声速
Table 2. Single-layer equivalent sound speeds at different frequencies.
频率/${\text{Hz}}$ 50 100 150 200 250 300 350 400 450 500 声速/(m·s–1) 1725 1625 1605 1595 1590 1585 1585 1585 1580 1585 代价函数 0.36 0.57 0.54 0.30 0.31 0.21 0.14 0.10 0.12 0.15
下载: 导出CSV
表 3 在100—150 Hz频段表层参数的反演结果
Table 3. Inversion results of the surface layer at 100—150 Hz.
距离/km $ {c_{{\text{b}}11}} $/(m·s–1) $ {c_{{\text{b}}12}} $/(m·s–1) $ {c_{{\text{ba}}}} $/(m·s–1) $ {h_{11}} $/m $ {c_{{\text{b}}13}} $/(m·s–1) $ {h_{12}} $/m 3.7 1540 1585 1562.5 4.18 1665 4.55 4.1 1535 1599 1567 4.24 1665 4.49 4.3 1566 1604 1585 4.28 1672 4.51 4.8 1568 1598 1583 4.31 1670 4.45 5.5 1568 1597 1582.5 4.33 1669 4.37 6 1565 1592 1578.5 4.32 1657 4.35
下载: 导出CSV
表 4 5 km站位采样样品分析结果
Table 4. Sample results at 5 km site.
土样编号 层位 温度 水深 声速 密度(湿) 名称 D/cm T/℃ Z/m c/(m·s–1) ρ/(g·cm–3) S63511-1 0—40 20.5 83 1542.93 1.66 粘土质粉砂 S63512-1 40—80 20.5 83 1558.55 1.66 粘土质粉砂 S63513-1 80—120 20.5 83 1528.57 1.69 粘土质粉砂 S63514-1 120—150 20.5 83 1539.44 1.75 砂质粉砂 S63521-1 150—190 21.0 83 1564.67 1.82 粘土质粉砂 S63522-1 190—230 21.0 83 1517.44 1.77 粘土质粉砂 S63523-1 230—270 21.0 83 1588.24 1.77 粘土质粉砂 S63524-1 230—300 21.0 83 1564.69 1.77 粘土质粉砂 S63531-1 300—330 21.0 83 1565.55 1.90 砂质粉砂 S63532-1 330—360 21.0 83 1616.20 1.92 粉砂质砂 S63533-1 360—400 21.0 83 1568.53 1.98 粉砂质砂 平均 1560
下载: 导出CSV
表 5 不同频率下反演的衰减系数及反演结果预报声传播损失的平均误差
Table 5. The inversion result of attenuation coefficient and their errors.
频率/Hz 100 150 200 225 300 325 375 400 450 475 $ \alpha /({\mathrm{dB}} {\cdot} {{\mathrm{m}}^{ - 1}}) $ 0.001 0.007 0.015 0.022 0.033 0.04 0.045 0.061 0.078 0.094 误差$ /{\mathrm{dB}} $ 2.91 1.70 1.68 1.42 1.61 1.78 2.27 2.23 2.37 2.60
下载: 导出CSV
表 6 单层海底模型下反演结果
Table 6. Inversion results for single-layer bottom model.
频率/Hz 100 150 200 225 300 ${c_{\text{e}}}/({\text{m}} {\cdot }{{\text{s}}^{{{ - }}1}})$ 1615 1615 1615 1613 1600 $ \alpha /({\mathrm{dB}}{ \cdot} {{\mathrm{m}}^{ - 1}}) $ 0.0001 0.011 0.022 0.032 0.04 误差$ /{\mathrm{dB}} $ 3.98 1.81 1.71 1.53 1.68
下载: 导出CSV
-
[1] Taroudakis M I, Markaki M G 1998 J. Comput. Acoust. 6 167
Google Scholar
[2] 杨坤德 2003 博士学位论文 (西安: 西北工业大学)
Yang K D 2003 Ph. D. Dissertation (Xi’an: Northwestern Polytechnical University
[3] Cobo P P, Ranz G C 1989 J. Acoust. Soc. Am. 85 2388
Google Scholar
[4] Zhou J X 1985 J. Acoust. Soc. Am. 78 1003
Google Scholar
[5] 赵梅, 胡长青 2009 声学技术 28 104
Google Scholar
Zhao M, Hu C Q 2009 Tech. Acoust. 28 104
Google Scholar
[6] 李风华, 张仁和 2000 声学学报 25 297
Google Scholar
Li F H, Zhang R H 2000 Acta Acustica 25 297
Google Scholar
[7] Yang T C, Yoo K, Fialkowski L T 2007 J. Acoust. Soc. Am. 122 3338
Google Scholar
[8] 翁晋宝, 李风华, 郭永刚 2015 声学学报 40 207
Google Scholar
Weng J B, Li F H, Guo Y G 2015 Acta Acustica 40 207
Google Scholar
[9] Li Z L, Zhang R H 2004 Chin. Phys. Lett. 21 1100
Google Scholar
[10] 李梦竹, 李整林, 周纪浔, 张仁和 2019 68 094301
Google Scholar
Li M Z, Li Z L, Zhou J X, Zhang R H 2019 Acta Phys. Sin. 68 094301
Google Scholar
[11] 吴双林 2016 硕士学位论文 (北京: 中国科学院声学研究所)
Wu S L 2016 M. S. Thesis (Beijing: Institute of Acoustics, Chinese Academy of Sciences
[12] 崔智强, 薛洋洋, 肖瑞, 王其乐 2021 中国水运 21 147
Cui Z Q, Xue Y Y, Xiao R, Wang Q L 2021 Chin. Water Transport 21 147
[13] 鹿力成, 马力, 陈耀明 2007 声学技术 26 787
Google Scholar
Lu L C, Ma L, Chen Y M 2007 Tech. Acoust. 26 787
Google Scholar
[14] 祝捍皓, 肖瑞, 朱军, 唐骏 2021 上海交通大学学报 55 958
Google Scholar
Zhu H H, Xiao R, Zhu J, Tang J 2021 J. Shanghai Jiao Tong Univ. 55 958
Google Scholar
[15] 邱海宾, 杨坤德 2011 兵工学报 32 298
Qiu H B, Yang K D 2011 Acta Armamentarii 32 298
[16] Kim K, Seong W, Lee K 2009 J. Acoust. Soc. Am. 125 735
Google Scholar
[17] Bonnel J, Lin Y T, Eleftherakis D, et al. 2018 J. Acoust. Soc. Am. 143 405
Google Scholar
[18] Hamilton E L, Bachman R T 1982 J. Acoust. Soc. Am. 72 1891
Google Scholar
[19] 邵宝辉 2012 硕士学位论文 (哈尔滨: 哈尔滨工程大学)
Shao B H 2012 M. S. Thesis (Harbin: Harbin Engineering University
[20] 周远晖, 陆玉昌, 石纯一 1998 清华大学学报(自然科学版) 38 93
Zhou Y H, Lu Y C, Shi C Y 1998 J. Tsinghua Univ. (Sci. & Technol. ) 38 93
[21] Bonnel J, Nicolas B, Mars J I, Walker S C 2010 J. Acoust. Soc. Am. 128 719
Google Scholar
[22] 张德明, 李整林, 张仁和 2005 声学学报 30 415
Google Scholar
Zhang D M, Li Z L, Zhang R H 2005 Acta Acustica 30 415
Google Scholar
[23] Porter M B 2001 The KRAKEN Normal Mode Program (Italy: DRAFT. SACLANT Undersea Research Center) pp1–196
[24] 牛海强, 何利, 李整林, 张仁和, 南明星 2014 声学学报 39 1
Google Scholar
Niu H Q, He L, Li Z L, Zhang R H, Nan M X 2014 Acta Acustica 39 1
Google Scholar
[25] 胡广书 1997 数字信号处理-理论、算法与实现 (北京: 清华大学出版社) 第386页
Hu G S 1997 Digital Signal Processing (Beijing: Tsinghua University Press) p386
[26] 张学磊, 李整林, 黄晓砥 2009 声学学报 34 54
Google Scholar
Zhang X L, Li Z L, Huang X D 2009 Acta Acustica 34 54
Google Scholar
[27] Zhou J X, Zhang X Z, Knobles D P 2009 J. Acoust. Soc. Am. 125 2848
Google Scholar
下载:
计量
- 文章访问数: 2027
- PDF下载量: 103
- 被引次数: 0
