-
火星声探测技术逐渐成为火星探测的一种重要手段. 为了探测火星声源, 需研究稀薄低温火星大气中的声速和声衰减、建立分层大气中的声传播模型. 本文提出了一种结合Navier-Stokes (NS)声波方程和变组分混合气体的声速模型, 考虑了火星极端稀薄大气中的声频散, 将火星声速剖面模拟计算拓展到0—250 km海拔范围, 并讨论了NS声速剖面的适用条件. 本文实验验证了低压、低温环境中, 在分子平动、旋转和振动弛豫作用下, 三原子二氧化碳中存在明显声频散. 随后分别基于频散NS声速和无频散理想气体声速剖面, 模拟了地面声源和高空声源产生的不同频率声波的传播路径. 研究发现声频散显著影响了声传播路径, 降低了声线首次折返高度、缩短了声线折回火星地表的距离、减小了第一声影区的范围等. 而且频率越高、声源海拔高度越高, 频散对声传播的影响越剧烈, NS方程的连续性假设失效, 更高频的声波需要基于Boltzmann方程和分子模拟法建立声频散模型.At present, Mars acoustic detection is gradually becoming an important new tool for understanding and exploring Mars. To explore the sources of Mars sound, it is necessary to study the sound speed and the sound attenuation in the thin and low-temperature Martian atmosphere, and to model the sound propagation in the stratified atmosphere. According to the extremely low pressure of Mars and the large variation of gas composition with altitude, we propose a simulation method based on the Navier-Stokes (NS) equation and the mixed-gas model to calculate the vertical profiles of sound speed and attenuation in the Martian atmosphere at 0–250 km altitude in this work. A comparison among sound-speed profiles at different frequencies shows that there is a notable sound dispersion in the Martian atmosphere, especially at high altitudes and in the high frequency range. It is also verified through sound speed measurement experiments that significant sound dispersion does exist in low-pressure carbon dioxide, implying the need to consider sound dispersion in the modelling of Martian sound speed profiles. The scope of application of the NS equation in modelling the sound speed of the Martian atmosphere is also discussed, as the NS equation may fail in a too rarefied gas. Next, the non-dispersive ideal-gas sound speed profiles and the dispersive NS sound speed at different frequencies (0.01, 0.1, 1 Hz) are used to simulate the sound propagation paths in the multilayered Martian atmosphere. And both cases of the Martian ground-based and high-altitude sources are compared with each other. It is found that the dispersive sound speed has a significant effect on the sound propagation path on Mars. The main influence is that the first fold back height and the first return distance of the sound ray to the surface are both shortened, which directly changes the area and location of the acoustic quiet zone. The effect of dispersion on the sound propagation path becomes more notable with both the frequency and the elevation of the acoustic source increasing, confirming that consideration of dispersion has a significant effect on the calculation of the sound propagation path.
-
Keywords:
- Mars acoustic detection /
- acoustic dispersion /
- mixed-gas sound speed /
- rarefied gas
[1] Maurice S, Chide B, Murdoch N, Lorenz R D, Mimoun D, Wiens R C, Stott A, Jacob X, Bertrand T, Montmessin F, Lanza N L, Alvarez-Llamas C, Angel S M, Aung M, Balaram J, Beyssac O, Cousin A, Delory G, Forni O, Fouchet T, Gasnault O, Grip H, Hecht M, Hoffman J, Laserna J, Lasue J, Maki J, McClean J, Meslin P Y, Le Mouélic S, Munguira A, Newman C E, Rodríguez Manfredi J A, Moros J, Ollila A, Pilleri P, Schröder S, de la Torre Juárez M, Tzanetos T, Stack K M, Farley K, Williford K, the SuperCam team 2022 Nature 605 653
Google Scholar
[2] Peng Y, Zhang L, Cai Z, Wang Z, Jiao H, Wang D, Li Y 2020 Earth Planet. Phys. 4 371
Google Scholar
[3] Christie R, Campus P 2010 Infrasound Monitoring for Atmospheric Studies (Dordrecht: Springer Science and Business Media) pp541–574
[4] Lamb D, Lees J M, Bowman D C 2018 Geophys. Res. Lett. 45 7176
Google Scholar
[5] 毕思昭, 彭朝晖 2021 70 114303
Google Scholar
Bi S Z, Peng Z H 2021 Acta Phys. Sin. 70 114303
Google Scholar
[6] 程巍, 滕鹏晓, 吕君, 姬培锋, 戴翊靖 2021 70 244203
Google Scholar
Cheng W, Teng P X, Lü J, Ji P F, Dai Y J 2021 Acta Phys. Sin. 70 244203
Google Scholar
[7] 苏林, 马力, 宋文华, 郭圣明, 鹿力成 2015 64 024302
Google Scholar
Su L, Ma L, Song W H, Guo S M, Lu L C 2015 Acta Phys. Sin. 64 024302
Google Scholar
[8] Williams J P 2001 J. Geophys. Res. Planets 106 5033
Google Scholar
[9] Kalempa D, Sharipov F 2009 Phys. Fluids 21 103601
Google Scholar
[10] Rayleigh J W S B 1896 The Theory of Sound (Vol. 2) (London: Macmillan) pp344–352
[11] Chang W, Uhlenbeck G E 1948 Studies Statistical Mech. 5 1
[12] Chang W, Uhlenbeck G E 1948 Studies Statistical Mech. 5 17
[13] Sirovich L, Thurber J K 1965 J. Acoust. Soc. Am. 37 329
Google Scholar
[14] Greenspan M 1950 J. Acoust. Soc. Am. 22 568
Google Scholar
[15] Greenspan M 1954 J. Acoust. Soc. Am. 26 70
Google Scholar
[16] Greenspan M 1956 J. Acoust. Soc. Am. 28 644
Google Scholar
[17] Greenspan M 1959 J. Acoust. Soc. Am. 31 155
Google Scholar
[18] Bird G A 1994 Molecular Gas Dynamics and the Direct Simulation of Gas Flows (USA: Oxford University Press) pp1–29
[19] Cercignani C 1988 The Boltzmann Equation and its Application (New York: SpringerVerlag) pp351–385
[20] Sharipov F 2016 Rarefied Gas Dynamics. Fundamentals for Research and Practice (Berlin: Wiley-VCH) pp73–81
[21] Hadjiconstantinou N G, Garcia A L 2001 Phys. Fluids 13 1040
Google Scholar
[22] Hanford A D 2008 Ph. D. Dissertation (Pennsylvania: The Pennsylvania State University)
[23] Kalempa D, Sharipov F 2016 Eur. J. Mech. B-Fluid 57 50
Google Scholar
[24] Kalempa D, Sharipov F, Silva J C 2019 Vacuum 159 82
Google Scholar
[25] Meyer E, Sessler G 1957 Z. Phys. 149 15
Google Scholar
[26] Maidanik G, Heckl M 1965 Phys. Fluids 8 266
Google Scholar
[27] Hirschfelder J O, Curtiss C F, Bird R B 1964 Molecular Theory of Gases and Liquids (New York: John Wiley & Sons, Inc) pp533–543
[28] Mason W P 1984 Physical Acoustics : Principles and Methods (Vol. 17) (New York: Academic Press) pp145–228
[29] Sutherland L C, Bass H E 2004 J. Acoust. Soc. Am. 115 1012
Google Scholar
[30] Bass H E, Chambers J P 2001 J. Acoust. Soc. Am. 109 3069
Google Scholar
[31] Petculescu A, Achi P 2012 J. Acoust. Soc. Am. 131 3671
Google Scholar
[32] Petculescu A 2016 J. Acoust. Soc. Am. 140 1439
Google Scholar
[33] Trahan A J, Petculescu A 2020 J. Acoust. Soc. Am. 148 141
Google Scholar
[34] Forget F, Hourdin F, Fournier R, Hourdin C, Talagrand O, Collins M, Huot J P 1999 J. Geophys. Res. Planets 104 24155
Google Scholar
[35] Millour E, Forget F, Spiga A, Vals M, Zakharov V, Montabone L 2018 Icarus From Mars Express to ExoMars 150 27
[36] Chase M W, National Information Standards Organization (US) 1998 NIST-JANAF Thermochemical Tables (Vol. 9) (Washington, DC: American Chemical Society) pp1–1951
[37] Greenspan M 1987 J. Acoust. Soc. Am. 82 370
Google Scholar
[38] Greenspan M 1965 Physical Acoustics, 2 (Part A) (New York: Academic Press) pp1–43
[39] Bird R B 2002 Appl. Mech. Rev. 55 R1
Google Scholar
[40] Hirschfelder J O, Bird R B, Spotz E L 1948 J. Chem. Phys. 16 968
Google Scholar
[41] 杨训仁, 陈宇 2007 大气声学 (北京: 科学出版社) 第52—59页
Yang X R, Chen Y 2007 Atmospheric Acoustic (Beijing: Science Press) pp52–59 (in Chinese)
[42] White R D, Neeson I, Schmid E S, Merrison J, Iversen J J, Banfield D 2020 AIAA Scitech 2020 Forum Orlando, Florida, USA, January 6–10, 2020 p0712
-
图 1 不同海拔下火星的大气参数 (a)气体成分; (b)温度; (c)气压; (d)水平风速
Fig. 1. Atmospheric parameters of Mars at different altitudes: (a) Gas composition; (b) temperature; (c) pressure; (d) horizontal wind speed
图 2 火星大气(a)分子摩尔质量、(b)比热比和(c)理想气体声速的垂直剖面图
Fig. 2. Vertical profiles of (a) the molecular molar mass, (b) specific heat ratio, and (c) ideal gas sound speed of the Martian atmosphere
图 3 火星大气中6种主要气体成分的定压热容随温度的变化
Fig. 3. Variation of the constant pressure heat capacity of the six main gas components of the Martian atmosphere with temperature
图 4 时差法测量声速实验装置图 (a)示意图; (b)实物图
Fig. 4. Diagram of the experimental setup for measuring sound speed by the time difference method: (a) Schematic diagram; (b) physical diagram
图 5 二氧化碳中21 kHz 声波速度随气压的变化 (a) 0 ℃左右; (b) –20 ℃左右
Fig. 5. Variation of sound speed of 21 kHz sound wave with pressure in carbon dioxide: (a) Around 0 ℃; (b) around –20 ℃
图 6 火星大气6种主要气体成分在100—300 K温度范围内的黏温曲线
Fig. 6. Viscosity-temperature curves of the six main gas components of the Martian atmosphere in the temperature range of 100–300 K
图 7 不同海拔下火星多组分混合大气中的(a)黏度、(b)热导率和(c)无量纲数P的垂直剖面图
Fig. 7. Vertical profiles of (a) viscosity, (b) thermal conductivity, and (c) dimensionless number P in the multi-component mixed atmosphere of Mars at different altitudes
图 8 不同海拔下、不同频率的声波在火星大气中的NS方程声速剖面, 其中虚线代表NS声速不适用的海拔范围
Fig. 8. NS equation sound speed profiles in the Martian atmosphere for sound waves at different altitudes and frequencies, where the dashed line represents the altitude range where the NS sound velocity does not apply
图 9 火星大气中0.01 Hz声波的声吸收系数随海拔的变化
Fig. 9. Variation of the acoustic absorption coefficient with altitude for 0.01 Hz sound waves in the Martian atmosphere
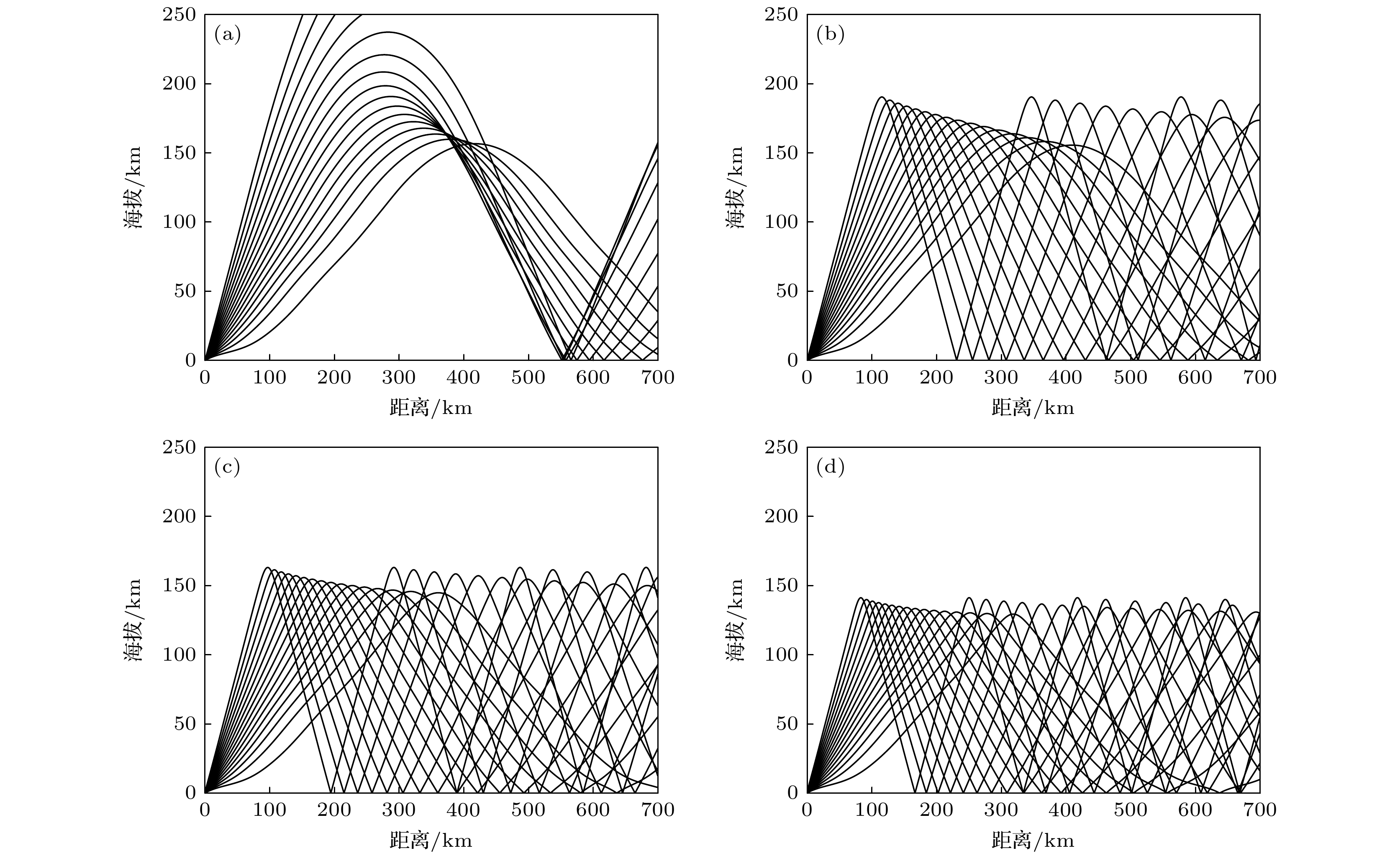
图 10 火星不同声速剖面模型下声传播路径预测 (a)理想气体声速; (b) 0.01 Hz, (c) 0.1 Hz和(d) 1 Hz的声波NS声速, 其中不同曲线表示声线向不同角度发射, 射线发射角度范围15°—60°, 角度间隔3°, 水平范围0—700 km
Fig. 10. Predicted sound propagation paths for different sound speed profile models of Mars: (a) Ideal gas sound speed; (b) 0.01 Hz, (c) 0.1 Hz and (d) 1 Hz NS sound speed, where different curves indicate sound lines emitted at different angles, with ray emission angles range from 15° to 60°, angular interval 3°, horizontal range 0–700 km
图 11 声源高度对声传播路径的影响. 基于理想气体声速剖面的 (a) 50 km, (c) 110 km, (e) 150 km高度声源的传播路径; 基于0.01 Hz声波的NS声速剖面模拟的(b) 50 km, (d) 110 km, (f) 150 km高度声源的传播路径; 其中不同曲线表示声线向不同角度发射, 射线的发射角度–45°—45°, 角度间隔3°, 水平范围0—700 km
Fig. 11. Effect of sound source height on sound propagation paths. Propagation paths of sources at (a) 50 km, (c) 110 km, and (e) 150 km based on ideal gas sound speed profiles; propagation paths of sources at (b) 50 km, (d) 110 km, and (f) 150 km based on simulated NS sound speed profiles of 0.01 Hz sound waves; where different curves indicate sound lines emitted at different angles, with ray emission angles range from –45° to 45°, angular interval 3°, horizontal range 0–700 km
表 1 不同气体的分子摩尔质量
Table 1. Molar masses of molecules of different gases
气体种类 分子摩尔质量Mi /(g·mol–1) CO2 44.0095 N2 28.0134 Ar 39.9480 CO 28.0101 O 15.9994 H2 2.01588 
下载: 导出CSV
表 2 火星主要气体成分Shomate公式系数
Table 2. Shomate formula coefficients for the major gas constituents of Mars
气体 A B C D E CO2 24.9974 55.1870 –33.6914 7.94839 –0.136638 Ar 20.7860 2.82591 × 10–7 –1.46419 × 10–7 1.09213 × 10–8 –3.66137 × 10–8 N2 28.9864 1.85398 –9.64746 16.6354 0.000117 CO 25.5676 6.09613 4.05466 –2.67130 0.131021 O — — — — — H2 33.0662 –11.3634 11.4328 –2.7728 –0.15856
下载: 导出CSV
表 3 火星大气中不同频率声波NS声速适用失效海拔范围
Table 3. Applicable failure altitude range of the NS sound speed for different frequencies of acoustic waves in the Martian atmosphere
频率/Hz 0.01 0.1 1 NS声速适用高度/km < 250.0 < 188.0 < 149.9
下载: 导出CSV
表 4 不同声速剖面下的声线对比
Table 4. Comparison of sound lines at different sound velocity profiles
理想气体声速 0.01 Hz NS声速 0.1 Hz NS声速 1 Hz NS声速 折回高度/km 237.3 190.5 163.2 141.3 声影区/km 554.3 231.2 194.9 167.3
下载: 导出CSV
-
[1] Maurice S, Chide B, Murdoch N, Lorenz R D, Mimoun D, Wiens R C, Stott A, Jacob X, Bertrand T, Montmessin F, Lanza N L, Alvarez-Llamas C, Angel S M, Aung M, Balaram J, Beyssac O, Cousin A, Delory G, Forni O, Fouchet T, Gasnault O, Grip H, Hecht M, Hoffman J, Laserna J, Lasue J, Maki J, McClean J, Meslin P Y, Le Mouélic S, Munguira A, Newman C E, Rodríguez Manfredi J A, Moros J, Ollila A, Pilleri P, Schröder S, de la Torre Juárez M, Tzanetos T, Stack K M, Farley K, Williford K, the SuperCam team 2022 Nature 605 653
Google Scholar
[2] Peng Y, Zhang L, Cai Z, Wang Z, Jiao H, Wang D, Li Y 2020 Earth Planet. Phys. 4 371
Google Scholar
[3] Christie R, Campus P 2010 Infrasound Monitoring for Atmospheric Studies (Dordrecht: Springer Science and Business Media) pp541–574
[4] Lamb D, Lees J M, Bowman D C 2018 Geophys. Res. Lett. 45 7176
Google Scholar
[5] 毕思昭, 彭朝晖 2021 70 114303
Google Scholar
Bi S Z, Peng Z H 2021 Acta Phys. Sin. 70 114303
Google Scholar
[6] 程巍, 滕鹏晓, 吕君, 姬培锋, 戴翊靖 2021 70 244203
Google Scholar
Cheng W, Teng P X, Lü J, Ji P F, Dai Y J 2021 Acta Phys. Sin. 70 244203
Google Scholar
[7] 苏林, 马力, 宋文华, 郭圣明, 鹿力成 2015 64 024302
Google Scholar
Su L, Ma L, Song W H, Guo S M, Lu L C 2015 Acta Phys. Sin. 64 024302
Google Scholar
[8] Williams J P 2001 J. Geophys. Res. Planets 106 5033
Google Scholar
[9] Kalempa D, Sharipov F 2009 Phys. Fluids 21 103601
Google Scholar
[10] Rayleigh J W S B 1896 The Theory of Sound (Vol. 2) (London: Macmillan) pp344–352
[11] Chang W, Uhlenbeck G E 1948 Studies Statistical Mech. 5 1
[12] Chang W, Uhlenbeck G E 1948 Studies Statistical Mech. 5 17
[13] Sirovich L, Thurber J K 1965 J. Acoust. Soc. Am. 37 329
Google Scholar
[14] Greenspan M 1950 J. Acoust. Soc. Am. 22 568
Google Scholar
[15] Greenspan M 1954 J. Acoust. Soc. Am. 26 70
Google Scholar
[16] Greenspan M 1956 J. Acoust. Soc. Am. 28 644
Google Scholar
[17] Greenspan M 1959 J. Acoust. Soc. Am. 31 155
Google Scholar
[18] Bird G A 1994 Molecular Gas Dynamics and the Direct Simulation of Gas Flows (USA: Oxford University Press) pp1–29
[19] Cercignani C 1988 The Boltzmann Equation and its Application (New York: SpringerVerlag) pp351–385
[20] Sharipov F 2016 Rarefied Gas Dynamics. Fundamentals for Research and Practice (Berlin: Wiley-VCH) pp73–81
[21] Hadjiconstantinou N G, Garcia A L 2001 Phys. Fluids 13 1040
Google Scholar
[22] Hanford A D 2008 Ph. D. Dissertation (Pennsylvania: The Pennsylvania State University)
[23] Kalempa D, Sharipov F 2016 Eur. J. Mech. B-Fluid 57 50
Google Scholar
[24] Kalempa D, Sharipov F, Silva J C 2019 Vacuum 159 82
Google Scholar
[25] Meyer E, Sessler G 1957 Z. Phys. 149 15
Google Scholar
[26] Maidanik G, Heckl M 1965 Phys. Fluids 8 266
Google Scholar
[27] Hirschfelder J O, Curtiss C F, Bird R B 1964 Molecular Theory of Gases and Liquids (New York: John Wiley & Sons, Inc) pp533–543
[28] Mason W P 1984 Physical Acoustics : Principles and Methods (Vol. 17) (New York: Academic Press) pp145–228
[29] Sutherland L C, Bass H E 2004 J. Acoust. Soc. Am. 115 1012
Google Scholar
[30] Bass H E, Chambers J P 2001 J. Acoust. Soc. Am. 109 3069
Google Scholar
[31] Petculescu A, Achi P 2012 J. Acoust. Soc. Am. 131 3671
Google Scholar
[32] Petculescu A 2016 J. Acoust. Soc. Am. 140 1439
Google Scholar
[33] Trahan A J, Petculescu A 2020 J. Acoust. Soc. Am. 148 141
Google Scholar
[34] Forget F, Hourdin F, Fournier R, Hourdin C, Talagrand O, Collins M, Huot J P 1999 J. Geophys. Res. Planets 104 24155
Google Scholar
[35] Millour E, Forget F, Spiga A, Vals M, Zakharov V, Montabone L 2018 Icarus From Mars Express to ExoMars 150 27
[36] Chase M W, National Information Standards Organization (US) 1998 NIST-JANAF Thermochemical Tables (Vol. 9) (Washington, DC: American Chemical Society) pp1–1951
[37] Greenspan M 1987 J. Acoust. Soc. Am. 82 370
Google Scholar
[38] Greenspan M 1965 Physical Acoustics, 2 (Part A) (New York: Academic Press) pp1–43
[39] Bird R B 2002 Appl. Mech. Rev. 55 R1
Google Scholar
[40] Hirschfelder J O, Bird R B, Spotz E L 1948 J. Chem. Phys. 16 968
Google Scholar
[41] 杨训仁, 陈宇 2007 大气声学 (北京: 科学出版社) 第52—59页
Yang X R, Chen Y 2007 Atmospheric Acoustic (Beijing: Science Press) pp52–59 (in Chinese)
[42] White R D, Neeson I, Schmid E S, Merrison J, Iversen J J, Banfield D 2020 AIAA Scitech 2020 Forum Orlando, Florida, USA, January 6–10, 2020 p0712
下载:
计量
- 文章访问数: 4607
- PDF下载量: 63
- 被引次数: 0
