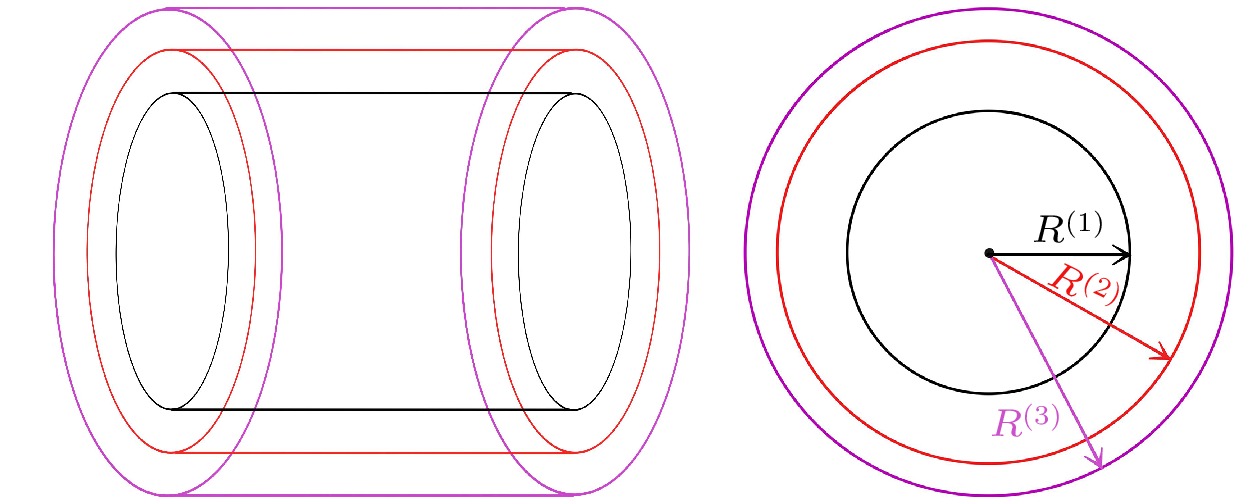
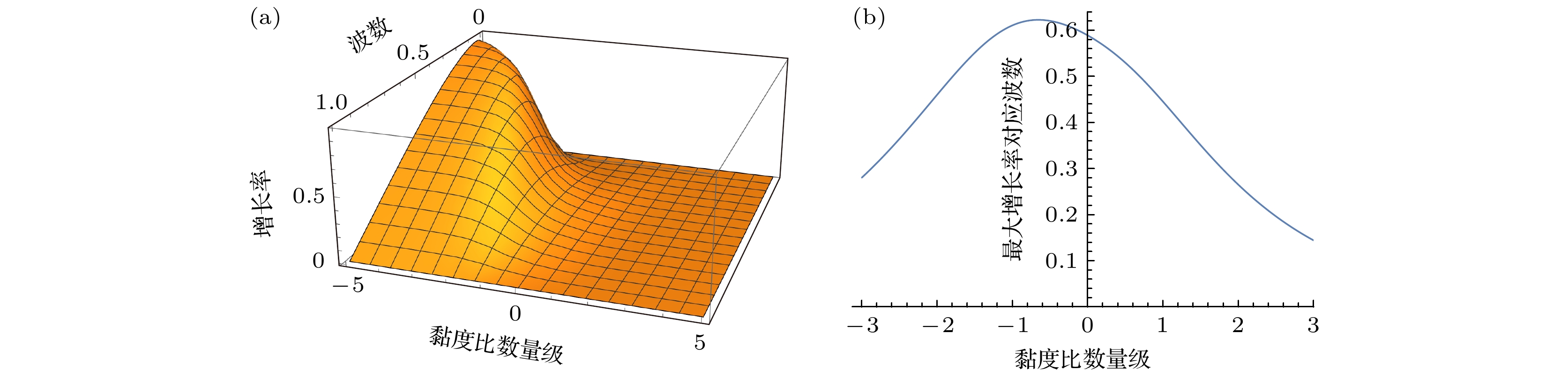
-
由于马兰戈尼效应, 液滴在液体层表面自发铺展成薄膜的物理过程, 在成膜技术、涂层工艺、以及纳米器件的制作等领域具有广泛的应用, 但是铺展后液膜自发碎裂成小液滴的现象也被广泛观察到, 这种现象限制了马兰戈尼效应应用的发展. 本文基于以往的实验观察对液膜的碎裂机制进行完备的解释, 并通过实验进行验证, 指出了液滴薄膜中心与边缘蒸发速率的差异引起的马兰戈尼流动对液膜边界产生的微扰, 使得液滴铺展到最大时边缘生长出指状液柱. 此外, 根据微扰模型推导出边界失稳的临界波长和最大波长的表达式, 基于Plateau-Rayleigh不稳定性解释了指状液柱碎裂的原因. 建立同心圆柱壳液柱模型简化计算, 预测了不同黏度比的液滴在液体层上铺展为薄膜的浓度范围和发生马兰戈尼爆裂的位置区间, 并通过实验验证了不同醇溶液发生马兰戈尼爆裂的浓度范围和位置区间. 该理论解释将在成膜技术、涂层工艺等领域提供更加精细的理论指导; 特别地, 本文提出的同心圆柱壳简化模型为化工领域微量反应和纳米颗粒制备等研究领域中的一些技术难题提供新的解决思路.
-
关键词:
- 铺展系数 /
- 马兰戈尼效应 /
- 边界失稳 /
- Plateau-Rayleigh不稳定性
In this work, the process of forming micro-droplets due to instability and fragmentation after short chain alcohol solution spreads on the surface of oil layers is studied. Based on the free energy theory of the liquid-liquid interface, the relationship between the binary mixtures spreading on the surface of the liquid layer is derived, and the concentration range of short chain alcohol solution spreading as a thin film on the surface of the oil layer is calculated from the Hiskovsky formula. The Malangoni flow caused by the difference in evaporation rate between the center and edge of the droplet film perturbs the boundary of the liquid film, causing finger-shaped liquid columns to grow at the edge when the droplet spreads to its maximum. In this work, the expression for the critical wavelength and maximum wavelength of boundary instability are derived based on the perturbation model, and the reason for finger shaped liquid column fragmentation is explained based on the Plateau Rayleigh instability. A concentric cylindrical shell liquid column model is established to simplify the calculation and predict the location range of “droplet explosion” of droplets with different viscosity ratios on the liquid layer. Through theoretical calculations and experimental verification, it is found that the alcohol solution fragmented into small droplets within a length range of 4.51–5.98 times the width of the liquid column. This study provides theoretical guidance for existing application fields such as film forming technology and coating technology. The hypotheses, assumptions, and simplified models preliminarily verified experimentally provide solutions for some technical difficulties in the research fields of micro reactions and nanoparticle preparation in chemical industry.-
Keywords:
- spread coefficient /
- Marangoni burst /
- boundary instability /
- Plateau-Rayleigh instability
[1] Zhang J, Oron A, Behringer R P 2011 Phys. Fluids 23 072102
Google Scholar
[2] 赵子强, 韦伦存, 王浩, 张金宏, 钟运成, 卢希庭 1997 46 878
Google Scholar
Zhao Z Q, Wei L C, Wang H, Zhang J H, Zhong Y C, Lu X T 1997 Acta Phys. Sin. 46 878
Google Scholar
[3] 马书鹏, 林飞宇, 罗媛, 朱刘, 郭学益, 杨英 2022 71 158101
Google Scholar
Ma S P, Lin F Y, Luo Y, Zhu L, Guo X Y, Yang Y 2022 Acta Phys. Sin. 71 158101
Google Scholar
[4] Fay J A 1969 Oil on the Sea (Boston: Springer) pp53–63
[5] Huh C, Inoue M, Mason S G 1975 Can. J. Chem. Eng. 53 367
Google Scholar
[6] Foda M, Cox R G 1980 J. Fluid Mech. 101 33
Google Scholar
[7] Chaudhary K C, Redeopp L G 1980 Theory. J. Fluid Mech. 96 257
Google Scholar
[8] Chaudhary K C, Maxworthy T 1980 J. Fluid Mech. 96 275
Google Scholar
[9] Smith M K, Davis S H 1983 J. Fluid Mech. 132 119
Google Scholar
[10] Smith M K, Davis S H 1983 J. Fluid Mech. 132 145
Google Scholar
[11] Fanton X, Cazabat A M 1998 Langmuir 14 2554
Google Scholar
[12] Dussaud A D, Trojan S T 1998 Phys. Fluids 10 23
Google Scholar
[13] Borgas M S, Grotberg J B 1988 J. Fluid Mech. 188 151
Google Scholar
[14] Santiago Rosanne M, Vignes Adler M, Velarde M G 1997 J. Colloid. Interface Sci. 191 651
Google Scholar
[15] Vuilleumier R, Ego V, Neltner L, Cazabat A M 1995 Langmuir 11 4117
Google Scholar
[16] Kataoka D E, Troian S M 1997 J. Colloid. Nterf. Sci. 192 350
Google Scholar
[17] Jensen O E 1995 J. Fluid Mech. 293 349
Google Scholar
[18] Berg S 2009 Phys. Fluids 21 032105
Google Scholar
[19] Yamamoto D, Nakajima C, Shioi A, Krafft M P, Yoshikawa K 2015 Nat. Commun. 6 7189
Google Scholar
[20] Eggers J, Villermaux E 2008 Rep. Prog. Phys. 71 036601
Google Scholar
[21] Keiser L, Bense H, Colinet P, Bico J, Reyssat E 2017 Phys. Rev. Lett. 118 074504
Google Scholar
[22] Hamraoui A, Cachile M, Poulard C, Cazabat A M 2004 Colloid Surf. A Physicochem. Eng. Asp. 250 215
Google Scholar
[23] Hernández-Sánchez J F, Eddi A, Snoeijer J H 2015 Phys. Fluids 27 032003
Google Scholar
[24] 赵文景, 王进, 秦威广, 纪文杰, 蓝鼎, 王育人 2021 70 184701
Google Scholar
Zhao W J, Wang J, Qin W G, Ji W J, Lan D, Wang Y R 2021 Acta Phys. Sin. 70 184701
Google Scholar
[25] Wodlei F, Sebilleau J, Magnaudet J, Pimienta1 V 2018 Nat. Commun. 9 820
Google Scholar
[26] Dipietro N D, Huh C, Cox R G 1978 J. Fluid Mech. 84 529
Google Scholar
[27] Girifalco L A 2000 J. Phys. Chem. B. 104 2599
Google Scholar
[28] Zhao G J, Pumera M 2012 J. Phys. Chem. B 116 10960
Google Scholar
[29] 杨宇平, 王农 2010 广东化工 37 180
Google Scholar
Yang Y P, Wang N 2010 Guangdong Huagong 37 180
Google Scholar
[30] Pin C, Souad H, Safouene O, Jesse S 2017 J. Phys. Chem. B 121 5824
Google Scholar
[31] Kim H, Boulogne F, Um E, Jacobi I, Button E, Stone H A 2016 Phys. Rev. Lett. 116 124501
Google Scholar
[32] Chandrasekhar S 1961 Hydrodynamic and Hydromagnetic Stability (Oxford University, New York/London) pp11–12
[33] Troian S M, Wu X L, Safran S A 1989 Phys. Rev. Lett. 62 1496
Google Scholar
[34] Afsar-Siddiqui A B, Luckham P F, Matar O K 2003 Langmuir 19 703
Google Scholar
[35] Hamraoui A, Cachile M, Poulard M, Cazabat A 2004 Colloid Surf. A 250 215
Google Scholar
[36] Sultan E, Boudaoud A, Ben Amar M 2005 J. Fluid Mech. 543 183
Google Scholar
[37] Gotkis Y, Ivanov I, Murisic N, Kondic L 2006 Phys. Rev. Lett. 97 186101
Google Scholar
[38] Bates C M, Stevens F, Langford S C, Dickinson J T 2008 Langmuir 24 7193
Google Scholar
[39] Plateau J A F 1873 Statique Expérimentale et Théorique des Liquides Soumis Aux Seules Forces Moléculaires(Vol. 2)(Paris: Gauthier-Villars) pp119–121
[40] Drazin P G, Reid W H 2004 Hydrodynamic Stability (2nd Ed.) (Cambridge: Cambridge University Press) pp432–433
[41] Liang X, Deng D S, Nave J C, Johnson, Steven G 2011 Phys. Fluids. 683 235
Google Scholar
[42] Demmel J W, Kagstrom B 1987 Linear Algebr. Appl. 88gebr 139
Google Scholar
[43] Tomotika S 1935 Proc. R. Soc. Lond. (A) 150 322
Google Scholar
[44] Chauhan A, Maldarelli C, Papageorgiou D T, Rumschitzki D S 2000 J. Fluid Mech. 420 120
Google Scholar
[45] Rayleigh L 1879 Proc. R. Soc. Lond. 29 71
Google Scholar
[46] Rayleigh L 1892 Phil. Mag. 34 145
Google Scholar
[47] Eggers J 1993 Phys. Rev. Lett 71 3458
Google Scholar
[48] 郝子洋, 杜凤沛 2008 大学化学 23 34
Google Scholar
Hao Z Y, Du F P 2008 Univ. Chem. 23 34
Google Scholar
[49] 甘泉, 杜源, 雷航, 阎晓琦 2016 大学化学 31 97
Google Scholar
Gan Q, Du Y, Lei H, Yan X Q 2016 Univ. Chem. 31 97
Google Scholar
[50] Deegan R D, Bakajin O, Dupont T F, Huber G, Nagel S R, Witten T A 1997 Nature 389 827
Google Scholar
[51] 王子昂, 郭航, 荣欣, 董桂芳 2019 物理化学学报 35 1259
Google Scholar
Wang Z A, Guo H, Rong X, Dong G F 2019 Acta Phys. Chim. Sin. 35 1259
Google Scholar
[52] 刘丹丹 2015 硕士学位论文 (杭州: 浙江大学)
Liu D D 2015 M. S. Thesis (Hangzhou: Zhejiang University
-
图 2 指状液柱碎裂过程的实验图像
Fig. 2. Experimental images of finger shaped liquid column fragmentation process.
图 4 振动模式示意图 (a) $ {\sigma }^{+}\left(k\right) $模式; (b) $ {\sigma }^{-}\left(k\right) $模式
Fig. 4. Schematic diagram of vibration mode: (a) $ {\sigma }^{+}\left(k\right) $ mode; (b) $ {\sigma }^{-}\left(k\right) $ mode.
图 5 (a) $ {\sigma }^{+}\left(k\right) $模式下增长率与波数和黏度比的关系; (b) 黏度比和最大增长率所对应的波数的关系
Fig. 5. (a) Relation of growth rate to wavenumber and viscosity ratio at $ {\sigma }^{+}\left(k\right) $ mode; (b) relationship between the viscosity ratio and the wave number corresponding to the maximum growth rate.
图 6 $ {\sigma }^{-}\left(k\right) $模式下增长率与波数的关系
Fig. 6. Relation of growth rate to wavenumber and viscosity ratio at $ {\sigma }^{-}\left(k\right) $ mode.
图 7 不同黏度比下两种模式最大增长率对应的波数的区间
Fig. 7. Interval of the wavenumber corresponding to the maximum growth rate of the two modes at different viscosity ratios.
图 8 不同醇溶液是否发生爆裂现象的体积分数统计数据
Fig. 8. Statistical data on volume fractions of several alcohol solutions for whether bursting phenomena occur.
图 9 花生油, 蓖麻油为液体B时, 乙醇溶液是否发生爆裂现象的体积分数统计数据
Fig. 9. Statistical data of volume fraction of ethanol solution with peanut oil and castor oil as liquid B.
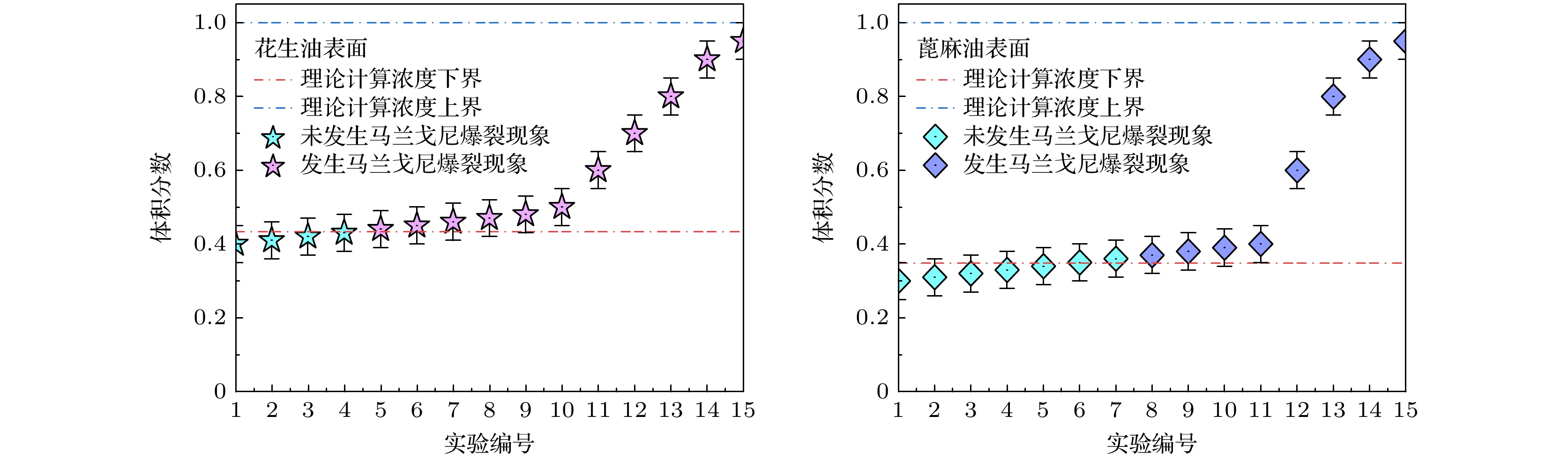
表 2 花生油, 蓖麻油为液体B时, 乙醇溶液发生爆裂现象的理论浓度范围与实验浓度范围
Table 2. Theoretical concentration range and experimental concentration range of ethanol solution when peanut oil and castor oil are liquid layers B.
液体层(厚度均为4 mm) 花生油 蓖麻油 表面张力/(N·m–1) 0.03302 0.03550 C的计算值/(mol·L–1) (7.38, 17.039) (5.925, 17.039) C的实验值/(mol·L–1) (7.67, 17.039) (6.305, 17.039) 绝对误差 0.29 0.38 相对误差 0.039 0.064 
下载: 导出CSV
表 1 不同醇溶液发生爆裂现象的理论浓度范围与实验浓度范围
Table 1. Theoretical concentration range and experimental concentration range of burst phenomena in several alcohol solutions.
二元混合物 乙醇 正丙醇 异丙醇 正丁醇 K 0.52241 0.19622 0.11931 0.07004 b 0.20449 0.22024 0.16302 0.23663 相关系数 0.99757 0.99980 0.99908 0.99620 C的计算值/(mol·L–1) (7.381, 7.039) (2.248, 13.37) (3.484, 13.06) (0.6627, 4.7237) C的实验值/(mol·L–1) (7.67, 17.039) (2.542, 13.37) (3.92, 13.06) (0.87, 4.37) 绝对误差 0.29 0.294 0.436 0.2073/–0.3537 相对误差 0.039 0.130 0.125 0.3128/–0.081
下载: 导出CSV
-
[1] Zhang J, Oron A, Behringer R P 2011 Phys. Fluids 23 072102
Google Scholar
[2] 赵子强, 韦伦存, 王浩, 张金宏, 钟运成, 卢希庭 1997 46 878
Google Scholar
Zhao Z Q, Wei L C, Wang H, Zhang J H, Zhong Y C, Lu X T 1997 Acta Phys. Sin. 46 878
Google Scholar
[3] 马书鹏, 林飞宇, 罗媛, 朱刘, 郭学益, 杨英 2022 71 158101
Google Scholar
Ma S P, Lin F Y, Luo Y, Zhu L, Guo X Y, Yang Y 2022 Acta Phys. Sin. 71 158101
Google Scholar
[4] Fay J A 1969 Oil on the Sea (Boston: Springer) pp53–63
[5] Huh C, Inoue M, Mason S G 1975 Can. J. Chem. Eng. 53 367
Google Scholar
[6] Foda M, Cox R G 1980 J. Fluid Mech. 101 33
Google Scholar
[7] Chaudhary K C, Redeopp L G 1980 Theory. J. Fluid Mech. 96 257
Google Scholar
[8] Chaudhary K C, Maxworthy T 1980 J. Fluid Mech. 96 275
Google Scholar
[9] Smith M K, Davis S H 1983 J. Fluid Mech. 132 119
Google Scholar
[10] Smith M K, Davis S H 1983 J. Fluid Mech. 132 145
Google Scholar
[11] Fanton X, Cazabat A M 1998 Langmuir 14 2554
Google Scholar
[12] Dussaud A D, Trojan S T 1998 Phys. Fluids 10 23
Google Scholar
[13] Borgas M S, Grotberg J B 1988 J. Fluid Mech. 188 151
Google Scholar
[14] Santiago Rosanne M, Vignes Adler M, Velarde M G 1997 J. Colloid. Interface Sci. 191 651
Google Scholar
[15] Vuilleumier R, Ego V, Neltner L, Cazabat A M 1995 Langmuir 11 4117
Google Scholar
[16] Kataoka D E, Troian S M 1997 J. Colloid. Nterf. Sci. 192 350
Google Scholar
[17] Jensen O E 1995 J. Fluid Mech. 293 349
Google Scholar
[18] Berg S 2009 Phys. Fluids 21 032105
Google Scholar
[19] Yamamoto D, Nakajima C, Shioi A, Krafft M P, Yoshikawa K 2015 Nat. Commun. 6 7189
Google Scholar
[20] Eggers J, Villermaux E 2008 Rep. Prog. Phys. 71 036601
Google Scholar
[21] Keiser L, Bense H, Colinet P, Bico J, Reyssat E 2017 Phys. Rev. Lett. 118 074504
Google Scholar
[22] Hamraoui A, Cachile M, Poulard C, Cazabat A M 2004 Colloid Surf. A Physicochem. Eng. Asp. 250 215
Google Scholar
[23] Hernández-Sánchez J F, Eddi A, Snoeijer J H 2015 Phys. Fluids 27 032003
Google Scholar
[24] 赵文景, 王进, 秦威广, 纪文杰, 蓝鼎, 王育人 2021 70 184701
Google Scholar
Zhao W J, Wang J, Qin W G, Ji W J, Lan D, Wang Y R 2021 Acta Phys. Sin. 70 184701
Google Scholar
[25] Wodlei F, Sebilleau J, Magnaudet J, Pimienta1 V 2018 Nat. Commun. 9 820
Google Scholar
[26] Dipietro N D, Huh C, Cox R G 1978 J. Fluid Mech. 84 529
Google Scholar
[27] Girifalco L A 2000 J. Phys. Chem. B. 104 2599
Google Scholar
[28] Zhao G J, Pumera M 2012 J. Phys. Chem. B 116 10960
Google Scholar
[29] 杨宇平, 王农 2010 广东化工 37 180
Google Scholar
Yang Y P, Wang N 2010 Guangdong Huagong 37 180
Google Scholar
[30] Pin C, Souad H, Safouene O, Jesse S 2017 J. Phys. Chem. B 121 5824
Google Scholar
[31] Kim H, Boulogne F, Um E, Jacobi I, Button E, Stone H A 2016 Phys. Rev. Lett. 116 124501
Google Scholar
[32] Chandrasekhar S 1961 Hydrodynamic and Hydromagnetic Stability (Oxford University, New York/London) pp11–12
[33] Troian S M, Wu X L, Safran S A 1989 Phys. Rev. Lett. 62 1496
Google Scholar
[34] Afsar-Siddiqui A B, Luckham P F, Matar O K 2003 Langmuir 19 703
Google Scholar
[35] Hamraoui A, Cachile M, Poulard M, Cazabat A 2004 Colloid Surf. A 250 215
Google Scholar
[36] Sultan E, Boudaoud A, Ben Amar M 2005 J. Fluid Mech. 543 183
Google Scholar
[37] Gotkis Y, Ivanov I, Murisic N, Kondic L 2006 Phys. Rev. Lett. 97 186101
Google Scholar
[38] Bates C M, Stevens F, Langford S C, Dickinson J T 2008 Langmuir 24 7193
Google Scholar
[39] Plateau J A F 1873 Statique Expérimentale et Théorique des Liquides Soumis Aux Seules Forces Moléculaires(Vol. 2)(Paris: Gauthier-Villars) pp119–121
[40] Drazin P G, Reid W H 2004 Hydrodynamic Stability (2nd Ed.) (Cambridge: Cambridge University Press) pp432–433
[41] Liang X, Deng D S, Nave J C, Johnson, Steven G 2011 Phys. Fluids. 683 235
Google Scholar
[42] Demmel J W, Kagstrom B 1987 Linear Algebr. Appl. 88gebr 139
Google Scholar
[43] Tomotika S 1935 Proc. R. Soc. Lond. (A) 150 322
Google Scholar
[44] Chauhan A, Maldarelli C, Papageorgiou D T, Rumschitzki D S 2000 J. Fluid Mech. 420 120
Google Scholar
[45] Rayleigh L 1879 Proc. R. Soc. Lond. 29 71
Google Scholar
[46] Rayleigh L 1892 Phil. Mag. 34 145
Google Scholar
[47] Eggers J 1993 Phys. Rev. Lett 71 3458
Google Scholar
[48] 郝子洋, 杜凤沛 2008 大学化学 23 34
Google Scholar
Hao Z Y, Du F P 2008 Univ. Chem. 23 34
Google Scholar
[49] 甘泉, 杜源, 雷航, 阎晓琦 2016 大学化学 31 97
Google Scholar
Gan Q, Du Y, Lei H, Yan X Q 2016 Univ. Chem. 31 97
Google Scholar
[50] Deegan R D, Bakajin O, Dupont T F, Huber G, Nagel S R, Witten T A 1997 Nature 389 827
Google Scholar
[51] 王子昂, 郭航, 荣欣, 董桂芳 2019 物理化学学报 35 1259
Google Scholar
Wang Z A, Guo H, Rong X, Dong G F 2019 Acta Phys. Chim. Sin. 35 1259
Google Scholar
[52] 刘丹丹 2015 硕士学位论文 (杭州: 浙江大学)
Liu D D 2015 M. S. Thesis (Hangzhou: Zhejiang University
下载:
计量
- 文章访问数: 1919
- PDF下载量: 85
- 被引次数: 0
