基于决策树方法的奇<i>A</i>核基态自旋预测

温湖峰; 尚天帅; 李剑; 牛中明; 杨东; 薛永和; 李想; 黄小龙

doi:10.7498/aps.72.20230530

摘要

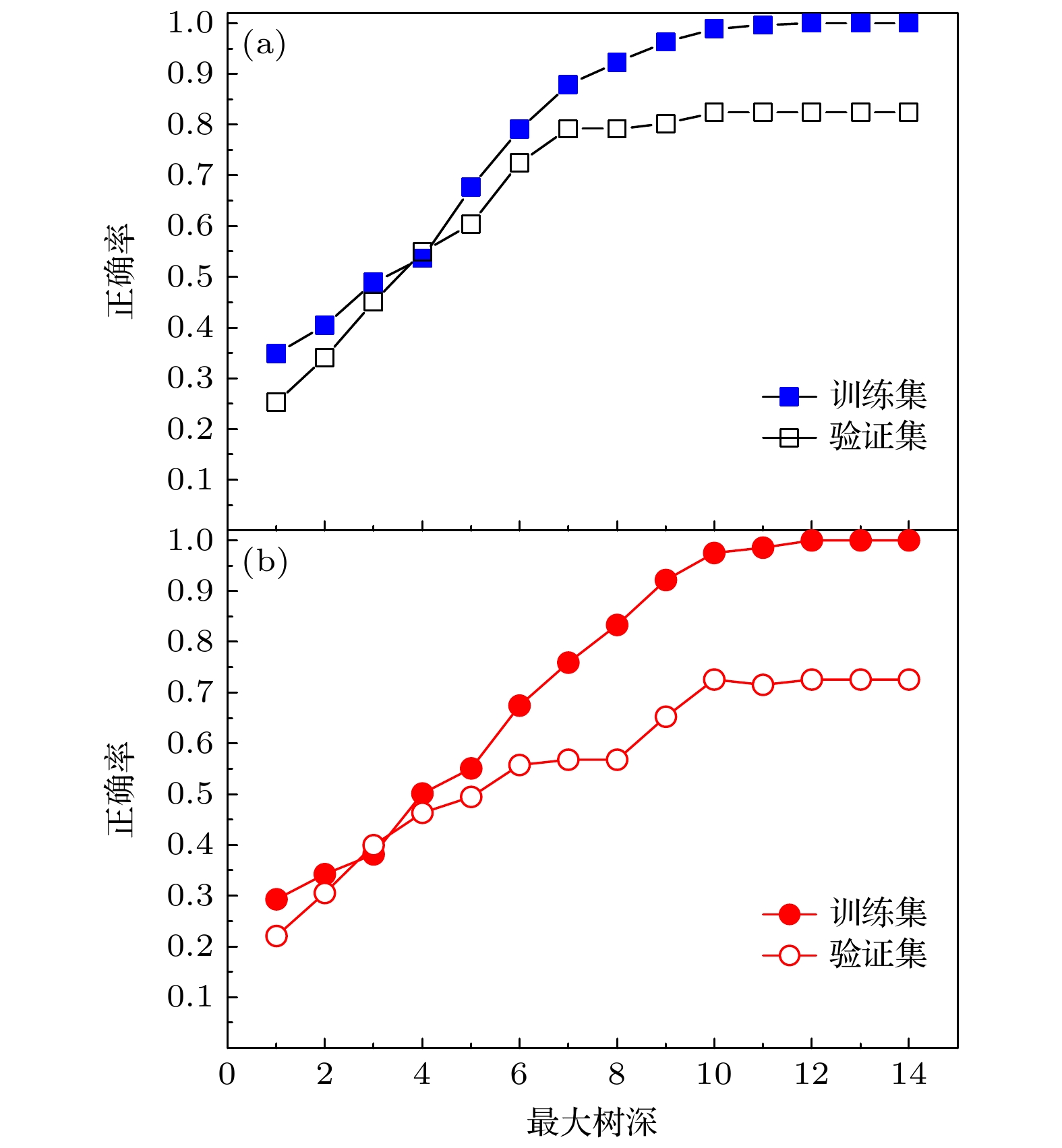
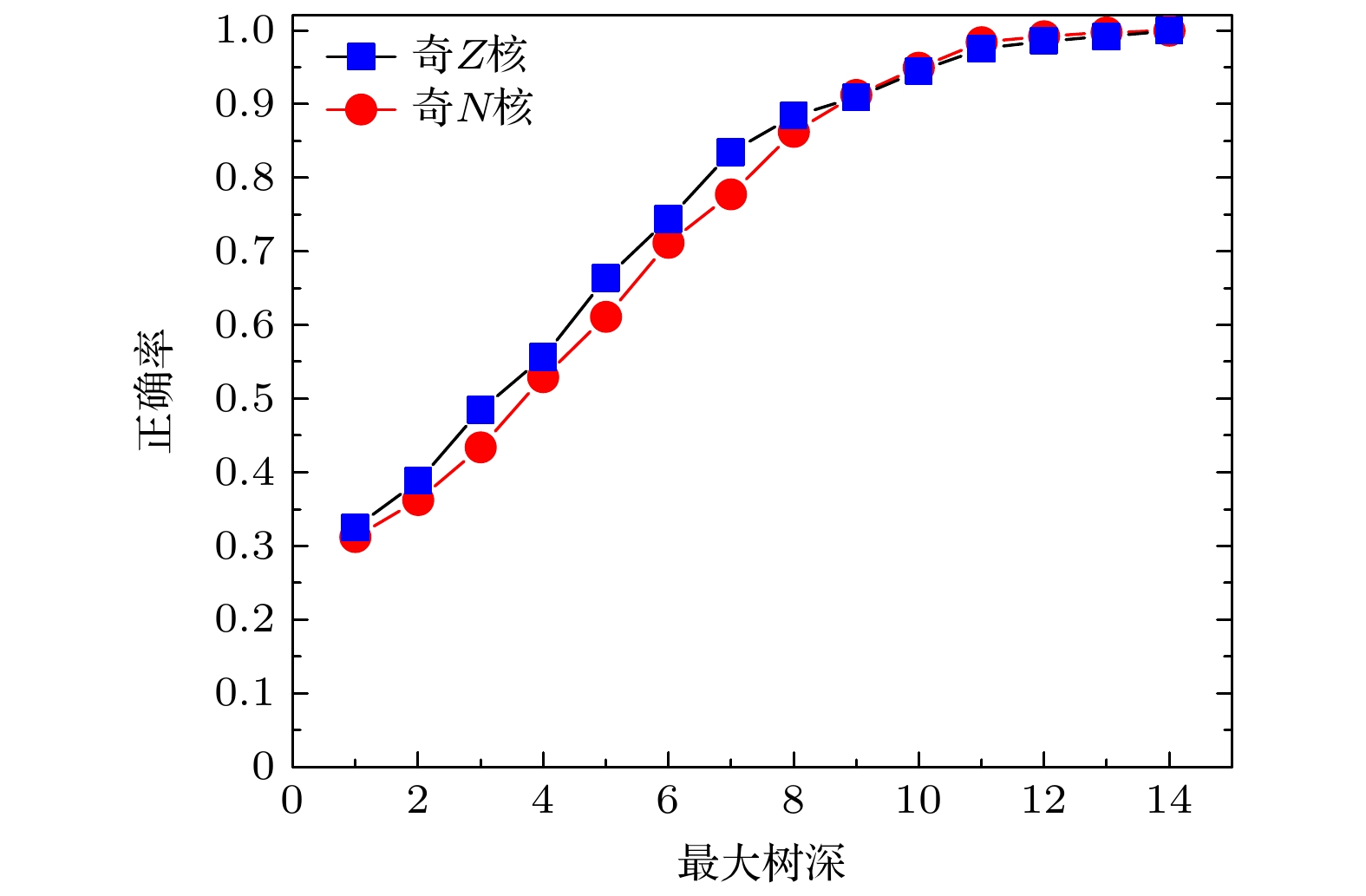
作为原子核的基本性质, 基态自旋一直是原子核数据与核结构基础研究领域的热点. 本文采用决策树方法对核素图上的奇质量数原子核(奇A核), 包括奇质子数原子核(奇Z核)与奇中子数原子核(奇N核), 进行了深入的研究, 并分别训练了奇Z核与奇N核的基态自旋预测模型. 其中在以75%∶25%的比例随机划分训练集与验证集的情况下, 奇Z核的训练集和验证集的正确率分别达到98.9%和79.3%; 奇N核的训练集和验证集的正确率分别达到98.6%和71.6%. 同时, 通过1000次随机选择训练集和验证集进行重复验证, 得到的正确率的标准误差均小于5%, 进一步验证了决策树的可靠性和泛化性能; 另一方面, 决策树的正确率远高于核结构研究中常用的理论模型, 如Skyrme-Hartree-Fock-Bogoliubov (SHFB)理论、协变密度泛函理论(CDFT)、有限程液滴模型等. 接下来, 以所有自旋确定的奇Z核和奇N核为学习集, 对共计254和268个自旋未确定但有推荐值的奇Z核和奇N核的基态自旋值进行了预测, 预测集符合率分别达到68.5%和69.0%. 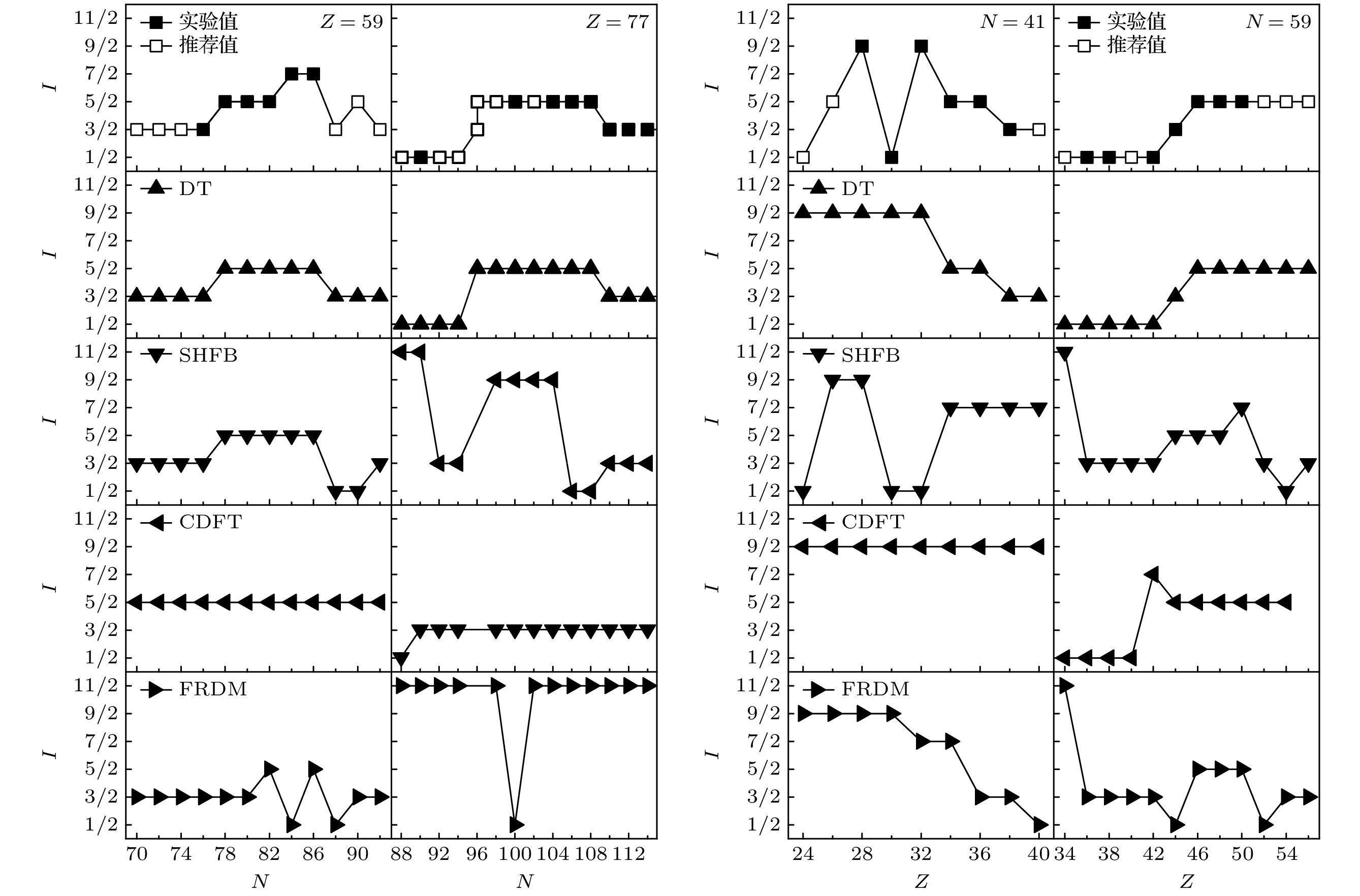最后, 选择$Z=59$, $Z=77$, $N=41$以及$N=59$四条奇质量数链, 讨论了决策树的学习(预测)结果与相应原子核的实验(推荐)值, 以及3种理论模型所给出结果的异同, 进一步展示了决策树在原子核基态自旋方面的研究与应用价值.

关键词:

基态自旋 /
奇A核 /
机器学习 /
决策树

Abstract

Ground-state spin, as a fundamental parameter of nucleus, has consistently been a hot topic in research on nuclear data and structure. In this paper, we extensively investigate the odd-mass nuclei (odd-A nuclei) on the nuclide chart by using decision trees, including odd-proton nuclei (odd-Z nuclei) and odd-neutron nuclei (odd-N nuclei), and train ground-state spin prediction models of odd-Z nuclei and odd-N nuclei. In the case of randomly dividing the training set and validation set in a ratio of 75% to 25%, the accuracy rate of the training set and validation set for odd-Z nuclei reach 98.9% and 79.3%, respectively. The accuracy rate of the training set and validation set for the odd-N nuclei reach 98.6% and 71.6%, respectively. At the same time, by 1000 random selections of training set and validation set, after being validated repetitively, the standard error of the accuracy rate obtained can be less than 5%, further verifying the reliability and generalization performance of the decision tree. On the other hand, the accuracy rate of decision tree is much higher than those of theoretical models commonly used in nuclear structure research, such as Skyrme-Hartree-Fock-Bogoliubov, covariant density functional theory, and finite range droplet model. Next, by taking all spin-determined odd-Z nuclei and odd-N nuclei as a learning set, the ground-state spin values for 254 spin undetermined but recommended odd-Z nuclei and 268 spin undetermined but recommended odd-N nuclei are predicted, with the predicted set coincidence rates reaching 68.5% and 69.0%, respectively. Finally, four odd-mass number chains, i.e. Z = 59, Z =77, N = 41, and N = 59, are selected to compare the learning (prediction) results of the decision tree with the experimental (recommended) values of the corresponding nuclei, and to discuss the differences and similarities in the results given by the three theoretical models, thereby further demonstrating the research and application value of the decision tree in the ground-state spin of nuclei.

Keywords:

作者及机构信息

1.
吉林大学物理学院, 长春　130012

2.
安徽大学物理与光电工程学院, 合肥　230601

3.
中国原子能科学研究院, 核数据重点实验室, 北京　102413

通信作者: 李剑, jianli@jlu.edu.cn ; 杨东, dyang@jlu.edu.cn ;

基金项目: 吉林省自然科学基金(批准号: 20220101017JC)、国家自然科学基金(批准号: 11675063, 11875070, 11935001)、核数据重点实验室(批准号: JCKY2020201C157)和安徽省项目(批准号: Z010118169)资助的课题

Authors and contacts

1.
School of Physics, Jilin University, Changchun 130012, China

2.
School of Physics and Optoelectronic Engineering, Anhui University, Hefei 230601, China

3.
Key Laboratory of Nuclear Data, Chinese Academy of Atomic Energy Sciences, Beijing 102413, China

Corresponding author: Li Jian, jianli@jlu.edu.cn ; Yang Dong, dyang@jlu.edu.cn ;

Funds: Project supported by the Natural Science Foundation of Jilin Province, China (Grant No. 20220101017JC), the National Natural Science Foundation of China (Grant Nos. 11675063, 11875070, 11935001), the Key Laboratory of Nuclear Data Foundation, China (Grant No. JCKY2020201C157), and the Anhui Project, China (Grant No. Z010118169)

文章全文 : translate this paragraph

参考文献

[1]	Yordanov D T, Kowalska M, Blaum K, Rydt M D, Flanagan K T, Lievens P, Neugart R, Neyens G, Stroke H H 2007 Phys. Rev. Lett. 99 212501 Google Scholar
[2]	Smirnova N, Bally B, Heyde K, Nowacki F, Sieja K 2010 Phys. Lett. B 686 109 Google Scholar
[3]	baglin C M 2012 Nucl. Data Sheets 113 2187 Google Scholar
[4]	Szuecs J, Johns M, Singh B 2004 Nucl. Data Sheets 102 1 Google Scholar
[5]	Singh B 2009 Nucl. Data Sheets 110 1 Google Scholar
[6]	Yang X F, Wang S J, Wilkins S G, Ruiz R F G 2023 Prog. Part. Nucl. Phys. 129 104005 Google Scholar
[7]	Carlson J A, Gandolfi S, Pederiva F, Pieper S C, Schiavilla R, Schmidt K E, Wiringa R B 2015 Rev. Mod. Phys. 87 1067 Google Scholar
[8]	Dickhoff W, Barbieri C 2004 Prog. Part. Nucl. Phys. 52 377 Google Scholar
[9]	Hagen G, Papenbrock T, Hjorth-Jensen M, Dean D J 2014 Rep. Prog. Phys. 77 096302 Google Scholar
[10]	Lee D 2009 Prog. Part. Nucl. Phys. 63 117 Google Scholar
[11]	Caurier E, Martínez-Pinedo G, Nowacki F, Poves A, Zuker A P 2005 Rev. Mod. Phys. 77 427 Google Scholar
[12]	Bender M, Heenen P H, Reinhard P G 2003 Rev. Mod. Phys. 75 121 Google Scholar
[13]	Ring P 1996 Prog. Part. Nucl. Phys. 37 193 Google Scholar
[14]	Meng J, Toki H, Zhou S G, Zhang S Q, Long W H, Geng L S 2006 Prog. Part. Nucl. Phys. 57 470 Google Scholar
[15]	Meng J 2016 Relativistic Density Functional for Nuclear Structure (Singapore: World Scientific) pp305–354
[16]	Shen S, Liang H, Long W H, Meng J, Ring P 2019 Prog. Part. Nucl. Phys. 109 103713 Google Scholar
[17]	Goriely S, Chamel N, Pearson J 2016 Phys. Rev. C 93 034337 Google Scholar
[18]	Xia X, Lim Y, Zhao P, et al. 2018 At. Data Nucl. Data Tables 121 1 Google Scholar
[19]	Möller P, Mumpower M R, Kawano T, Myers W D 2019 At. Data Nucl. Data Tables 125 1 Google Scholar
[20]	Benediktsson J, Swain P, Ersoy O 1990 IEEE Trans. Geosci. Remote Sens. 28 540 Google Scholar
[21]	Boehnlein A, Diefenthaler M, Sato N, Schram M, Ziegler V, Fanelli C, Hjorth-Jensen M, Horn T, Kuchera M P, Lee D, Nazarewicz W, Ostroumov P, Orginos K, Poon A, Wang X N, Scheinker A, Smith M S, Pang L G 2022 Rev. Mod. Phys. 94 031003 Google Scholar
[22]	Wu X H 2023 Front. Phys. 11 1061042 Google Scholar
[23]	Niu Z M, Liang H Z 2022 Phys. Rev. C 106 L021303 Google Scholar
[24]	Ming X C, Zhang H F, Xu R R, Sun X D, Tian Y, Ge Z G 2022 Nucl. Sci. Tech. 33 48 Google Scholar
[25]	Shou R, Yin X, Ma C, Lin M, Zhao Y 2022 Phys. Rev. C 106 L061304 Google Scholar
[26]	Gao Z P, Wang Y J, Lü H L, Li Q F, Shen C W, Liu L 2021 Nucl. Sci. Tech. 32 109 Google Scholar
[27]	Neufcourt L, Cao Y, Giuliani S, Nazarewicz W, Olsen E, Tarasov O B 2020 Phys. Rev. C 101 014319 Google Scholar
[28]	Neufcourt L, Cao Y, Nazarewicz W, et al. 2018 Phys. Rev. C 98 034318 Google Scholar
[29]	Rodríguez U B, Vargas C Z, Gonçalves M, Duarte S B, Guzmán F 2019 J. Phys. G: Nucl. Part. Phys. 46 115109 Google Scholar
[30]	Rodríguez U B, Vargas C Z, Gonçalves M, Duarte S B, Guzmán F 2019 Europhys. Lett. 127 42001 Google Scholar
[31]	Utama R, Piekarewicz J, Prosper H 2016 Phys. Rev. C 93 014311 Google Scholar
[32]	Bayram T, Akkoyun S, Kara S O 2014 Ann. Nucl. Energy 63 172 Google Scholar
[33]	Gazula S, Clark J, Bohr H 1992 Nucl. Phys. A 540 1 Google Scholar
[34]	Gernoth K, Clark J, Prater J, Bohr H 1993 Phys. Lett. B 300 1 Google Scholar
[35]	Niu Z, Liang H 2018 Phys. Lett. B 778 48 Google Scholar
[36]	Athanassopoulos S, Mavrommatis E, Gernoth K, Clark J W 2004 Nucl. Phys. A 743 222 Google Scholar
[37]	Clark J W, Li H 2006 Int. J. Mod. Phys. B 20 5015 Google Scholar
[38]	Niu Z M, Fang J Y, Niu Y F 2019 Phys. Rev. C 100 054311 Google Scholar
[39]	Dong X X, An R, Lu J X, Geng L S 2023 Phys. Lett. B 838 137726 Google Scholar
[40]	Dong X X, An R, Lu J X, Geng L S 2022 Phys. Rev. C 105 014308 Google Scholar
[41]	Ma J Q, Zhang Z H 2022 Chin. Phys. C 46 074105 Google Scholar
[42]	Ma Y, Su C, Liu J, Ren Z, Xu C, Gao Y 2020 Phys. Rev. C 101 014304 Google Scholar
[43]	Wu D, Bai C, Sagawa H, Zhang H 2020 Phys. Rev. C 102 054323 Google Scholar
[44]	Utama R, Chen W C, Piekarewicz J 2016 J. Phys. G: Nucl. Part. Phys. 43 114002 Google Scholar
[45]	Akkoyun S, Bayram T, Kara S O, Sinan A 2013 J. Phys. G: Nucl. Part. Phys. 40 055106 Google Scholar
[46]	Yuan Z, Tian D, Li J, Niu Z 2021 Chin. Phys. C 45 124107 Google Scholar
[47]	Clark J W, Gernoth K A, Dittmar S, Ristig M 1999 Phys. Rev. E 59 6161 Google Scholar
[48]	Gernoth K A, Clark J W 1995 Neural Networks 8 291 Google Scholar
[49]	Shang T S, Li J, Niu Z M 2022 Nucl. Sci. Tech. 33 153 Google Scholar
[50]	Yang Z X, Fan X H, Naito T, Niu Z, Li Z P, Liang H 2022 arXiv: 2205.15649[nucl-th]
[51]	Yang Z X, Fan X H, Yin P, Zuo W 2021 Phys. Lett. B 823 136650 Google Scholar
[52]	Costiris N, Mavrommatis E, Gernoth K A, Clark J W 2009 Phys. Rev. C 80 044332 Google Scholar
[53]	Wang Y, Zhang X, Niu Z, Li Z 2022 Phys. Lett. B 830 137154 Google Scholar
[54]	Akkoyun S, Kaya H, Torun Y 2022 Indian J. Phys. 96 1791 Google Scholar
[55]	Lasseri R D, Regnier D, Ebran J P, Penon A 2020 Phys. Rev. Lett. 124 162502 Google Scholar
[56]	Akkoyun S, Laouet N, Benrachi F 2020 arXiv: 2001.08561[nucl-th]
[57]	Ma N N, Zhao T L, Wang W X, Zhang H F 2023 Phys. Rev. C 107 014310 Google Scholar
[58]	Li C Q, Tong C N, Du H J, Pang L G 2022 Phys. Rev. C 105 064306 Google Scholar
[59]	Yuan Z, Bai D, Ren Z, Wang Z 2022 Chin. Phys. C 46 024101 Google Scholar
[60]	Kwon M, Oh Y, Song Y H, et al. 2021 New Physics: Sae Mulli 71 599 Google Scholar
[61]	Zhang X, Lin W, Yao J M, Jiao C F, Romero A M, Rodríguez T R, Hergert H 2023 Phys. Rev. C 107 024304 Google Scholar
[62]	Munoz J M, Akkoyun S, Reyes Z P, Pachon L A 2023 Phys. Rev. C 107 034308 Google Scholar
[63]	Niu Z, Liang H, Sun B, et al. 2019 Phys. Rev. C 99 064307 Google Scholar
[64]	Costiris N, Mavrommatis E, Gernoth K, Clark J, Li H 2008 arXiv: 0809.0383[nucl-th]
[65]	Akkoyun S, Amrani N, Bayram T 2023 Appl. Radiat. Isot. 191 110554 Google Scholar
[66]	Huang T X, Wu X H, Zhao P W 2022 Commun. Theor. Phys. 74 095302 Google Scholar
[67]	Ma C W, Wei X B, Chen X X, Peng D, Wang Y T, Pu J, Cheng K X, Guo Y F, Wei H L 2022 Chin. Phys. C 46 074104 Google Scholar
[68]	Peng D, Wei H L, Chen X X, Wei X B, Wang Y T, Pu J, Cheng K X, Ma C W 2022 J. Phys. G: Nucl. Part. Phys. 49 085102 Google Scholar
[69]	Ma C W, Peng D, Wei H L, Niu Z M, Wang Y T, Wada R 2020 Chin. Phys. C 44 014104 Google Scholar
[70]	Ma C W, Peng D, Wei H L, Wang Y T, Pu J 2020 Chin. Phys. C 44 124107 Google Scholar
[71]	Ma C W, Wei H L, Liu X Q, Su J, Zheng H, Lin W P, Zhang Y X 2021 Prog. Part. Nucl. Phys. 121 103911 Google Scholar
[72]	Yesilkanat C M, Akkoyun S 2023 J. Phys. G: Nucl. Part. Phys. 50 055101 Google Scholar
[73]	Akkoyun S, Bayram T 2014 Int. J. Mod. Phys. E 23 1450064 Google Scholar
[74]	Wang X, Zhu L, Su J 2021 Phys. Rev. C 104 034317 Google Scholar
[75]	Wu D, Bai C, Sagawa H, Nishimura S, Zhang H 2021 Phys. Rev. C 104 054303 Google Scholar
[76]	Wu X, Ren Z, Zhao P, et al. 2022 Phys. Rev. C 105 L031303 Google Scholar
[77]	Alhassan E, Rochman D, Vasiliev A, Hursin M, Koning A J, Ferroukhi H 2022 Nucl. Sci. Tech. 33 50 Google Scholar
[78]	Möller P, Nix J R 1990 Nucl. Phys. A 520 c369 Google Scholar
[79]	Breiman L 2001 Mach. Learn. 45 5 Google Scholar
[80]	Chen T, Guestrin C 2016 Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining San Francisco, USA, August 13–17, 2016 p785
[81]	Carnini M, Pastore A 2020 J. Phys. G: Nucl. Part. Phys. 47 082001 Google Scholar
[82]	Maderna C, Soardi P M 1985 Lezioni di analisi matematica (Torino: Città Studi Edizioni) pp1–354
[83]	Pedregosa F, Varoquaux G, Gramfort A, et al. 2011 J. Mach. Learn. Res. 12 2825 Google Scholar
[84]	From ENSDF database as of 5.16, 2019. Version available at http://www.nndc.bnl.gov/ensarchivals/[2019-5-16]
[85]	Wraith C, Yang X, Xie L, Babcock C, Bieroń J, Billowes J, Bissell M, Blaum K, Cheal B, Filippin L, Garcia Ruiz R, Gins W, Grob L, Gaigalas G, Godefroid M, Gorges C, Heylen H, Honma M, Jönsson P, Kaufmann S, Kowalska M, Krämer J, Malbrunot-Ettenauer S, Neugart R, Neyens G, Nörtershäuser W, Nowacki F, Otsuka T, Papuga J, Sánchez R, Tsunoda Y, Yordanov D 2017 Phys. Lett. B 771 385 Google Scholar

施引文献

图 1 奇A核基态自旋实验值分布, 用不同颜色表示不同自旋值　(a)奇Z核; (b)奇N核

Fig. 1. Experimental ground-state spin of odd-A nuclei: (a) Odd-Z nuclei; (b) odd-N nuclei. Different values are represented by different colors.

下载: 全尺寸图片幻灯片

图 2 训练集和验证集的正确率随最大树深的变化　(a)奇Z核; (b)奇N核

Fig. 2. Change of accuracy of training set and validation set with the maximum depth of decision tree: (a) Odd-Z nuclei; (b) odd-N nuclei

下载: 全尺寸图片幻灯片

图 3 学习集正确率随最大树深的变化

Fig. 3. Change of accuracy of learning set with the maximum depth of decision tree

下载: 全尺寸图片幻灯片

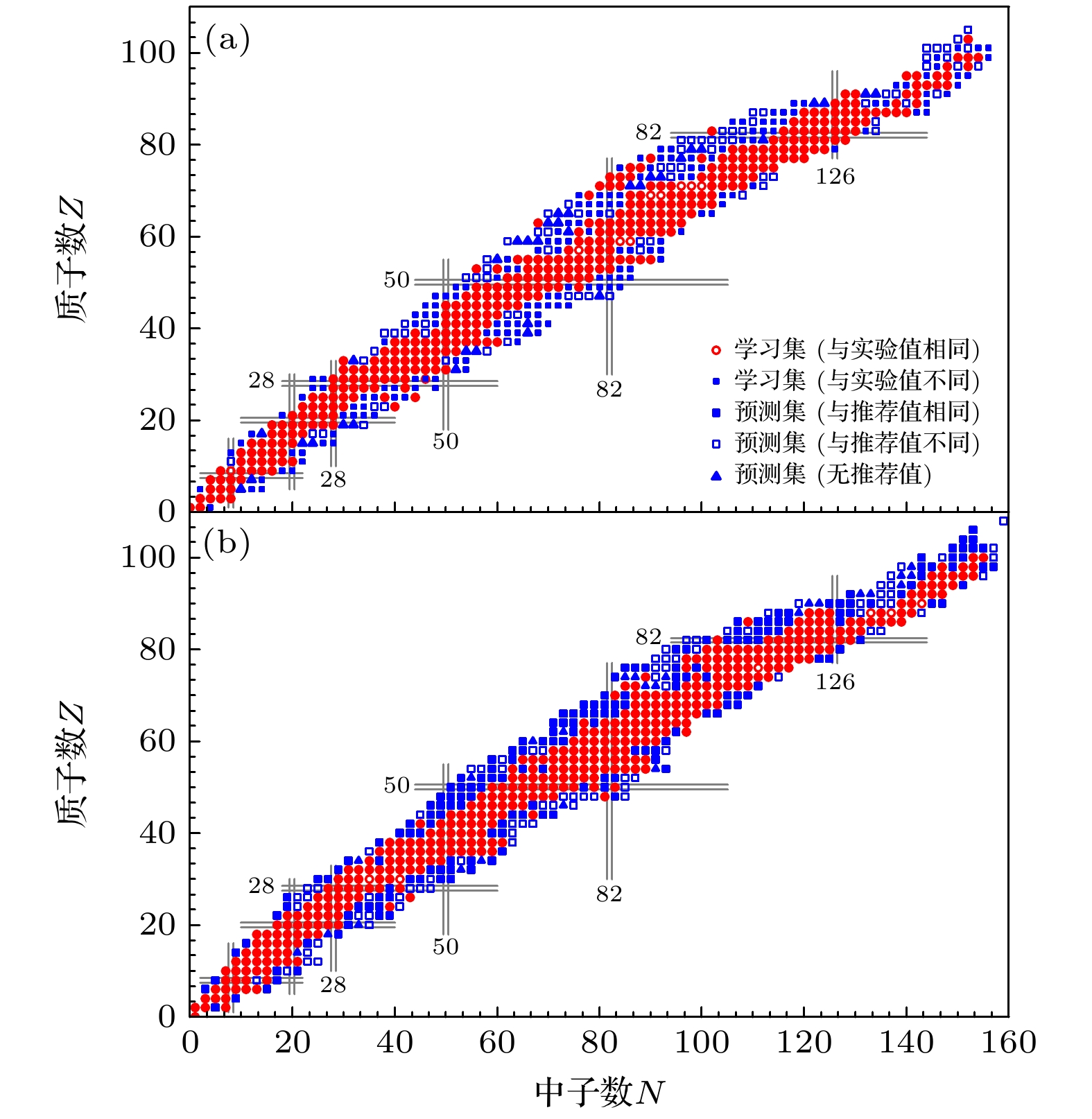
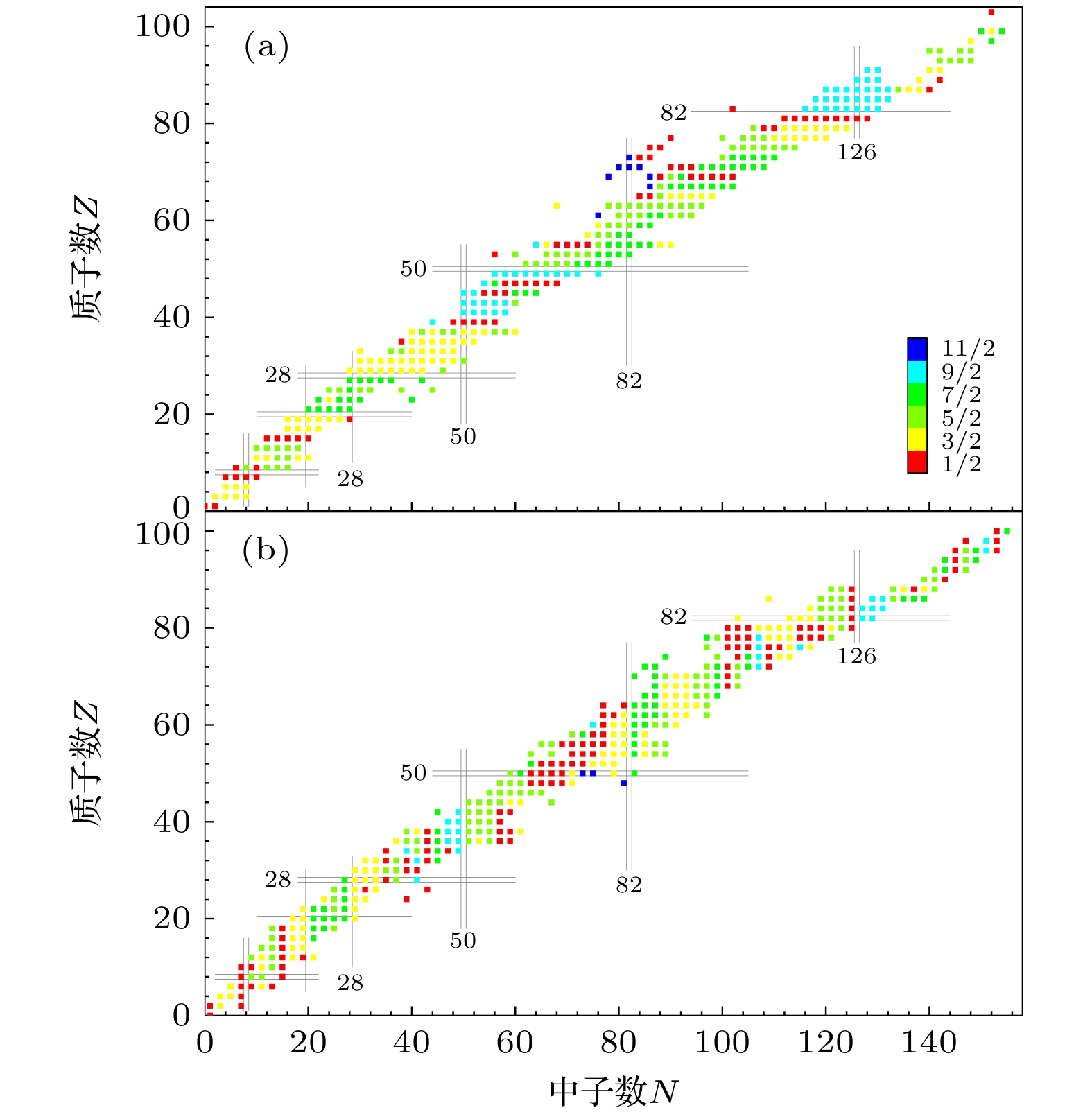
图 4 基于最大树深为11的决策树模型得到的原子核基态自旋学习集和预测集的结果, 其中与实验值相同(不同)的用红色实心(空心)圆圈表示; 与推荐值相同(不同)的用蓝色实心(空心)方块表示; 没有推荐值的用蓝色实心三角表示　(a)奇Z核; (b)奇N核

Fig. 4. Learning set and prediction set of the ground-state spin based on the decision tree model with the maximum depth of 11: (a) Odd-Z nuclei; (b) odd-N nuclei. The one same (different) as the experimental value is represented by a red solid (hollow) circle; the one same (different) as the recommended value is represented by blue solid (hollow) square; those with no recommended value are represented by blue solid triangles.

下载: 全尺寸图片幻灯片

图 5 基于决策树得到的质子数$ Z=59 $、$Z=77$的同位素链, 以及中子数$ N=41 $、$ N=59 $的同中异位素链原子核的基态自旋值, 并与SHFB、CDFT、FRDM预测结果和相应实验值、推荐值结果的比较

Fig. 5. The ground-state spin of $ Z=59 $ and $Z=77$ isotopic chains (left) and $ N=41 $ and $ N=59 $ isotonic chains (right) are obtained based on the decision tree, and compared with the predicted results of SHFB, CDFT, FRDM and the corresponding experimental and recommended values.

下载: 全尺寸图片幻灯片

表 1 最大树深为11时取1000次随机重复验证, 分别得到奇Z核和奇N核的训练集与验证集正确率平均值和正确率标准误差

Table 1. Average and standard error of the accuracy of the training set and the validation set obtained by 1000 random repetitions for odd-Z nuclei and odd-N nuclei, respectively

奇Z核奇N核

训练集验证集训练集验证集

平均值 97.6% 72.3% 96.5% 67.1%

标准误差 1.7% 4.5% 2.4% 4.9%

下载: 导出CSV

map

[1]	Yordanov D T, Kowalska M, Blaum K, Rydt M D, Flanagan K T, Lievens P, Neugart R, Neyens G, Stroke H H 2007 Phys. Rev. Lett. 99 212501 Google Scholar
[2]	Smirnova N, Bally B, Heyde K, Nowacki F, Sieja K 2010 Phys. Lett. B 686 109 Google Scholar
[3]	baglin C M 2012 Nucl. Data Sheets 113 2187 Google Scholar
[4]	Szuecs J, Johns M, Singh B 2004 Nucl. Data Sheets 102 1 Google Scholar
[5]	Singh B 2009 Nucl. Data Sheets 110 1 Google Scholar
[6]	Yang X F, Wang S J, Wilkins S G, Ruiz R F G 2023 Prog. Part. Nucl. Phys. 129 104005 Google Scholar
[7]	Carlson J A, Gandolfi S, Pederiva F, Pieper S C, Schiavilla R, Schmidt K E, Wiringa R B 2015 Rev. Mod. Phys. 87 1067 Google Scholar
[8]	Dickhoff W, Barbieri C 2004 Prog. Part. Nucl. Phys. 52 377 Google Scholar
[9]	Hagen G, Papenbrock T, Hjorth-Jensen M, Dean D J 2014 Rep. Prog. Phys. 77 096302 Google Scholar
[10]	Lee D 2009 Prog. Part. Nucl. Phys. 63 117 Google Scholar
[11]	Caurier E, Martínez-Pinedo G, Nowacki F, Poves A, Zuker A P 2005 Rev. Mod. Phys. 77 427 Google Scholar
[12]	Bender M, Heenen P H, Reinhard P G 2003 Rev. Mod. Phys. 75 121 Google Scholar
[13]	Ring P 1996 Prog. Part. Nucl. Phys. 37 193 Google Scholar
[14]	Meng J, Toki H, Zhou S G, Zhang S Q, Long W H, Geng L S 2006 Prog. Part. Nucl. Phys. 57 470 Google Scholar
[15]	Meng J 2016 Relativistic Density Functional for Nuclear Structure (Singapore: World Scientific) pp305–354
[16]	Shen S, Liang H, Long W H, Meng J, Ring P 2019 Prog. Part. Nucl. Phys. 109 103713 Google Scholar
[17]	Goriely S, Chamel N, Pearson J 2016 Phys. Rev. C 93 034337 Google Scholar
[18]	Xia X, Lim Y, Zhao P, et al. 2018 At. Data Nucl. Data Tables 121 1 Google Scholar
[19]	Möller P, Mumpower M R, Kawano T, Myers W D 2019 At. Data Nucl. Data Tables 125 1 Google Scholar
[20]	Benediktsson J, Swain P, Ersoy O 1990 IEEE Trans. Geosci. Remote Sens. 28 540 Google Scholar
[21]	Boehnlein A, Diefenthaler M, Sato N, Schram M, Ziegler V, Fanelli C, Hjorth-Jensen M, Horn T, Kuchera M P, Lee D, Nazarewicz W, Ostroumov P, Orginos K, Poon A, Wang X N, Scheinker A, Smith M S, Pang L G 2022 Rev. Mod. Phys. 94 031003 Google Scholar
[22]	Wu X H 2023 Front. Phys. 11 1061042 Google Scholar
[23]	Niu Z M, Liang H Z 2022 Phys. Rev. C 106 L021303 Google Scholar
[24]	Ming X C, Zhang H F, Xu R R, Sun X D, Tian Y, Ge Z G 2022 Nucl. Sci. Tech. 33 48 Google Scholar
[25]	Shou R, Yin X, Ma C, Lin M, Zhao Y 2022 Phys. Rev. C 106 L061304 Google Scholar
[26]	Gao Z P, Wang Y J, Lü H L, Li Q F, Shen C W, Liu L 2021 Nucl. Sci. Tech. 32 109 Google Scholar
[27]	Neufcourt L, Cao Y, Giuliani S, Nazarewicz W, Olsen E, Tarasov O B 2020 Phys. Rev. C 101 014319 Google Scholar
[28]	Neufcourt L, Cao Y, Nazarewicz W, et al. 2018 Phys. Rev. C 98 034318 Google Scholar
[29]	Rodríguez U B, Vargas C Z, Gonçalves M, Duarte S B, Guzmán F 2019 J. Phys. G: Nucl. Part. Phys. 46 115109 Google Scholar
[30]	Rodríguez U B, Vargas C Z, Gonçalves M, Duarte S B, Guzmán F 2019 Europhys. Lett. 127 42001 Google Scholar
[31]	Utama R, Piekarewicz J, Prosper H 2016 Phys. Rev. C 93 014311 Google Scholar
[32]	Bayram T, Akkoyun S, Kara S O 2014 Ann. Nucl. Energy 63 172 Google Scholar
[33]	Gazula S, Clark J, Bohr H 1992 Nucl. Phys. A 540 1 Google Scholar
[34]	Gernoth K, Clark J, Prater J, Bohr H 1993 Phys. Lett. B 300 1 Google Scholar
[35]	Niu Z, Liang H 2018 Phys. Lett. B 778 48 Google Scholar
[36]	Athanassopoulos S, Mavrommatis E, Gernoth K, Clark J W 2004 Nucl. Phys. A 743 222 Google Scholar
[37]	Clark J W, Li H 2006 Int. J. Mod. Phys. B 20 5015 Google Scholar
[38]	Niu Z M, Fang J Y, Niu Y F 2019 Phys. Rev. C 100 054311 Google Scholar
[39]	Dong X X, An R, Lu J X, Geng L S 2023 Phys. Lett. B 838 137726 Google Scholar
[40]	Dong X X, An R, Lu J X, Geng L S 2022 Phys. Rev. C 105 014308 Google Scholar
[41]	Ma J Q, Zhang Z H 2022 Chin. Phys. C 46 074105 Google Scholar
[42]	Ma Y, Su C, Liu J, Ren Z, Xu C, Gao Y 2020 Phys. Rev. C 101 014304 Google Scholar
[43]	Wu D, Bai C, Sagawa H, Zhang H 2020 Phys. Rev. C 102 054323 Google Scholar
[44]	Utama R, Chen W C, Piekarewicz J 2016 J. Phys. G: Nucl. Part. Phys. 43 114002 Google Scholar
[45]	Akkoyun S, Bayram T, Kara S O, Sinan A 2013 J. Phys. G: Nucl. Part. Phys. 40 055106 Google Scholar
[46]	Yuan Z, Tian D, Li J, Niu Z 2021 Chin. Phys. C 45 124107 Google Scholar
[47]	Clark J W, Gernoth K A, Dittmar S, Ristig M 1999 Phys. Rev. E 59 6161 Google Scholar
[48]	Gernoth K A, Clark J W 1995 Neural Networks 8 291 Google Scholar
[49]	Shang T S, Li J, Niu Z M 2022 Nucl. Sci. Tech. 33 153 Google Scholar
[50]	Yang Z X, Fan X H, Naito T, Niu Z, Li Z P, Liang H 2022 arXiv: 2205.15649[nucl-th]
[51]	Yang Z X, Fan X H, Yin P, Zuo W 2021 Phys. Lett. B 823 136650 Google Scholar
[52]	Costiris N, Mavrommatis E, Gernoth K A, Clark J W 2009 Phys. Rev. C 80 044332 Google Scholar
[53]	Wang Y, Zhang X, Niu Z, Li Z 2022 Phys. Lett. B 830 137154 Google Scholar
[54]	Akkoyun S, Kaya H, Torun Y 2022 Indian J. Phys. 96 1791 Google Scholar
[55]	Lasseri R D, Regnier D, Ebran J P, Penon A 2020 Phys. Rev. Lett. 124 162502 Google Scholar
[56]	Akkoyun S, Laouet N, Benrachi F 2020 arXiv: 2001.08561[nucl-th]
[57]	Ma N N, Zhao T L, Wang W X, Zhang H F 2023 Phys. Rev. C 107 014310 Google Scholar
[58]	Li C Q, Tong C N, Du H J, Pang L G 2022 Phys. Rev. C 105 064306 Google Scholar
[59]	Yuan Z, Bai D, Ren Z, Wang Z 2022 Chin. Phys. C 46 024101 Google Scholar
[60]	Kwon M, Oh Y, Song Y H, et al. 2021 New Physics: Sae Mulli 71 599 Google Scholar
[61]	Zhang X, Lin W, Yao J M, Jiao C F, Romero A M, Rodríguez T R, Hergert H 2023 Phys. Rev. C 107 024304 Google Scholar
[62]	Munoz J M, Akkoyun S, Reyes Z P, Pachon L A 2023 Phys. Rev. C 107 034308 Google Scholar
[63]	Niu Z, Liang H, Sun B, et al. 2019 Phys. Rev. C 99 064307 Google Scholar
[64]	Costiris N, Mavrommatis E, Gernoth K, Clark J, Li H 2008 arXiv: 0809.0383[nucl-th]
[65]	Akkoyun S, Amrani N, Bayram T 2023 Appl. Radiat. Isot. 191 110554 Google Scholar
[66]	Huang T X, Wu X H, Zhao P W 2022 Commun. Theor. Phys. 74 095302 Google Scholar
[67]	Ma C W, Wei X B, Chen X X, Peng D, Wang Y T, Pu J, Cheng K X, Guo Y F, Wei H L 2022 Chin. Phys. C 46 074104 Google Scholar
[68]	Peng D, Wei H L, Chen X X, Wei X B, Wang Y T, Pu J, Cheng K X, Ma C W 2022 J. Phys. G: Nucl. Part. Phys. 49 085102 Google Scholar
[69]	Ma C W, Peng D, Wei H L, Niu Z M, Wang Y T, Wada R 2020 Chin. Phys. C 44 014104 Google Scholar
[70]	Ma C W, Peng D, Wei H L, Wang Y T, Pu J 2020 Chin. Phys. C 44 124107 Google Scholar
[71]	Ma C W, Wei H L, Liu X Q, Su J, Zheng H, Lin W P, Zhang Y X 2021 Prog. Part. Nucl. Phys. 121 103911 Google Scholar
[72]	Yesilkanat C M, Akkoyun S 2023 J. Phys. G: Nucl. Part. Phys. 50 055101 Google Scholar
[73]	Akkoyun S, Bayram T 2014 Int. J. Mod. Phys. E 23 1450064 Google Scholar
[74]	Wang X, Zhu L, Su J 2021 Phys. Rev. C 104 034317 Google Scholar
[75]	Wu D, Bai C, Sagawa H, Nishimura S, Zhang H 2021 Phys. Rev. C 104 054303 Google Scholar
[76]	Wu X, Ren Z, Zhao P, et al. 2022 Phys. Rev. C 105 L031303 Google Scholar
[77]	Alhassan E, Rochman D, Vasiliev A, Hursin M, Koning A J, Ferroukhi H 2022 Nucl. Sci. Tech. 33 50 Google Scholar
[78]	Möller P, Nix J R 1990 Nucl. Phys. A 520 c369 Google Scholar
[79]	Breiman L 2001 Mach. Learn. 45 5 Google Scholar
[80]	Chen T, Guestrin C 2016 Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining San Francisco, USA, August 13–17, 2016 p785
[81]	Carnini M, Pastore A 2020 J. Phys. G: Nucl. Part. Phys. 47 082001 Google Scholar
[82]	Maderna C, Soardi P M 1985 Lezioni di analisi matematica (Torino: Città Studi Edizioni) pp1–354
[83]	Pedregosa F, Varoquaux G, Gramfort A, et al. 2011 J. Mach. Learn. Res. 12 2825 Google Scholar
[84]	From ENSDF database as of 5.16, 2019. Version available at http://www.nndc.bnl.gov/ensarchivals/[2019-5-16]
[85]	Wraith C, Yang X, Xie L, Babcock C, Bieroń J, Billowes J, Bissell M, Blaum K, Cheal B, Filippin L, Garcia Ruiz R, Gins W, Grob L, Gaigalas G, Godefroid M, Gorges C, Heylen H, Honma M, Jönsson P, Kaufmann S, Kowalska M, Krämer J, Malbrunot-Ettenauer S, Neugart R, Neyens G, Nörtershäuser W, Nowacki F, Otsuka T, Papuga J, Sánchez R, Tsunoda Y, Yordanov D 2017 Phys. Lett. B 771 385 Google Scholar

[1]	郭焱, 吕恒, 丁春玲, 袁晨智, 金锐博. 分数阶涡旋光衍射过程的机器学习识别. , 2025, 74(1): 014203. doi: 10.7498/aps.74.20241458
[2]	张童, 王加豪, 田帅, 孙旭冉, 李日. 基于机器学习的铸件凝固过程动态收缩行为. , 2025, 74(2): 028103. doi: 10.7498/aps.74.20241581
[3]	王鹏, 麦麦提尼亚孜·麦麦提阿卜杜拉. 机器学习的量子动力学. , 2025, 74(6): . doi: 10.7498/aps.74.20240999
[4]	邓祥文, 伍力源, 赵锐, 王嘉鸥, 赵丽娜. 机器学习在光电子能谱中的应用及展望. , 2024, 73(21): 210701. doi: 10.7498/aps.73.20240957
[5]	宋睿, 刘雪梅, 王海滨, 吕皓, 宋晓艳. 机器学习辅助的WC-Co硬质合金硬度预测. , 2024, 73(12): 126201. doi: 10.7498/aps.73.20240284
[6]	张桥, 谭薇, 宁勇祺, 聂国政, 蔡孟秋, 王俊年, 朱慧平, 赵宇清. 基于机器学习和第一性原理计算的Janus材料预测. , 2024, 73(23): 230201. doi: 10.7498/aps.73.20241278
[7]	张旭, 丁进敏, 侯晨阳, 赵一鸣, 刘鸿维, 梁生. 基于机器学习的激光匀光整形方法. , 2024, 73(16): 164205. doi: 10.7498/aps.73.20240747
[8]	张嘉晖. 蛋白质计算中的机器学习. , 2024, 73(6): 069301. doi: 10.7498/aps.73.20231618
[9]	张逸凡, 任卫, 王伟丽, 丁书剑, 李楠, 常亮, 周倩. 机器学习结合固溶强化模型预测高熵合金硬度. , 2023, 72(18): 180701. doi: 10.7498/aps.72.20230646
[10]	郭唯琛, 艾保全, 贺亮. 机器学习回归不确定性揭示自驱动活性粒子的群集相变. , 2023, 72(20): 200701. doi: 10.7498/aps.72.20230896
[11]	刘烨, 牛赫然, 李兵兵, 马欣华, 崔树旺. 机器学习在宇宙线粒子鉴别中的应用. , 2023, 72(14): 140202. doi: 10.7498/aps.72.20230334
[12]	管星悦, 黄恒焱, 彭华祺, 刘彦航, 李文飞, 王炜. 生物分子模拟中的机器学习方法. , 2023, 72(24): 248708. doi: 10.7498/aps.72.20231624
[13]	艾飞, 刘志兵, 张远涛. 结合机器学习的大气压介质阻挡放电数值模拟研究. , 2022, 71(24): 245201. doi: 10.7498/aps.71.20221555
[14]	康俊锋, 冯松江, 邹倩, 李艳杰, 丁瑞强, 钟权加. 基于机器学习的非线性局部Lyapunov向量集合预报订正. , 2022, 71(8): 080503. doi: 10.7498/aps.71.20212260
[15]	张嘉伟, 姚鸿博, 张远征, 蒋伟博, 吴永辉, 张亚菊, 敖天勇, 郑海务. 通过机器学习实现基于摩擦纳米发电机的自驱动智能传感及其应用. , 2022, 71(7): 078702. doi: 10.7498/aps.71.20211632
[16]	黎威, 龙连春, 刘静毅, 杨洋. 基于机器学习的无机磁性材料磁性基态分类与磁矩预测. , 2022, 71(6): 060202. doi: 10.7498/aps.71.20211625
[17]	林键, 叶梦, 朱家纬, 李晓鹏. 机器学习辅助绝热量子算法设计. , 2021, 70(14): 140306. doi: 10.7498/aps.70.20210831
[18]	陈江芷, 杨晨温, 任捷. 基于波动与扩散物理系统的机器学习. , 2021, 70(14): 144204. doi: 10.7498/aps.70.20210879
[19]	王伟, 揭泉林. 基于机器学习J₁-J₂反铁磁海森伯自旋链相变点的识别方法. , 2021, 70(23): 230701. doi: 10.7498/aps.70.20210711
[20]	杨自欣, 高章然, 孙晓帆, 蔡宏灵, 张凤鸣, 吴小山. 铅基钙钛矿铁电晶体高临界转变温度的机器学习研究. , 2019, 68(21): 210502. doi: 10.7498/aps.68.20190942

计量

文章访问数: 4206
PDF下载量: 99
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

基于决策树方法的奇A核基态自旋预测